Гриффитс Дж. Научные методы исследования осадочных пород

Подождите немного. Документ загружается.

342

ГЛАВА 1 г

Таблица 20.1

Источники изменчивости при пятифакторном анализе

Главные эффекты

Смешанный эффект первого порядка

Смешанный эффект второго порядка

Смешанный эффект третьего порядка

Смешанный эффект четвертого порядка

Сумма

Здесь потребуется 32 наблюдения всего лишь по одному наблюдению

на клетку; и если сделано q повторений, то для полностью сбалансированно-

го способа потребуется 32q наблюдения. Такое предвидение последствий при-

менения той или иной процедуры — одно из преимуществ научного метода

приближений.

Вернемся к трефакторной классификации. Общее количество наблю-

дений N = prcq, и структура эксперимента может быть записана в следую-

щем виде:

Xijhi = μ

-(-

щ +

β;

+ Ук + α

βο·

OCYifc

+ β Тд + а$Ут + +

mi);

t=l, ..., ρ; / = 1, ..., r;

= I, ..., с

q=l, ..., q, (20.1)

где α — влияние оператора, β — влияние рядов, у — влияние колонок,

δ — вклад, вносимый повторениями, который смешивается с другими источ-

никами изменчивости гцы- В табл. 20.2 приведена обобщенная схема соот-

Таблица 20.2

юбщающая таблица трехфакторниго дисперсионного анализа

(бесконечная совокупность—модель случайных эффектов)

Коли-

Источник Число степеней

Ожидаемый средний квадрат

чество

пунктов

изменчивости

свободы

Ожидаемый средний квадрат

Операторы р-1

I + I

Irc +

Ic +

Ir +

Ряды

г —1

I + I

Ire + P

Kc +

Ir +

QOf-

Колонки

с —1

I + I

Ire + PI

l с + P

Оператор

χ ряды (р-1) (г-1)

I + I

Irc+

Операторы χ ко-

(P-I) (е-1)

I +I

Irc +

лонки

I +I

Irc +

Ряды χ колонки

(

_1) (с_1)

I+ 1

%rc + PWf-c

Операторы X ря-

(р_1) (г-1) (с-1)

I +I

Ire

ды X колонки

I +I

Ire

Повторения (ошиб-

ка)

pre (? —1)

Сумма

prcq — 1

IOt

ветствующего дисперсионного анализа. Изучение оценок ожидаемых средних

квадратов покажет ошибки для проверки значимости вкладов в диспер-

сию на различных уровнях, т. е. если все взаимодействия равны нулю, глав-

ные эффекты могут быть проверены по ошибкам. Все прочие исходы приво-

дят к тем или иным усложнениям. Предположим, что взаимодействие второ-

ПРОЧИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕШЕНИЯ

343·

го порядка практически нулевое. Тогда каждое взаимодействие первого

порядка может быть проверено по ошибке. Если то или другое значительно,

то для одного из главных эффектов оно становится остаточным членом. Если

два взаимодействия первого порядка значительно более ошибки, то простого

критерия, по крайней мере для двух главных эффектов, не существует.

Поэтому, если известно, что влияние взаимодействий не равно нулю, при изу-

чении этих взаимодействий следует соблюдать осторожность; когда природа

и порядок значений изменчивости не известны заранее из проведенных экспе-

риментов, такой план изучения будет явно трудным для обработки. Добавим,

что все это относится к модели бесконечной совокупности; конечная и сме-

шанная модели, видимо, еще более сложны [27]. Сейчас в большинстве слу-

чаев при применении такого экспериментального решения в геологической

работе исследователь должен быть готов к повторению эксперимента, изме-

нению процедуры измерений и регулированию способа отбора еще до того,

как могут быть сделаны заключения.

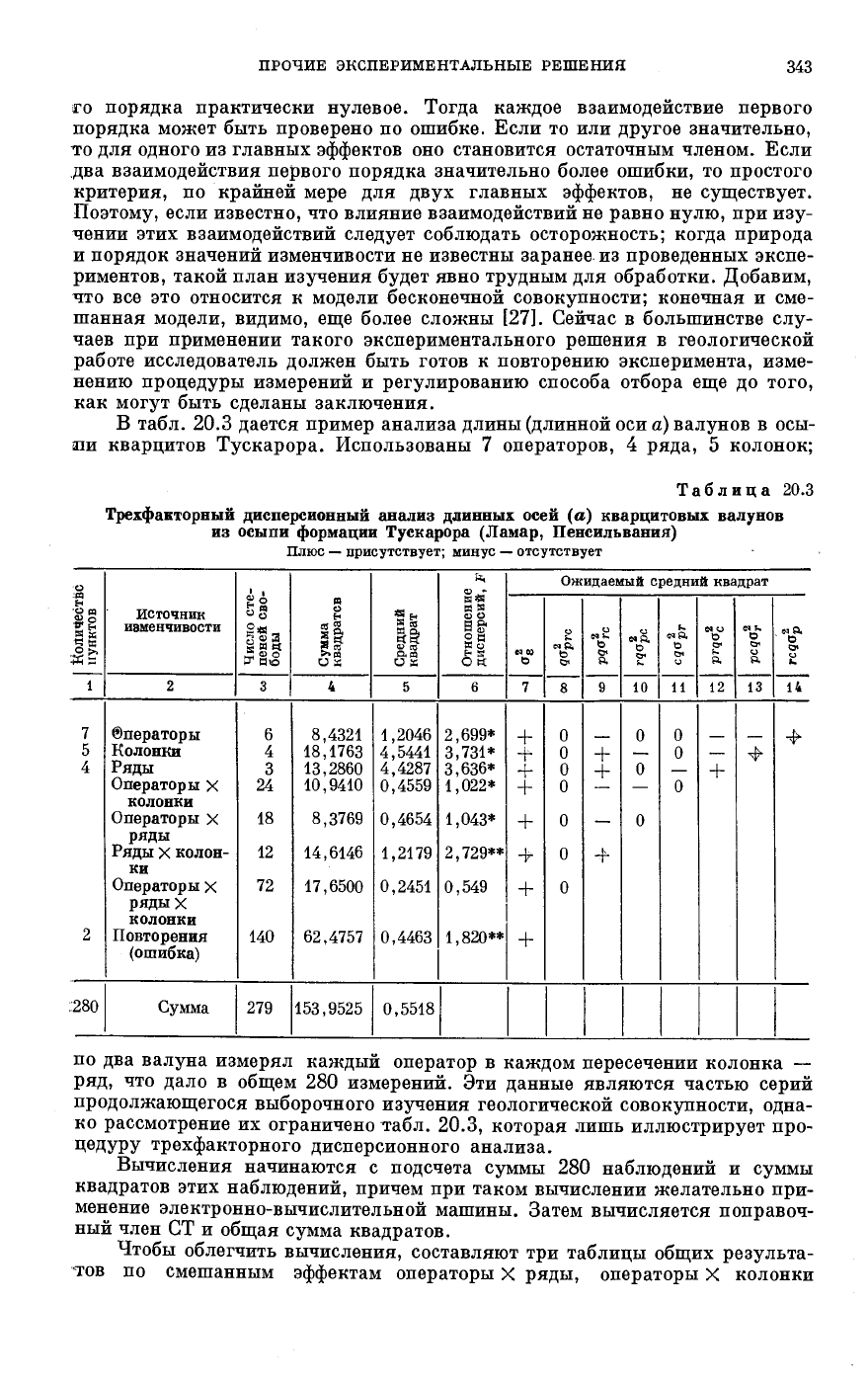
В табл. 20.3 дается пример анализа длины (длинной оси а) валунов в осы-

ии кварцитов Тускарора. Использованы 7 операторов, 4 ряда, 5 колонок;

Таблица 20.3

Трехфакторный дисперсионный анализ длинных осей (а) кварцитовых валунов

из осыпи формации Тускарора (Ламар, Пенсильвания)

Плюс — присутствует; минус

—

отсутствует

ь.

Ожидаемый средний квадрат

•о

s™

S и

S в

W =

Источник

изменчивости

в*,

Isa

.¾ ®

β S

j? re

S S

« я

О в

в«

И S

о о

Sg·

° а

П U

о*

м А

е>

о<

я»

<я Р.

СУ

м υ

ί.

еэ ϊ.

94 Р.

О»

I»

3 4

5 6

9 10 11

12 13 14

©ператоры

Колонки

Ряды

Операторы χ

колонки

Операторы X

ряды

Ряды χ колон-

ки

Операторы χ

ряды χ

колонки

Повторения

(ошибка)

8,4321

18,1763

13,2860

10,9410

8,3769

1,2046

4,5441

4,4287

0,4559

0,4654

2,699*

3,731*

3,636*

1,022*

1,043*

©ператоры

Колонки

Ряды

Операторы χ

колонки

Операторы X

ряды

Ряды χ колон-

ки

Операторы χ

ряды χ

колонки

Повторения

(ошибка)

140

14,6146

17,6500

62,4757

1,2179

0,2451

0,4463

2,729**

0,549

1,820**

:280

Сумма 279

153,9525 0,5518

по два валуна измерял каждый оператор в каждом пересечении колонка —

ряд, что дало в общем 280 измерений. Эти данные являются частью серий

продолжающегося выборочного изучения геологической совокупности, одна-

ко рассмотрение их ограничено табл. 20.3, которая лишь иллюстрирует про-

цедуру трехфакторного дисперсионного анализа.

Вычисления начинаются с подсчета суммы 280 наблюдений и суммы

квадратов этих наблюдений, причем при таком вычислении желательно при-

менение электронно-вычислительной машины. Затем вычисляется поправоч-

ный член CT и общая сумма квадратов.

Чтобы облегчить вычисления, составляют три таблицы общих результа-

тов по смешанным эффектам операторы X ряды, операторы X колонки

344

ГЛАВА 1 г

и ряды X колонки. По этим таблицам из соответствующих конечных резуль-

татов могут быть вычислены суммы квадратов по каждому главному эффек-

ту, данные по операторам, рядам и колонкам. Затем из общих результатов

в массиве каждой таблицы получают сумму квадратов для каждого взаимо-

действия первого порядка.

Теперь имеется четыре таблицы для каждого ряда итогов по смешанному

эффекту оператор X колонка, которые соответствуют взаимодействиям вто-

рого порядка — операторы X ряды X колонки. Остаточный член находят

по разности. Результаты этих вычислений даны в колонке 4 табл. 20.3. Сред-

ние квадраты (колонка 5) находят делением каждой суммы квадратов на соот-

ветствующее число степеней свободы (колонка 3).

Дисперсия (средний квадрат), связанная с полной суммой квадратов,

могла быть использована в качестве наилучшей несмещенной оценки гене-

ральной дисперсии, если все источники измерений оказались бы незначитель-

ными. Но если какой-либо другой источник изменчивости значителен, эта

оценка окажется смещенной.

Проверку гипотезы надо начинать с сравнения остаточного члена со

средними квадратами взаимодействия второго порядка в отношении дис-

персий F =

{а%

-f qa%

)lal, что даст F = 0,2451/0,4463 = 0,549, когда соот-

ветственные компоненты дисперсии используются в качестве оценок средних

квадратов. Гипотеза H

заключается в утверждении, что все 140 средних зна-

чений, полученных операторами по рядам и колонкам, представляют слу-

чайные выборки из одной и той же (нормальной) совокупности. Из этого сле-

дует, что если H

верна, то Op

= 0; из таблиц значения F [15] получаем:

— -^05,75,125

1)39. Так как F = 0,549, т. е. меньше табличного значения,

то гипотеза не отвергается и можно считать, что Op

= 0. Если дисперсион-

ное отношение является обратным данному, то критическое значение

F05, loo,

7о

= 1,45, а наблюдаемое значение F = 0,4463/0,2451 = 1,820; это

значительно больше, чем при 1-процентном уровне; очевидно, средние более

однородны, чем можно было бы ожидать при случайном опробовании одной

и той же (нормальной) совокупности. В некоторйх экспериментах это может

означать, что отбор не случаен, т. е. средние слишком схожи между собой.

В данном случае это отражает следующий факт: изменчивость длинных осей

внутри пар валунов значительно больше изменчивости между средними

из наборов по два; подобное явление подчеркивает значительную изменчи-

вость относительно неотсортированного материала (стадия 1) выборочной

модели (фиг. 2.3).

Так как величина Op

практически близка нулю, эти две оценки можно

рассматривать в качестве двух независимых оценок той же дисперсии и объе-

динять с целью оценки, основанной на 212 степенях свободы. Однако вслед-

ствие того, что средние небольших выборок значительно меньше средних

по отдельным валунам, представляется более реальным («геологичным»)

использовать данную погрешность для последующих проверок без объеди-

нения. Фактически в этом случае ни та ни другая процедура не окажет влия-

ния на заключения при проверке гипотезы.

Следующим шагом процедуры является сравнение каждого эффекта вза-

имодействия первого порядка с ошибкой. Взаимодействия операторы X

X ряды и взаимодействия операторы X колонки оказываются незначимыми,

в то время как взаимодействия ряды X колонки значимы при 1-процентном

уровне. В действительности же это означает, что величины Op

и о|

близки

нулю. При переходе от ряда к ряду или от колонки к колонке влияния опе-

раторов нет. Это подтверждается при контроле измерительной процедуры.

Значительное взаимодействие между рядами и колонками означает, что вели-

чина afc не равна нулю, и, следовательно, различия между средними по рядам

не постоянны по сравнению с колонками и наоборот. В случае значительной

ПРОЧИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕШЕНИЯ

345·

тенденции к изменениям размеров валунов, т. е. когда размеры валунов уве-

личиваются в направлении к основанию осыпи, взаимодействие должно быть

нулевым; градиент между средними по рядам сохраняется по длине каждой

колонки. G другой стороны, если по направлению от одной стороны осыпи

к другой наблюдается значительный градиент в размерах, различие между

данными по колонкам должно быть значительным, а взаимодействие — нуле-

вым. Когда эффект взаимодействия ряды X колонки значителен, «градиент»

оказывается непоследовательным, и выводимые значения, основанные

на сравнении главных эффектов и различий по рядам и колонкам,, становятся

сомнительными.

Так как эффекты взаимодействия первого и второго порядков равны нулю,

остаточный член для проверки различий между показаниями операторов

получается из различий между повторными замерами; при проверке соот-

ветствующей нулевой гипотезы Op = 0 эти различия между средними

показаниями операторов значимы при 5-процентном уровне. Иначе говоря,

гипотеза сГр = 0 отвергается, а показания операторов расходятся. Такое

положение обычно для подобных экспериментов; однако вследствие того,

что эффекты взаимодействий операторов равны нулю, эти различия ортого-

нальны по отношению к различиям между средними по колонкам и различи-

ям между средними по рядам и не оказывают существенного влияния на ре-

зультаты сравнения. Очень важно достигнуть подобного результата, потому

что при непоследовательных показаниях операторов и как следствие при

значительном взаимодействии операторов из таких данных нельзя вывести

общего заключения. Последнее означает, что, если данный эксперимент пов-

торили бы другие исследователи, у них получились бы иные результаты.

Вследствие того что эффект взаимодействия ряды X-колонки значите-

лен, т. е. afc φ O

соответствующий средний квадрат становится остаточным

членом для проверки главных эффектов этого взаимодействия. Гипотезы of =

= 0 и а? = 0 отвергаются как для рядов, так и для колонок, а различия меж-

ду средними по рядам (и колонкам) значительно превышают изменчивость,

вызванную эффектом взаимодействия ряды X колонки (при 5-процентном

уровне). Общей тенденции к изменению, однако, не возникает, так как зна-

чительное взаимодействие означает, что средние по некоторым колонкам пре-

вышают средние значения некоторых рядов; то же можно сказать и о разли-

чиях между средними по рядам. На практике теперь следовало бы построить,

график взаимодействия ряды X колонки и ввести значения средних по рядам

на каждую колонку и средние по колонкам на каждый ряд, чтобы можно было

исследовать природу этих различий. Аналогично можно было бы проконтро-

лировать измеренную длину осей а валунов (путем вычисления для сопостав-

лений доверительных пределов Шеффе с использованием дисперсии взаимо-

действия) и объяснить причину появления образцов любого размера.

Разумеется, эксперимент вначале касался лишь вопроса оценки ком-

понента дисперсии как основы для рекомендаций по дальнейшему опробо-

ванию, так что эти компоненты дисперсии должны были быть изолированы,

чтобы можно было исследовать величину влияния каждого источника

в отдельности.

20.3. ДРУГИЕ ПРИМЕРЫ

ТРЕХФАКТОРНОГО ДИСПЕРСИОННОГО АНАЛИЗА

Первым примером дисперсионного анализа в геологической литературе

является классификация по трем признакам (смешанная модель), с помощью

которой сравнивают различные методы просеивания [422]. Другой пример,

в котором показывается отрицательное влияние взаимодействия, касается

сравнения визуальных оценок сферичности и окатанности кварцевых зерен

пляжных песков [364]; отсутствие повторных замеров и относительно боль-

346

ГЛАВА 1 г

шое влияние взаимодействия второго порядка приводит к противоречивости

результатов.

Примеры классификации по четырем признакам и смешанных моделей

описаны Бенеттом и Франклином [27], а также Браунли [44]. Исследователь,

интересующийся применением подобных решений, должен использовать эти

примеры с соблюдением большой осторожности еще на стадии планирования

эксперимента.

20.4. ЛАТИНСКИЙ КВАДРАТ

Проведение эксперимента латинским квадратом — одна из форм трех-

факторного анализа, использующая объединение факторов для уменьшения

количества наблюдений. Например, структура полностью сбалансированной

классификации по трем признакам без повторений будет следующей:

Xt Jhi = μ + «ί +

β;

Tfe

+ сфц + a\ik + βγ# + (сфуш +

ε*

j м), (20.2)

где остаточный член содержит вклад от взаимодействия второго порядка

вместе с влиянием от всех неучтенных источников (e

fti

). Структура анало-

гичного эксперимента, производимого латинским квадратом, следующая:

·Χ"№

= μ + αί +

β^

ΪΛ

εο·Λ.

(20.3)

Можно заметить, что эффект от действия неучтенных источников измен-

чивости здесь объединяет все вклады в дисперсию от трех взаимодействий пер-

вого порядка и взаимодействия второго порядка. Значительное влияние

любого взаимодействия приводит к увеличению остаточного члена и понижает

чувствительность эксперимента; поскольку же мы не располагаем способом

проверки этих результатов, заключения в подобных случаях могут оказаться,

к сожалению, ошибочными.

План эксперимента латинским квадратом был разработан для весьма спе-

цифической цели — для полевых агрономических исследований. Главной

задачей при этом обычно является сравнение средних урожаев, обусловлен-

ных некоторыми переменными (или способами ухода, например примене-

нием различных удобрений). При этом ряды и колонки используются просто

в качестве двухфакторной стратификации для сокращения влияния гетеро-

генных изменений плодородия почвы по блокам, в которых высажены изу-

чаемые растения. И в этом случае не пытаются интерпретировать «расхож-

дения» между рядами или колонками; они фактически рассматриваются как

фиксированные результаты, и эксперимент соответствует модели 1 или модели

фиксированного типа [332]. Следует подчеркнуть, что выборочные правила

при агрономических экспериментах основываются на способах продолжи-

тельного отбора, называемых единообразными испытаниями. Этому испыта-

нию подвергались многие обычные растения, прежде чем данный способ был

окончательно разработан, и в результате выяснилось, что результат взаи-

модействий можно не принимать во внимание. В геологической практике

такое продолжительное изучение выборочных изменений пока еще не осу-

ществлялось, поэтому предположения об отсутствии эффектов взаимодейст-

вия могут привести

неверным результатам. Кроме того, латинским квадратом

не оценивают компоненты дисперсии, а лишь сравнивают средние зна-

чения; чтобы выделить это последнее, в данной модели используется обозна-

чение θ вместо дисперсий в колонке ожидаемых средних квадратов (табл. 20.4)

Положительная сторона латинского квадрата заключается в сильном

сокращении количества наблюдений, что бывает весьма кстати, когда необ-

ходимые данные уже собраны и исследователь считает, что это сокращение

пройдет без потерь. Например, если классификация по трем признакам про-

ведена без повторений и если каждый главный эффект представлен четырь-

мя классами, это значит, что имеется 4 X 4 X 4 = 64 наблюдения; в ана-

ПРОЧИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕШЕНИЯ 347·

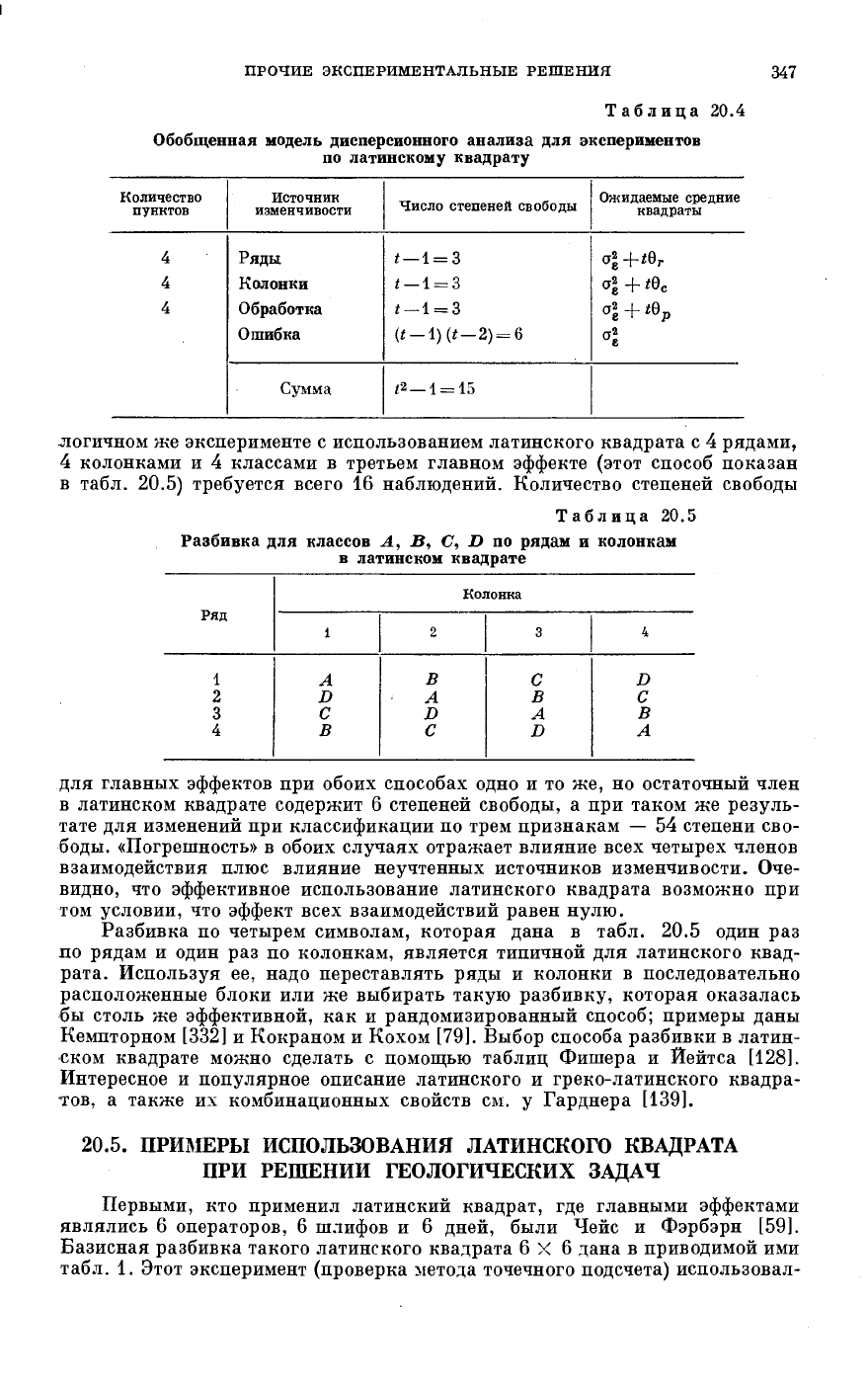
Таблица 20.4

Обобщенная модель дисперсионного анализа для экспериментов

по латинскому квадрату

Количество

пунктов

Источник

изменчивости

Число степеней свободы

Ожидаемые средние

квадраты

Ряды

Колонки

Обработка

Ошибка

—1

= 3

—1

= 3

г —1

= 3

(ί —1) (г—2) = 6

σ|+ίθ

σ| + г0

+ *θ

Сумма

«2 —

= 15

логичном же эксперименте с использованием латинского квадрата с 4 рядами,

4 колонками и 4 классами в третьем главном эффекте (этот способ показан

в табл. 20.5) требуется всего 16 наблюдений. Количество степеней свободы

Таблица 20.5

Разбивка для классов А, В, С, D по рядам и колонкам

в латинском квадрате

Ряд

Колонка

Ряд

1 Z

3 С

4 В С

для главных эффектов при обоих способах одно и то же, но остаточный член

в латинском квадрате содержит 6 степеней свободы, а при таком же резуль-

тате для изменений при классификации по трем признакам — 54 степени сво-

боды. «Погрешность» в обоих случаях отражает влияние всех четырех членов

взаимодействия плюс влияние неучтенных источников изменчивости. Оче-

видно, что эффективное использование латинского квадрата возможно при

том условии, что эффект всех взаимодействий равен нулю.

Разбивка по четырем символам, которая дана в табл. 20.5 один раз

ло рядам и один раз по колонкам, является типичной для латинского квад-

рата. Используя ее, надо переставлять ряды и колонки в последовательно

расположенные блоки или же выбирать такую разбивку, которая оказалась

бы столь же эффективной, как и рандомизированный способ; примеры даны

Кемпторном [332] и Кокраном и Кохом [79]. Выбор способа разбивки в латин-

ском квадрате можно сделать с помощью таблиц Фишера и Йейтса [128].

Интересное и популярное описание латинского и греко-латинского квадра-

тов, а также их комбинационных свойств см. у Гарднера [139].

20.5. ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ ЛАТИНСКОГО КВАДРАТА

ПРИ РЕШЕНИИ ГЕОЛОГИЧЕСКИХ ЗАДАЧ

Первыми, кто применил латинский квадрат, где главными эффектами

являлись 6 операторов, 6 шлифов и 6 дней, были Чейс и Фэрбэрн [59].

Базисная разбивка такого латинского квадрата 6x6 дана в приводимой ими

табл. 1. Этот эксперимент (проверка метода точечного подсчета) использовал-

348

ГЛАВА 1 г

ся для определения последовательности показаний оператора, получаемых

день за днем, а также проверки предположения, согласно которому шесть,

шлифов породы «одного из обнажений гранитов Уэстерли» являются одно-

родными по содержанию минеральных составляющих. Результаты оказались

весьма благоприятными; однако следует отметить, что если и предполагалось,

что на дисперсию оказывают влияние некоторые взаимодействия, такое пред-

положение могло бы быть и более информативным, хотя значительно полезнее

изолировать влияние взаимодействия путем классификации по трем приз-

накам. Кроме того, проверка на однородность не всегда ведет к цели, столь

непосредственно, как хотелось бы. Проверка гипотезы в общем — это по-

попытка опровергнуть предположение однородности; и если такое предпо-

ложение не оправдывается, заключение об однородности материала —

не самая большая ошибка; пока оно не вошло в обоснование сравнений,,

можно показать, что остаточный член

этом случае будет незначителен. В упо-

мянутом эксперименте для определения относительной величины дисперсии,

обусловленной неучтенными факторами, использована теоретическая бино-

миальная погрешность, а остаточный член почти равен этой теоретической

погрешности. Поэтому авторы пришли к выводу, что такой метод для оценки

соотношений минеральных компонентов этих гранитов удачен. Аналогичные

проверки изменчивости показаний операторов при точечном подсчете в шли-

фах осадочных пород (с использованием двухфакторного анализа) показали,

что снизить непоследовательность в показаниях до желаемого уровня нельзя

без большого опыта ([161; 174]; а также см. раздел 9.4 и фиг. 15.5).

Множество примеров применения латинского квадрата описано Крам-

бейном [256] и Крамбейном и Миллером [257]. При описании этих эксперимен-

тов указанные авторы подчеркивают, что использование латинского квадрата

при оценке различных факторов предшествует трехфакторному анализу [256].

Здесь опять встает проблема определения однородности; например, третий

эксперимент Крамбейна [256] представляет попытку показать, что железо-

рудная формация Негоми по всем обнажениям размером 60 X 20 футов явля-

ется однородной по мощности яшмовых и гематитовых пластов. Тут был при-

менен латинский квадрат порядка 4x4, включающий три главных эффекта::

вдоль пластов, поперек пластов π операторов. Заключение состоит в том,

что мощность пластов гематита и яшм одинакова. Ввиду того что дисперсия

ошибки относительно велика (около 50

общей суммы квадратов, связанных

с погрешностью), подобное заключение не очень информативно и может

привести к ошибочным выводам.

При попытке доказать однородность прежде всего необходимо установить

определенный критический барьер, отграничивающий те изменения, которые

еще можно считать относительно небольшими (гомогенность), от тех, которые

следует рассматривать как значительные (гетерогенность). Затем, после

того как будут ликвидированы взаимодействующие источники изменчивости,

требуется оценить степень изменчивости между пластами по отношению

к изменчивости внутри пластов. В частности, прежде всего надо оценить изме-

нения от взаимодействий между главными эффектами, например вследствие

непоследовательности показаний операторов, а затем (после того как будет

выяснено, что влиянием взаимодействий можно пренебречь) сравнить измен-

чивость между данными по пластам с соответствующей мерой внутрипласто-

вых изменений. В противном случае заключения, основанные на принятии

однородности, могут оказаться ошибочными.

Пока при решении геологических задач латинский квадрат имеет огра-

ниченное применение. Однако он может оказаться эффективным инструмен-

том в деле установления различий между средними значениями величин,

представляющих определенный интерес, если в достаточной мере будут изу-

чены данные контроля над операторами и другими взаимодействующими

источниками изменчивости, что позволит свести взаимодействие к нулю.

ПРОЧИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕШЕНИЯ

349·

Определенное преимущество рассматриваемый латинский квадрат имеет

в тех случаях, когда размеры блоков фиксированы, например при изучении

износа шин, где экспериментальной единицей является автомобиль. Такие

исследования обычно ведутся с использованием более чем одного квадрата,

чтобы можно было получить повторные замеры, необходимые для контроля

над остаточным членом (см., например, работу [79]).

20.6. НЕПОЛНЫЕ БЛОКИ - СБАЛАНСИРОВАННЫЕ

И НЕСБАЛАНСИРОВАННЫЕ

Когда требуется проанализировать очень большое количество образцов,

и, кроме того, когда для оценки погрешности нужны повторные замеры, коли-

чество наблюдений чрезмерно возрастает, а эксперимент становится длитель-

ным и дорогостоящим. В агрономических опытах при большом количестве

испытаний, т. е. образцов, требуются очень большие участки; при этом хоро-

шо известно, что различия между большими блоками больше различий между

маленькими, и поэтому возрастание неоднородности плодородия почвы огра-

ничивает размеры блоков. То же происходит в геологических исследованиях:

при большой величине блоков (слоев или площади) всегда возникает значи-

тельная неоднородность. Большое количество образцов почти во всех экспе-

риментах приводит к значительной продолжительности анализа, а измене-

ния во времени дополнительно влияют на величину остаточного члена. Изоб-

ретались сложные приемы, дающие возможность сократить размеры блоков

путем использования неполных повторений и ликвидации некоторых

эффектов, считаемых несущественными; в числе их можно назвать и описан-

ный латинский квадрат.

Детальное исследование изменений объемной плотности пород по образ-

цам 3 X 1

-дюймового керна из пачки Солт-Уош формации Моррисон (плато

Колорадо) выразилось в анализе 161 образца, полученных из скважины,

вскрывшей формацию на мощность 155 футов [157]. Этот интервал первона-

чально был разделен на четыре литологические зоны аргиллитов и песчани-

ков. Одна из двух аргиллитовых зон была разделена еще на две литологиче-

ские подзоны — на аргиллиты со сцементированными песчаниками и на толь-

ко аргиллиты. Такой стратификацией преследовалась цель увеличения гомо-

генности этих зон и подзон в отношении объемной плотности пород, что

позволило бы сократить число образцов, необходимых для характеристики

плотности в пределах каждого подразделения. Этого удалось добиться лишь

отчасти, так как плотность в пределах двух песчанистых зон менялась

в весьма широких пределах вследствие неравномерности распределения

карбонатного цемента [74, 157]. Даже при подобной стратификации (здесь

следует учесть и то, что на каждом образце проводились повторные опре-

деления) потребовалось довольно большое количество определений плот-

ности для каждой зоны \ а количество операторов, которые были необходимы

для сокращения затраты времени, колебалось от 3 до 9 [157]. Оказалось,

что изменчивость показаний операторов уменьшается по мере увеличения

количества самих операторов от 3 до 5, а затем изменчивость показаний

увеличивается, когда их били 7; очевидно, что оптимальной является бригада

в количестве 4—5 операторов. В этом исследовании применялись различные

планы эксперимента, включающие такие, как метод рандомизированных

полных сбалансированных блоков и сбалансированных неполных блоков,

например квадрат и прямоугольные решетки.

Из предыдущих экспериментов по определению плотности осадков на ртутных

весах (гл. 11) уже известно, что требуется повторить измерение три раза, чтобы достичь

удовлетворительных результатов по снижению ошибки определения, если показания

операторов контролируемы настолько, что взаимодействием можно пренебречь.

350

ГЛАВА 1 г

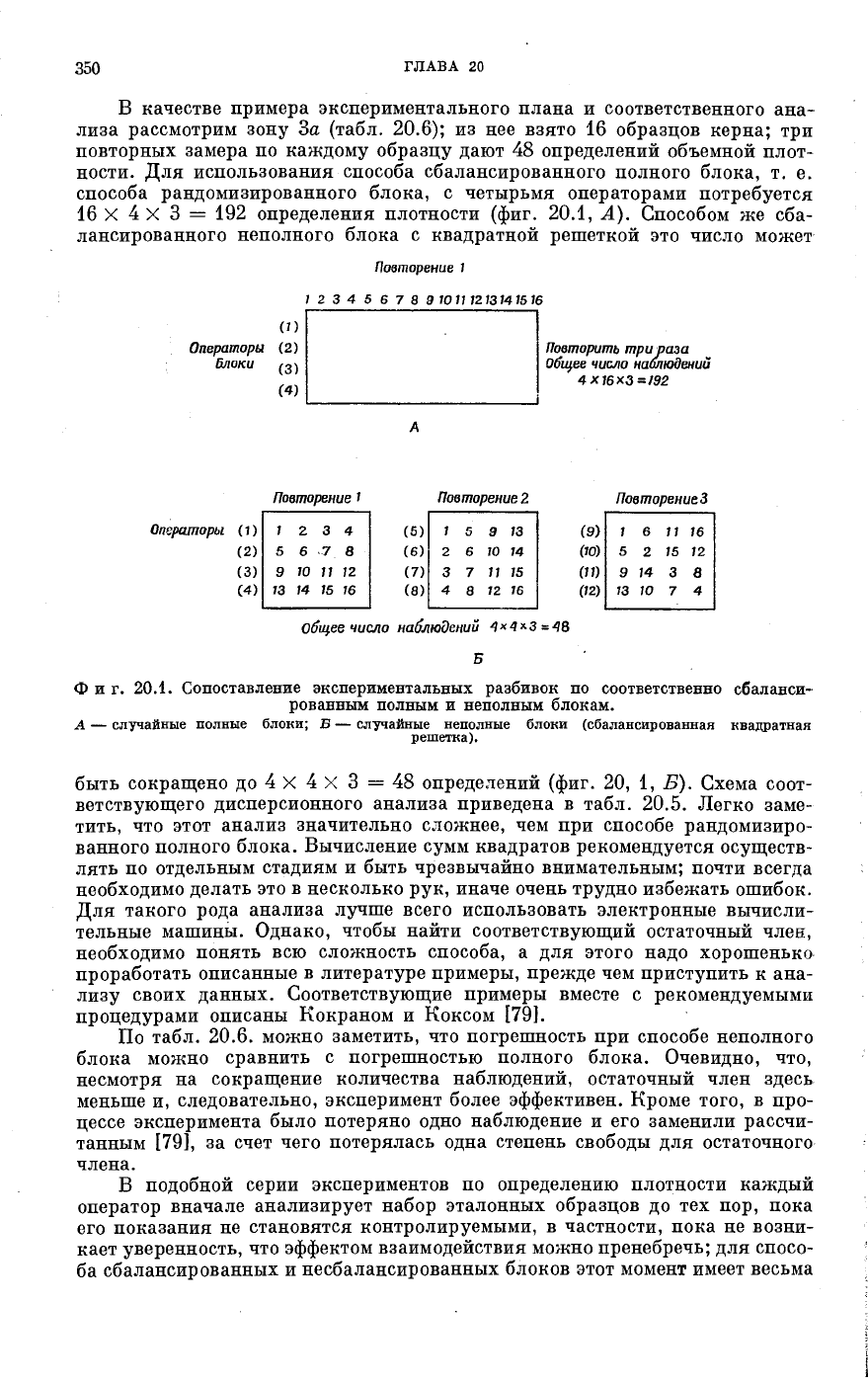
В качестве примера экспериментального плана и соответственного ана-

лиза рассмотрим зону За (табл. 20.6); из нее взято 16 образцов керна; три

повторных замера по каждому образцу дают 48 определений объемной плот-

ности. Для использования способа сбалансированного полного блока, т. е.

способа рандомизированного блока, с четырьмя операторами потребуется

16 X 4 X 3 = 192 определения плотности (фиг. 20.1, А). Способом же сба-

лансированного неполного блока с квадратной решеткой это число может

Повторение 1

/23456789 1011 1213141516

(!)

Операторы (2)

ВЛОКи (з)

(4)

Повторить

три раза

Общее

число

наблюдений

4X16X3=132

Повторение1

Повторение

2 ПовторениеЗ

Операторы (1)

1 Z 3

(5)

(9)

11 16

(2)

7 8

(6)

2 6 JO

(10) 5

2 15

(3) 9

(7)

(11)

9 14 3

С4) 13

14 15 16

(8)

12 16

(12)

7 4

общее число наблюдений 4*4*3=48

Фиг. 20.1. Сопоставление экспериментальных разбивок по соответственно сбаланси-

рованным полным и неполным блокам.

А — случайные полные блоки; Б — случайные неполные блоки (сбалансированная квадратная

решетка).

быть сокращено до 4 X 4 X 3 = 48 определений (фиг. 20, 1, Б). Схема соот-

ветствующего дисперсионного анализа приведена в табл. 20.5. Легко заме-

тить, что этот анализ значительно сложнее, чем при способе рандомизиро-

ванного полного блока. Вычисление сумм квадратов рекомендуется осуществ-

лять по отдельным стадиям и быть чрезвычайно внимательным; почти всегда

необходимо делать это в несколько рук, иначе очень трудно избежать ошибок.

Для такого рода анализа лучше всего использовать электронные вычисли-

тельные машины. Однако, чтобы найти соответствующий остаточный член,

необходимо понять всю сложность способа, а для этого надо хорошенько

проработать описанные в литературе примеры, прежде чем приступить к ана-

лизу своих данных. Соответствующие примеры вместе с рекомендуемыми

процедурами описаны Кокраном и Коксом [79].

По табл. 20.6. можно заметить, что погрешность при способе неполного

блока можно сравнить с погрешностью полного блока. Очевидно, что,

несмотря на сокращение количества наблюдений, остаточный член здесь

меньше и, следовательно, эксперимент более эффективен. Кроме того, в про-

цессе эксперимента было потеряно одно наблюдение и его заменили рассчи-

танным [79], за счет чего потерялась одна степень свободы для остаточного

члена.

В подобной серии экспериментов по определению плотности каждый

оператор вначале анализирует набор эталонных образцов до тех пор, пока

его показания не становятся контролируемыми, в частности, пока не возни-

кает уверенность, что эффектом взаимодействия можно пренебречь; для спосо-

ба сбалансированных и несбалансированных блоков этот момент имеет весьма

ПРОЧИЕ ЭКСПЕРИМЕНТАЛЬНЫЕ РЕШЕНИЯ

351·

Таблица 20.6

Квадратная решетка, дисперсионный анализ неполными блоками:

объемная плотность 16 образцов керна нз зоны 3а, скважина 155С,

пачка Солт-Уош формации Моррисон, Уолл-Каньон, Колорадо

Данные кодированы: (BD — 2) χ 103 = χ.

Источник изменчивости

Число степе-

ней свободы

Сумма квадра-

тов

Средний квадрат]

Повторения 3

1062,67 354,22

Компонент а

(6)

4 279,09 713,18

Компонент b

(6)

1749,60 291,60

Блоки (исключенные выборки) 12

6028,69 . 502,39

Выборки (игнорируемые блоки) 15

14 792,86 986,19

Выборки (исключенные блоки)

(15)

13275,86

885,07

Ошибка (внутри блока) 321

4 579,39

143,11

Ошибка (случайный блок)

441

10 608,08

241,09

Сумма 621

26 463,61

ι Одна степень свободы потеряна за счет вычисления недостающего значения.

большое значение. Погрешности повторения колеблются в пределах от 0,01

до 0,02 единиц плотности, и колебание плотности от образца к образцу зна-

чительно превышает это значение. В общем рекомендуется провести по воз-

можности полное исследование главных причин изменчивости еще до при-

менения способа неполных блоков и тщательно и осторожно выбрать экспе-

риментальную процедуру, убедившись сначала, что экономия количества

наблюдений не отразится на возможности достигнуть намеченной цели.

Способы неполных блоков (как сбалансированных, так и несбалансиро-

ванных) увеличивают разнообразие возможных процедур и дают простор

для выбора способов отбора. Большая часть этих способов касается главным

образом сравнений средних значений, т. е. все они в общем рассматриваются

как модель фиксированного типа.

20.7. ЦЕПНЫЕ БЛОКИ - ПРИМЕР СПОСОБА

НЕСБАЛАНСИРОВАННОГО НЕПОЛНОГО БЛОКА

Способ цепных блоков был предложен как специальный прием для реше-

ния некоторых задач количественного спектрального анализа. В данной

процедуре используется пластинка, на которой помещается не более 10—12

определений. Точность их обычно высока; поэтому, чтобы добиться малой

погрешности, не требуется значительного числа повторных замеров, а метод

проверки должен быть высокочувствительным [462], так как различие между

средними здесь выражается весьма малыми значениями.

При количественном спектральном анализе на элементы-примеси одной

из главных причин «погрешности» являются различия между пластинками

как вследствие нетождественности эмульсии, так и различий в условиях

проявления после экспозиции. Пользуясь пластинкой в качестве «блока»,

можно освободить остаточный член от такого источника погрешности. Но так

как элементы-примеси обычно определяют на большом количестве образцов,

а размеры пластинки ограничены возможностью размещения 10—12 экспо-

зиций (образцов), необходимость иметь повторения приводит к способу

неполных блоков. Эти две черты — фиксированный размер блока и высокая

точность анализа — обычны для количественного спектрального анализа,

поэтому наиболее подходящим способом выборочной разбивки для этого вида

работ является способ именно неполных блоков. Первичная цепь блоков