Гриффитс Дж. Научные методы исследования осадочных пород

Подождите немного. Документ загружается.

282

ГЛАВА 1 г

ности, одно из них — по мере нарастания информации улучшается оценка

дисперсии σ

. Оценивающая процедура, предложенная выше, проводилась

именно в этом предположении.

Подобную информацию можно получить графически — с помощью диа-

граммы, представленной на фиг. 16.2. Такая графическая процедура, вероят-

но, является адекватной для приближения к оценке N. Даны несколько

примеров: 1) s = 2,0; X — μ = 0,5; тогда η = 64; 2) η = 40, s = 20, тогда

при 5-процентном уровне значимости величина X — μ должна превышать

0,64, чтобы стать значимой.

16.9. СВЯЗЬ МЕЖДУ РАЗЛИЧНЫМИ ОЦЕНКАМИ ДИСПЕРСИЙ

Существуют три оценки дисперсии, имеющие большое значение, и зави-

симость менаду ними исключительно важна для понимания роли выборочных

статистик при оценке параметров генеральной совокупности.

Мы можем Определить дисперсию генеральной совокупности σ

как

iii

^. (16.21)

i=l

а выборочную дисперсию s

как

η _

= Σ

(Xi

. (16.22)

i=l

Теперь необходимо определить наилучшую несмещенную оценку дис-

персии совокупности, полученной по выборочным данным; для этого можно

поступить следующим образом [198].

Ожидаемое значение статистики представляет собой ее среднее значе-

ние при очень большом количестве испытаний, что можно записать как

E (Z) = μ. Отсюда следует, что мы можем определить ожидаемое значение

выборочной дисперсии:

= 1Г

2 [№-μ)-(Χ-μ)Ρ

= Т

Σ ΐ№-μ)

= 2№-μ) (Χ-μ) + (Χ-μ)

]

E 2 №-μ)

= «σ

и £(Ζ-μ)

= -ί-

= τ

[

ησ%

2Ε

№

μ)

- μ)+;

= ΊΓ [™

2ΗΕ

(х- ^)

+-?]

БОЛЕЕ ОБЩИЕ КРИТЕРИИ ЗНАЧИМОСТИ. КРИТЕРИЙ СТЬЮДЕНТА 283

Тогда E (S

)^o

, но E (s

) = {(п

— 1 )/и]

, которое уменьшается за счет дей-

ствия фактора

(η—1

)/п;

Следовательно, наилучшей несмещенной оценкой дисперсии совокупности

для малых выборок будет

Надо заметить, что по мере возрастания η соотношение смещения

п/(п — 1) приближается к единице, показывая что для больших выборок

выборочная дисперсия S

стремится к значению дисперсии всей совокуп-

ности σ

. Выборочная дисперсия является состоятельной оценкой, но для

малых выборок она смещена; наилучшая же оценка в малых выборках и сос-

тоятельна, и не смещена.

2 (χι-χ)

ГЛАВА 16

Более общие критерии значимости—χ

и /^-критерии

Термин «согласие» некоторые истолковывали ошибочно, полагая, что·

чем выше значение Р, тем удовлетворительнее проверяется гипотеза.

Вероятность более 0,999, иногда приводившая к подтверждению пра-

вильности гипотез, может встретиться лишь один раз на 1000 испы-

таний... Но и в этих редких случаях рассматриваемая гипотеза так же

может оказаться ошибочной, как если бы значение P равнялось 0,001,

R. A. Fisher, Statistical Methods for Research Workers, Oliver

and Boyd, Ltd., IOth ed., pp. 80—81, 1948

17.1. ВВЕДЕНИЕ

Использовать ί-критерий Стьюдента можно только при сравнении сред-

него с некоторым ожидаемым значением или при сравнении двух средних

значений, причем используемые данные должны по крайней мере достигать-

интервального уровня информации (см. раздел 12.5). Критерием \ который

менее ограничен в своем приложении и может быть применен к данным номи-

нального или порядкового уровней, является статистика χ

(хи-квадрат).

Она применяется гораздо шире, чем критерий Стьюдента, но ей недостает спе-

цифичности ί-критерия; иначе говоря, эти две статистики приводят к кри-

териям, которые желательно использовать тогда и только тогда, когда они

подходят. В общем можно сказать, что ί-критерий Стьюдента связан со срав-

нением средних значений, а показатель χ

— более общий, со сравнением

сумм квадратов.

Статистика χ

может быть определена посредством той же теоремы, что

и ί-критерий (см. раздел 16.2).

Если величина X

нормально распределена со средним и дисперсией

, а ί = (X — μ)/σ, то ί нормально распределена со средним значением

нуль и дисперсией, равной единице. Тогда сумма квадратов η случайных

выборочных значений ί будет иметь χ

-ρ8θπρβΑβΑβΗΗθ с числом степеней

свободы ν, или

t = t\ + tl+t\+...+tl,

где ν —число степеней свободы.

Тогда можно записать:

„а №-μ)

ι (X

-μ)

2 T

2 "Γ • · ·

+^-•Яз»-^]-*!

=T-

(17Л

i=l i=l

с числом степеней свободы ν = η

—

В этой главе часто используется выборочная дисперсия s

, что для больших выбо-

рок, где η > 30, адекватно дисперсии совокупности.

БОЛЕЕ ОБЩИЕ КРИТЕРИИ ЗНАЧИМОСТИ - χ«- И F-КРИТЕРИИ

285

17.2. НЕКОТОРЫЕ ХАРАКТЕРИСТИКИ х

-РАСПРЕДЕЛЕНИЯ

-Распределение в качестве статистического критерия предложил Пир-

сон в 1900-х гг., а Фишер [125] расширил его применение, введя понятие

степеней свободы. */

-Распределение представляет распределение сумм квад-

ратов

SaH= Σ (Χ«-μ)

t=l

стандартизированных нормальных отклонений от среднего значения; его

можно записать в виде формулы [350]

dP =

ехр ( χ2(η-2)/2

£(χ2) (17.2)

2 [(re—2)/2]! V

/ '

которая выражает вероятность того, что значение χ

, определенное по слу-

чайной выборке, окажется в интервале d%

Частотные кривые, построенные по формуле (17.2), изменяются от нуля

до бесконечности; обычно считают, что они относятся к типу III кривых

Пирсона [198], когда ν = 1, соответствующая функция %

-распределения

представляет положительную половину нормальной кривой [233]. Таблицы

функции распределения χ

даются в различной форме, например в таблицах

Фишера и Йейтса [128] вероятностные значения (площади, ограниченной

этими кривыми) перечислены в головках столбцов, а степени свободы

η обозначаются строками, значения же χ

составляют массив таблицы. Ана-

логичную таблицу составили также Аркин и Колтон [15]. Кендалл [233]

приводит таблицу Фишера и Йейтса в виде графика. В большинстве случаев

таблицы составлены для значений ν вплоть до 30; для величин, превышаю-

щих 30, χ

необходимо оценивать приближенно; некоторые аспекты такой

оценки рассмотрены Кендал лом [233]; при этом, следуя рекомендациям

Фишера [127], можно использовать, что величина ]/

2χ

нормально распре-

делена со средним l/2v — 1 и дисперсией, равной единице. Значения χ

с учетом степеней свободы можно ввести в формулу

= ^lty

(17.3)

и полученное значение t сравнить затем со значениями, приведенными в таб-

лице нормального распределения с параметрами 0,1 (см., например, рабо-

ту [15]). Следует отметить, что данные вероятности относятся только к одной

половине стандартной нормальной кривой; пример см. в разделе 17.7.

17.3. ПРИМЕНЕНИЕ χ

ПРИ ПОСТРОЕНИИ ДОВЕРИТЕЛЬНОГО

ИНТЕРВАЛА ДЛЯ ДИСПЕРСИИ

Определив, что χ

= Tis

, можем найти по соответствующим табли-

цам [15] при заданном числе степеней свободы ν величину χ®, которая будет

меньше Tis

, и значение χ

, которое превышает Tis

02 %2·

Если, например, выбраны 98- и 2-процентные уровни χ

для некоторого

значения ν, то интервал между двумя значениями χ

будет включать 96%

площади такого χ* -распределения. Вышеприведенное неравенство более

удобно переписать в несколько ином виде:

res

2 %2>

1 O

286

ГЛАВА 1 г

Если задано некоторое множество выборочных значений, можно оценить

и ν; подставив в это неравенство подходящие значения χ

и χ

, получим

необходимый доверительный интервал, который будет с заданной вероятно-

стью включать значение σ

Предположим, например, что имеем дело с выборкой η = 20, что дает

значение s = 0,65, тогда ν = η — 1 = 19; затем выбираем вероятности

0,05 и 0,95 и отыскиваем значения χ

[15], где 95-процентное значение

= 10, 117, а 5-процентное значение = 30, 144; затем, подставляя таб-

личные значения в неравенство, получаем:

20 χ 0,65

20 х 0,65

. 8,450

8,450

30,144 <

< 10,117 ' 30,144

<σ

< ю,117 '

0,280 < σ

<0,835.

Этот интервал будет накрывать истинное значение σ

для 90% случаев.

Такой интервал в общем довольно широк, что свидетельствует о нестабиль-

ности оценок дисперсии, полученных по малым выборкам. Например, если

данная выборка была представлена 20 измерениями длины кварцевых зерен

в шлифе, то стандартное отклонение 0,65 характеризует умеренно отсорти-

рованный осадок; и так как эти значения меняются от ,025 до 1,5 по мере

перехода от хорошо отсортированных осадков к плохо отсортированным,

полученный доверительный интервал охватывает большую часть этой области.

Этим можно руководствоваться при отборе зерен в шлифах для изме-

рений их размеров, рассматривая шлиф как однородную совокупность

с элементом «длина зерна». Тогда при стандартных отклонениях 0,25, 0,50,

0,75, 1,0 и вероятностных уровнях α = 90 и 98% для достижения обу-

словленных доверительных интервалов в пределах этих изменений (и стан-

дартных отклонений) требуются выборки таких размеров, какие показаны

в табл. 17.1; видно, что достаточно от 30 до 50 зерен (или измерений их длины)

Таблица 17.1

Доверительные пределы для стандартных отклонений длин кварцевых зерен,

измеренных в шлифах; однородная совокупность (значения X

даны по работе [323])

σ=0,25

σ=0,50

O=0,7 5

(J=I

Объем

выборки

1—'И, Vl

α, Vi

ниж- верх- ниж-

верх- ниж-

верх-

выборки

ний ний

ний ний ний ний ний

ний

предел

предел предел предел предел предел

α=95% v=re—1

11,0705

1,1455 0,0282 0,2728 0,1129

1,0912

0,2541 2,4553

0,527

7,035

10 18,3070 3,9403

0,0341

0,1586 0,1366

0,6345

0,3073

1,4276

0,591 3,007

24,9958

7,2609

0,0375

0,1291

0,1500

0,5165 0,3376

1,1620

0,633 2,283

20 31,4104

10,8508

0,0398 0,1152

0,1592

0,4608 0,3582 1,0368

0,664

1,977

37,6525

14,6114

0,0415

0,1069

0,1660

0,4277

0,3735

0,9624

0,687 1,805

43,7729

18,4926

0,0428 0,1014

0,1713

0,4056

0,3855

0,9125 0,705 1,694

55,7585 26,5093

0,0448

0,0943

0,1793

0,3772

0,4035 0,8488 0,717 1,509

50 67,5048

34,7642 0,0463

0,0899

0,1852

0,3596

0,4166

0,8090

0,741

1,438

90,5312

51,7393 0,0483

0,0846

0,1933

0,3382 0,4349

0,7610

0,773

1,353

100

124,342

77,9295

0,0503

0,0802 0,2011

0,3208

0,4524

0,7218

0,804

1,283

α= 99%

v=re—1

15,0863

0,5543

0,0207 0,5638 0,0829

2,2551

0,1864 5,0740

0,3314

9,0203

10 23,2093

2,5582

0,0269

0,2443

0,1077 0,9777 0,2424 2,1988 0,4309

3,9090

15 30,5779 5,2294

0,0307

0,1793

0,1226 0,7171

0,2759 1,6135 0,4906

2,8684

37,5662

8,2604 0,0333

0,1513 0,1331

0,6052

0,2995 1,3619

0,5324 2,4212

44,3141

11,5240 0,0353

0,1356

0,1410

0,5423

0,3173

1,2203

0.5642 2,1694

50,8922

14,9535

0,0368

0,1254

0,1474

0,5016

0,3316

1,1285

0,5895

2,0062

63,6907 22,1643

0,0393 0,11:28 0,1570

0,4512

0,3533

1,0150 0,6280

1,8047

76,1539

29,7076 0,0410 0,1052 0,1641

0,4208

0,3693

0,9467 0,6566

1,6831

100,425 45,4418

0,0436

0,0963

0,1743

0,3851

0,3921

0,8665

0,6970

1,5404

100 135,807

70,8648

0,0460

0,0892 0,1841

0,3568

0,4142 0,8028 0,7363 1,4273

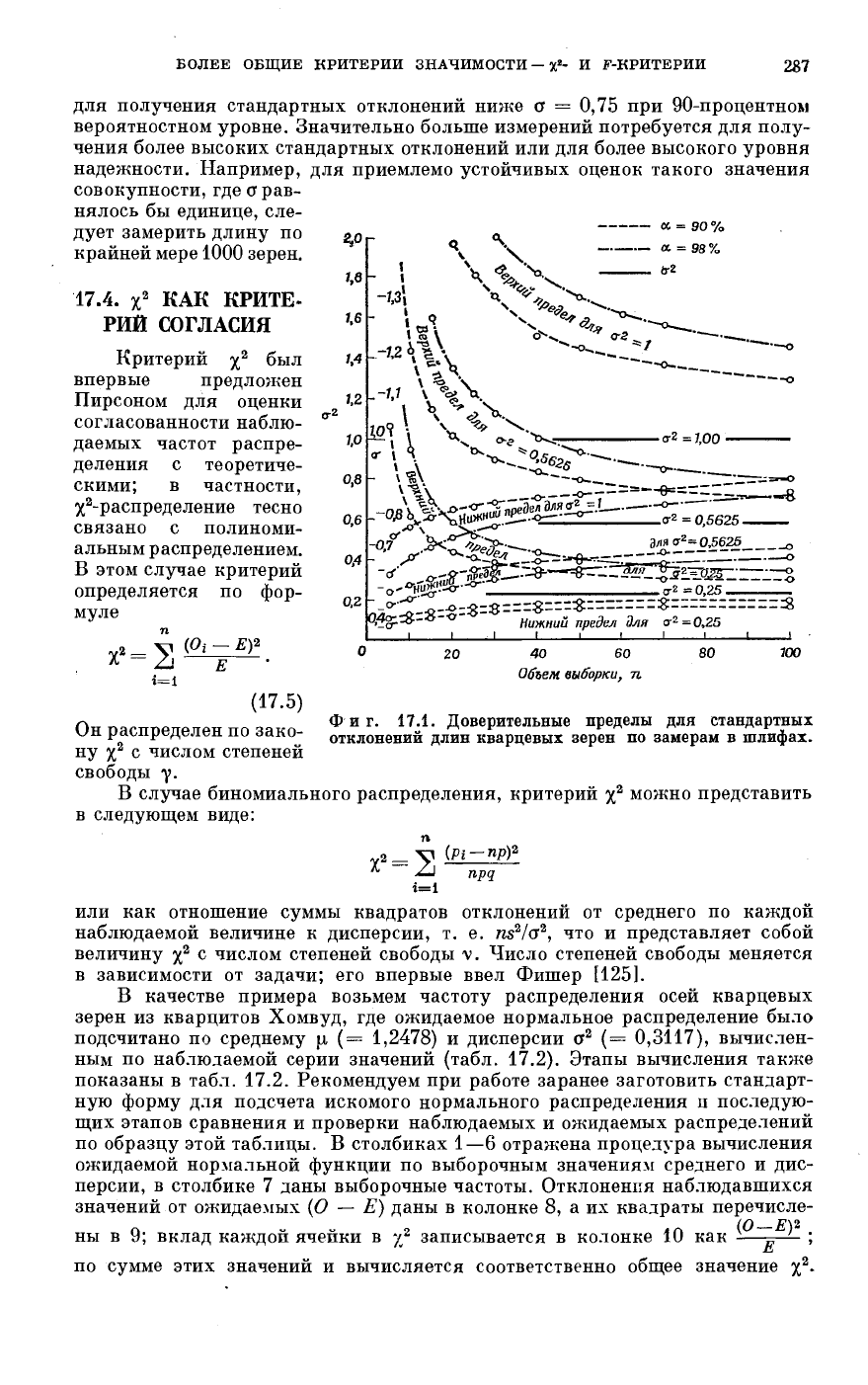
БОЛЕЕ ОБЩИЕ КРИТЕРИИ ЗНАЧИМОСТИ - χ«- И F-КРИТЕРИИ

287

для получения стандартных отклонений ниже σ = 0,75 при 90-процентном

вероятностном уровне. Значительно больше измерений потребуется для полу-

чения более высоких стандартных отклонений или для более высокого уровня

надежности. Например, для приемлемо устойчивых оценок такого значения

совокупности, где а рав-

нялось бы единице, сле-

дует замерить длину по

крайней мере 1000 зерен.

17.4. χ

КАК КРИТЕ-

РИЙ СОГЛАСИЯ

Критерий χ

был

впервые предложен

Пирсоном для оценки

согласованности наблю-

даемых частот распре-

деления с теоретиче-

скими; в частности,

-распределение тесно

связано с полиноми-

альным распределением.

В этом случае критерий

определяется по фор-

муле

гр

',в

'.6

',2

1,0

0,8

0,6

0,4

0.2

i=l

(Of - E^

X %

чч

W »

со

й \

_-1,1 \

I W\

α, = 90 %

α = 98%

й-2

о-г.

-σΖ =7,00 •

t*.

—о---==—= -

—β

= 0,5625 -

Зля

0,5625_

0,4cr Нижний предел для σ

=0,25

I I.I ι I I I I I I

80 100 40 60

Объем выборки, τι

(17.5)

Он распределен по зако-

ну χ

с числом степеней

свободы у.

В случае биномиального распределения, критерий χ

можно представить

в следующем виде:

Фиг. 17.1. Доверительные пределы для стандартных

отклонений длин кварцевых зерен по замерам в шлифах.

i=l

(Ρί-ηρ)

npq

или как отношение суммы квадратов отклонении от среднего по каждой

наблюдаемой величине к дисперсии, т. е. res

, что и представляет собой

величину χ

с числом степеней свободы v. Число степеней свободы меняется

в зависимости от задачи; его впервые ввел Фишер [125].

В качестве примера возьмем частоту распределения осей кварцевых

зерен из кварцитов Хомвуд, где ожидаемое нормальное распределение было

подсчитано по среднему μ (= 1,2478) и дисперсии σ

(= 0,3117), вычислен-

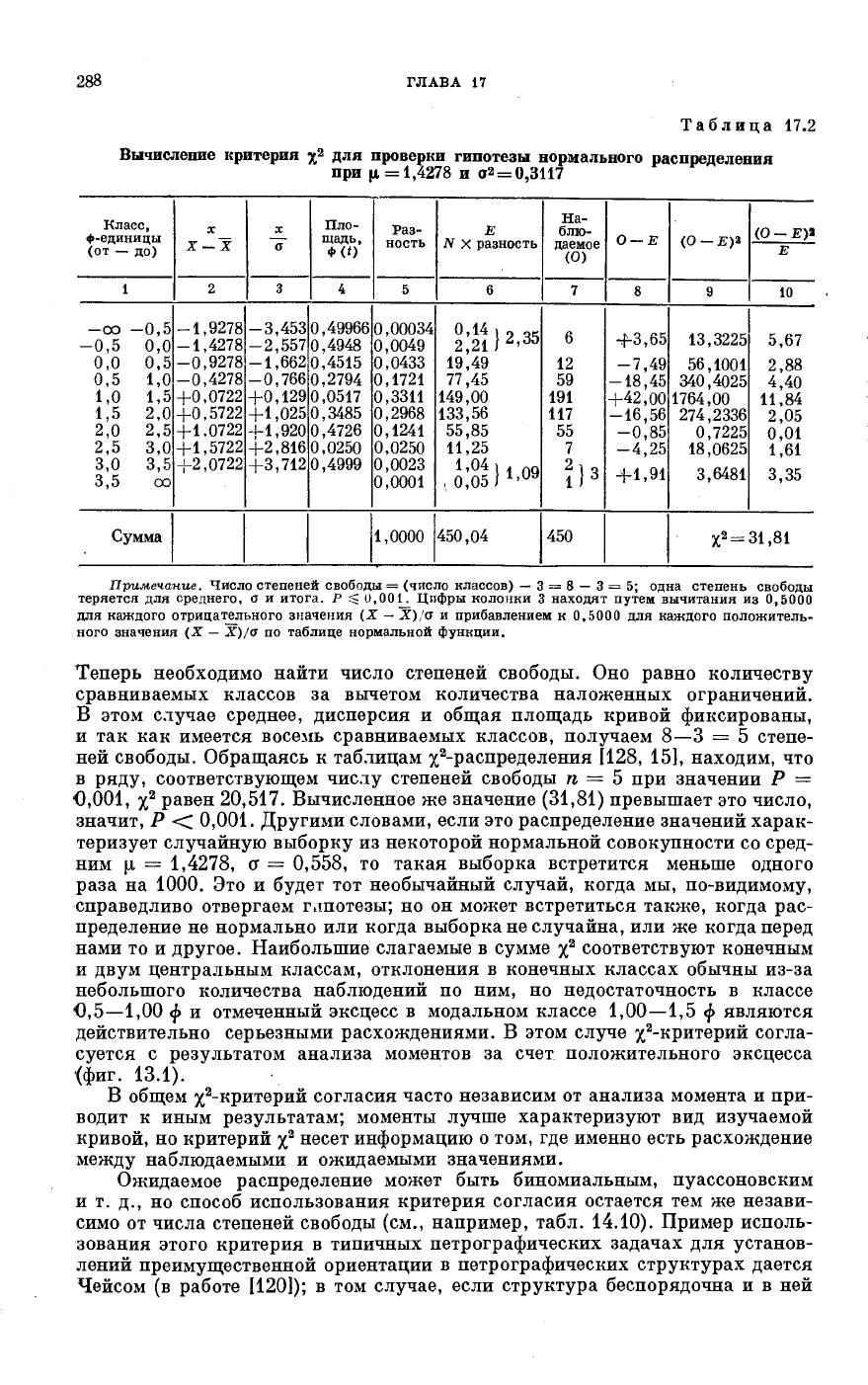
ным по наблюдаемой серии значений (табл. 17.2). Этапы вычисления также

показаны в табл. 17.2. Рекомендуем при работе заранее заготовить стандарт-

ную форму для подсчета искомого нормального распределения π последую-

щих этапов сравнения и проверки наблюдаемых и ожидаемых распределений

по образцу этой таблицы. В столбиках 1—6 отражена процедура вычисления

ожидаемой нормальной функции по выборочным значениям среднего и дис-

персии, в столбике 7 даны выборочные частоты. Отклонения наблюдавшихся

значений от ожидаемых (О — Е) даны в колонке 8, а их квадраты перечисле-

о 2 лп (О —Ep .

ны в У; вклад каждой ячейки в yf записывается в колонке IU как —;

по сумме этих значений и вычисляется соответственно общее значение χ

288 ГЛАВА 1 г

Таблица 17.2

Вычисление критерия χ

для проверки гипотезы нормального распределения

при μ = 1,4278 и

= 0,3117

Класс,

Ф-единицы

(от — до)

X-X

ОС

~с

Пло-

щадь,

(О

Раз-

ность

N X разность

На-

блю-

даемое

(О)

O-E

(О

—

Е)2

(О

— Е>а

Класс,

Ф-единицы

(от — до)

X-X

ОС

~с

Пло-

щадь,

(О

Раз-

ность

N X разность

На-

блю-

даемое

(О)

O-E

(О

—

Е)2

2 3

-OO -0,5

-0,5 0,0

0,0 0,5

0,5 1,0

1,0 1,5

1,5 2,0

2,0 2,5

2,5 3,0

3,0 3,5

3,5 сю

-1,9278

-1,4278

-0,9278

-0,4278

+0,0722

+0,5722

+1.0722

+1,5722

+2,0722

-3,453

-2,557

-1,662

-0,766

+0,129

+1,025

+1,920

+2,816

+3,712

0,49966

0,4948

0,4515

0,2794

0,0517

0,3485

0,4726

0,0250

0,4999

0,00034

0,0049

0,0433

0,1721

0,3311

0,2968

0,1241

0,0250

0,0023

0,0001

0,14 ι 2 „с

2,211

19,49

77,45

149,00

133,56

55,85

11,25

1,04

1 09

, 0,05

иа

191

117

+3,65

-7,49

-18,45

+42,00

-16,56

-0,85

-4,25

+1,91

13,3225

56,1001

340,4025

1764,00

274,2336

0,7225

18,0625

3,6481

5,67

2,88

4,40

11,84

2,05

0,01

1,61

3,35

Сумма

1,0000

450,04

450

= 31,81

Примечание. Число степеней свободы = (число классов) — 3 = 8 — 3 = 5; одна степень свободы

теряется для среднего, σ и итога. P U

OOb Цифры колонки 3 находят путем вычитания из 0,5000

для каждого отрицательного значения (X

—

Х)/а и прибавлением к 0,5000 для каждого положитель-

ного значения (X — Х)/а по таблице нормальной функции.

Теперь необходимо найти число степеней свободы. Оно равно количеству

сравниваемых классов за вычетом количества наложенных ограничений.

В этом случае среднее, дисперсия и общая площадь кривой фиксированы,

и так как имеется восемь сравниваемых классов, получаем 8—3 = 5 степе-

ней свободы. Обращаясь к таблицам х

-распределения [128, 15], находим, что

в ряду, соответствующем числу степеней свободы η = 5 при значении P =

0,001, χ

равен 20,517. Вычисленное же значение (31,81) превышает это число,

значит, P <С 0,001. Другими словами, если это распределение значений харак-

теризует случайную выборку из некоторой нормальной совокупности со сред-

ним μ = 1,4278, σ = 0,558, то такая выборка встретится меньше одного

раза на 1000. Это и будет тот необычайный случай, когда мы, по-видимому,

справедливо отвергаем глпотезы; но он может встретиться также, когда рас-

пределение не нормально или когда выборка не случайна, или же когда перед

нами то и другое. Наибольшие слагаемые в сумме χ

соответствуют конечным

и двум центральным классам, отклонения в конечных классах обычны из-за

небольшого количества наблюдений по ним, но недостаточность в классе

0,5—1,00 φ и отмеченный эксцесс в модальном классе 1,00—1,5 φ являются

действительно серьезными расхождениями. В этом случе "/

-критерий согла-

суется с результатом анализа моментов за счет положительного эксцесса

{фиг. 13.1).

В общем χ

-κρΗΤβρπή согласия часто независим от анализа момента и при-

водит к иным результатам; моменты лучше характеризуют вид изучаемой

кривой, но критерий χ

несет информацию о том, где именно есть расхождение

между наблюдаемыми и ожидаемыми значениями.

Ожидаемое распределение может быть биномиальным, пуассоновским

и т. д., но способ использования критерия согласия остается тем же незави-

симо от числа степеней свободы (см., например, табл. 14.10). Пример исполь-

зования этого критерия в типичных петрографических задачах для установ-

лений преимущественной ориентации в петрографических структурах дается

Чейсом (в работе [120]); в том случае, если структура беспорядочна и в ней

БОЛЕЕ ОБЩИЕ КРИТЕРИИ ЗНАЧИМОСТИ - χ«- И F-КРИТЕРИИ

289

не обнаружено преобладающего направления в ориентации, а в каждом

классе ожидается равное количество замеров, ожидаемое распределение, сле-

довательно, должно быть равномерным, или прямоугольным (см. также рабо-

ту [156]); ожидаемые частоты внутри классов могут быть найдены путем

деления общего числа наблюдений на количество классов. Наблюдаемое рас-

пределение затем можно сравнить с ожидаемым и использовать χ

в качестве

критерия согласия. Если гипотеза равномерного распределения отклонена,

значит, некоторый класс (или классы) содержит эксцесс наблюдений и в дан-

ном образце породы, видимо, преобладает какое-то структурное направление.

Для палеонтолога больший интерес представляет использование в ка-

честве ожидаемых распределений родовых отношений; такое исследование

особей по выборке часто применяется для доказательства связей, жизнеспо-

собности и т. д. [127, 289, 409].

17.5. ТАБЛИЦЫ СОПРЯЖЕННОСТИ ПРИЗНАКОВ И χ

Использование критерия χ

в таблице сопряженности признаков для

решения геологических задач было впервые предложено Эйзенхартом [107].

Это очень важная область применения статистических критериев как в ла-

бораторных, так и при полевых геологических исследованиях. По существу,

наблюдения классифицируют по определенным признакам, представляющим

интерес, и возникает вопрос, являются ли эти признаки независимыми? Пред-

положим, например, что геолог разделил серию образцов из одного или более

обнажений на два класса по их окраске (красные и зеленые) и на два же клас-

са по размерности зерен (крупнозернистые и тонкозернистые); эти наблю-

дения можно было бы представить в виде частот, как это сделано в табл. 17.3.

Таблица 17.3

Таблица распределения 240 образцов пород,

классифицированных по цвету и размерам зерен

(модельный пример)

Размер зерен

Цвет

Общее коли-

чество

Размер зерен

красный

зеленый

Общее коли-

чество

Крупный

Тонкий

120

150

Сумма

160

80 240

Возникает вопрос, как на основе такой информации решить —«зависит ли

зернистость фракции, представленной данными образцами, от цвета пород»?

Важно понять, что подобную таблицу сопряженных признаков порядка

2x2 можно обобщить и обработать в связи с той или иной гипотезой доста-

точно строго [464]. Обозначим выбранные признаки как А (цвет) и В (размер);

тогда серия геологических образцов может быть классифицирована как А

и «не Аь (А, пли а) и как В и «не В» (В, или β). Обозначим частоту встре-

чаемости признака А во всей серии как (А), признака В (как (В), а как (а)

и β как (β) (табл. 17.4).

Если между признаками А и В нет связи, следует ожидать, что А среди

В распределено в такой же пропорции, как и среди «не В». Мы можем опре-

делить два таких несвязанных признака как независимые, тогда в качестве

критерия независимости для А и В будем иметь:

т-ш (17.6)

(В)

(β)

19-429

290 ГЛАВА 17

Таблица 17.4

Обобщенная таблица сопряженных признаков

порядка 2X2

Признак 1

Признак 2

Итог

(AB)

ИР) «

(А)

(аВ)

(αβ)

(а)

Сумма

(B)

(P)

Отсюда следует:

Аналогично

, (AB) , (Λβ) _

_(АВ)_ _

(Λβ)

(В) -

(β) (В) (β)

(α£)/(5) = (αβ)/(β);

По этой таблице можно вывести, конечно, и многие другие эквивалент-

ные взаимоотношения между частотами, которые удовлетворяли бы условиям

независимости [464]; возможно, наиболее привычным из них явилось бы такое

условие: «если признаки А и В независимы, то доля AB в данной совокупно-

сти (формации) равна доле А, умноженной на долю В», т. е.

(AB) (Л) (В) .,

7Я

Это правило — основное для характеристики независимости во всех

видах статистического анализа.

Предположим теперь, что характерные признаки А и В каким-то обра-

зом связаны; тогда можно написать [464]:

1. Если то А и В коррелируются положительно (17.9а)

2. Если (AB) < , то А и В коррелируются отрицательно (17.96)

Важно заметить, что такая корреляция основана на независимости; сле-

довательно, А ж В сичитаются коррелирующимися тогда и только тогда,

когда они встречаются совместно чаще, чем это можно было бы ожидать

в случае их независимости.

Связь не может быть обнаружена, когда некоторые А равны некоторым

В, как бы ни велики были их количественные соотношения. Следует отметить,

что в приведенной таблице классы даются по номинальной шкале (например,

«красный, зеленый») или порядковой (например, крупнозернистый > мелко-

зернистый) и эти количества являются частотами, определяемыми при под-

счете; следовательно, такая процедура применима во всех случаях измерения

«состава» там, где элементы совокупности классифицированы по характер-

ным признакам, которые могут быть как связанными, так и несвязанными.

Разумеется, иногда полезно использовать тот тип классификации для резуль-

татов измерений по интервальной шкале и шкале отношений, который исполь-

зуется в критериях согласия.

Возвращаясь к критерию независимости, из равенства (17.8) можем

найти (AB) по (.4), (В) и (N)

если предположим, что характерные признаки

независимы. К тому же, так как (AB) + (^4) = (А), можем определить (А)

и аналогично (аВ) и (αβ); очевидно, что, если одна из клеток в таблице

БОЛЕЕ ОБЩИЕ КРИТЕРИИ ЗНАЧИМОСТИ — χ«- И F-КРИТЕРИИ

291

(О—Ep

сопряженных признаков с обозначением частот заполнена и дано общее коли-

чество, все остальные клетки также считаются фиксированными при числе

степеней свободы 1. Возможно также составить таблицу ожидаемых частот

в условиях гипотезы независимых и наблюдаемых частот. По такому набору

можно вычислить статистику χ

1=1

которая будет иметь "^-распределение с заданным числом степеней свободы,

если гипотеза независимости верна. Следовательно, можно проверить пред-

положение о независимости набора частот. Ожидаемые значения для приме-

ра, заданного табл. 17.3, даны в табл. 17.5.

Таблица 17.5

Ожидаемые частоты для образцов пород,

расклассифицированных по цвету и размерности зерен.

Гипотеза: признаки взаимонезависимости

Размер зерен

цвет

Итого

Размер зерен

красный зеленый

Итого

Крупный

Мелкий

100

150

Сумма

160 80 240

Тогда χ

= §

i = ι

, 20

Дает χ

(-20)

60 50

20¾

= 23,66.

Заметим, что суммы отклонений (О — Е) равны нулю для каждого ряда

и колонки по всей таблице. Теперь можем использовать таблицы χ

для

отыскания в них величины, близкой значению χ

= 23,66 при числе степе-

ней свободы ν = 1. Находим, что при 5-процентном уровне значимости

) X

= 3,841 а при 0,1-процентном уровне (P

001

) χ

= 10,827. Так как

вычисленное значение χ

превышает последнее, можем сказать, что если

гипотеза H

независимости цвета и размеров зерен и верна для данной сово-

купности, то такая выборка встретится случайно или при случайном опробо-

вании этой формации не чаще, чем один раз на 1000. Так как такая частота

весьма мала, мы отвергаем гипотезу, рискуя при этом ошибиться в случае

повторения испытаний не более одного раза на 1000.

Так как, согласно распределению частот, признаки цвета и размерности

не независимы, может возникнуть желание изучить их возможные взаимоот-

ношения путем сравнения (AB) и (.4) (B)IN, как это дано в приведенных выше

неравенствах (17.9а) и (17.96):

120 > 150 X Цд= 100.

Следовательно, А и В связаны положительно, и в нашем примере гру-

бозернистые слои чаще будут иметь красную окраску, а тонкозернистые —

зеленую. Возможно, надо подчеркнуть, что «направление» связи действи-

тельно имеет смысл, только когда признаки даются по порядковой шкале,

однако эта связь является типичной для любой таблицы 2x2.

19*