Гриффитс Дж. Научные методы исследования осадочных пород

Подождите немного. Документ загружается.

ГЛАВА 1 г

Среднее X вычислено по выборке; следовательно, число степеней свобо-

ды ν на 1 меньше числа измерений: ν = η — 1 = 8. По таблицам значений

t [15, 128] находим, что для ν = 8 P

= 3,36 (или P

001

= 5,041) значение

10 сильно превышает то и другое; отсюда, если гипотеза верна, такая выбор-

ка измерений должна встречаться гораздо реже, чем один раз на 1000. Сле-

довательно, гипотезу случайного выбора из нормальной совокупности

с μ = 0 м0жно отвергнуть.

Если же в ином случае находим, что а = 6,0, где X = 2 ф, are = 9, то

(2-0)У9

=1Д

Такое значение t = 1 при ν = 8 встречается гораздо чаще, чем десять раз

на 100 [15]; если же используем таблицы Фишера и Йетса [128], с большей

определенностью сможем сказать, что это значение t в условиях случай-

ности отбора встречается от 30 до 40 раз на каждые 100 случаев. Подобное

положение довольно обычно и не противоречит сформулированной гипотезе.

В таком случае.и равенство μ = 0 весьма вероятно; подобное различие между

этими двумя критериями свидетельствует об эффективности меры изменчи-

вости для проверки гипотез.

Несколько более общее утверждение может быть сделано с использо-

ванием доверительного интервала; так, при нормальном распределении около

95% измерений заключено в пределах μ ± 1,96 σ, что можно выразить

иначе:

Τ + 1,96σ>μ>Χ-1,96σ. (16.8)

Интервалу μ ± 1,96σ соответствует около 95% площади нормальной

кривой; теперь, использовав вместо этого коэффициента эквивалентное зна-

чение ί-критерия Стьюдента, мы можем заменить σ на σ-^ и получить

—

ώχ<.μ<:Χ + ώ

. (16.9)

Затем можно подставить из первичного значения X = 2φ, σ-^ = 0,2

и η = 9, тогда

— 0,2ί<μ<2 + 0,2ί,

и для числа степеней свободы при 8- и 95-процентном уровне вероятности

ί = 2,31, откуда

2 - 0,2 χ 2,31 < μ < 2 + 0,2 χ 2,31;

—

0,462 < μ < 2

-f-

0,462,

ддд

1,538 <μ< 2,462.

Среднее μ может лежать в пределах этого интервала или за его преде-

лами; если повторить эксперимент и заново вычислить этот интервал по ново-

му σ, то в среднем 95% таких интервалов будут содержать μ. Или же, вероят-

ность того, что любой из интервалов содержит μ, будет равна 95% [293].

Предположим теперь, что вторая случайная выборка из девяти длинных

осей кварцевых зерен дает среднее в 3,00 единиц; тогда эта серия наблю-

дений отличается от первоначальной при 95-процентном уровне значимости·

Во втором случае с X = 2, σ = 6,0 и к = 9 доверительный интервал

становится

2-2,0 χ 2,31 <μ< 2 + 2, 2,0x2,3,

—

2,62

<С

μ < 6,62.

БОЛЕЕ ОБЩИЕ КРИТЕРИИ ЗНАЧИМОСТИ. КРИТЕРИЙ СТЬЮДЕНТА 273

В этом случае значение μ = 0 довольно вероятно; чтобы получить

среднее с такой же точностью, по этим доверительным границам надо уве-

личить размер выборки пропорционально квадрату п. Предположим, мы уве-

личиваем размер выборки до η = 81, оставляя прежнее значение стандарт-

ного отклонения и среднего; тогда βχ — — 0,667, и при 95-процентном

вероятностном уровне значение t для числа степеней свободы ν = 80 будет

равным 1,99. Отсюда:

—

ώχ < μ <X — ta

;

2 - 1,99 χ 0,667 < μ < 2 +1,99 χ 0,667;

2 -1,327 <μ< 2 +1,327;

0,673 < μ < 3,327.

Теперь мы можем отвергнуть гипотезу, что μ = 0 при 5-процентном

уровне значимости; при большей изменчивости затраты по уменьшению

доверительного интервала значительно увеличиваются.

16.4. СРАВНЕНИЕ СРЕДНИХ ДВУХ ВЫБОРОК

ί-Критерий подходит также и для проверки следующей гипотезы: «эти

две выборки случайны и принадлежат одной нормальной совокупности».

Вначале мы можем рассмотреть предположение, что эти две выборки объе-

мами Ti

и п

независимо взяты из нормальной совокупности со средним

μ и дисперсией σ

соответственно. Затем различие между средними

— μ) — (X

— μ) сравнивается с наилучшей несмещенной оценкой

дисперсии разности X

— X

; μ исчезает из числителя и различие средних

превращается в X

— X

. Тогда

Xl-Xz

(16.10)

Теперь надо вычислить несмещенную оценку дисперсии, сделав разли-

чия между X

и Х

2г

. Дисперсию суммы или разности двух нормальных

случайных величин можно определить как

Var (X

+ X

) = o\ + al + 2р O

; (16.11а)

Var (X

- X

) = ol +al- 2ра,а

. (16. lib)

Тогда, если две случайные выборки независимы, коэффициент корреля-

ции между X

и X

обозначен через р = 0, дисперсия этой суммы (раз-

ности) примет вид

VariX

± X

) =

+ ^.. (16.12)

Аналогично дисперсия суммы или разности между средними из незави-

симых выборок, относящихся к нормальной совокупности, будет

Var(X

1±

) = ^

i +

= i + i. (16.13)

Если верна упомянутая выше гипотеза и эти две случайные выборки

действительно взяты из нормальной совокупности, то

= O^ =

(16.14)

18—429

274

ГЛАВА 1 г

Var(X

-X

) =

(J- + J-) ,

или

χι-χ

νΊΡ^ =

/¾? · <

Теперь по'выборкам 1 и 2 можем вычислить

-2 Sxl ~2 Sxl

σ, = —Ц- И

σ„

" "

Z — 1

или, комбинируя эти две оценки, получаем, что

т2 — гг

I гг

Sx\ + Sxl

1»1 + И2 —2

Но

и Sx

Тогда (

I+ ^l

(исходя из выборочных дисперсий)или

Q _ -, / η A

V ηι-\-η

— 2

=/¾¾ /¾?. (М-«Ч

-ХГ F п

-\-п

—2 Г B

ИЛИ

-X

Теперь вернемся к гипотезе о случайном характере этЬх двух выборок

и их принадлежности некоторой одной нормальной совокупности и вычислим

статистику t:

t= . _ Xi-Xz

(1618)

которая подчиняется ί-распределению Стьюдента с v = n

—

2 степенями

свободы.

Если

то формула сводится к

-X

2 =

-X

(16 19V

V(«i + 4)/« V2n/(2i»-2) V(sf + «!)/("-1) '

которая распределена по закону Стьюдента с ν = 2 (η — 1) степенями

свободы.

16.5. ПРИМЕРЫ ПРИМЕНЕНИЯ f-КРИТЕРИЯ СТЬЮДЕНТА

ДЛЯ СРАВНЕНИЯ ДВУХ СРЕДНИХ

В одном из исследований, проведенном с целью сравнить результаты

измерений длинных осей кварцевых галек из гравия Монтурсвплл (близ

Вильямспорта) при различных способах опробования были получены сле-

Следует отличать выборочные дисперсии s

и наилучшую несмещенную оценку

дисперсии совокупности от σ

(см. раздел 16.9).

БОЛЕЕ ОБЩИЕ КРИТЕРИИ ЗНАЧИМОСТИ. КРИТЕРИЙ СТЬЮДЕНТА 275

дующие статистики (средние выражены в ф-единицах):

= 4,571; о

= 0,6673; щ = 336;

= 5,547; о* = 0,5628;

щ,

= 324.

Подлежит проверке нулевая гипотеза H

: «эти две выборки случайны и отно-

сятся к одной нормальной совокупности».

Заметим, что дисперсии S

в равенствах (16.18) и (16.19) выборочные,

поскольку эти значения, вычисленные для образцов из гравия Монтурсвилл,

являются наилучшими оценками. Следовательно, необходимо умножить

эти лучшие оценки σ

соответственно на (^

— 1)/«ι и (п

— 1)/^2, что дает

= 0,665314 и S

= 0,561063. Тогда

£ X

-X

У sf/n

+S^n

У (B

+ H

JAn

+«2—2)

5,547—4,571

~~ У0,6653/324 + 0,5611/336 У660/658 ~~

0,976

~ у405,3372/108,864 У 1,003039 ~

^ 0,976

0,976 ^

15 971

У0,003723 У1,003039 0,06111 '

при числе степеней свободы ν = U

+ п

— 2 = 324 + 336 — 2 = 658.

Такое значение t очень велико (P < 0,001). Другими словами, если нулевая

гипотеза верна, такое различие может встретиться гораздо реже, чем один

раз на 1000. Приходится отвергнуть эту гипотезу, и так как имеется две

выборки заведомо из одной и той же совокупности, а в подобном частном

случае истинное распределение, вероятнее всего, будет ф-нормальным [170],

то это приведет к выводу о неслучайности отбора.

16.6. ПРОВЕРКА БОЛЕЕ СЛОЖНЫХ ГИПОТЕЗ

Бокман [31], описывая петрографию формаций Стенли и Джэкфорк,

пишет:

«В связи с изучением распределения размеров зерен была предпринята попытка

определить, обладают ли песчаники Стенли и Джэкфорк градационной зернистостью...

Из верхних и нижних частей пластов различной мощности были собраны сколки пород

и из них приготовлены шлифы... Было изучено семь пластов мощностью от 9 до 52 дюй-

мов. Результаты измерений представлены в табл. 1... И хотя как будто и наблюдается

некоторый градационный эффект от подошвы к кровле пластов, все же встает вопрос,

действительно ли это градационная зернистость».

Если мы примем в качестве признака градационной слоистости общее

уменьшение зернистости от подошвы к кровле слоя, то можно использо-

вать данные табл. 16.1 для проверки эффективности такого признака. Нуле-

вая гипотеза H

получает следующую формулировку: «эти выборочные

средние получены по двум независимым случайным выборкам из одной

и той же нормальной совокупности».

Подходящей аппроксимацией является нормальное распределение

(см. раздел 13.12), но если пласты обладают градационной зернистостью

и предложенный признак эффективен, то выборки ни случайны, ни незави-

симы. Для анализа подобной серии наблюдений можно предложить несколь-

ко гипотез и процедур. Если данные пласты не градационны, верхние

их части могут быть более грубозернисты, чем нижние, и наоборот, в среднем

с равной вероятностью того и другого; иными словами, имеется равная

вероятность обнаружить позитивное или негативное различие между нижней

и верхней частями слоя. Тогда мы можем определить количество позитив-

ных (шесть) и негативных (один) признаков и испытать, представляют ли они

18«

276

ГЛАВА 1 г

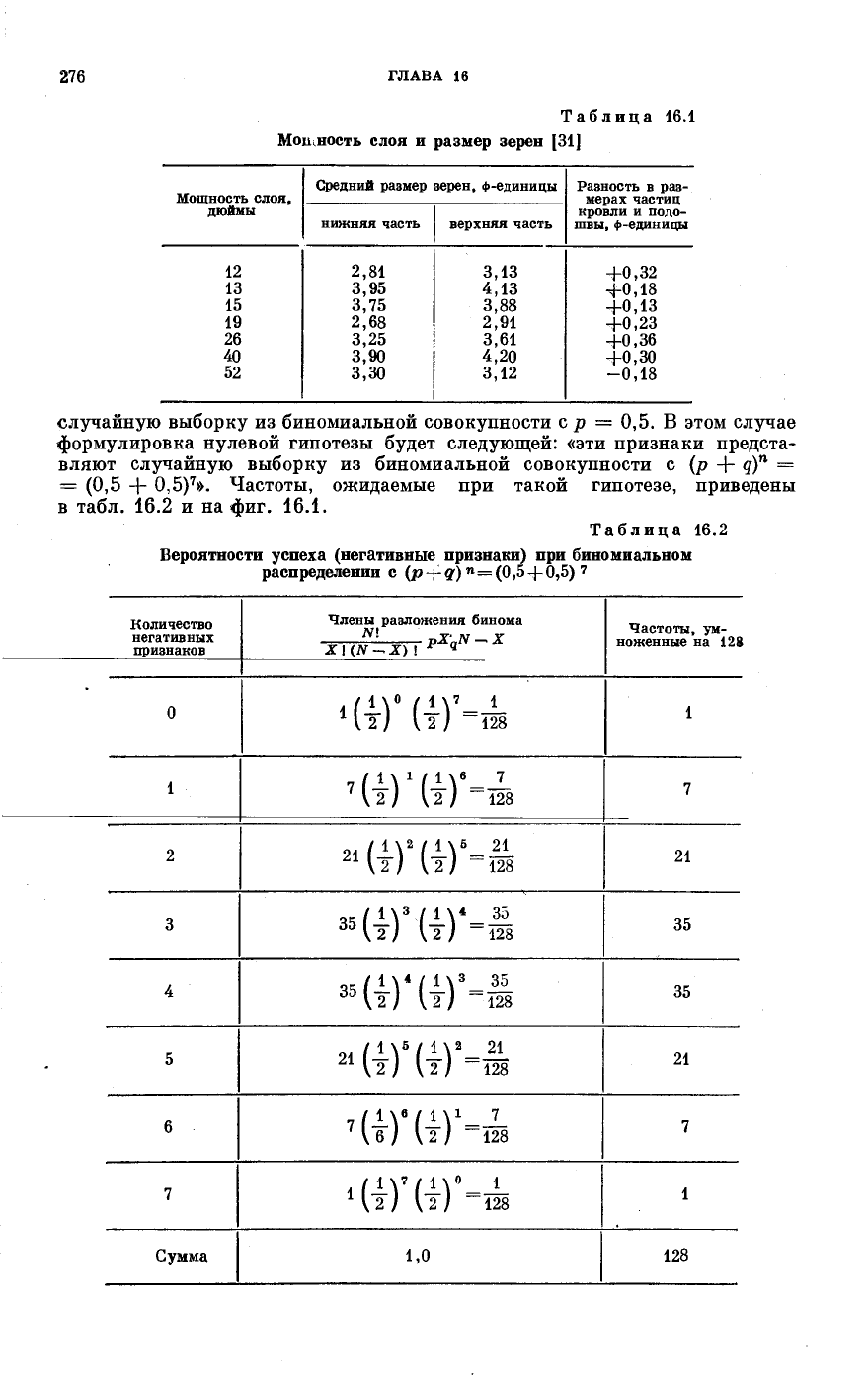
Таблица 16.1

Мошность слоя и размер зерен [31]

Мощность слоя,

Средний размер зерен, Ф-единицы

Разность в раз-

Мощность слоя,

мерах частиц

дюймы

кровли и подо-

нижняя часть

верхняя часть

швы, Ф-единицы

12 2,81 3,13

+0,32

13 3,95

4,13

+0,18

15 3,75

3,88 +0,13

2,68

2,91

+0,23

26 3,25 3,61 +0,36

40 3,90

4,20 +0,30

3,30

3,12

-0,18

случайную выборку из биномиальной совокупности с ρ = 0,5. В этом случае

формулировка нулевой гипотезы будет следующей: «эти признаки предста-

вляют случайную выборку из биномиальной совокупности с (р + q)

= (0,5 + 0,5)

». Частоты, ожидаемые при такой гипотезе, приведены

в табл. 16.2 и на фиг. 16.1.

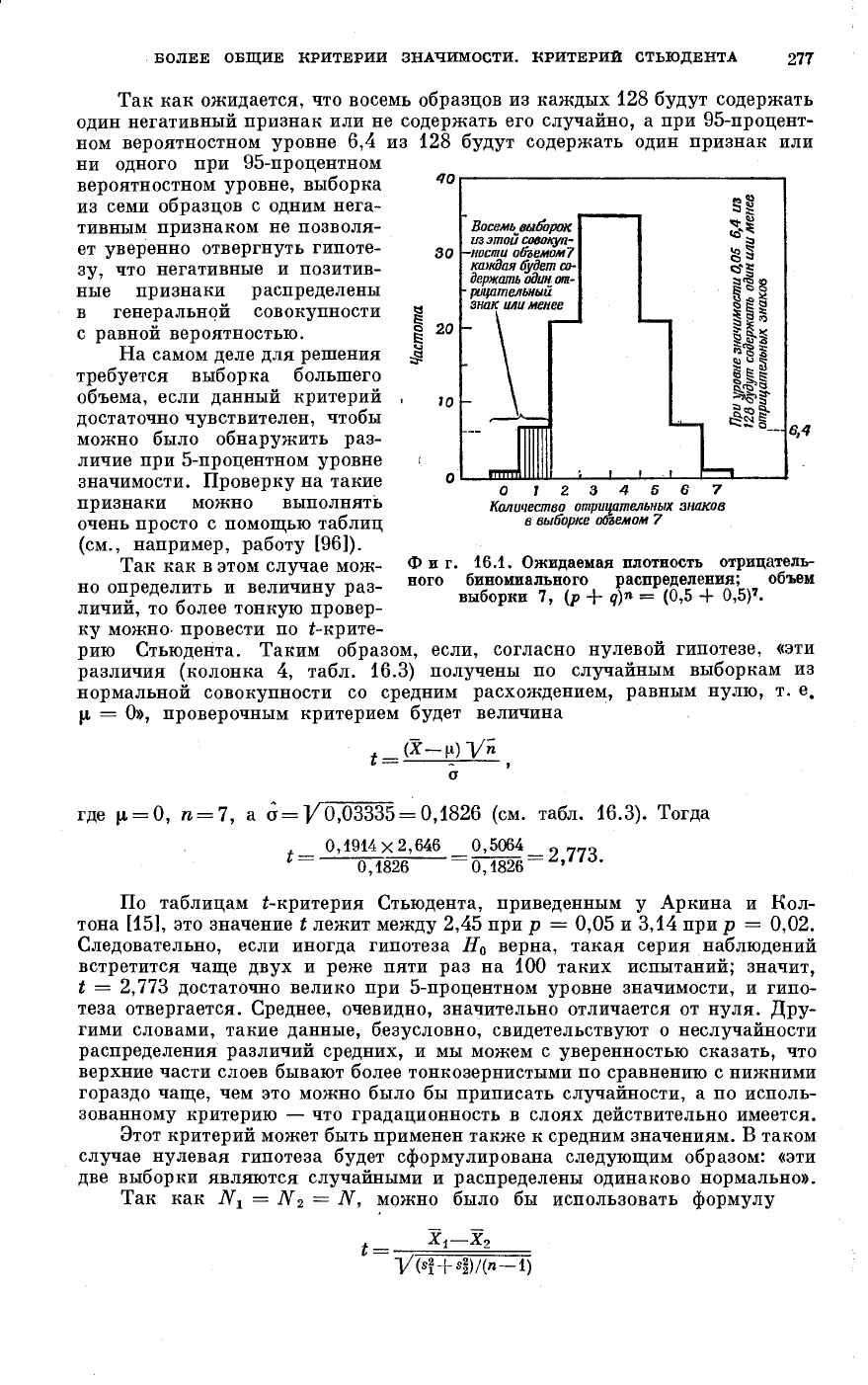
Таблица 16.2

Вероятности успеха (негативные признаки) при биномиальном

распределении с (р -f 9)

=(0,5 + 0,5) ч

Количество

негативных

признаков

Члены разложения бинома

ρΧ„Ν — X

JC I (JV —*

Χ) !

Частоты, ум-

ноженные на 128

(τ) (τ)

Ϊ28

(τ) (τ)

»(T)'(T)'-S

("2") ("2")

Ϊ28

(τ) ("2")

128

(τ) (τ)

128

Сумма

1,0

128

БОЛЕЕ ОБЩИЕ КРИТЕРИИ ЗНАЧИМОСТИ. КРИТЕРИЙ СТЬЮДЕНТА 277

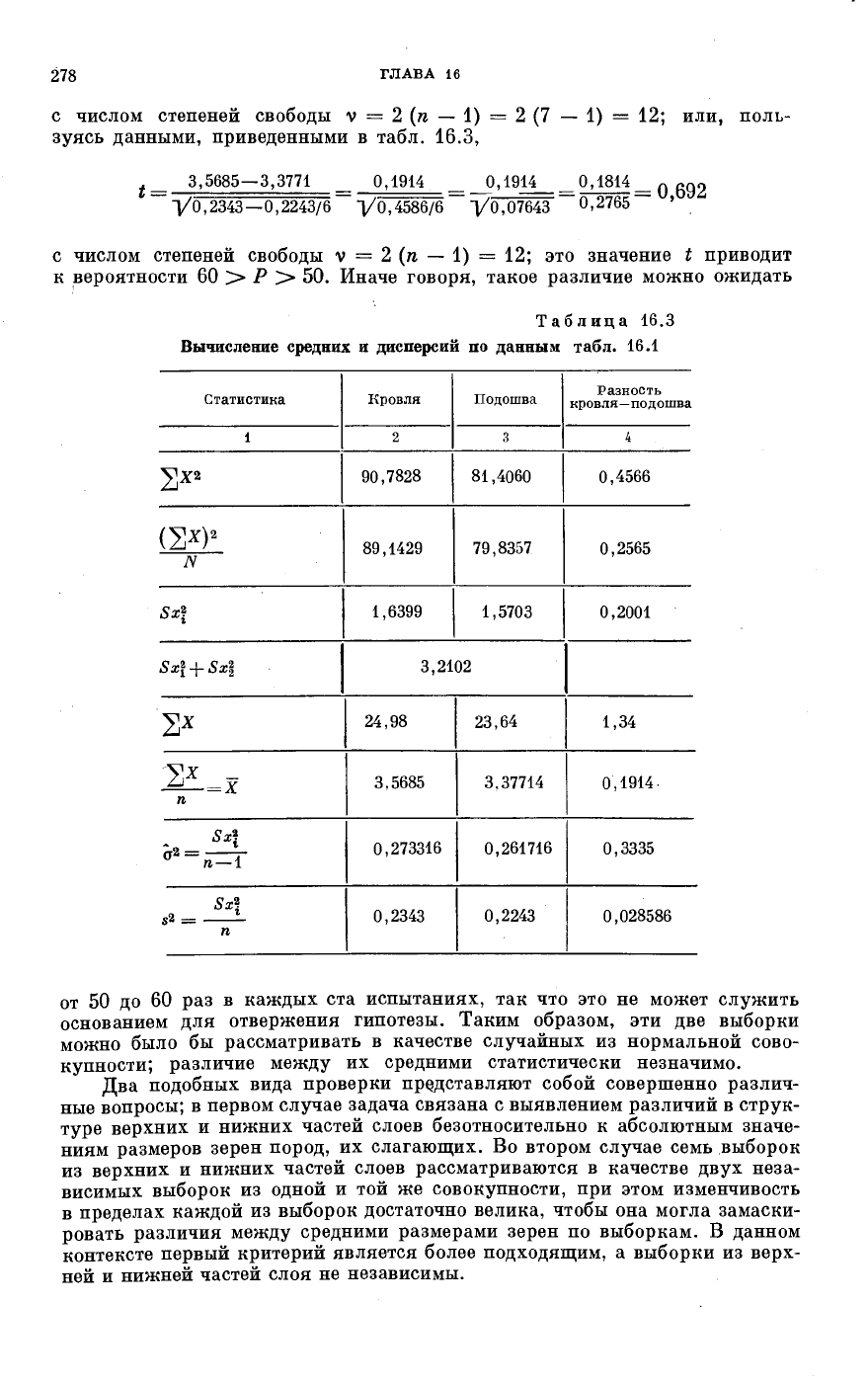
Так как ожидается, что восемь образцов из каждых 128 будут содержать

один негативный признак или не содержать его случайно, а при 95-процент-

ном вероятностном уровне 6,4 из 128 будут содержать один признак или

ни одного при 95-процентном

вероятностном уровне, выборка

из семи образцов с одним нега-

тивным признаком не позволя-

ет уверенно отвергнуть гипоте-

зу, что негативные и позитив-

ные признаки распределены

в генеральной совокупности

с равной вероятностью.

На самом деле для решения

требуется выборка большего

объема, если данный критерий

достаточно чувствителен, чтобы

можно было обнаружить раз-

личие при 5-процентном уровне

значимости. Проверку на такие

признаки можно выполнять

очень просто с помощью таблиц

(см., например, работу [96]).

Так как в этом случае мож-

но определить и величину раз-

личий, то более тонкую провер-

ку можно провести по ί-крите-

рию Стьюдента. Таким образом, если, согласно нулевой гипотезе, «эти

различия (колонка 4, табл. 16.3) получены по случайным выборкам из

нормальной совокупности со средним расхождением, равным нулю, т. е,

μ = 0», проверочным критерием будет величина

где μ = 0, re = 7, а σ = ]Λ),03335 = 0,1826 (см. табл. 16.3). Тогда

0,1914 x 2,646 _0,5064 Q

0,1826

—

0,1826 '

По таблицам ί-критерия Стьюдента, приведенным у Аркина и Кол-

тона [15], это значение t лежит между 2,45 при ρ = 0,05 и 3,14 при ρ = 0,02.

Следовательно, если иногда гипотеза H

верна, такая серия наблюдений

встретится чаще двух и реже пяти раз на 100 таких испытаний; значит,

t = 2,773 достаточно велико при 5-процентном уровне значимости, и гипо-

теза отвергается. Среднее, очевидно, значительно отличается от нуля. Дру-

гими словами, такие данные, безусловно, свидетельствуют о неслучайности

распределения различий средних, и мы можем с уверенностью сказать, что

верхние части слоев бывают более тонкозернистыми по сравнению с нижними

гораздо чаще, чем это можно было бы приписать случайности, а по исполь-

зованному критерию — что градационность в слоях действительно имеется.

Этот критерий может быть применен также к средним значениям. В таком

случае нулевая гипотеза будет сформулирована следующим образом: «эти

две выборки являются случайными и распределены одинаково нормально».

Так как N

= N

= N, можно было бы использовать формулу

^ Xi—X

ЙО

эо

ВосемьвыСюрок

из этой совокуп-

-иости объемом!

каждая будет со-

держать один от-

• рицательный

знак или менее

-L-

IIL

И;

ici-l

·» S S

IeI

111

О 12 3 4 5 6 7

Количество отрицательных знаков

в выборке объемом 7

Фиг. 16.1. Ожидаемая плотность отрицатель-

ного биномиального распределения; объем

выборки 7, (ρ + q)n = (0,5 + 0,5)

278

ГЛАВА 1 г

с числом степеней свободы ν = 2 (η — 1) = 2 (7 — 1) = 12; или, поль-

зуясь данными, приведенными в табл. 16.3,

3,5685—3,3771 _ 0,1914 _ 0,1914 _0,1814_

Q β92

~ 1/0,2343 —0,2243/6

У0,4586/6

У0,07643

0,2765

—

с числом степеней свободы ν = 2 (τι — 1) = 12; это значение t приводит

к вероятности 60 > P > 50. Иначе говоря, такое различие можно ожидать

Таблица 16.3

Вычисление средних и дисперсий по данным табл. 16.1

Статистика

Кровля Подошва

Разность

кровля—подошва

2 3 4

Σ*

90,7828

81,4060

0,4566

)

89,1429

79,8357

0,2565

Sx\

1,6399

1,5703

0,2001

Sxl

3,2102

Σ*

24,98 23,64

1,34

3,5685

3.37714 0,1914

Sx ι

= T

η—1

0,273316

0,261716

0,3335

Sx\

0,2343 0,2243 0,028586

от 50 до 60 раз в каждых ста испытаниях, так что это не может служить

основанием для отвержения гипотезы. Таким образом, эти две выборки

можно было бы рассматривать в качестве случайных из нормальной сово-

купности; различие между их средними статистически незначимо.

Два подобных вида проверки представляют собой совершенно различ-

ные вопросы; в первом случае задача связана с выявлением различий в струк-

туре верхних и нижних частей слоев безотносительно к абсолютным значе-

ниям размеров зерен пород, их слагающих. Во втором случае семь выборок

из верхних и нижних частей слоев рассматриваются в качестве двух неза-

висимых выборок из одной и той же совокупности, при этом изменчивость

в пределах каждой из выборок достаточно велика, чтобы она могла замаски-

ровать различия между средними размерами зерен по выборкам. В данном

контексте первый критерий является более подходящим, а выборки из верх-

ней и нижней частей слоя не независимы.

БОЛЕЕ ОБЩИЕ КРИТЕРИИ ЗНАЧИМОСТИ. КРИТЕРИЙ СТЬЮДЕНТА 279

16.7. ПРЕИМУЩЕСТВА ЭКСПЕРИМЕНТАЛЬНОГО РЕШЕНИЯ

Следует подчеркнуть контраст между этими двумя результатами; так,

во втором случае среднее различие было сравнимо с комбинированной оцен-

кой дисперсии из обеих выборок, а изменчивость в пределах выборок была

достаточно велика, чтобы она могла затушевать различия между средними.

Когда, однако, эти выборки были сведены попарно и каждую выборку

из верхней части слоя сравнили с соответствующей выборкой из нижней

части, мера изменчивости между этими двумя наборами наблюдений в зна-

чительной степени понизилась; иначе говоря, внутривыборочная изменчи-

вость по первому критерию стерлась. В общем можно рекомендовать исполь-

зовать выборки попарно; преимущества этого экспериментального решения

над вторым могут оказаться весьма значительными. Следует также заметить,

что число степеней свободы заметно возрастает от 6 в первом случае (спарен-

ные выборки) до 12 во втором. Если спаривание эффективно, сопровождаю-

щее его сокращение степеней свободы с лихвой компенсируется исчезнове-

нием изменчивости; но, если оказалось, что спаривание для ликвидации

внутрипластовой изменчивости неэффективно, попарное размещение при-

водит к уменьшению чувствительности f-критерия. Другой пример такой

процедуры описан Милнером [300]. Подобный аппарат известен под назва-

нием спаривание; это простой пример стратификации или блокирования,

и если изменчивость между слоями велика, а в пределах слоев мала, когда

данные упорядочены (стратификацией), эта классификация становится весьма

эффективной для получения более чувствительных статистических критериев.

Другое экспериментальное решение заключается в упорядочении по раз-

мерности (зерен). Выборки с равными размерами, даже неспаренные, обла-

дают определенным преимуществом; например, если вернемся к равен-

ству (16.15), O

= + п

)/п

, и вспомним, что t выражено фор-

мулой

t =

-¾

или t=

ΐ~

2 |/_gig2_

о У

(Ti

-Irn

) In

о у

+ п

увидим, что, если (X

-Z

фиксировано, значение будет меняться как

1 Z

+ п

Положим

= 0; тогда

/Ж= 1/1 = ^ = 2,236.

€ другой стороны, если

= 5 и га

= 15,

/Ж=/!=^

936

Другими словами, умножающий фактор и, следовательно, t будут наиболь-

шими при U

= п

. Такое различие более заметно для малых выборок. Рас-

сматривая такое экспериментальное упорядочение, Йоден [461] писал:

«Этим просто подтверждается установившееся мнение, что нет смысла опре-

делять очень точно одну из величин, если другая определяется со значитель-

ными ошибками».

Типпетт все же отметил другое преимущество: «Однако Уэлш [445]

показал, что, когда U

= п

, ί-критерий не чувствителен к различиям между

дисперсиями генеральной совокупности...» [430].

При внимательном подходе к подобному усовершенствованию упоря-

доченности экспериментов во многих случаях можно получить заметное

улучшение критериев как в практическом, так и в теоретическом отноше-

ниях.

280

ГЛАВА 1 г

16.8. ОЦЕНКА ОБЪЕМА ВЫБОРКИ, НЕОБХОДИМОГО

ДЛЯ ВЫЯВЛЕНИЯ СУЩЕСТВЕННОГО РАЗЛИЧИЯ

ПРИ ФИКСИРОВАННОЙ ВЕРОЯТНОСТИ

Другое преимущество ί-критерия Стьюдента состоит в том, что его можно

использовать для приближенного определения того объема выборки, кото-

рый необходим при установлении значимого различия между средними при

требуемом уровне значимости. Написав, что

(Χ

-μ)

' J

можно перестроить это выражение в другое:

, ί

'га = ^^ .

(х-μ)

При малой выборке возможно вычислить X и σ

, а зная число степеней

свободы и выбранный уровень значимости, найти t (и, следовательно, ί

);

еслй требуемое значение X — μ подставить в равенство (16.20), можно опре-

делить значение п.

В табл. 16.4 приведены данные пористости песчаников, определенной

двумя методами по двум выборкам.

Таблица 16.4

Сравнение методов измерения пористости [339]

Пористость, %

Образец различие

метод 1 метод 2

1 17,1 16,92

+0,18

2 20,1 20,68 -0,58

3 19,3

18,05

+1,25

10,2 10,39 —0,19

25,9 26,00 —0,10

Сумма

92,60

92,04

+0,56

Среднее 18,520

18,408

+0,112

Суммы квадратов SS

= 128,808 и SS

= 129,4311. Различие между

ними SS

= 1,9147. В последнем случае о^ = 1/^1,9147/« (η — 1) =

= Kl,9147/20 = 0,3094.

Положим, что, как и в вышеприведенных примерах, проверяется гипо-

теза H

, по которой эти различия получены из совокупности, где среднее

отличается от μ = 0. Тогда

или

с числом степеней свободы ν = τι — 1=4; тогда 80 > P > 70, иными

•

словами, для H

такое различие встретится от 70 до 80 раз на каждые 100 слу-

чаев, и нет оснований отрицать, что эти различия случайны и получены

БОЛЕЕ ОБЩИЕ КРИТЕРИИ ЗНАЧИМОСТИ. КРИТЕРИЙ СТЬЮДЕНТА 280

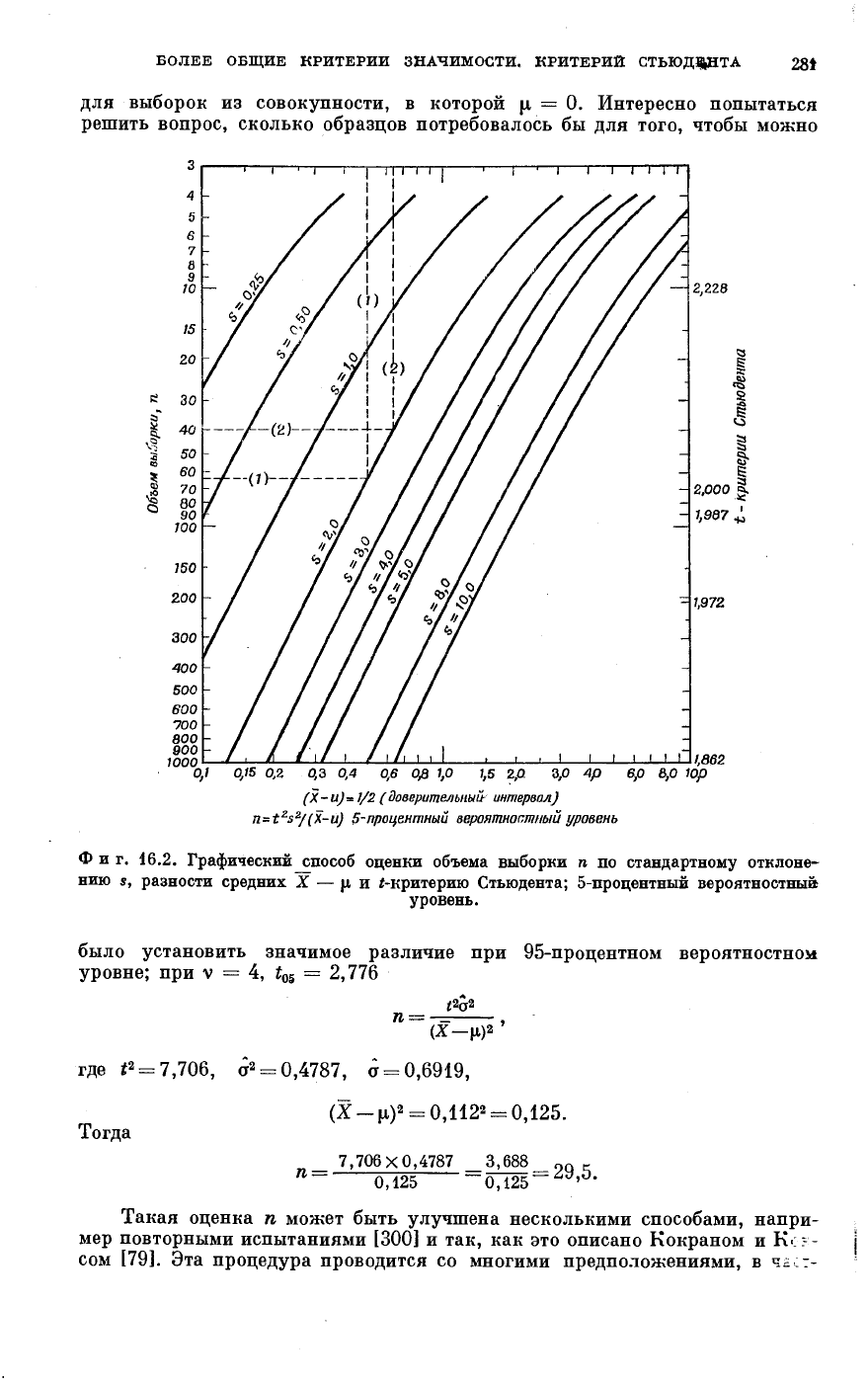
для выборок из совокупности, в которой μ = 0. Интересно попытаться

решить вопрос, сколько образцов потребовалось бы для того, чтобы можно

1000

0/5 0,2 0,3 0,4 0,6 Οβ 1,0 1,5 2,0 3,0 Ap

(X-uJ= 1/2 (доверительный- интервал)

n=t

/(X-u) 5-процентный вероятностный уровень

6,0 В, О юр

Фиг. 16.2. Графический ^способ оценки объема выборки η по стандартному отклоне-

нию s, разности средних X — μ и ί-критерию Стьюдента; 5-процентный вероятностный

уровень.

было установить значимое различие при 95-процентном вероятностном

уровне; при ν = 4, t

= 2,776

η-

(Χ-μΡ

где ί

= 7,706, σ

= 0,4787, σ = 0,6919,

(Χ

—

μ)

= 0,112

= 0,125.

Тогда

_ 7,706X0,4787 _ 3,688 _

- 0Д25 ~ 0,125

Такая оценка η может быть улучшена несколькими способами, напри-

мер повторными испытаниями [300] и так, как это описано Кокраном и Ко -

сом [79]. Эта процедура проводится со многими предположениями, в ч£,:т-