Гриффитс Дж. Научные методы исследования осадочных пород

Подождите немного. Документ загружается.

252

ГЛАВА 1 г

подбор функции распределения сам по себе еще не обладает большой ценно-

стью, за исключением удобства, получаемого при свертывании информации.

Второй момент заключается в том, что иногда следует построить, модель,

которая аппроксимирует наблюдаемое распределение; и, хотя серия полу-

ченных данных может отклоняться от модели, причина этого отклонения

объясняется, по-видимому, неслучайностью выборки. Конечно, можно уста-

новить такой способ отбора событий, при котором полученная система дан-

ных будет согласовываться с предложенной моделью; однако здесь снова

возникает неопределенность. Начинаем ли мы с выбора модели и по ней

определяем случайность выборки, или же начинаем с регулирования выбор-

ки и в предположении ее случайности ищем подходящую модель распреде-

ления, все равно дилемма эта возникает. Единственное ее решение, видимо,

заключается в следующем требовании: оба приближения должны сойтись

на некоторой конечной стадии аппроксимации.

Г Л А В А 15

Связь между средним и дисперсией

Как правило, когда при научных наблюдениях обнаруживают некон-

тролируемую изменчивость, значительно превышающую основную Maccg

наблюдений, удобно перед вычислением оценок их средних или дисперсий

переводить их значения в логарифмические·, в результате этого действия

повысилась бы точность оценок и изменения характера вытекающих из них

выводов.

J. Н. Gaddum, Lognormal Distribution, Nature, 156, p. 466

1945

15.1. ВВЕДЕНИЕ

После того как модель распределения результатов некоторого физиче-

ского (природного) процесса выбрана, необходимо оценить параметры этой

модели на основе собранных данных. Наиболее общий подход к проверке

пригодности модели обычно базируется на рассмотрении четырех первых

моментов (см. раздел 5.4). Затем необходимо изучить оценки параметров

с целью выяснить, независимы они или же как-то связаны.

Предположим, выбрана нормальная модель, которая определяется

двумя параметрами μ и σ

; о их значениях можно судить по соответствую-

щим выборочным оценкам — среднему X и выборочной дисперсии σ

. В слу-

чайной выборке из нормальной совокупности среднее не зависит от диспер-

сии, поэтому проверка их независимости является проверкой случайности

опробования.

Взаимоотношения между статистическими оценками могут определяться

различными причинами; например, в биномиальном распределении среднее

пр в известной мере зависит от дисперсии npq при использовании как пара-

метров, так и оценочных функций; но, если оценки получены не по данным

случайной выборки, взаимоотношения могут отличаться от ожидаемых.

Опять же, поскольку ожидаемое поведение параметров может быть посту-

лировано на основании Ьвойств модели, процедура измерения может искус-

ственно вызвать смещение, которое приведет к иным взаимоотношениям

рассматриваемых параметров. Поэтому изучение взаимоотношений между

оценками представляет существенный интерес в качестве проверки выпол-

нения условий модели. Без этого не обойтись не только вследствие необхо-

димости выявить экспериментальные трудности (определяющие причины),

но также вследствие необходимости избрать такую аналитическую про-

цедуру, чтобы ее требования выполнялись в последующем статистическом

анализе Преобразования выбирают так, чтобы можно было получить

характеристики с нужными свойствами для проверки гипотез и обеспечить

В частности, например, следует убедиться, что дисперсии однородны, постоянны

и аддитивны.

254

ГЛАВА 1 г

надежность вероятностных утверждений, на основании которых делаются

выводы.

В общем процедуру измерений, которая ведет к данным «естественной»

шкалы, невозможно выбрать a priori, и поэтому единицы измерения выби-

рают главным образом из соображений условности и удобства. Преобразова-

ния можно затем рассматривать как служащие целям эффективного контроля

данных, получаемых в результате измерений. Довольно часто, например,

«природа» «оперирует» геометрической шкалой и измерения, выполненные

по арифметической шкале, оказываются трудоемкими в работе; если же

измерения преобразовать в логарифмическую шкалу, переменные могут под-

чиняться нормальному закону или какой-либо другой из известных функ-

ций распределения [227]. Маловероятно, что шкалы, которые мы избираем

для классификации данных, являются ab initio, т. е. «лучшими», так что

трансформация представляет собой весьма общую процедуру [138].

Изучение взаимоотношений между оценками представляет, кроме того,

интерес как для достижения требований теоретической модели, так и для

понимания физического смысла изменений изучаемой величины.

15.2. ВЗАИМООТНОШЕНИЯ СРЕДНЕГО PI ДИСПЕРСИИ В МОДЕЛЯХ

Выше упоминалось, что если модель определена, то взаимоотношения

между средним μ и дисперсией σ

или средним μ и стандартным отклонением

σ также в общем должны быть известными. Среднее μ не зависит от диспер-

сии σ

в случайных выборках из нормально распределенной совокупности.

При нормальном распределении выборки не случайны, если выборочное

среднее X связано с выборочной дисперсией о

. Для параметрического ста-

тистического анализа необходимо повторять и изменять отбор до тех пор,

пока не будет достигнута случайность выборки, изменять процедуру так,

чтобы исчезло смещение или же применять соответствующее преобразование

(см. следующий раздел), чтобы можно было убедиться в независимости сред-

него от дисперсии.

При использовании дискретной шкалы и биномиальной модели среднее

μ зависит от σ

, ибо μ = пр, а σ

= npq. Можно видеть, что дисперсия воз-

растает вместе с возрастанием ρ от 0 до 50 единиц и затем симметрично убы-

вает от 50 до 100 единиц (см. табл. 10.3); таким образом, максимальное зна-

чение дисперсии равно 50. Когда шкала пропорционально изменена путем

деления на η или переведена в процентную делением на и и умножением

на 100, дисперсия становится минимальной при значении 50 и симметрично

возрастает в обе стороны от этого значения. Если по системе выборочных

данных станут известны эти взаимоотношения и если мы собираемся исполь-

зовать, скажем, дисперсионный анализ, то необходима трансформация изме-

рений в такую шкалу, по которой среднее стало бы независимым от дисперсии

([22] и табл. 15.1).

В распределении Пуассона μ = пр и σ

= пр; таким образом, дисперсия

возрастает вместе со средним; поэтому при параметрическом анализе, выпол-

няемом по данным, согласующимся с функцией распределения Пуассона,

требуются преобразования в такую шкалу, в которой среднее независимо

от дисперсии ([22] и табл. 15.1).

У большинства функций распределения, обладающих асимметрией,

среднее так или иначе связано с дисперсией; аналогично, если эксцесс зна-

чителен, в последующих сравнениях среднего и дисперсии отражается влия-

ние «дисперсии дисперсии». Очень часто, когда среднее и дисперсия связаны,

выборочные данные имеют дисперсию, существенно зависящую от другой

случайной величины; а в тех данных, которые обладают дисперсией, возра-

стающей вместе с возрастанием среднего или уменьшающейся при возраста-

нии среднего, дисперсия гетерогенна. Это является серьезной причиной неко-

СВЯЗЬ МЕЖДУ СРЕДНИМ И ДИСПЕРСИЕЙ

255

торых неудач статистического анализа, основанного на двухмерных дан-

ных (см., например, работы [169, 181]).

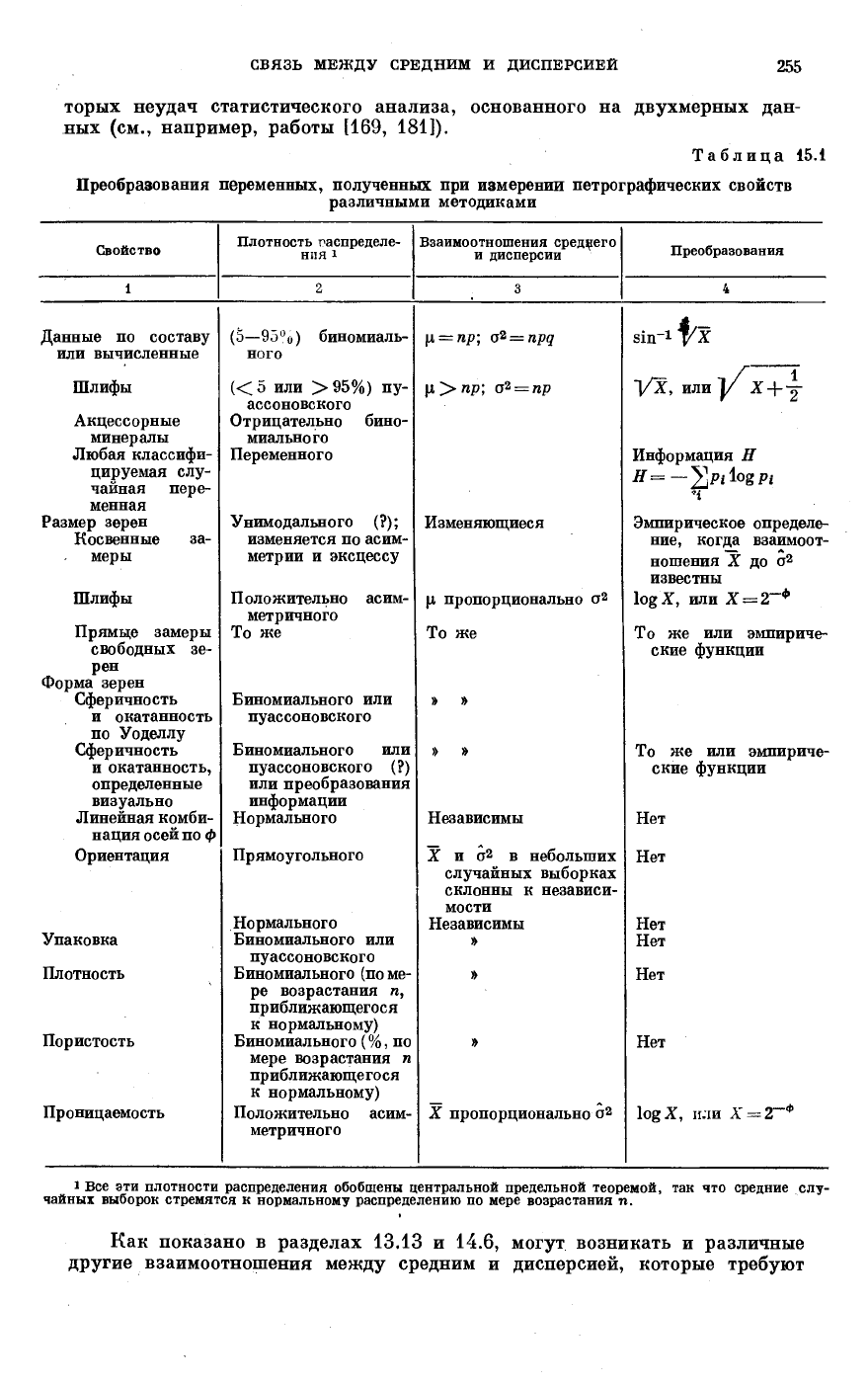
Таблица 15.1

Преобразования переменных, полученных при измерении петрографических свойств

различными методиками

Свойство

Плотность распределе-

ния ι

Взаимоотношения среднего

и дисперсии

Преобразования

3 4

Данные по составу

или вычисленные

Шлифы

Акцессорные

минералы

Любая классифи-

цируемая слу-

чайная пере-

менная

Размер зерен

Косвенные за-

меры

Шлифы

Прямще замеры

свободных зе-

рен

Форма зерен

Сферичность

и окатанность

по Уоделлу

Сферичность

и окатанность,

определенные

визуально

Линейная комби-

нация осей по φ

Ориентация

Упаковка

Плотность

Пористость

Проницаемость

(5—95 °о) биномиаль-

ного

«5 или >95%) пу-

ассоновского

Отрицательно бино-

миального

Переменного

Унимодального (?);

изменяется по асим-

метрии и эксцессу

Положительно асим-

метричного

То же

Биномиального или

пуассоновского

Биномиального или

пуассоновского (?)

или преобразования

информации

Нормального

Прямоугольного

Нормального

Биномиального или

пуассоновского

Биномиального (поме-

ре возрастания п,

приближающегося

к нормальному)

Биномиального (%, по

мере возрастания η

приближающегося

к нормальному)

Положительно асим-

метричного

= ηρ; а

= прд

μ > пр; σ

= пр

Изменяющиеся

μ пропорционально σ

То же

» »

D »

Независимы

X и σ

в небольших

случайных выборках

склонны к независи-

мости

Независимы

X пропорционально σ

sin-1 j/x

УХ, или j/~X + Y

Информация H

H = -^

1о

Эмпирическое определе-

ние, когда взаимоот-

ношения X до σ

известны

IogZ, или Х = 2Г*

То же или эмпириче-

ские функции

То же или эмпириче-

ские функции

Нет

IogZ, или

А"

= 2

ι Все эти плотности распределения обобщены центральной предельной теоремой, так что средние слу-

чайных выборок стремятся к нормальному распределению по мере возрастания п.

Как показано в разделах 13.13 и 14.6, могут возникать и различные

другие взаимоотношения между средним и дисперсией, которые требуют

256 ГЛАВА 1 г

некоторых стабилизирующих преобразований. В общем случае, когда это

достижимо, определенная экспериментальная процедура может быть при-

ведена в соответствие с подходящей моделью распределения путем модифи-

кации процедуры отбора. Когда экспериментальные данные собраны,

а функция распределения еще не известна, рекомендуется рассмотреть раз-

личные статистические критерии с целью-выявить малейшую степень зави-

симости между средним и дисперсией. Если появляются признаки этой зави-

симости, следует предпринять меры по изменению экспериментальной про-

цедуры или применить преобразования, чтобы, насколько это возможно,

подчинить исходные данные тем требованиям модели, которые входят в ис-

пользуемые статистические оценки. Предположения, лежащие в основе

процедуры дисперсионного анализа, детально рассмотрены Эйзенхартом

1109]; о влиянии расхождений на результаты оценивания писал Кокран

175], а Бартлетт [22] установил и рассмотрел те преобразования, которые

могут быть использованы в случаях, когда собранные данные оказываются

выраженными в форме, не подходящей для дисперсионного анализа.

15.3. ПРЕОБРАЗОВАНИЯ, ПОЗВОЛЯЮЩИЕ ДОСТИГНУТЬ

НЕЗАВИСИМОСТИ СРЕДНЕГО АРИФМЕТИЧЕСКОГО X

И ВЫБОРОЧНОЙ ДИСПЕРСИИ о

Если распределение известно, а используемая выборка действительно

случайна, взаимоотношения между μ и о

можно выразить в постулирован-

ном виде. Для тех видов распределения, в которых взаимоотношения между

μ и о

принимают известные формы, нужные преобразования установлены

теоретически. Перечень таких преобразований для обычных моделей при-

водится в табл. 15.1, аналогичный перечень табулирован Крамбейном

и Миллером [260], Крамбейном [261], а также Миллером и Каном [299].

Таблицы, облегчающие подобные преобразования, приводятся в работах

[128] и [409]. В табл. 15.1 включены такие распределения, которые ожи-

даются для случайного опробования геологических совокупностей с исполь-

зованием процедур измерений, описанных в предыдущих главах (см. также

работу [261]). Например, если надлежащим способом опробована совокуп-

ность стратифицированных образований, скажем слоев обломочных осадоч-

ных пород, с использованием таких единиц, как пласт, и если из образцов

выбраны зерна кварца с целью определения их устойчивых характеристик,

то логарифмы длинных осей кварцевых зерен, замеренных непосредствен-

ным способом, как это описано в разделе 4.10, окажутся нормально рас-

пределенными. Может, конечно, произойти смещение вследствие различных

отклонений от рекомендованной процедуры анализа, и в общем случае,

если будет это смещение, частотная функция измерений осей кварцевых

зерен также соответственно отклонится от нормальной модели. В частности,

заметим, что почти наверняка возникнут некоторые связи между выбороч-

ным средним X и выборочной дисперсией σ

. Поэтому проблема проверки

утверждения, что данные измерений собраны надлежащим образом, не столь

уж тривиальна.

Когда исходный материал собран, а функция распределения еще не

известна и при этом появились признаки зависимости между X π σ

, необ-

ходимо подобрать форму преобразований для перевода данных в такую

шкалу, в которой X независимо от σ

. Бартлетт [22] рекомендует следую-

щую процедуру. Предположим, что дисперсия σ

представляет некоторую

функцию / от среднего πι, т. е. σ

= / (т)\ тогда для любой функции g (χ)

выполняется приближенное равенство: = J (dg/dm)* f (τη).

СВЯЗЬ МЕЖДУ СРЕДНИМ И ДИСПЕРСИЕЙ

257

Если дисперсия постоянна, например С

, то

Предположим далее, что / (т) пропорционально т

, тогда аппроксими-

рующее преобразование будет g (т) = log т. Пример применения такой

процедуры дан Розенфельдом и Гриффитсом [363]. Если применена эмпири-

ческая процедура такого рода, следует учесть, что данное преобразование,

полезное для материалов, на которых оно основано, может оказаться непри-

менимым за пределами данной ситуации. Так, в приведенном выше примере

[363] значение окатанности более чем 0,7 единицы дает отрицательное значе-

ние, поэтому данное преобразование нельзя считать подходящим для всех

случаев изучения окатанности.

Множество взаимоотношений между средним X и дисперсией σ

или

стандартным отклонением изображено графически в работе [340] с рекомен-

дациями для соответствующих преобразований; этими взаимоотношениями

довольно часто (см. ниже) приходится пользоваться для понимания при-

роды изменений случайной переменной и (или) для выяснения причины сме-

щения.

15.4. ПРИМЕРЫ РЕАЛЬНО СУЩЕСТВУЮЩИХ СВЯЗЕЙ

МЕЖДУ ОЦЕНКАМИ

15.4.1. Размеры зерен и сортировка по размерам

Средние размеры зерен и характер распределения (дисперсия) этих

размеров представляет значительный интерес для геологических исследова-

ний, так как часто полагают, что размер зерен отражает местные условия

седиментации, такие, например, как скорость течения (см. раздел 13.12).

Дисперсия размеров зерен в общем случае выражает отсортированность

(мера однородности по размерам зерен) и рассматривается как возможность

типизировать определенные геологические процессы; например, эоловые

пески хорошо отсортированы, а флювиогляциальные — плохо, что соот-

ветственно отражает разницу в характере деятельности ветра и льда и что

сказывается на. размерности переносимого материала. Если распределение

случайной величины, характеризующей размеры зерен, нормально, то сред-

нее X и выборочная дисперсия а

или стандартное отклонение σ отражают

средний размер и отсортированность по размерам; но если распределение

ненормально, на меру сортировки будут влиять различные другие оценки;

в частности, важное значение приобретает эксцесс. У наиболее хорошо

отсортированных осадков зерна одинакового размера; в этом случае при

любом измерении одновременно получают и среднее значение; дисперсия

в этом случае равна нулю. Если же есть хотя бы небольшое различие в раз-

мерах зерен, дисперсия становится отличной от нуля, а эксцесс — беско-

нечно большим. Поэтому в случае отклонения распределения от нормаль-

ного оценивать отсортированность по размеру зерен надо осторожно.

Другая весьма интересная черта процедуры измерения размеров зерен

состоит в том, что различная методика приводит к различным результатам

(гл. 3) и, в частности, к различным связям между средним X и дисперсией

или соответственно между размерами и степенью отсортированное™.

Связь между размерами зерен и степенью их отсортированности при кос-

венных измерениях. Если размеры зерен определяются не прямыми измере-

ниями, например путем просеивания или прокапывания, наблюдаемая кри-

вая распределения будет открытой в области крайних значений (см. раздел

5.2); в таких случаях для оценки среднего μ и стандартного отклонения σ,

17-429

258

ГЛАВА 1 г

надо использовать такие статистики, как медиана Μά

, полуразмах кварти-

ля QD

или полуразмах квантиля РБ

. Обычно обнаруживается, что между

медианой и оценкой дисперсии существует связь [150, 213, 394]. Эта тен-

денция может трактоваться как линейная по отношению к некоторому диа-

пазону размеров зерен (см., например, работу [150]), но она оказывается

нелинейной для всего ряда размеров [150, 151]. Этот весь ряд не представ-

ляется адекватно, по-видимому, вследствие систематической ошибки опро-

бования (см. раздел 5.6), но по опубликованным данным можно вывести

гипотетические связи для ряда от —6 до 14<£(от 64 мм до 0,06 мк), что пока-

зано на фиг. 15.1. Если генеральная совокупность рассматривается в целом,

то медиана значений размеров зерен окажется независимой от дисперсии

Волочение Сальтация Суспензия

< > < >

64000

16 OOC

4 000 IOOO ZSО 625 15,6 3,9 0,95 0,24 Cfiet

Медианный

диаметр, McL

Фиг. 15.1. Размеры Мс1

и отсортнрованность по размерам PD

ljl

в обломочных осадках;;

косвенная процедура измерений.

в единицах ф, как это можно было бы ожидать по случайному опробованию

нормальной совокупности (см. фиг. 5.4 и раздел 5.6). Эту общую законо-

мерность можно выразить двумя горбообразными кривыми на основании

характеристик транспортируемой среды; размеры от 4 до 14 φ (от 62,5 мм

до 0,06 мк) отражают тонкозернистый обломочный материал, который пере-

носится в виде суспензий, в то время как в интервал от 2 до —6 φ (от 250 мк

до 64 мм) входит грубозернистый материал, транспортируемый волочением.

Эти два вида переноса перекрываются в области от 2 до 4 ψ (от 250 мк до

62,5 мм)·, частицы такого размера переносятся уже сальтацией. Такую

закономерность можно подразделить и далее — на тройные серии при исполь-

зовании сортирующих характеристик различных сред; наиболее тонкая

сортировка материала происходит в результате эоловых процессов (дюнные

пески и лёссы), при этом дюнные пески переносятся путем сальтации, а лёссы

образуются за счет переноса в виде суспензий. По-видимому, примеров

эолового детрита, который отвечал бы по размерам интервалу от 1,5 до 6 ψ-·

единиц (от 35 до 15,6 мк), наберется не много.

Обломочный материал субаквального происхождения можно классифи-

цировать аналогично. Наиболее плохо отсортированные осадки характери-

зуют ледниковые и гравитационные процессы седиментации. Не совсем чет-

кий характер этой закономерности в основном объясняется недостаточным

количеством информации по распределению размеров частиц в подобных.

отложениях.

СВЯЗЬ МЕЖДУ СРЕДНИМ И ДИСПЕРСИЕЙ

259

Наиболее хорошо отсортированные осадки соответствуют областям

около 3,4 φ (95 мк), 2,8 φ (144 мк) и 2,2 φ (218 мк), т. е. трем различным сре-

дам отложения. Как и следовало ожидать, агенты переноса и их транспор-

тирующие характеристики действуют как процессы неслучайного отбора,

они приводят к различной степени асимметрии распределения, которая отра-

жает интенсивность селективной, сортировки при каждом процессе.

Теперь рассмотрим асимметрию и эксцесс, измеренные надлежащим

способом и определенные [250, 248] как

(15.2)

(15.3)

Можно видеть, что эти линейные функции имеют одни и те же параме-

тры — медианы, квартили и квантили — размеров (медиана) и отсортиро-

ванное™ (QD

)

и РБф); поэтому они не могут быть независимыми, и в по-

строении этих статистик более высокого порядка мало смысла вследствие

того, что результат их можно предсказать по взаимоотношению между медиа-

ной и оценкой дисперсии.

Возвращаясь к графику отсортированности, представленному на

фиг. 15.1, и рассматривая плотность распределения выборок, в которых

наблюдается приведенная закономерность, заметим

(

что данная функция

при Значениях около —6ф, от 2 до 4фп от 12 до 14ф, склонна к симметрич-

ности и по крайней мере приближается по форме к нормальной кривой. Во

всех этих трех областях значений обломочный материал становится

монодисперсным, т. е. мономинеральным; например, галька, при осажде-

нии ведущая себя одинаково, в области —6ф, кварцевые зерна в интервале

от 2 до 4ф и вид глинистых минералов, представляющий интервал от 12 до

14ф-единиц. Если начать с типичного песка, сложенного кварцем при сред-

нем размере зерен (медиана), равном 3ф, и последовательно и постепенно

увеличивать в нем количество глинистых минералов, частотная кривая

будет все более отклоняться от симметричного вида, т. е. в первую очередь

увеличится асимметрия. В конце же асимметрия уменьшится, кривая снова

станет симметричной в области, соответствующей осаждению из воды в виде

суспензии; если же продолжать добавлять глинистые минералы, знак асим-

метрии, которая станет возрастать и затем вновь уменьшаться, изменится

кривая будет опять симметричной (нормальной) близ значения 12ф. Анало-

гичные изменения симметрии кривой происходят в интервале от 2 до —6ф-

единиц при последовательном увеличении в кварцевом песке содержания

«гравия» (обломков пород). Изменения асимметрии кривой с добавлением

к песку гравия или глины сопровождаются изменениями минерального соста-

ва, размеров зерен, облика породы; следовательно, изменения так называе-

мой размерной частотной функции действительно отражают изменения трех

независимых переменных, как и описано в гл. 3.

Нет смысла дальше разъяснять как, используя модель, можно предска-

зывать взаимоотношения в пределах всего ряда кластических осадков;

а попытки интерпретировать «значение» плотности распределения размеров

частиц пород не смогут преодолеть путаницу в изменениях, которые зависят

от трех различных причин. Действительно, это не будет истинной величиной

измерения; изменение описанных статистик отражает лишь ту величину,

о которой было сказано в гл. 3 и 4. Размерность верен в общем не может

быть связана исключительно с характеристиками транспортирующей среды

Это отношение взято обратным выражению, которое привел Крамбейн, чтобы воз-

растающие значения эксцесса отражали возрастание пикообразности.

17*

Sbb=Mf-**L

„ . .2(^90 + ^10)

260

ГЛАВА 1 г

вследствие полигениости кластического материала, поэтому строгий мате-

матический анализ здесь неприменим. Процедура измерения размеров зерен

и их обработка в лучшем случае может привести лишь к выводам о порядке

полученных данных.

Связь между размерами зерен и их отсортированностъю по размерам

(наблюдения в шлифах). При измерениях кварцевых зерен в шлифах (а —

длинная ось, Ъ — короткая), как это рекомендовалось в разделе 6.3.1, опять

же применяется ф-нормальная функция распределения. Следовательно,

можно было бы ожидать, что, если выборка случайна, средний размер зерен,

представленный в данном случае выборочным средним Х

, и отсортирован-

ность, выржаемая выборочным стандартным отклонением σ

, будут незави-

симы друг от друга Мерой линейной зависимости здесь может быть коэффи-

Таблица 15.2

Взаимоотношения между размером и размерностью сортировки σ

определенной как корреляционный коэффициент г; использованы

измерения осей кварцевых зерен из песчаника Мэкстон, Западная

Виргиния; измерения выполнены по шлифам

Статистики

"α

°ъ

σ&

+0,993 **

-0,263

-0,276

-0,255

-0,280

+0,724 **

Примечание. Для а — длинная ось, Ф-единицы;

для

— короткая ось, Ф-единицы;

η — 33 шлифа; г > 0,349 *;

г> 0,449 **.

циент корреляции (см. раздел 21.12), пример дан в табл. 15.2,· где используют-

ся данные измерений осей кварцевых зерен в шлифах из миссисипских песков

Мэкстон, Западная Виргиния.

Сходные результаты получены при аналогичной обработке других

песчаниковых отложений, например песчаников Солт-Уош [164], Кау-Ран

[167], Чипмунк [410, 319], Уэйнсберг и Мидл-Киттаннинг [399] и кварцитов

Туг.карора, Орискани и· Хомвуд [457]. Следовательно, при изучении разме-

ров кварцевых зерен по их осям в шлифах можно убедиться в том, что сред-

нее обычно не зависит от стандартного отклонения. При некоторых таких

исследованиях в результате обработки наблюдений слабую зависимость

можно принять за значительную, но, если учесть, что коэффициент опреде-

ленности г

(см. раздел 21.2), выраженный в процентах, редко превышает

10% или он не более 10% изменчивости размеров осей кварцевых зерен, что

обычно для среднего и стандартного отклонения, этой ошибки не произойдет.

В табл. 15.2 перечислены стандартные отклонения для случая, когда.коэф-

фициент корреляции для той или другой пары осей значителен, что наблю-

дается при слабой линейной зависимости между этими парами, вызванной

плохой методикой составления выборки (чему подвержены 5% подобных

исследований) или же неслучайностью самого процесса отбора проб.

Рассмотрим в качестве примера процедуру измерения осей «кварцевых»

зерен в шлифах из образцов кварцитов Потсвилл и Тускарора (восточная

Пенсильвания) [273].

Область значений σ — от 0,25 до 1,5 ф-единиц; см. разделы 5.7 и 17.6.

СВЯЗЬ МЕЖДУ СРЕДНИМ И ДИСПЕРСИЕЙ 261

Результаты изучения 54 образцов кварцитов Потсвилл показали, что среднее

и дисперсия значений размеров длинных осей кварцевых зерен независимы.

По 46 образцам из формации Тускарора был подсчитан порядковый коэффи-

циент корреляции φ

[341 ]

между средним размером Х

и стандартным откло-

нением 0ф длинных осей, что дало значительную величину ф

= —0,409 (для

η = 46, при 5-процентном уровне значимости) [341]. На этом основании

можно допустить, что около 16% изменчивости этих двух критериев общие,

а 84% независимы.

Если этот коэффициент корреляции реален, то дисперсия должна воз-

растать по мере увеличения значения среднего φ или увеличения среднего

размера зерен (фиг. 15.2); другими словами, тенденция к.огрублению зерни-

стости «кварца» значительно сильнее тенденции к уменьшению зернистости.

Однако эта зависимость хотя и существенна, но все же мала и может быть

отражением пристрастного отбора.

Зависимость между размерами зерен и их отсортированностъю при пря-

мых измерениях отдельных зерен. Снова возьмем ф-нормальную модель

7,0 τ-

Ο,8 -

а* °'

; * р

0,4 - , V

** х

.А

0,2

φ-0,409*

.χ

"χ* X X

*χ

X X

Φ в г. 15.2. Размеры Аф по отношению к сор-

тировке σφ по длинным осям кварцевых зерен

из кварцитов Тускарора [273].

?>°

>° 3ρ 4,0

Χ,

φ-единицы

функции распределения и предположим, что в случайной выборке среднее

независимо от дисперсии. Такие предположения подтверждаются на немного-

численных материалах, которйми являются, например, кварц из тяжелых

и дюнных песков [204], кварцитовая галька из гравия Нью-Джерси [411, 412],

обломки кварцитов из осыпей формации Тускарора, кварцитовая галька

конгломератов Олиан и кварцитовые зерна из кварцитов Хомвуд [169, 181].

Детальное изучение изменений размеров и формы зерен кварца, граната и ро-

говой обманки из пляжных, дельтовых и ледниковых отложений плейстоцена

Онтарио (Канада) описано Мак-Интайром [295]; здесь нет какой-либо явной

закономерности, и для 5-процентного уровня линейная зависимость среднего

и дисперсии, оцененная коэффициентом корреляции среднего φ (ф

= —0,288, η = 81) не очень значительна [341]. Даже если это значение

и существенно, общая изменчивость для средней и дисперсии должна была

бы быть менее 10%. Здесь стандартное отклонение снова имеет очень ограни-

ченный размах, аналогичный тому, который получается при изучении шли-

фов, где значение σ изменяется от 0,2 до 1,0ф -единиц.

15.4.2. Форма частиц в осадках

и их отсортированность по форме

Взаимоотношения между средним X и дисперсией σ

сферичности и ока-

танности кварцевых зерен в обломочных отложениях описаны в гл. 6.1. Если

процедуру измерения этих параметров производить визуально, то зависимо-

сти по сферичности можно и не заметить, но зависимость по окатанности

заметить можно. Набор данных в этой области для какого-либо обобщения

очень ограничен; исследователи же области распределения окатанности

обычно сильно склоняются к малым ее значениям. Необходимы какие-то

преобразования, но предложить общие рекомендации пока трудно.