Гриффитс Дж. Научные методы исследования осадочных пород

Подождите немного. Документ загружается.

222

ГЛАВА 1 г

Таблица 13.4

Площади, ограниченные кривой

нормального распределения

в определенных границах

Предел

Площадь, %

μ+σ

67,45

μ±2σ 95,45

μ+3σ

99,73

μ+4σ

99,994

личением η уточнить данные об интервале, в котором лежит X, настолько,

насколько нам это нужно, или по крайней мере насколько возможно.

Рассмотрим распределение медиан на фиг. 5.4. Среднее X, являющееся

оценкой для μ, равно 3,34ф, а выборочное стандартное отклонение σ = 2,44.

Тогда, замещая X на μ и σ на σ, можно заключить, что большая часть зна-

чений попадает в интервалы, данные в табл. 13.5.

Таблица 13.5

μ±ίίσ

Медиана, %

0,90-5,78 67,45

-1,54-8,22 95,45

3 —3,98—10,66

99,994

Если мы возьмем выборки и подсчитаем среднее для каждых четырех

образцов, то область значений можно будет выразить как μ + ka/Yn, что,

как известно, позволяет сузить интервал наполовину; увеличением же коли-

чества наблюдений, по которым вычисляется среднее, можно будет эффек-

тивно уменьшить этот интервал до любых пределов. Стоимость такой про-

цедуры быстро возрастет с увеличением п; так, среднее, вычисленное по выбор-

ке объемом η = 16, уменьшает интервал только до V

его первоначального

значения.

Из другого примера известно, что функция распределения случайной

величины Xt, где X

— сферичность, по Крамбейну, близка к нормальной

со средним μ = 0,75 и стандартным отклонением σ = 0,08 (см. фиг. 6.13

и соответствующий текст), и мы измеряем сферичность по небольшой выборке,

равной всего 16 кварцевым зернам, дающей X = 0,68; когда эта выборка

случайна, можно предсказать, что три из 1000 таких проб окажутся в среднем

за пределами -границ μ± 3alYn, или 0,75 + 0,06, или от 0,69 до 0,81. Пре-

дыдущие опыты не оставляют сомнений в нормальности распределения, так

что неверно именно предположение о случайности распределения. Действи-

тельно, мы ожидаем, что естественные процессы сортировки зерен по их форме

скорее всего не случайны, так что процесс, обусловивший среднюю сфе-

ричность данной выборки, равную 0,68, привел также к скоплению зерен

с необычайно низкой сферичностью. Средняя сферичность аркозов равна

0,733 по выборке в 900 проб (Yn = 30); тогда, используя оценки по большой

выборке в качестве параметров совокупности, мы вправе ожидать, что

три из 1000 проб будут иметь сферичность за пределами интервала 0,75 ±

+ 0,008, или за пределами интервала 0,742—0,758. Следовательно, аркозы

ПЛОТНОСТЬ РАСПРЕ ДЕЛЕ HHH

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

223

обладают меньшей сферичностью по сравнению с тем, что можно было бы

предположить по случайным выборкам такого же объема, отобранным из

определенной совокупности проб.

13.8. ПОНЯТИЕ О ДОВЕРИТЕЛЬНОМ ИНТЕРВАЛЕ

Теперь можно использовать характеристики нормального распределе-

ния с целью выработать вероятностные суждения о случайной величине

в предположении, что она непрерывна.

Вероятно, следует подчеркнуть, ЧТО ПО T^i Доверительный

одному эксперименту нельзя ничего утвер- I J

mme

eaл

ждать. На последнее мы имеем право

только в том случае, когда эксперимент

повторен множество раз. Можно исполь-

зовать следующее свойство нормального

распределения: средние значения, полу-

ченные по случайным выборкам из нор-

мальной совокупности со средним μ и

стандартным отклонением σ, могут сами

ф и г

· Доверительный интер-

быть распределены нормально со сред-

вал и 6Г

Г°

ним μ и стандартным отклонением σ/j/rc.

По данным таблицы нормального распределения можно !утверждать, что

95% этой площади соответствует интервалу μ + 1,96σ; отсюда X — μ попа-

дет в интервал μ +

,96а/Уга в среднем в 95% случаев. Выразив это нера-

венством, получим

1,96σ Ι-

<μ —Х<-'

I I

I ι

У η У η

или, прибавив X к каждой части неравенства,

-^-<

<Ζ-

1 1,96σ

Уге

' У η

Предположим, например, что мы работаем со случайной величиной X

которая представляет собой замеры длинных осей кварцевых зерен и выра-

жается их логарифмом. Допустим, что на базе очень большой выборки мы

получили практически точную оценку σ = 0,5 φ. Выборка в га = 25 заме-

ров дала значение среднего, равное 3,0 ф. 95-процентный предел доверитель-

ной вероятности будет

X-1,96 ^<μ<X+1,96^,

или

3,0-0,1 X 1,96 < μ <3,0 + 0,1 χ 1,96;

2,804 <; μ < 3,196.

Теперь мы ожидаем, что случайная выборка, равная 25 замерам, даст

средние, которые окажутся в данном интервале в 95% случаев. Альтерна-

тивная форма этого утверждения о доверительном интервале несколько

шире раскрывает сущность получаемого вывода. Если взяты случайные

выборки по 25 наблюдений каждая и если всякий раз доверительный интер-

вал определяется как указано выше, то в среднем в 95 случаях из 100 этот

интервал накроет истинное среднее μ (фиг. 13.4). Любой отдельный довери-

тельный интервал или будет, или не будет содержать истинное значение μ,

и вышеприведенное утверждение не будет относиться к какому-либо еди-

ничному интервалу; но, если это утверждение сделано по каждому интервалу

в отдельности, требования к нему окажутся несостоятельными в среднем

в пяти случаях из ста.

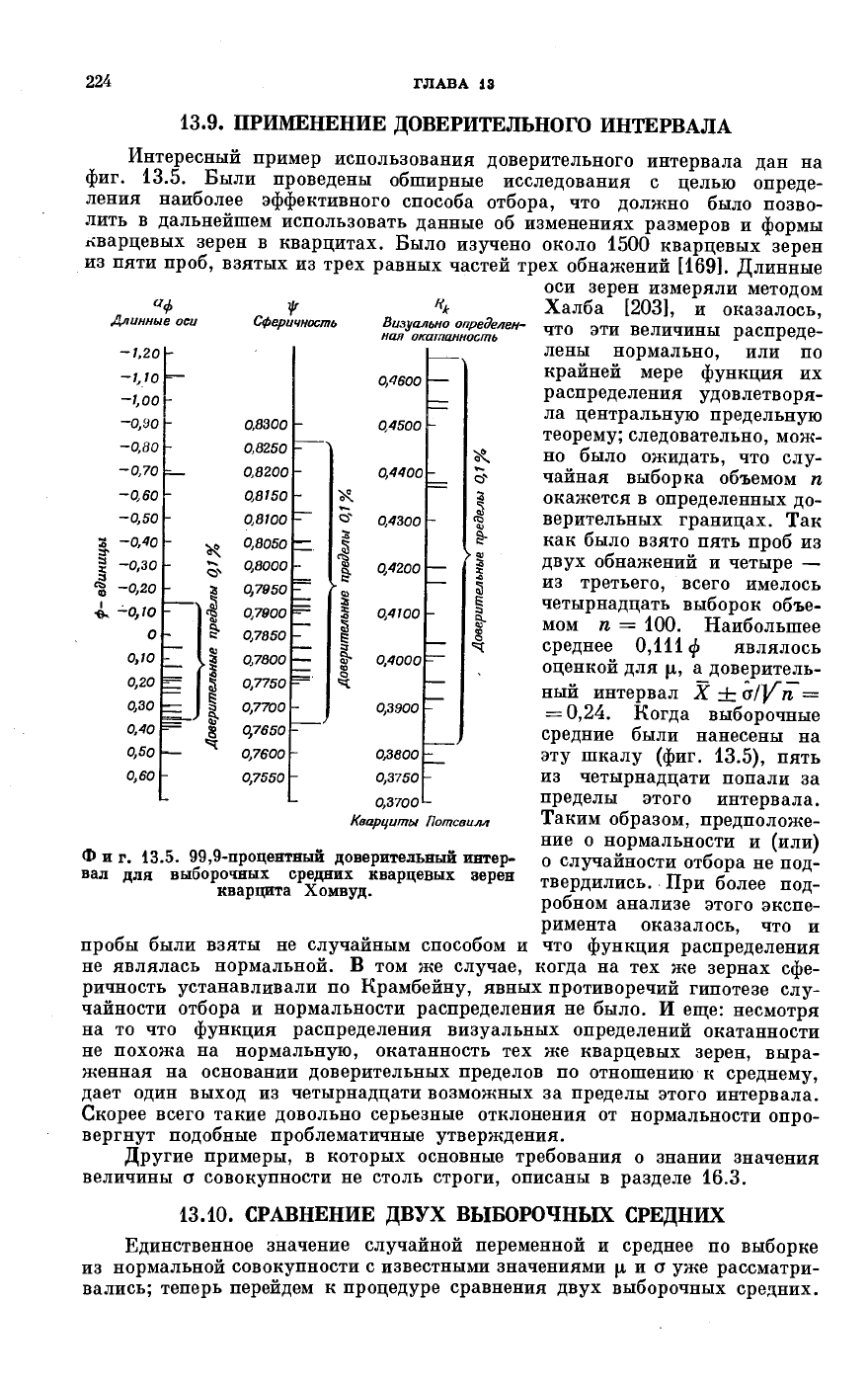
224

ГЛАВА 1 г

Визуально

определен-

ная окатанность

з·

о"

0,1600

0,4500

0,4400

0,4300

0,4200

5 0,4100

S- 0,4000

0,3900

оч

ο-

13.9. ПРИМЕНЕНИЕ ДОВЕРИТЕЛЬНОГО ИНТЕРВАЛА

Интересный пример использования доверительного интервала дан на

фиг. 13.5. Были проведены обширные исследования с целью опреде-

ления наиболее эффективного способа отбора, что должно было позво-

лить в дальнейшем использовать данные об изменениях размеров и формы

кварцевых зерен в кварцитах. Было изучено около 1500 кварцевых зерен

из пяти проб, взятых из трех равных частей трех обнажений [169]. Длинные

оси зерен измеряли методом

Халба [203], и оказалось,

что эти величины распреде-

лены нормально, или по

крайней мере функция их

распределения удовлетворя-

ла центральную предельную

теорему; следовательно, мож-

но было ожидать, что слу-

чайная выборка объемом η

окажется в определенных до-

верительных границах. Так

как было взято пять проб из

двух обнажений и четыре —

из третьего, всего имелось

четырнадцать выборок объе-

мом η = 100. Наибольшее

среднее 0,111 ψ являлось

оценкой для μ, а доверитель-

ный интервал X ± σ/Jin —

= 0,24. Когда выборочные

средние были нанесены на

эту шкалу (фиг. 13.5), пять

из четырнадцати попали за

пределы этого интервала.

Таким образом, предположе-

ние о нормальности и (или)

о случайности отбора не под-

твердились. При более под-

робном анализе этого экспе-

римента оказалось, что и

пробы были взяты не случайным способом и что функция распределения

не являлась нормальной. В том же случае, когда на тех же зернах сфе-

ричность устанавливали по Крамбейну, явных противоречий гипотезе слу-

чайности отбора и нормальности распределения не было. И еще: несмотря

на то что функция распределения визуальных определений окатанности

не похожа на нормальную, окатанность тех же кварцевых зерен, выра-

женная на основании доверительных пределов по отношению к среднему,

дает один выход из четырнадцати возможных за пределы этого интервала.

Скорее всего такие довольно серьезные отклонения от нормальности опро-

вергнут подобные проблематичные утверждения.

Другие примеры, в которых основные требования о знании значения

величины σ совокупности не столь строги, описаны в разделе 16.3.

13.10. СРАВНЕНИЕ ДВУХ ВЫБОРОЧНЫХ СРЕДНИХ

Единственное значение случайной переменной и среднее по выборке

из нормальной совокупности с известными значениями μ и σ уже рассматри-

вались; теперь перейдем к процедуре сравнения двух выборочных средних.

Длинные оси

-1,20

-1,10

-1,00

-Ο,ΰΟ

-0,80

-0,70

-0,60

-0,50

-0,40

-0,30

о -0,20

•L -о, Г О

0,10

0,20

0,30

0,40

0,50

0,60

Сферичность

0,8300

0,3250

0,8200

0,8150

0,8100

0,8050

0,8000

0,7950

0,7900

0,7850

0,7600

0,7750

0,7700

0,7650

0,7600

0,7550

0,3800

0,3750

0,3700

Кварциты Потсвилл

Фиг. 13.5. 99,9-процентный доверительный интер-

вал для выборочных средних кварцевых зерен

кварцита Хомвуд.

ПЛОТНОСТЬ РАСПРЕ ДЕЛЕ HHH

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 225

Примем снова, что функция распределения нормальна и что значения μ

и σ известны. Пока эти требования ограничены некоторыми пределами, они,

во всяком случае приблизительно, выполняются и, вероятно, будут встре-

чаться тем чаще, чем больше новых данных мы будем получать о функции

распределения для применения ее при изучении осадочных пород. Эти тре-

бования можно ослабить (с незначительной потерей эффективности) за счет

использования различных приближений (см. о f-распределении Стьюдента

в разделе 16.4).

Итак, предположим, что, проанализировав две выборки, взятые (опять

по предположению) из нормальной совокупности, мы хотим найти отличия

между двумя полученными средними значениями. Можно рассматривать

реальную ситуацию, при которой длинные оси белых кварцевых галек (выра-

женные в ф-единицах) представляют собой случайную величину X; и два

средних значения получены при опробовании обнажения двумя различными

способами. Функция распределения величины X

приближается к нормаль-

ной, а соответственными статистическими показателями будут: X

= —4,887,

= 0,8516, U

= 336 — по пробам, взятым послойно, и X

= —5,682,

= 0,8070, п

= 300 — по пробам, взятым беспорядочно. Теперь надо

узнать, действительно ли это случайные выборки из некоторой нормальной

совокупности.

Сначала выразим среднее как отклонение от среднего по совокупности,

т. е. разность между средними (X

— μ) — (X

— μ). Можно видеть, что μ

в данном выражении исчезает, остается X

— X

. Если эти средние не раз-

личаются, то X

— X

будет незначимо отличаться от 0; получается, что

мы хотим выразить доверительные границы, которые равно удалены от нуля

и которые показывают, насколько большим может оказаться различие между

случайной величиной из выборки и из нормальной совокупности при μ = 0.

Необходимо получить подходящую оценку для стандартного отклонения σ

из двух оценок, которыми мы располагаем, а затем преобразовать ее в стан-

дартное отклонение.

Дисперсия этой суммы двух случайных величин равна сумме их диспер-

сий и ковариации (смешанный второй центральный момент):

Если случайный отбор каждой пробы проводился независимо, то р = 0,

а выражение принимает вид

Тогда практически мы можем написать, что проверка на различив между

двумя средними из одной и той же нормальной совокупности может быть

выполнена путем подсчета оценочного критерия

4+¾ = 4χ+ 4* ±

, Xi ·

* =

I-

(4^1 + 4^2)

15-429

226

ГЛАВА 1 г

В нашем примере

-4,887-(-5,682) 0,795 0,795 _ ^

~ (0,7253/336 + 0,6510/300)

1/2

~ (0,002159 + 0,001822)

1/а _

0,0631 ~~ '

Если это действительно две случайные выборки из одной и той же нор-

мальной совокупности, такое различие будет в 12,6 раза превышать ее стан-

дартное отклонение, и мы оценим это значение соответственно с данными

фиг. 13.6.

Совершенно очевидно, такое значение встречается редко, что мы можем

заключить, исходя из наших предположений; действительно, площадь огра-

ничения кривой между μ + 12,6σ-^ и μ — 12,6¾ равна 99,99999999, а вне

μ ± 12,6¾ — 0,0000000001. Следовательно, можно ожидать, что значения

будут выпадать из границ ±12,6¾ реже одного раза на каждые IO

испы-

таний. Одно из двух — либо такое редкое событие весьма необычно, либо

О , —^t

Фиг. 13.6. График, поясняющий значение t = 12,6.

мы должны отвергнуть некоторые или даже все наши предположения о слу-

чайности данных выборок из нормальной совокупности. Так как известно,

что эти выборки образуют одну и ту же генеральную совокупность, а нор-

мальность является адекватной аппроксимацией и что даже значительные

отклонения от нее дадут лишь слабый эффект, то опять приходится ставить

вопрос о случайности отбора. Более подробно ознакомиться с этой темой

читатель может по первоисточнику [169].

Прежде чем мы перейдем к рассмотрению критериев значимости, необ-

ходимо сформулировать нулевую гипотезу H

и затем определить те следст-

вия, которые возникнут при проведении описанного эксперимента. Затем

надо произвести эксперимент и совокупность наблюдения сравнить с теми

данными, которые будут продиктованы нулевой гипотезой. Если экспери-

ментальные поиски дадут результат, не сходящийся с гипотезой, мы должны

решить — верить ли этому расхождению или отвергнуть гипотезу. Такое

решение связано с определенным риском, поэтому результат следует сфор-

мулировать в виде вероятностного высказывания. Далее, при эксперимен-

тальной проверке гипотеза может быть отвергнута, но, если этого и не про-

изойдет, обратное утверждение будет заключаться лишь в том, что против

гипотезы нет возражений. Нулевая гипотеза всегда допускает отклонение,

но с некоторыми натяжками. Эксперимент можно считать удачным, если

мы можем произвести строгую проверку нулевой гипотезы и в то же время

отвергнуть разнообразие обстоятельства.

Планирование эффективных экспериментов, которыми можно дейст-

вительно испытать любую нулевую гипотезу, требует известного искусства,

и, кроме того, оно является довольно спорной процедурой (см. гл. 22). Когда

в гипотезе что-нибудь неясно, эта неясность останется и в заключениях,

основанных на проверке гипотезы. Одно из наиболее важных требований при

использовании статистики заключается в возможности выбрать самый под-

ходящий аналитический аппарат для проверки любой гипотезы; широкая же,

общая постановка вопросов приводит к неопределенным, неясным ответам

и оказывает весьма плохую услугу там, где требуется точность и строгость

формулировки.

ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 227

13.11. ЛОГНОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Если наблюдение X включает суммарный эффект большего количества

незначительных причин, действующих случайно, и если каждый эффект

независим от X, распределение, вероятно, будет нормальным. Если оно отли-

чается от нормального, мы вправе предполагать неверно замеренное X.

Находим, что функция f (X) нормально распределена, и поэтому трансфор-

мируем наши наблюдения над X, преобразуя их в наблюдения над

/(X) [138].

Логнормальная плотность распределения была предложена в качестве

модели множества случайных переменных в науках о Земле для случаев

исследований размеров зерен [247, 259, 433], элементов-примесей [5, гл. 4]

и полутораграммовых (24 грана) навесок золотой руды [238, 368, 396, 402];

имеется также много примеров, взятых из других областей [6, 138, 227].

В каждом случае можно привести цитату из критических замечаний по пово-

ду этих предложений. Действительно, невозможно доказать без того, чтобы

не остались сомнения, что распределение некоторой случайной величины

задано в форме некоторой точно определенной функции. Например, когда

оспаривались предложения Стьюдента по модели Пуассона [451], он после-

довательно объяснил, что до тех пор, пока практически невозможно точно

отобразить кривую по точкам, модель Пуассона хотя и остается приближен-

ной, тем не менее она представляет определенную ценность. Единственно,

чем можно логически оправдать принятие какой-либо функции распределения

в качестве модели,— это более быстрым достижением цели с помощью рас-

сматриваемой функции. И в этом смысле следует рекомендовать логнормаль-

ное распределение для изучения изменений размеров осадочных частиц.

Так как это одно из наиболее ценных и обычных применений, нелишне изу-

чить некоторые детали той процедуры, которая называется применением

функции распределения.

Обоснование применимости модели функции распределения может сле-

довать тремя путями. Во-первых, можно теоретически постулировать физи-

ческие условия, характеризующие естественный процесс, который приводит

именно к данному распределению случайной величины; затем можно пока-

зать, что это распределение удовлетворяет требованиям, которые следуют

из некоторой определенной функции. (Пример использования модели Пуас-

сона для повышения качества изготовления микроскопических препаратов

для исследования акцессорных минералов описан в разделе 14.7.) Во-вторых

(альтернативный путь), с помощью той же модели можно изучить плотность

распределения данной случайной величины в относительно большой выборке

с последующим показом [при помощи подходящей процедуры, какой, напри-

мер, является анализ моментов, и (или) с помощью критерия согласия χ

как эмпирически установленная функция распределения хорошо согла-

суется с некоторой уже известной функцией. Трудность достижения такого

эмпирического согласования заключается в том, что исследуемая выборка

должна быть действительно случайной. Если же отбор данных не случаен,

функция распределения может не согласоваться с ожидаемым результатом.

В-третьих, с целью окончательного дедуктивного согласования можно

использовать оба указанных пути: подходящая теоретическая модель разра-

батывается на основе уже известных данных об изменениях случайной вели-

чины; затем прогнозируется выборочное распределение статистических харак-

теристик, которое проверяется путем случайного отбора. Конечно, почти

всегда есть возможность так подобрать выборочное расположение, чтобы

распределение случайной величины удовлетворяло любым определенным

требованиям. Поэтому окончательное согласование в значительной мере

зависит от того, действительно ли принятая модель и все данные, связанные

с ней, соответствуют наблюдениям. Весь ход рассуждений о нормальной

15*

228

ГЛАВА, 13

модели, вызванных классической критикой Пуанкаре ([332], цитирован

по работе [138]; на эту работу ссылается любой, кто сомневается в существо-

вании нормального распределения, которое стало к настоящему времени

общепризнанным; см., например, [18, 98, 99, 215]),свидетельствует о том.

что получить это доказательство действительно трудно, а может быть,

и невозможно. Мы же, как последователи Стьюдента, будем придерживаться

следующего взгляда: то, к чему мы стремимся, заключается в приближении,

которое позволит достичь нашей цели. Но если перед нами встанет лучшая

альтернатива, она также должна быть рассмотрена, насколько это возможно

и без каких-либо предубеждений.

13.12. НЕКОТОРЫЕ]ТЕОРЕТИЧЕСКИЕ СООБРАЖЕНИЯ О ПРИМЕНЕНИИ

ЛОГНОРМАЛЬНОЙ МОДЕЛИ ДЛЯ ИЗУЧЕНИЯ ФУНКЦИИ

РАСПРЕДЕЛЕНИЯ РАЗМЕРОВ ЧАСТИЦ

Измеряя размеры зерен осадочных пород, мы обычно преследуем неко-

торый конечный результат, который в общем является попыткой определить

условия образования осадка по данным о функции распределения этих

размеров. Например, предполагается, что размеры зерен отражают скорость

течения, и, чтобы установить зависимость между размерами зерен и скоростью

течения, надо провести многочисленные и обширные исследования (см.,

например, работы [141, 308]). Описание зависимости между скоростью тече-

ния и размерами частиц обычно основано на идеальных «законах», какими

являются, например, закон Стокса и закон столкновений; первый описывает

это соотношение для частиц в ламинарном потоке, второй — для грубых

частиц и в турбулентном потоке [308]. Оба «закона» могут выражаться линей-

ными зависимостями после логарифмического преобразования, как это

показано в табл. 13.6.

Таблица 13.6

Связь между скоростью течения и размером частиц,

выраженным через радиусы

—

скорость, см/сек; С

—

константа; г

—

радиус, см

Закон

Зависимость

Логарифмическое выражение

зависимости

Стокса

Столкновений

F = C>2

Vi = Cr

log V

=Iog С + 2 log г

2 log V = Iog С+log г

В тех областях, где эти законы действуют, существует прямое взаимно

однозначное соответствие между логарифмом скорости и логарифмом радиуса

частицы; если радиусы частиц распределены логнормально, так же распре-

делены и их скорости, и наоборот.

Обоснование предположения, согласно которому логнормальная модель

зависит от того, насколько реально существование логнормального закона,

заключается в описании изменений скорости потока, которые ожидаются

в обычных условиях перемещения жидкости. Так как оба закона действуют

в ограниченных областях поля возможных взаимоотношений пары «части-

ца скорость» и так как между этими законами существует переходная

область (где частицы сальтируют), данная модель только приблизительно

отражает положение дел. Ее ограничения прежде всего зависят от размеров

этой переходной области — достаточно ли она узка, чтобы ею можно было

пренебречь, при достижении большинства практических целей, т. е. резок

ли переход от ламинарного течения к турбулентному в природных условиях

ПЛОТНОСТЬ РАСПРЕ ДЕЛЕ HHH

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 229

[308]. Если это приемлемо, можно изучать дальнейшие следствия логнормаль-

ной модели по данным скоростей и переходить от логарифма скорости обратно

к ее значению по первоначальной шкале, наблюдая при этом, что именно

«предвещает» результирующая кривая. Пример пользы такой процедуры

при изучении размеров зерен приводят Гриффите и др. [164]. Результирую-

щая кривая для этого случая изображена на фиг. 13.7.

На ней показано, что не существует скорости, равной нулю или менее;

разумеется, в естественных условиях иногда прекращается движение потока

на какой-то период, но это нельзя рассматривать в качестве обычного состоя-

ния движения жидкости. Весьма большие скорости также в природе редки

(чем выше скорость, тем реже она встречается).

Когда преобладает скорость меньше средней, кривая сильно скаши-

вается в сторону больших скоростей, что совершенно определенно отражает

Фиг. 13.7. Гипотетическая плотность распреде- а-

ления скорости в потоке жидкости при естествен-

ных условиях.

условия почти всех потоков воды, льда, воздуха, даже условия гравита-

ционного скольжения, и что весьма близко к тем условиям, которые дей-

ствительно наблюдаются в природе. Для проверки конкретных форм кривой

могут быть использованы реальные наблюдения [247, 387].

Таким образом, следует считать, что логнормальная модель распреде-

ления скоростей и отсюда логнормальная модель распределения размеров

частиц являются достаточно приемлемыми аппроксимациями, исходящими

из гипотетических физических условий. Если теперь мы попытаемся иссле-

довать согласованность некоторых видов эмпирического распределения

частиц с этими теоретическими предположениями, следует быть осторож-

ными в требованиях к модели. Эти требования необходимо предварительно

изучить; к счастью, они исключительно хорошо зафиксированы и ими поль-

зовались во многих ситуациях, аналогичных той, с которой мы имеем дело

при изучении размеров частиц (см., например, работы [6, 138, 227]).

Одно из существенных требований заключается в том, что на у'-й стадии

изменение случайной величины должно выражаться случайной долей от

функции φ (Xj-г), т. е. того значения, которое уже достигнуто; следова-

тельно, следуя Кэптейну [227], Эйтчисону и Брауну \

Xj-XJ., = г

}

ф (XJ^

), (13.8)

где множества {ε^} взаимно независимы и независимы также от множест-

ва {Xj}. Поэтому изменения на каждой стадии не независимы от достигну-

тых значений, за исключением тех случаев, когда φ (X) = 1 и φ (X) = 0.

Мы можем выделить характерный случай, когда φ (X) = X; изменение

этой случайной переменной является случайным соотношением мгновенного

(единичного) значения случайной переменной. Закон пропорционального

эффекта описывает это взаимоотношение таким образом.

Говорят, что случайная величина, подвергаемая процессу изменений,

описывается законом пропорционального эффекта, если ее изменение на

любой стадии процесса находится в случайном соотношении с первона-

чальным значением этой переменной; исходя из сказанного, можно напи-

Нижеприведенные данные взяты из работы [6, стр. 22—23].

230

ГЛАВА 13

сать, что

или

-X

-U (13.9)

— Xj-1

. J =Sj- (13.10)

Суммировав по всем η значениям данной случайной переменной,

получаем

2¾

=!!^ (I3.LI)

з=1 ' з=1

предположив, что изменения на каждом шаге достаточно малы,

Хп

^ { ^ = [log = log Z

- log X

. ' (13.12)

3=1

Возвращаясь к равенству (13.10), имеем

log X

= log X

+ . .. + ε„. (13.13)

С учетом дополнительной формы центральной предельной теоремы

величина log X

распределена приблизительно нормально.

Можно, конечно, обобщив условия, использовать' распределения

с двумя и более параметрами, но можно также приспособить эту модель

для изучения скорости и (что аналогично) плотности распределения разме-

ров частиц. Следовало бы подчеркнуть, что, если мы хотим сделать эту модель

достаточно приемлемой, переменная, используемая для измерения размеров

частиц, должна отражать только детритные составляющие Кроме того,

почти наверняка придется предположить, что ни состав, ни строение агре-

гата не оказывают влияния на данные измерений. Иными словами, данная

модель применима только к однокомпонентным системам со случайным

распределением отклонений. Это помогает улучшить косвенные способы

измерений размеров частиц и, возможно, методику изучения шлифов, если

материал, подлежащий исследованию, нельзя считать приблизительно моно-

минеральным и если размеры составляющих однородны. Фактически мы при-

ходим к необходимости фиксировать размеры частиц [и (или) их форму]

прямыми способами.

Если мы теперь продолжим изучение способов определять распределе-

ние размеров частиц, то найдем, что некоторые распределения являются

действительно логнормальными, но что есть много и таких, которые не под-

чиняются этому правилу. Большое количество последних может появиться

из-за неправильного выбора меры частиц вследствие многокомпонентности

их материала, как это и бывает в большинстве случаев при изучении осадоч-

ных пород. Примеры тому наблюдаются при косвенных измерениях раз-

меров зерен граувакк и аркозов [39, 99]. Но и при почти мономинеральном

составе осадков неудача в деле построения нормальной модели может объяс-

няться неслучайностью замеров [215] даже в том случае, когда фактор состава

не имеет большого значения, как в этом можно убедиться при изучении мно-

гих пляжных и дюнных песков

Если не приняты соответствующие предосторожности для обеспечения

случайности выборки, плотность распределения снова существенно откло-

нится от нормальности [18, 318]. В тех же случаях, когда надлежащий выбо-

рочный план определен, а осадок или агрегат монодисперсен, в очень многих

видах материала размеры частиц распределены логнормально [188, 189].

Практически закон переноса может быть выражен также в логнормальной форме

[116].

Также искусственных смесей [12, 215, 216].

ПЛОТНОСТЬ РАСПРЕ ДЕЛЕ HHH

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 231

Можно очень просто показать, что даже при всех мерах предосторож-

ности, направленных на сохранение постоянства состава, если выборка

не случайна, плотность распределения будет отличаться от логнормальной,

в то время как та же совокупность опробования случайным способом при

той же процедуре измерения не даст сколько-нибудь заметных отклонений

от логнормальности даже при строгом подходе [169, 170].

Некоторые примеры плотности распределения размеров зерен, на кото-

рых выполняются требования к рассматриваемой модели, уже описаны

(раздел 5.5 и последующие), и пригодность логнормальной модели была

доказана. Если мы примем эту модель в качестве подходящей аппроксимации,

то можем затем использовать данные о свойствах нормального распреде-

ления для предсказания определенных исходов эмпирического анализа

и эффективно использовать такие процедуры контроля, как проверка слу-

чайности выборки. В действительности, как отмечено выше (стр. 197), мы

можем определить заданную модель функции распределения как соот-

ветствующую некоторому теоретическому, случайному процессу опробо-

вания и определить по смещению, обнаруженному в результате эмпирических

измерений, характер изменчивости в данной совокупности, т. е. определить

структуру материала путем опробования.

В случайных выборках, имеющих нормальную функцию распределе-

ния, среднее не зависит от дисперсии, и можно постулировать на основании

этой гипотезы, что не должно быть взаимосвязи между средним и дисперсией,

в частности между статистическими критериями оценки этих параметров.

Чтобы мы могли охарактеризовать процессы седиментации, исходя из сме-

щений, характерных для среднего и дисперсии (например, размер частиц

и их сортировка; см. гл. 15), необходимо изучить взаимоотношения между

ними. Ценно то, что в трех областях этих взаимоотношений (см. фиг. 15.1)

даже косвенные методы измерений дают нормальное распределение;

и в каждом таком случае осадок оказывается близким к однокомпонентной

системе: это глины, кварциты (сюда следует включить пляжные и дюнные

пески) и некоторые гравеллиты с преобладанием какого-либо одного эле-

мента (частицы). Опять же, когда подвергаются обработке таким же спосо-

бом измерения в шлифах, найденное среднее почти всегда будет независимым

от дисперсии ([164, 167] и раздел 5.7); это приводит к выводу, что в подобных

условиях измерения мы скорее всего имеем дело со случайной выборкой

из нормально распределенной совокупности.

Окончательно можно сказать, что, когда применяются прямые изме-

рения, может быть использована взаимосвязь между средним и дисперсией

для освещения структурного упорядочивания данной совокупности по раз-

мерам зерен посредством карт количественного контроля (фиг. 2.5).

Полагаем, что применение логнормальной функции в качестве модели

распределения при изучении размеров зерен, если соблюдены соответствую-

щие предосторожности [176], оказывает существенную помощь в деле объек-

тивного понимания процессов седиментации. Главные условия, необходимые

для получения логнормальной модели, следующие:

1. Выбранная для зерен мера должна интерпретироваться физически просто, напри-

мер представлять собой определенный отрезок единого однородного минерального соста-

вляющего. Для выполнения этого требования выбранную меру надо интерпретировать

непосредственно по той величине или понятию, которые она отражает, например по той

мере, которая эквивалентна размерам и величине, а эти последние в свою очередь должны

быть эквивалентными скорости перемещения частиц.

2. Следует достигнуть случайного опробования, т. е. простой метод случайного

опробования требует постоянства вероятности от испытания к испытанию. При страти-

фицированных совокупностях это означает следующее: или нужны бороздовые пробы,

которые удовлетворяли бы требованиям простого случайного опробования путем опро-

бования всей генеральной совокупности в любом случае, или стратифицированное слу-

чайное опробование, когда случайные выборки берутся из однородных осадочных под-

разделений.