Гриффитс Дж. Научные методы исследования осадочных пород

Подождите немного. Документ загружается.

212

ГЛАВА 1 г

другая статистическая оценка не в состоянии дополнительно осветить пара-

метр сдвига. Наилучшая оценка σ

в равной мере достаточна в том отношении,

что никакая другая оценка ничего не добавит к информации о дисперсии рас-

пределения. К сожалению, оценок, обладающих свойством достаточности,

немного; однако среднее арифметическое полностью отвечает требованиям

достаточности при нормальном или при пуассоновом распределении. Боль-

шинство других оценок, таких, как медиана или квартиль, по сравнению

с подходящими оценками при нормальном распределении не эффективно

{96, 291]. Разумеется, никакие сравнения делать нельзя, пока функция плот-

ности вероятности точно не определится, так что во многих случаях невоз-

можно решить, какую из предлагаемых статистик можно считать подходя-

щей для оценивания. В общем рекомендуем отбирать те статистики, которые

удовлетворяют вышеприведенным требованиям «самой лучшей» или по край-

ней мере тем требованиям, которые могут быть предъявлены в каком-то

данном случае. Возможно, что именно в этом крайнем случае особо потре-

буются свойства состоятельности и несмещенности.

Общие рекомендации, следующие из сказанного, заключаются в том,

что знать вид функции распределения необходимо во всех случаях и что

без такой информации делать какие-либо правдоподобные заключения

невозможно. Большинство методов, рекомендуемых в этой книге, при соот-

ветственном их использовании дает возможность получить достаточные све-

дения о функции распределения, применить весь набор описанных оценок

и уверенно использовать статистический анализ даже в самом сложном виде.

Чем меньше известно о функции распределения случайной величины, тем

труднее достигнуть надежных выводов и решений геологических проблем:

в этом смысле «непараметрические», или «порядковые», статистики следует

рассматривать лишь как временные заменители более надежного анализа,

и к заключениям, основанным на подобных критериях, следует относиться

весьма осторожно.

ГЛАВА 13

Плотность распределения.

Нормальное распределение

Говорят., что случайная величина распределена нормально, если она

принимает любые значения в интервале от —оо до + оо с частотами,

которые подчиняются определенному математическому закону, а именно:

логарифм частоты, соответствующей любому расстоянию от центра

распределения, меньше логарифма частоты, соответствующей центру,

на величину, пропорциональную величине d

R. A. Fisher, Statistical Methods for Research Workers, IOht

ed., Oliver and Boyd, Ltd., p. 43, 1948

13.1. ВВЕДЕНИЕ

Функция распределения играет главную роль при статистической обра-

ботке данных, полезность которых может рассматриваться с различных точек

зрения. Обычно распределение изображается в виде наглядных графиков.

При этом статистические результаты, видимо, легче понять, если восприни-

мать их как «облик» распределения.

Если известно, что некоторый экспериментальный процесс характери-

зуется определенным типом распределения, то сравнение наблюдаемых

данных с данными экспериментального опробования составляет проверку

случайности отбора наблюдений.

Помимо аспектов, относящихся к физической интерпретации распре-

деления, последние можно специально использовать и для формулировки

основных правил статистического анализа; знание вида распределения позво-

ляет предсказать выборочное распределение определенной оценки, например

выборочного среднего и дисперсии при нормальном распределении. Это в свою

очередь приводит к задачам проверки гипотез и проблемам оценки неизвест-

ных параметров по статистической выборке.

Совокупность наблюдений нельзя использовать для определенных спе-

цифических видов анализа без перехода к новой шкале, и в таких случаях

для выбора надлежащего способа трансформации данных необходимо знать

вид распределения (гл. 15).

Цель последующего изложения — кратко описать некоторые из обыч-

ных видов распределений, которые фиксируются экспериментально; без

знания свойств этих распределений нельзя описать выборочные ситуации,

возникающие как при физических опытах, так и при статистическом анализе.

Следует помнить, что одно и то же распределение можно использовать при

решении разных задач, поэтому всегда необходимо установить цель анализа,

если мы хотим достичь ясности и понимания.

214

ГЛАВА 1 г

13.2. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Нормальное, или гауссово, распределение случайных величин (рас-

пределение ошибок) наиболее распространено и широко применяется среди

различных видов распределений.

Это одна из наиболее ранних статистических закономерностей, впервые

использованная Муавром примерно в 1758 г. [441], играет значительную

роль в теории ошибок [26]. Нормальное распределение часто используется

как физическая модель, оно является главным видом распределения в пара-

метрическом статистическом анализе. Его обычно используют также в каче-

стве эталона при сравнении непарамет-

рических критериев для характеристи-

ки мощности и эффективности.

Рассмотрим семейство кривых

72=^

2/2

» (13-1)

-4 -3 -2

к =1

1 ^X

к>1

1 2 3

Фиг. 13.1. Графическое изображение

функции у — k~

12/

где к — постоянная, а у и t — пере-

менные. Примем к = 1, тогда кривая

будет представлять собой прямую, па-

раллельную оси t (фиг. 13.1). При к <; 1

кривая U-образна с перегибом, находя-

щимся выше уровня у = 1. При к > 1

она принимает колоколообразную фор-

му, как это показано на фиг. 13.1.

Обычно постоянная к выбирается такой, чтобы получилась кривая,

ограничивающая площадь, равную единице; этому условию удовлетворяет

к — 1,0872. Форма постоянной к определяется как (\lV2n) е, где е — осно-

вание натуральных логарифмов, а π — постоянная.

Формула для кривой распределения, таким образом, приобретает вид

У 2л

-ty 2.

(13.2)

она называется стандартной нормальной кривой. Этой формулой принято

выражать нормальную плотность распределения, но прежде надо произвести

замещение, т. е.

ί=^, (13.3)

откуда

σ V 2л

ехр

(13.4)

Параметрами нормальных распределений, по которым их можно различать,

является среднее μ и стандартное отклонение а. Если задана некоторая

частная нормальная кривая, то μ и α фиксированы, а изменения у в зави-

симости от X можно изучать. Площадь, ограниченная кривой распределе-

ния, равна единице. Таким образом, каждое приращение площади представля-

ет некоторое отношение. Очень важны площади, ограниченные разными орди-

натами. К сожалению, правая часть приведенного выражения не может быть

проинтегрирована в данной его форме, и площади, лежащие между задан-

ными ординатами, находят с помощью приближенных методов.

Значения площадей между заданными ординатами нормального рас-

пределения табулированы и для удобства приведены в соответствие со стан-

дартной нормальной кривой.

ПЛОТНОСТЬ РАСПРЕ ДЕЛЕ HHH

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 214

Для примера предположим, что получена некоторая кривая нормаль-

ного распределения с μ = 10 и а = 5. Тогда подстановкой t — (X — μ)/σ =

— (X — 10)/5 функция распределения

[-WTl <«·

приводится K ВИДУ

'=^-T-. (

где μ = 0 и σ = 1. Подобная подстановка применяется для всех нормальных

кривых, использующих приближенные значения μ и σ; независимой пере-

менной таблиц соответствуют χΐσ, где χ = X — μ. Таким образом, одна таб-

лица дает информацию о площадях для всех нормальных кривых (см., на-

пример, [15, табл. 10; 323, табл. 1]).

13.3. ХАРАКТЕРИСТИКИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ

Кривая плотности вероятности нормального распределения симметрична

по отношению к среднему (фиг. 13.1); площадь, ограниченная этой кривой

и ординатой в точке X, равна частоте, т. е.

В случае стандартного нормального распределения площадь, огра-

ниченная кривой, равна единице.

Формы, или виды, частотных кривых описываются по-разному; одним

из наиболее распространенных способов представления этих кривых явля-

ется метод моментов и переход к бета-статистикам Пирсона [111], которые

можно применять к разнообразным частотным кривым.

В случае нормального распределения основными параметрами, бази-

рующимися на моментах, являются следующие:

Таблица 13.1

Параметр

Соответствующий

момент, порядок

Площадь

Нулевой

Среднее

Первый

Стандартное отклонение

Второй

Асимметрия

Υβι=ο

Третий

Эксцесс

= 3 Четвертый

•

Существует множество различных мер асимметрии и эксцесса,

например, такие, как g-статистика Фишера, базирующаяся на семи-

инварианте , которая весьма полезна [127].

Площадь, ограниченная кривой нормального распределения, есть момент

нулевого порядка.

13.4. УСЛОВИЯ, ПРИВОДЯЩИЕ К НОРМАЛЬНОМУ РАСПРЕДЕЛЕНИЮ

Использование кривой плотности распределения в качестве физической

модели некоторой экспериментальной выборки требует знания тех условий,

которые приводят к нормальному распределению.

Проще всего, видимо, начать с требований для симметричного бино-

миального распределения

Эти условия детально изучены Смитом и Дунканом [407].

216

ГЛАВА 1 г

1. Еслк отсутствуют определенные «причины» изменчивости или же

в случае полного взаимного уравновешивания этих причин, в выборке может

быть зафиксировано некоторое центральное значение.

2. Отклонения фактических значений случайных величин от этого

центрального значения происходят в результате определенных причин;

эффект действия какой-либо причины заключается или в определенном уве-

личении, или в таком же уменьшении значения случайной величины (по

сравнению с уже фиксированным центральным значением).

3. Вероятность того, что причина изменчивости даст положительный

эффект, равна вероятности появления отрицательного эффекта:

P( + ve) = P(-Oe) = \.

4. Причины, содействующие изменениям в одном направлении, в равной

мере и с равной интенсивностью действуют во всех направлениях.

5. Причины изменений независимы в своем действии; вероятность

P (-\-ve) или P (—ve) для любого причинного фактора независима от перво-

начальных условий.

6. Суммарное отклонение любого замера от центрального значения

получается как алгебраическая сумма влияния всех положительно и отри-

цательно действующих отдельных факторов.

Кроме того, следует прибавить, что кривая нормального распределения

будет получена, когда:

7. Количество действующих причин очень велико.

8. Положительный или отрицательный эффект действия каждой причины

очень мал.

Фактически многие из перечисленных требований можно ослабить, так

как нормальное распределение возникает при весьма общих условиях.

Наиболее важны условия требований 6, 7, 8 и, видимо, 4. Если будут соблю-

дены условия б, 7, 8, то условия 2 и 3 могут оказаться менее существенными.

Если изучаемая случайная величина удовлетворяет этим требованиям, плот-

ность ее распределения можно рассматривать как нормальную и в качестве

основы для анализа выборок, получаемых при экспериментальном исследо-

вании, использовать нормальную модель.

13.5. СВЯЗЬ ВЫБОРОЧНЫХ РАСПРЕДЕЛЕНИЙ С НОРМАЛЬНЫМИ

Одно из первых требований для применения нормальной модели —

необходимость испытать, можно ли данный набор наблюдений, представляю-

щий выборку, считать взятым из совокупности, обладающей нормальным

распределением. Процедура проверки начинается с определения выборочных

статистик среднего X, стандартного отклонения σ, асимметрии Ύ Ъ или

эксцесса Ь

или g

Если наблюдения составляют случайные выборки из нормально рас-

пределенной совокупности, то среднее X является оценкой для неизвестного

среднего μ всей совокупности, а выборочное стандартное отклонение σ можно

использовать как оценку для σ. Процедура приведения выборочного рас-

пределения кривой к стандартной форме заключается в вычитании среднего

из значения каждого наблюдения и в. нормировании отклонения X — μ

делением его на оценку стандартного отклонения σ. При этом обычно исполь-

зуется нормальное распределение отклонений со средним, равным нулю,

и дисперсией, равной единице, и результат выражается переменной Z [96].

На практике наблюдения разносят по интервалам группировки, затем

находят площади между границами интервалов, для чего границы центри-

ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 217

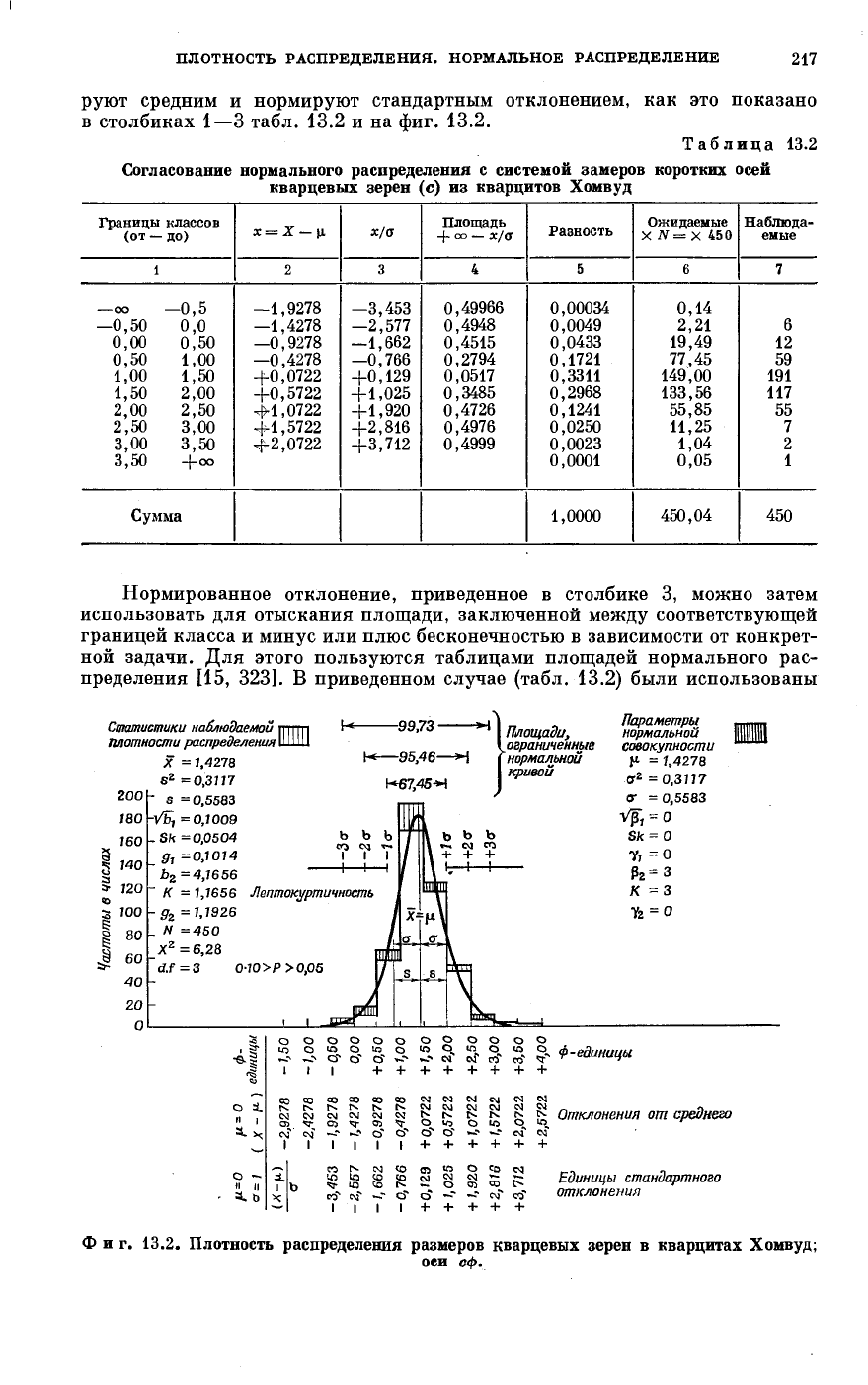
руют средним и нормируют стандартным отклонением, как это показано

в столбиках 1—3 табл. 13.2 и на фиг. 13.2.

Таблица 13.2

Согласование нормального распределения с системой замеров коротких осей

кварцевых зерен (с) из кварцитов Хомвуд

Границы классов

х/о

Площадь Ожидаемые Наблюда-

(от

—

до)

χ = X

—

х/о

со —

х/а

X N = χ 450 емые

1 2

3 4

5 6

—0,5

-1,9278

—3,453

0,49966

0,00034

0,14

—0,50

0,0

—1,4278 —2,577

0,4948 0,0049 2,21 6

0,00

0,50

—0,9278 -1,662 0,4515 0,0433

19,49

0,50

1,00

—0,4278 —0,766

0,2794 0,1721

77,45

1,00 1,50 +0,0722

+0,129 0,0517

0,3311

149,00 191

1,50 2,00 +0,5722 +1,025 0,3485

0,2968 133,56 117

2,00

2,50

+1,0722

+1,920

0,4726

0,1241 55,85 55

2,50

3,00

+1,5722 +2,816 0,4976 0,0250

11,25

3,00

3,50

+2,0722 +3,712 0,4999 0,0023

1,04

3,50

+ OO

+3,712

0,0001

0,05 1

Сумма

1,0000

450,04

450

Нормированное отклонение, приведенное в столбике 3, можно затем

использовать для отыскания площади, заключенной между соответствующей

границей класса и минус или плюс бесконечностью в зависимости от конкрет-

ной задачи. Для этого пользуются таблицами площадей нормального рас-

пределения [15, 323]. В приведенном случае (табл. 13.2) были использованы

Статистики наблюдаемой птттп

Плотности распределения IHlIlI

X = 1,4278

=0,3117

" s =0,5583

-Yb

=0,1009

- Sk =0,0504

9, =0,1074

=4,7656

К = 1,76 5 6

Мептокуртичность

- д

= 7,7926

, N = 450

=6,28

d.f =3 0-10>Р>0,05

-99,73

•

200

/80

160

140

э·

120

«а

•о

100

Sr-

—95,46—H

К67.45-Ч

Площади,

jограниченные

"нормальной

кривой

Параметры

нормальной

совокупности

Jt =7,4278

= 0,3737

or =0,5583

= O

Sic = О

γ, =о

K= 3

= O

о а.

π ι

а- ч

—

<1 Il

а. ъ

OOOOO OO OO OO

0 ю о в о « ч «2 О, ю о ф-единиим

CT О О W -.- Cf N со то" τ

кииницы

1 I + + + + ++ + +

comcocococoCMWNcsiWN

Г. Г", N N (Μ CvJ CNJ <N JN

NNWNWCiNN' ' ^fv

о οϊ Oj O io

СчГ cvj" о о" о"' О Ο-

Ι I I I I

о ю

+ + + +

g £ Отклонения от среднего

CM CM

+ +

TOr^lNCOroWOCDcq

» В Ч> N - OOlCOf-

of с? с> —' —' Ν" со"

I I I I + + + + +

Единицы стандартного

отклонения

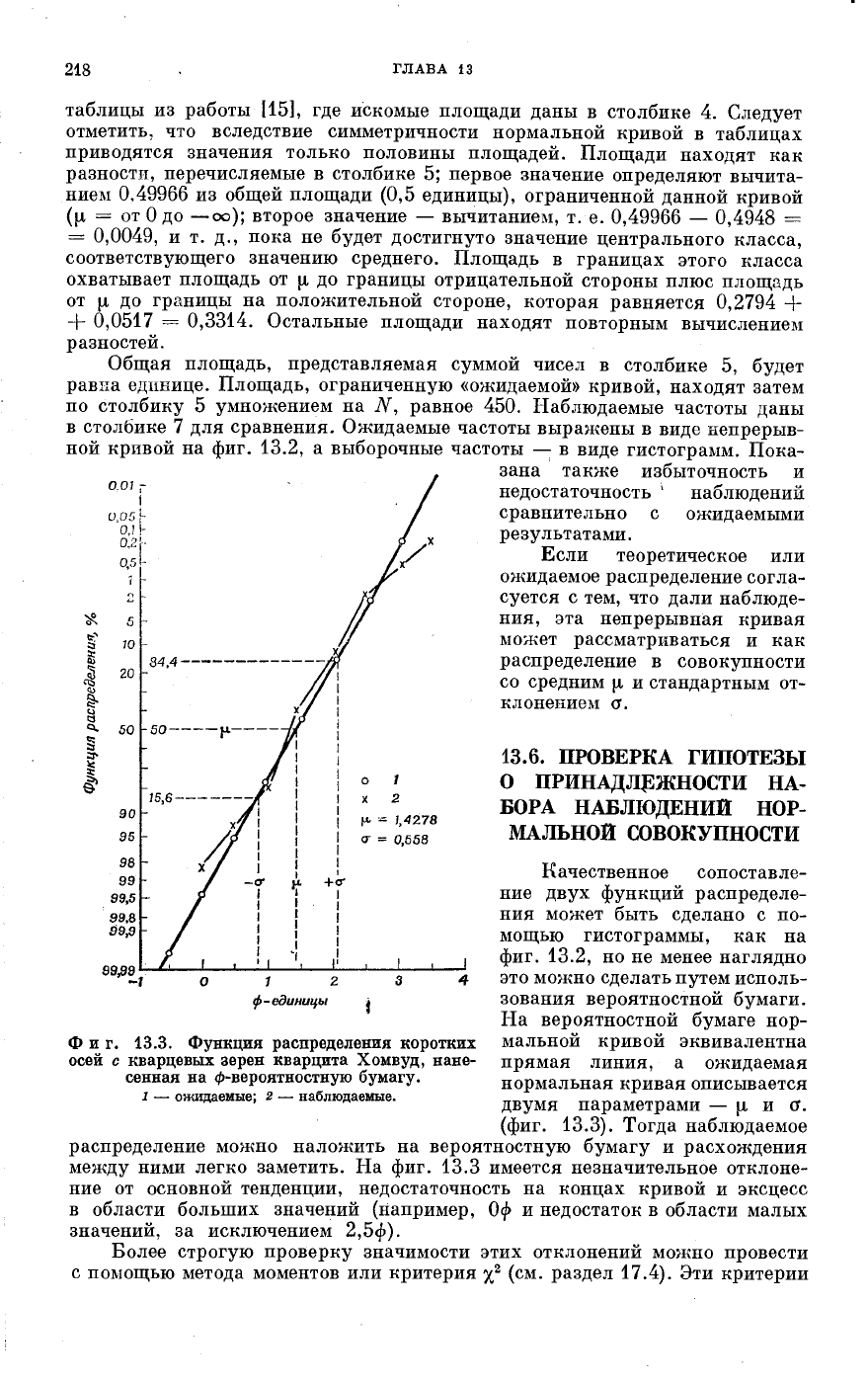
Фиг. 13.2. Плотность распределения размеров кварцевых зерен в кварцитах Хомвуд;

оси сф.

218

ГЛАВА 1 г

таблицы из работы [15], где искомые площади даны в столбике 4. Следует

отметить, что вследствие симметричности нормальной кривой в таблицах

приводятся значения только половины площадей. Площади находят как

разности, перечисляемые в столбике 5; первое значение определяют вычита-

нием 0.49966 из общей площади (0,5 единицы), ограниченной данной кривой

(μ = от 0 до —сю); второе значение — вычитанием, т. е. 0,49966 — 0,4948 =

= 0,0049, и т. д., пока не будет достигнуто значение центрального класса,

соответствующего значению среднего. Площадь в границах этого класса

охватывает площадь от μ до границы отрицательной стороны плюс площадь

от μ до границы на положительной стороне, которая равняется 0,2794 +

+ 0,0517 = 0,3314. Остальные площади находят повторным вычислением

разностей.

Общая площадь, представляемая суммой чисел в столбике 5, будет

равна единице. Площадь, ограниченную «ожидаемой» кривой, находят затем

по столбику 5 умножением на Ν, равное 450. Наблюдаемые частоты даны

в столбике 7 для сравнения. Ожидаемые частоты выражены в виде непрерыв-

ной кривой на фиг. 13.2, а выборочные частоты — в виде гистограмм. Пока-

зана также избыточность и

недостаточность

сравнительно с

результатами.

Если теоретическое или

ожидаемое распределение согла-

суется с тем, что дали наблюде-

ния, эта непрерывная кривая

может рассматриваться и как

распределение в совокупности

со средним μ и стандартным от-

клонением σ.

наолюдении

ожидаемыми

ф-единицы

13.6. ПРОВЕРКА ГИПОТЕЗЫ

О ПРИНАДЛЕЖНОСТИ НА-

БОРА НАБЛЮДЕНИЙ НОР-

МАЛЬНОЙ СОВОКУПНОСТИ

Качественное сопоставле-

ние двух функций распределе-

ния может быть сделано с по-

мощью гистограммы, как на

фиг. 13.2, но не менее наглядно

это можно сделать путем исполь-

зования вероятностной бумаги.

На вероятностной бумаге нор-

мальной кривой эквивалентна

прямая линия, а ожидаемая

нормальная кривая описывается

двумя параметрами — μ и в.

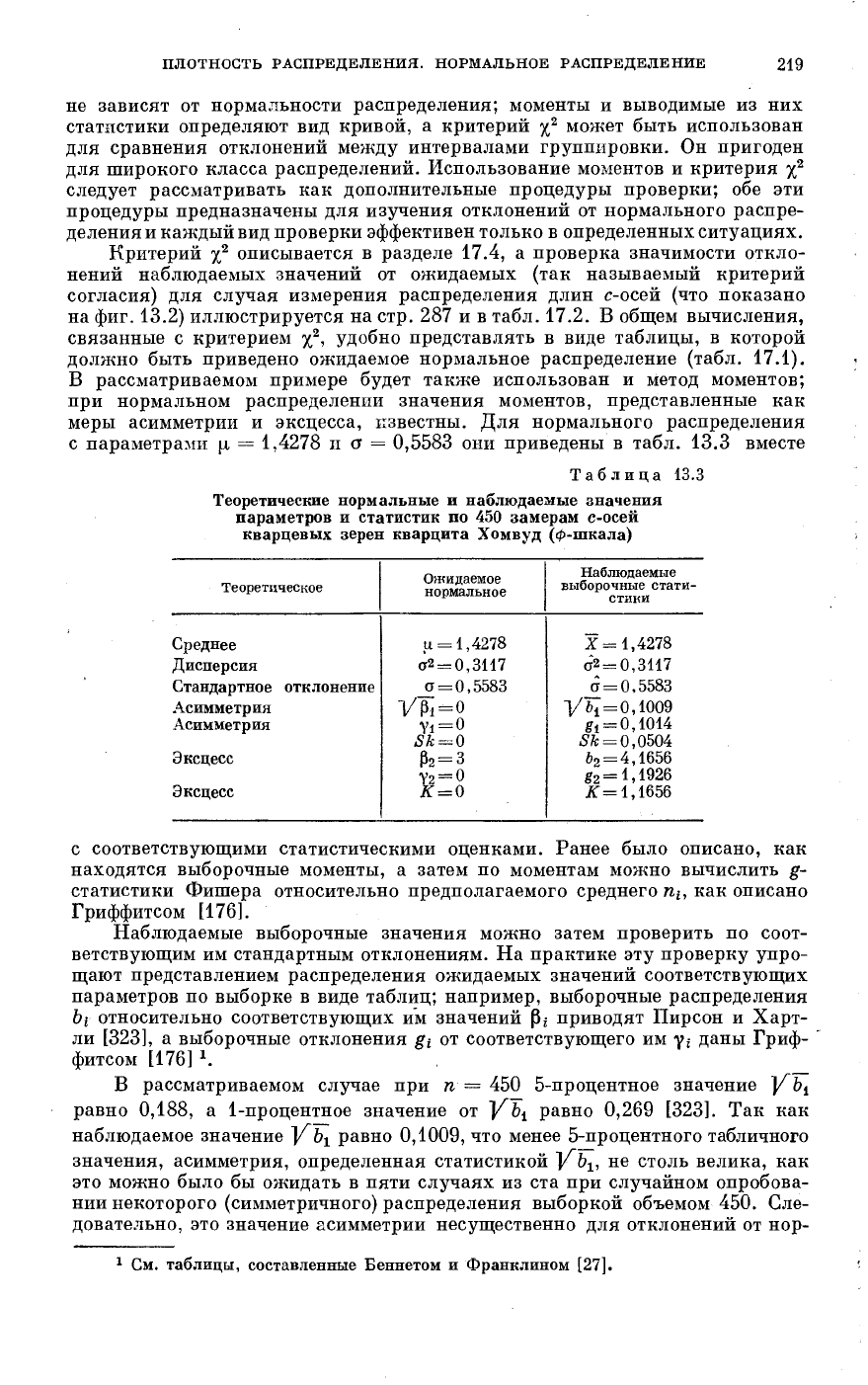
(фиг. 13.3). Тогда наблюдаемое

распределение можно наложить на вероятностную бумагу и расхождения

между ними легко заметить. На фиг. 13.3 имеется незначительное отклоне-

ние от основной тенденции, недостаточность на концах кривой и эксцесс

в области больших значений (например, 0ф и недостаток в области малых

значений, за исключением 2,5ф).

Более строгую проверку значимости этих отклонений можно провести

с помощью метода моментов или критерия χ

(см. раздел 17.4). Эти критерии

Фиг.

осей с

13.3. Функция распределения коротких

кварцевых зерен кварцита Хомвуд, нане-

сенная на ф-вероятностную бумагу.

1 — ожидаемые; 2 — наблюдаемые.

ПЛОТНОСТЬ РАСПРЕ ДЕЛЕ HHH

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

219

не зависят от нормальности распределения; моменты и выводимые из них

статистики определяют вид кривой, а критерий χ

может быть использован

для сравнения отклонений между интервалами группировки. Он пригоден

для широкого класса распределений. Использование моментов и критерия χ

следует рассматривать как дополнительные процедуры проверки; обе эти

процедуры предназначены для изучения отклонений от нормального распре-

деления и каждый вид проверки эффективен только в определенных ситуациях.

Критерий χ

описывается в разделе 17.4, а проверка значимости откло-

нений наблюдаемых значений от ожидаемых (так называемый критерий

согласия) для случая измерения распределения длин с-осей (что показано

на фиг. 13.2) иллюстрируется на стр. 287 и в табл. 17.2. В общем вычисления,

связанные с критерием χ

, удобно представлять в виде таблицы, в которой

должно быть приведено ожидаемое нормальное распределение (табл. 17.1).

В рассматриваемом примере будет также использован и метод моментов;

при нормальном распределении значения моментов, представленные как

меры асимметрии и эксцесса, известны. Для нормального распределения

с параметрами μ = 1,4278 π σ = 0,5583 они приведены в табл. 13.3 вместе

Таблица 13.3

Теоретические нормальные и наблюдаемые значения

параметров и статистик по 450 замерам с-осей

кварцевых зерен кварцита Хомвуд (ф-шкала)

Теоретическое

Ожидаемое

нормальное

Наблюдаемые

выборочные стати-

стики

Среднее

Дисперсия

Стандартное отклонение

Асимметрия

Эксцесс

μ = 1,4278

02 = 0,3117

_σ = 0,5583

YI=O

Sk = 0

= 3

= O

K = о

X = 1,4278

σ2 = 0,3117

_σ = 0,5583

= 0,1009

= 0,1014

Sfc =

0504

= 4,1656

= 1,1926

K= 1,1656

с соответствующими статистическими оценками. Ранее было описано, как

находятся выборочные моменты, а затем по моментам можно вычислить g-

статистики Фишера относительно предполагаемого среднего Ti

, как описано

Гриффитсом [176].

Наблюдаемые выборочные значения можно затем проверить по соот-

ветствующим им стандартным отклонениям. На практике эту проверку упро-

щают представлением распределения ожидаемых значений соответствующих

параметров по выборке в виде таблиц; например, выборочные распределения

bt относительно соответствующих им значений β, приводят Пирсон и Харт-

ли [323], а выборочные отклонения gi от соответствующего им даны Гриф-

фитсом [176] _

В рассматриваемом случае при η = 450 5-процентное значение J^b

равно 0,188, а 1-процентное значение от ]^b

равно 0,269 [323]. Так как

наблюдаемое значение ^b

равно 0,1009, что менее 5-процентного табличного

значения, асимметрия, определенная статистикой V^b

, не столь велика, как

это можно было бы ожидать в пяти случаях из ста при случайном опробова-

нии некоторого (симметричного) распределения выборкой объемом 450. Сле-

довательно, это значение асимметрии несущественно для отклонений от нор-

См. таблицы, составленные Беннетом и Франклином [27].

220

ГЛАВА 1 г

мального распределения. Мы можем заключить, что выборочное значение YT

соответствует оценке ΐ^βι = O- Аналогично, если серия из 450 наблюдений

является случайной выборкой из нормально распределенной совокупности,

в которой γ

= 0, значение g

равное 0,22 или больше, может ожидаться

в пяти случаях из ста [176]. Здесь также нет данных, которые бы свидетель-

ствовали об отклонениях от симметричного распределения по наблюдаемым

Теперь можно проверить эксцессивность, используя приближение: если

450 наблюдений представляют собой случайную выборку из нормальной

совокупности, то ожидаемые отклонения Ь

от теоретического значения β

(или g

от γ

) зафиксированы в соответствующих таблицах. Для такого зна-

чения β

при η = 450, 1-процентный уровень Ъ

равен 3,63; наблюдаемое же

значение Ъ

равно 4,1656, что значительно превышает 3,63. Аналогично ожи-

даемое по выборке значение g

равно 0,45 (приблизительно), в то время как

наблюдаемое значение равно 1,193, что опять же значительно. Из этого

можно заключить, что выборка имеет распределение, существенно отличаю-

щееся от нормального. Если вновь обратиться к фиг. 13.2, где ожидаемые

и наблюдаемые значения изображены графически, можно сказать, что здесь

действительно имеется существенное отклонение наблюдаемых значений

от ожидаемых в центральном классе и по краям кривой, но в целом кривая

достаточно симметрична относительно среднего значения.

Небезынтересно заметить, что при сравнении классов и судя по зна-

чению критерия χ

(см. табл. 17.1) такое отклонение можно ожидать реже,

чем один раз на 1000 таких выборок, и что это отклонение отражает влияние

эксцесса, превышающего эксцесс теоретического распределения.

Практически пришлось бы определить причину такого отклонения.

Можно полагать, что она отражает неслучайность отбора. Неясно, однако,

является ли эта неслучайность «естественной» или она вызвана действиями

исследователя при отборе зерен для измерений. Такую дилемму следует

решить до попытки сделать заключение о геологическом значении наблю-

даемого отклонения от нормального распределения.

При относительно небольшом η возможна приближенная проверка g-

критерием. Так как ожидаемые значения для и γ

в нормальном распре-

делении равны нулю, дисперсия выборочных значений g

относительно соот-

ветственных у( зависит исключительно от η [127, стр. 75]:

бге

(п — 1) _6_ .

(и— 2)(п+1)(л + 3) ~ л '

24» {η — I)

^ 24

(п — 3) (п

— 2)

(и + 3) (re-j-5) ~ η '

где η велико, скажем, более 1000.

Например, значения дисперсий в данном случае будут G

= 6/гс =

= 6/450 = 0,0133, σ|

= 24In = 24/450 = 0,0533; тогда Og

= 0,115 и σ|

=0,231. Используя отношения t = (X — μ)/σ, где (X — μ) — наблюдаемое

значение g, а σ — стандартное отклонение, получаем

0,1014

ооо.

0,231 -

163

из чего следует, что эксцесс является существенным, так как g

= 5,2.

Очевидно, что незначительно превышает (скажем, в два раза) свое

стандартное отклонение, тогда как g

значительно больше, чем удвоенное

стандартное отклонение. Одно из преимуществ g-критериев в том, что при

больших выборках они нормально распределены с соответствующими значе-

ниями γ, а площади, ограниченные нормальными кривыми, можно исполь-

зовать для приближенной оценки их значения [27].

ПЛОТНОСТЬ РАСПРЕ ДЕЛЕ HHH

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 221

13.7. НЕКОТОРЫЕ ОСОБЕННОСТИ НОРМАЛЬНОГО РАСПРЕДЕЛЕНИЯ

Нормальное распределение имеет множество свойств, которые чрез-

вычайно ценны для экспериментатора, так что во многих случаях стоит

потратить время на выбор приемов, приводящих к функции распределения

именно такого вида. В дополнение к сказанному о полезности строго опре-

деленной процедуры нормальное распределение, установленное однажды,

можно использовать следующим образом.

Средние арифметические, полученные по случайным выборкам из нор-

мальной совокупности со средним μ и стандартным отклонением σ, нор-

мально распределены со средним μ и стандартным отклонением а/Уп, где

η — объем выборки. Это· свойство может быть обобщено и строгое тре-

бование нормальности распределения может быть несколько ослаблено.

Если случайная величина X распределена со средним μ и стандартным

отклонением σ, для которого существует производящая функция моментов,

то величина t = (X - μ) Vnta распределена приблизительно нормально

со средним 0 и дисперсией, равной 1 при бесконечно большом η [198]. Другая

форма этого утверждения приводит к неравенству Чебышева и также дает

возможность существенно ослабить требования нормальности. Таким обра-

зом, если распределение произвольной совокупности имеет среднее μ и

конечную дисперсию σ

, распределение выборочного среднего приближается

к нормальному со средним μ и дисперсией σ

/η по мере возрастания объема

выборки [13]. Эта теорема

может быть выражена в форме вероятностного

утверждения:

Ρ(|Χ-μ|>δσ)<-^

Иначе говоря, вероятность того, что абсолютное значение отклонения X — μ

превысит в δ раз (δ — некоторая постоянная) стандартное отклонение σ,

1 с

менее или равна \ уменьшая о, можно контролировать вероятность откло-

нения.

Таким образом, при нормальном распределении со средним μ и диспер-

сией σ

P (I Χ—μ

> 2σ) = 0,05,

поскольку при снижении требований к нормальности и требований к строго

ограниченной дисперсии эта формула принимает вид

Ρ(|Χ-μ|>2σ) = ^- = 0,25.

Потеря эффективности в этом случае значительна, но чем меньше извест-

но о характере наблюдений, тем больше цена, которой дается их интерпре-

тация.

Упомянутая теорема, приводящая к неравенству Чебышева, практиче-

ски означает следующее: несмотря на то что случайная величина может быть

распределена и не нормально, если она не особо специфический тип, в котором

второй момент не конечен, случайные выборки из этой совокупности дадут

среднее арифметическое, имеющее тенденцию к нормальному распределению

по мере возрастания размеров выборки. По выборке, например равной 50

наблюдениям, в ряде случаев будет получена уверенность, что ее среднее

распределено почти нормально [198].

Функция нормального распределения дается в табл. 13.4. Если вместо

случайной величины X рассматривается выборочное среднее X, можно исполь-

зовать μ и σ/j/Vi; сузив, таким образом, интервал μ + к (alV~n), можно уве-

* Центральная предельная теорема, или закон больших чисел.