Гриффитс Дж. Научные методы исследования осадочных пород

Подождите немного. Документ загружается.

232

ГЛАВА 1 г

Интересно отметить, что, если логарифмы размеров действительно

нормально распределены, любая линейная комбинация нормальных слу-

чайных величин является также нормально распределенной; например,

если предположить, что объем F частиц неправильной формы выражен функ-

цией осей α-, Ъ-, и с-частицы,

F = abc,

IogF: то

Если log α, log b и log с нормально распределены, нормально распределен

и log F. Такая зависимость позволяет устанавливать отношения между

логарифмом объема и величиной измерений осей частиц в ф-единицах; изме-

нения логарифма объема тесно связаны с изменениями осей [181].

Аналогично Сичель [396], Росс [368] и Крайг [238] установили, что

логнормальная модель пригодная для характеристики распределения

в выборках из небольших навесок золота.

До сих пор, главным образом вследствие недостаточности объемов выбо-

рок и должного внимания к проблеме обеспечения случайности отбора,

остается не доказанным утверждение, согласно которому логнормальное

распределение является наилучшей моделью распределения элементов-при-

месей в земной коре [4, 62, 297, 299]. В настоящее время можно сказать, что

модель распределения, наиболее пригодная для характеристики распределе-

ния элементов-примесей, скорее является пуассоновой, нежели логнормаль-

ной (см. раздел 14.4 и последующие), и, чтобы решить вопрос, какая

из моделей «наилучшая», необходимо всесторонне исследовать распреде-

ление немногих представительных элементов с очень тщательным контролем

системы отбора для уверенности в полной случайности выбора из «однород-

ных совокупностей». До выполнения этого требования интерпретация харак-

тера распределения элементов-примесей будет оставаться объектом неиз-

вестной степени неточности

[435].

13.13. АЛЬТЕРНАТИВНАЯ МОДЕЛЬ

Предположим, что распределение размеров частиц оказалось не лог-

нормальным. Тогда можно предположить, что распределение средних зна-

чений логарифмов по выборкам не схо-

дится к нормальному, как это требует-

ся согласно центральной предельной

теореме. Вполне возможно объяснить

эту небходимость тем, что совокупность

зерен, которые образуют «естественную»

подсовокупность (т. е. пласты и про-

слойки, или, более точно, седимента-

ционные единицы [14, 317]), была вы-

брана не случайно: эта совокупность,

систематически смещенная от исходной

совокупности выборкой, остается тем

не менее логнормальной. G другой сто-

роны, рекомендуем изучить также аль-

тернативную модель, которая охваты-

вает и эту ситуацию.

Предположим, что случайная переменная, представляющая логарифм

размера частицы, является отношением двух случайных переменных, рас-

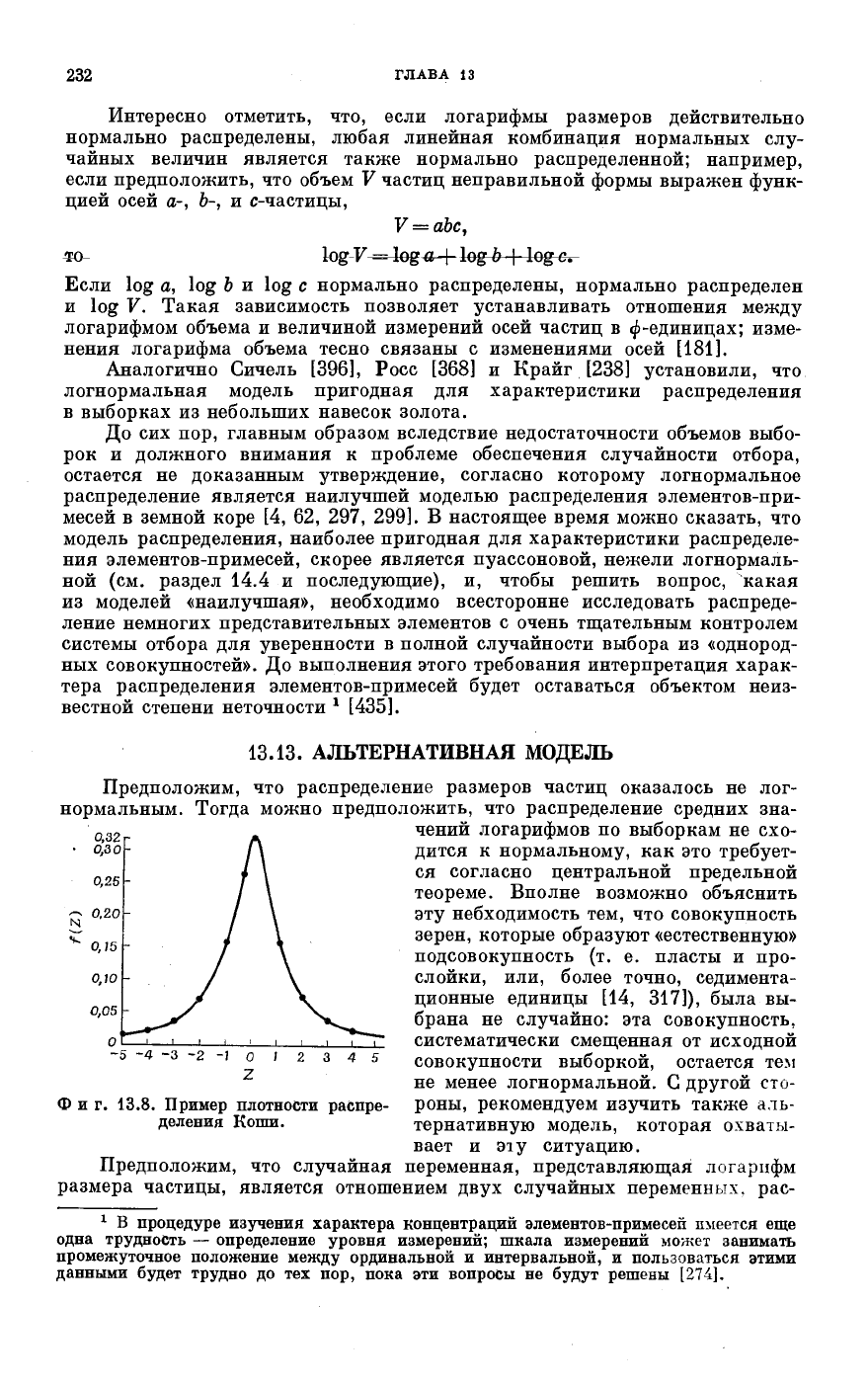
Ф и г. 13.8. Пример плотности распре-

деления Коши.

В процедуре изучения характера концентраций элементов-примесей имеется еще

одна трудность — определение уровня измерений; шкала измерений может занимать

промежуточное положение между ординальной и интервальной, и пользоваться этими

данными будет трудно до тех пор, пока эти вопросы не будут решены [274].

ПЛОТНОСТЬ РАСПРЕ ДЕЛЕ HHH

НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

233

пределенных нормально:

X = !-2- И

= ·

σ*

Тогда, если хну выбраны случайно, переменная z = x!y обладает распре-

делением Коши:

/<*) = 1йГнЗ) ' <z< + oo.

Для этого распределения среднее, подсчитанное по выборке, размером п,

не лучше единичного наблюдения для оценки значения среднего всей сово-

купности μ; медиана служит оценкой максимального правдоподобия цент-

ральной тенденции и не существует момента более высокого порядка, чем

первый; в частности, случайная величина является неопределенной и цент-

ральная предельная теорема неприложима. Кривая распределения частот

Коши показана на фиг. 13.8, и ее внешнее сходство с кривой нормального

распределения очевидно.

Случайные величины, имеющие распределение, выражаемое функцией

Коши, встречаются не так часто, как те, распределение которых прибли-

жается к нормальному, биномиальному, пуассоновому и т. д., но они все

же существуют. Всякий раз, когда ожидается, что данная переменная выра-

жает отношение двух случайных величин, можно убедиться в том, что если

они распределены нормально, то распределение той, которая представляет

их отношение, лучше всего описывается функцией Коши.

Одно из главных неудобств применения модели Коши заключается

в трудности оценки из-за недостаточной сходимости и неприменимости цент-

ральной предельной теоремы.

Г Л А В А 14

Дискретные распределения—биномиальное,

Пуассона и т. д.

...будут, рассмотрены следующие ситуации:

1. Рассматривается содержательно воспроизводимый эксперимент, ре-

зультатом которого может быть или S, или F [S — успех, F —

неудача].

2. В любом случае проведения эксперимента тот или иной результат

получается с некоторой долей вероятности; вероятность Получения

результата S равна Р, т. е. P (S) = р, a P (F) =1 — ρ = q.

3. Выполняется η независимых постановок эксперимента и фиксируется

количество испытаний с результатом S.

Таковы три условия, определяющие биномиальную модель.

P. J.McCarth у, Introduction to Statistical Reasoning, McGraw-

Hill Book Co., p. 177, 1957

14.1. ВВЕДЕНИЕ

Нормальное распределение является той моделью, которая наиболее

часто используется при обработке результатов измерений, главным образом

потому, что оно наиболее подходит как модель распределения непрерывных

случайных величин. В экспериментах другого типа основная операция состоит

в разбивке объектов по дискретным классам, сопровождаемой подсчетом

частот отнесения объектов к каждому из классов. Следовательно, здесь

пользуются дискретной шкалой, а в таких случаях более подходящими счи-

таются те модели, которые допускают использование такой шкалы.

В нашем распоряжении есть множество моделей распределения, кото-

рые могут быть использованы в различных ситуациях; это биномиальная

модель, модель Пуассона, отрицательная биномиальная и распределение,

а также модели заражения; все они могут рассматриваться в качестве под-

ходящих для пересчета данных наблюдений, разделенных на классы. Эти

модели использовались при изучении выборочных распределений минералов

при изучении минерального состава методом точечного подсчета в шлифах,

при изучении соотношений акцессорных минералов в тяжелой фракции и т. п.

1171, 174].

14.2. БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ

Формула разложения бинома хорошо известна и обычно записывает-

ся как

СΡ+9)

=Ρ

+πρ

-γ+^^ρ

-у+... +^pY-'. (14.1)

Это выражение, соответственно интерпретированное, удобно для под-

счета количества событий определенного рода, и этот подсчет можно произ-

вести чисто алгебраически. Однако в качестве вероятностного распределе-

ния его, возможно, лучше выразить в такой экспериментальной ситуации,

какую представляет собой описание частоты выпадения сторон подбрасы-

ваемой монеты. Обозначим случай выпадения решетки как S. Выпадения

ДИСКРЕТНЫЕ РАСПРЕДЕЛЕНИЯ — БИНОМИАЛЬНОЕ* ПУАССОНА И Т. Д. 235

герба или решетки — два единственно возможных исхода эксперимента;

вероятности каждого из этих событий равны, поэтому их можно записать

1 1

в виде бинома (р + q)

= (-g "g)*

· Вероятность одного из событий, таким

образом, будет ρ = 0,5, а вероятность противоположного события

l—p =

= 0,5.

Теперь будем подбрасывать две монеты; соответствующий бином будет

(р + q)

— (0,5 + 0,5)

, где η — количество бросков. Возможные исходы

положения подброшенных монет даны в табл. 14.1; принимая во внимание

Таблица 14.1

Частота выпадения гербов при подбрасывании двух монет

—

герб; P

—

решетка

Исходы

Вероятность

Число

выпадений

герба

Частота

1 2

Вероятность

Число

выпадений

герба

исходов

Г г

1 1 1

2 ~ 4

Г P

2 2

—

1 2

P г

2 2 ~ 4

P P

1 1 1

2 ~~ 4

частоту появления решетки, это можно выразить так: частота одновремен-

ного выпадения решеток — 1, решетки и герба — 2 (независимо от порядка

монет) и двух гербов — 1.

В табл. 14.2 подсчитаны результаты подбрасывания четырех монет,

однако для большого количества подбрасываемых монет трудность под-

счета быстро возрастает. Разложение соответствующих биномов упрощает

расчет:

n = lp + q

ra = 2p

+ 2pg + g

η = Зр

+ 3 p

q +

3pq*

+ q

η = 4p

+ 4p

q + 6 pV + 4pq

и, если коэффициенты членов разложения представить в форме треуголь-

ника Паскаля, правило подсчета становится весьма ясным:

1 1

1 2 1

13 3 1

1 4 6 4 1

1 5 10 10 5 1

1 6 15 20 15 6 1

Возможность применения этой процедуры, однако, ограничена теми

случаями, когда вероятность события, скажем выпадения «решетки» при

бросании монеты (или в более общем примере «успех»), равна вероятности

противоположного события. Так, вероятность выпадения 5 на игральной

236

ГЛАВА 1 г

Таблица 14.2

Частота выпадений гербов при подбрасывании четырех монет

—

герб; P

—

решетка

Исходы

Вероятность выпадения

гербов

Число

выпадения

гербов

Частота

неходов

2 3 4

Вероятность выпадения

гербов

Число

выпадения

гербов

Частота

неходов

Ш'ШЧ

г P

Ш'ШН

P г

Шт)'-А

P г

(т ΠΑ'-έ

3 4

P г г

(тШ'-i

P г

(т)'(т)Ч

(тШЧ

2 6

г P

АТУ-К

Ш'ШЧ

г г

г P

P 1

Шт)Ч

Шт)-и

1 4

P P г

Ш'ШЧ

P P

ШЧт)Н

кости равна 1/6, а вероятность невыпадения — 5/6. Это приводит к несим-

метричной биномиальной форме, и подсчет вероятностей несколько услож-

няется. Но разложение соответствующих биномов можно использовать

и в данном роде экспериментов, так что правила для нахождения коэффициен-

тов разложения бинома приводят к возможности установления частоты собы-

тий. Общая форма разложения —

= У, (14.2),

где C

— количество сочетаний из η по г и представляет собой коэффициент,

обозначающий частоту встречаемости события г раз; р

— вероятность

встречи события, a q

— вероятность того, что данное событие не про-

изойдет.

ДИСКРЕТНЫЕ РАСПРЕДЕЛЕНИЯ — БИНОМИАЛЬНОЕ* ПУАССОНА И Т. Д. 237

Предположим, что цель эксперимента — подсчет количества зерен цир-

кона в тяжелой фракции или количества зерен кварца по заданной линии

в шлифе. Известно, что число появлений данного события (зерна циркона

или точек, попавших на кварц) распределено биномиально с ρ — 0,4 и что

яо линии расположено 5 зерен (или точек наблюдения) и нам нужно узнать

распределение вероятностей встречи того или иного исхода (зерна циркона

или кварца). В целом намечается рассмотреть 1000 (N) линий, пересекающих

по 5 (га) точек наблюдений (или зерен), и требуется определить теоретиче-

скую или предполагаемую плотность распределения числа появления собы-

тия (кварц или цирконовое зерно) на каждой линии по всем 1000 пересече-

ниям. Подходящий для этой цели бином будет

N (р + q)

= 1000 (0,4 + 0,6)

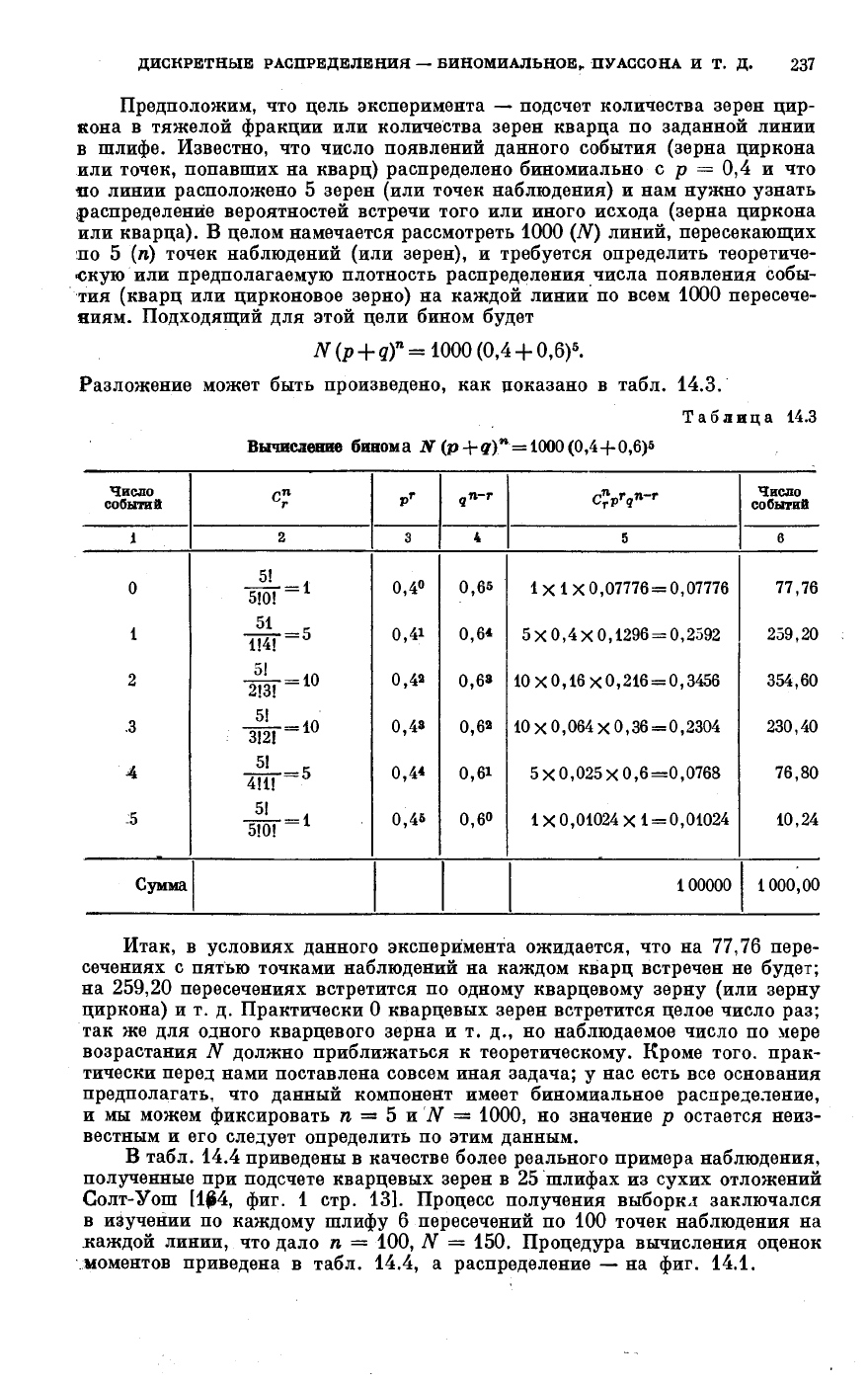
Разложение может быть произведено, как доказано в табл. 14.3.

Таблица 14.3

Вычисление бинома JV (р + q)

= 1000 (0,4 + 0,6)5

Число

событий

с™

п-г

Число

событий

-1

5!0!

0,4°

0,65

Ix 1x0,07776 = 0,07776

77,76

1!4!

0,41 0,6*

5x0,4x0,1296 = 0,2592

259,20

2!3!-

0,42

0,63

10 x 0,16 x 0,216 = 0,3456 354,60

зm-

0,43

0,62

10 x 0,064 x 0,36 = 0,2304 230,40

4!1! ~

0,4« 0,61 5 x 0,025 x 0,6 = 0,0768

76,80

-1

5!0!

0,4в

0,6"

1X0,01024X1=0,01024

10,24

Сумма 100000

1000,00

Итак, в условиях данного эксперимента ожидается, что на 77,76 пере-

сечениях с пятью точками наблюдений на каждом кварц встречен не будет;

на 259,20 пересечениях встретится по одному кварцевому зерну (или зерну

циркона) и т. д. Практически 0 кварцевых зерен встретится целое число раз;

так же для одного кварцевого зерна и т. д., но наблюдаемое число по мере

возрастания N должно приближаться к теоретическому. Кроме того, прак-

тически перед нами поставлена совсем иная задача; у нас есть все основания

предполагать, что данный компонент имеет биномиальное распределение,

и мы можем фиксировать η = 5 и N — 1000, но значение ρ остается неиз-

вестным и его следует определить по этим данным.

В табл. 14.4 приведены в качестве более реального примера наблюдения,

полученные при подсчете кварцевых зерен в 25 шлифах из сухих отложений

Солт-Уош [1#4, фиг. 1 стр. 13]. Процесс получения выборкл заключался

в изучении по каждому шлифу 6 пересечений по 100 точек наблюдения на

каждой линии, что дало га = 100, N = 150. Процедура вычисления оценок

моментов приведена в табл. 14.4, а распределение — на фиг. 14.1.

238

ГЛАВА 1 г

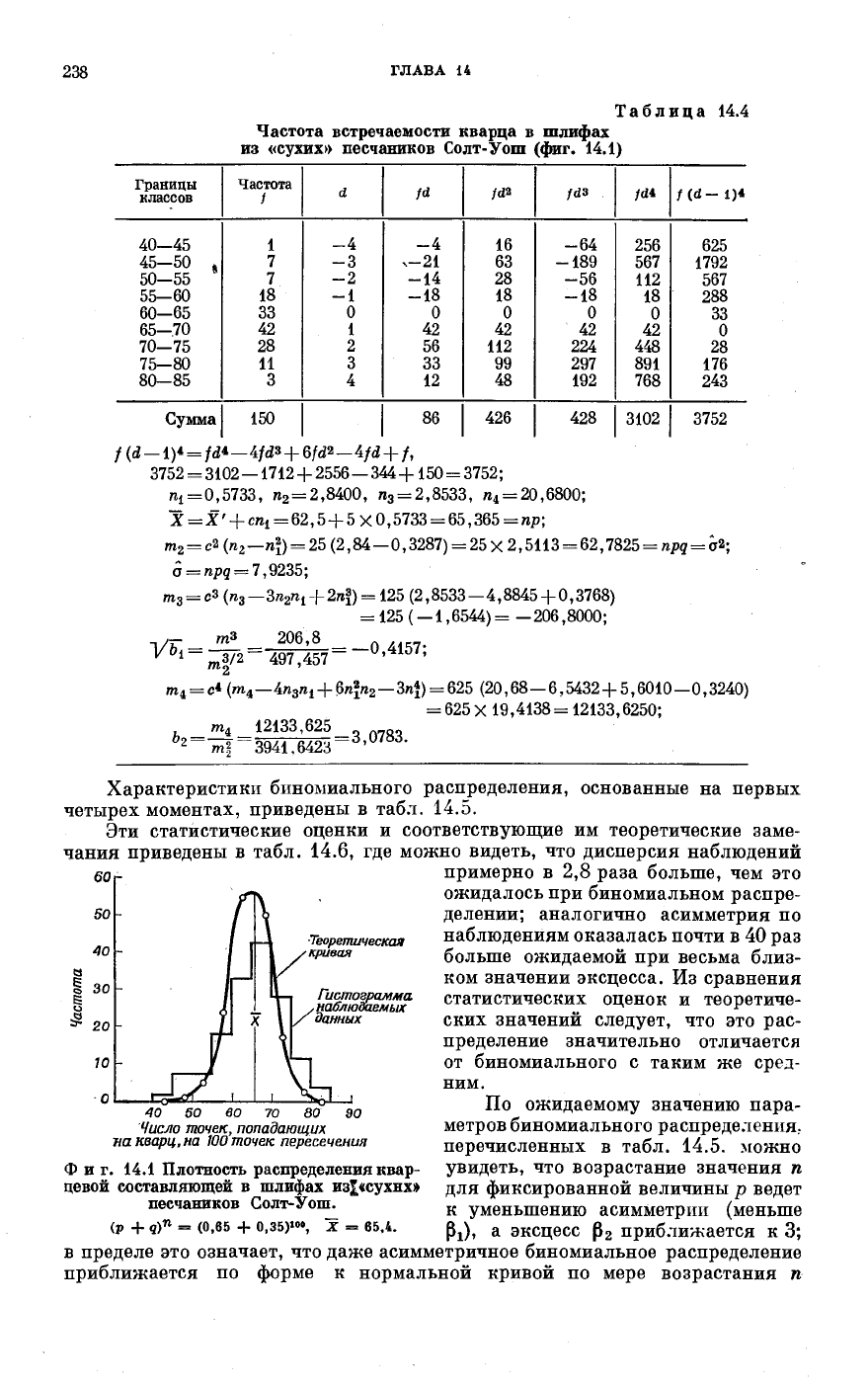
Таблица 14.4

Частота встречаемости кварца в шлифах

из «сухих» песчаников Солт-Уош (фиг. 14.1)

Границы

классов

Частота

fd 2

fd3

fd*

Hd- 1)*

40—45

-4 -4

16 -64

256

625

45-50

-3

V-21 63

-189 567

1792

50-55

-2 -14

-56

112

567

55-60

-1

-18 18 -18

288

60-65

0 0

65-70 42

1 42 42 42

70-75

28 2

112 224 448

75-80 И

3 33 99

297 891

176

80—85 3

12 48

192 768

243

Сумма

150 86

426

428

3102

3752

/ (d —

1)*

= fd*—ifds + 6/da _ 4fd + /,

3752 = 3102—1712 + 2556—344 +150 = 3752;

= 0,5733,

тг

= 2,8400, га

= 2,8533, ге

= 20,6800;

X = X' +

Cre

= 62,5 +5 χ 0,5733 = 65,365 = пр;

(в

_ п|) = 25 (2,84—0,3287) = 25 χ 2,5113 = 62,7825 = npq =

a = npq = 7,9235;

= сЗ (и

— Sti

2га?)

= 125 (2,8533—4,8845 + 0,3768)

= 125(-1,6544)=-206,8000;

т з 206,8

'=;^p== 497^57

4157;

с*

-An

+ 6ге*ге

—3raJ) = 625 (20,68

—

6,5432 + 5,6010 —0,3240)

12133,625

= = 3941.6423

= 3

0783

625

χ 19,4138 = 12133,6250;

Характеристики биномиального распределения, основанные на первых

четырех моментах, приведены в табл. 14.5.

Эти статистические

чания приведены в табл.

60 г

•Теоретическая

кривая

Гистограмма,

наблюдаемых

Число точек,

попадающих

Ήα

кварц, на

100 точек

пересечения

Фиг. 14.1 Плотность распределения квар-

цевой составляющей в шлифах из|«сухнх»

песчаников Солт-Уош.

оценки и соответствующие им теоретические заме-

14.6, где можно видеть, что дисперсия наблюдений

примерно в 2,8 раза больше, чем это

ожидалось при биномиальном распре-

делении; аналогично асимметрия по

наблюдениям оказалась почти в 40 раз

больше ожидаемой при весьма близ-

ком значении эксцесса. Из сравнения

статистических оценок и теоретиче-

ских значений следует, что это рас-

пределение значительно отличается

от биномиального с таким же сред-

ним.

По ожидаемому значению пара-

метров биномиального распределения,

перечисленных в табл. 14.5. можно

увидеть, что возрастание значения η

для фиксированной величины ρ ведет

к уменьшению асимметрии (меньше

), а эксцесс β

приближается к 3;

(Р + Ч)

= (0,65 + 0,35)"·, X = 65.4.

в пределе это означает, что даже асимметричное биномиальное распределение

приближается по форме к нормальной кривой по мере возрастания η

ДИСКРЕТНЫЕ РАСПРЕДЕЛЕНИЯ — БИНОМИАЛЬНОЕ* ПУАССОНА И Т. Д. 239

(или Ν). Пример с распределением кварцевых зерен в песчаниках Солт-Уош

показывает, что даже при ρ Φ 0,5, например ρ = 0,654 и N = 150, ожи-

Таблица 14.5

Сводка статистик и параметров биномиальной

плотности распределения

(14.3)

(14.4)

(14.5)

(14.6)

даемая асимметрия близка к нулю, а ожидаемый эксцесс близок к трем.

В общем по мере возрастания /г] (и /или N) биномиальное распределение

Таблица 14.6

Наблюдаемые и теоретические сводные статистики

для плотности распределения кварца в сухих

песчаниках Солт-Уош

Статистики Теоретические. Наблюдаемые

Среднее= μ = пр

Дисперсия = σ

= npq

iq п)2

Асимметрия = βι = ^

Эксцесс-β

=3+

1_6р?

npq

65,37

22,6284

0,0042

65,37

62,7825

0,1728

Среднее= μ = пр

Дисперсия = σ

= npq

iq п)2

Асимметрия = βι = ^

Эксцесс-β

=3+

1_6р?

npq

2,9842 3,0783

будет приближаться к нормальному, и при сопоставлении наблюдаемых

частот с ожидаемыми можно использовать, как описывалось выше

(см. раздел 13.5), таблицу площадей для нормального распределения

14.3. СОГЛАСОВАНИЕ НАБЛЮДАЕМЫХ ЧАСТОТ

С ФУНКЦИЕЙ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ

Когда выполнено некоторое количество экспериментальных наблюдений

и количество успешных событий разнесено по классам: «нулевой успех»,

«один успех», «два успеха» и т. д., то наблюдаемое распределение можно аппро-

ксимировать биномиальной функцией. Условия, в которых биномиальное

распределение будет подходящей моделью для описания серии наблюдений,

следующие:

1. Исход испытаний классифицируется или как успех, или как неудача; например,

при подсчете числа зерен циркона в тяжелой фракции исход каждого наблюдения клас-

сифицируется как циркон (успех) или не циркон (неудача).

2. Испытания независимы, т. е. присутствие циркона в каждой следующей точке

наблюдения не зависит от того, был ли циркон в предыдущей точке и т. д.

3. Вероятность обнаружения циркона постоянна в каждой точке.

В данном*случае речь идет не о дискретной случайной величине, а о ее функции

та—пр „ . , „

t — - , где

тп

— число появлении события в] серии щ испытании. Распределение

№

—Р)

t с ростом η будет приближаться к нормальному с параметрами 0,1.— Прим. ред.

Среднее = μ = пр

Дисперсия =

= npq

tq р)2

Асимметрия = βι = ———

npq

Эксцесс = β

= 3+—'

npq

240

ГЛАВА 1 г

При исследовании частот обнаружения циркона в тяжелой фракции

генеральная совокупность представляет собой все множество зерен в пре-

парате или же по какому-либо пересечению, и, если фракция приготовлена

с соблюдением всех правил, циркон в ней будет распределен случайно. Наблю-

дения, производимые по некоторой линии, пересекающей η зерен, которые

классифицируются как «циркон» и «не циркон», будут фиксировать случайное

распределение циркона, а вероятность его обнаружения при переходе от зерна

к зерну будет постоянной. Допустим, что произведены наблюдения по N

таких пересечений. Тогда каждое пересечение даст некоторую оценку p

вероятности обнаружения циркона в препарате. Наблюдаемые р

будут

группироваться около некоторого центрального значения р, которое явля-

ется оценкой истинной пропорции P циркона в препарате. В таких условиях

проверка согласованности наблюдаемого распределения с биномиальным

Анализ

Микроразделвнае

Экспериментам- приемник в

эфирно» масле

ная

процедура

^ >| j ^ \ ^ ^

Тяжелая ,,

фракция

На

хранение

Линии

пересечений

1-Вч

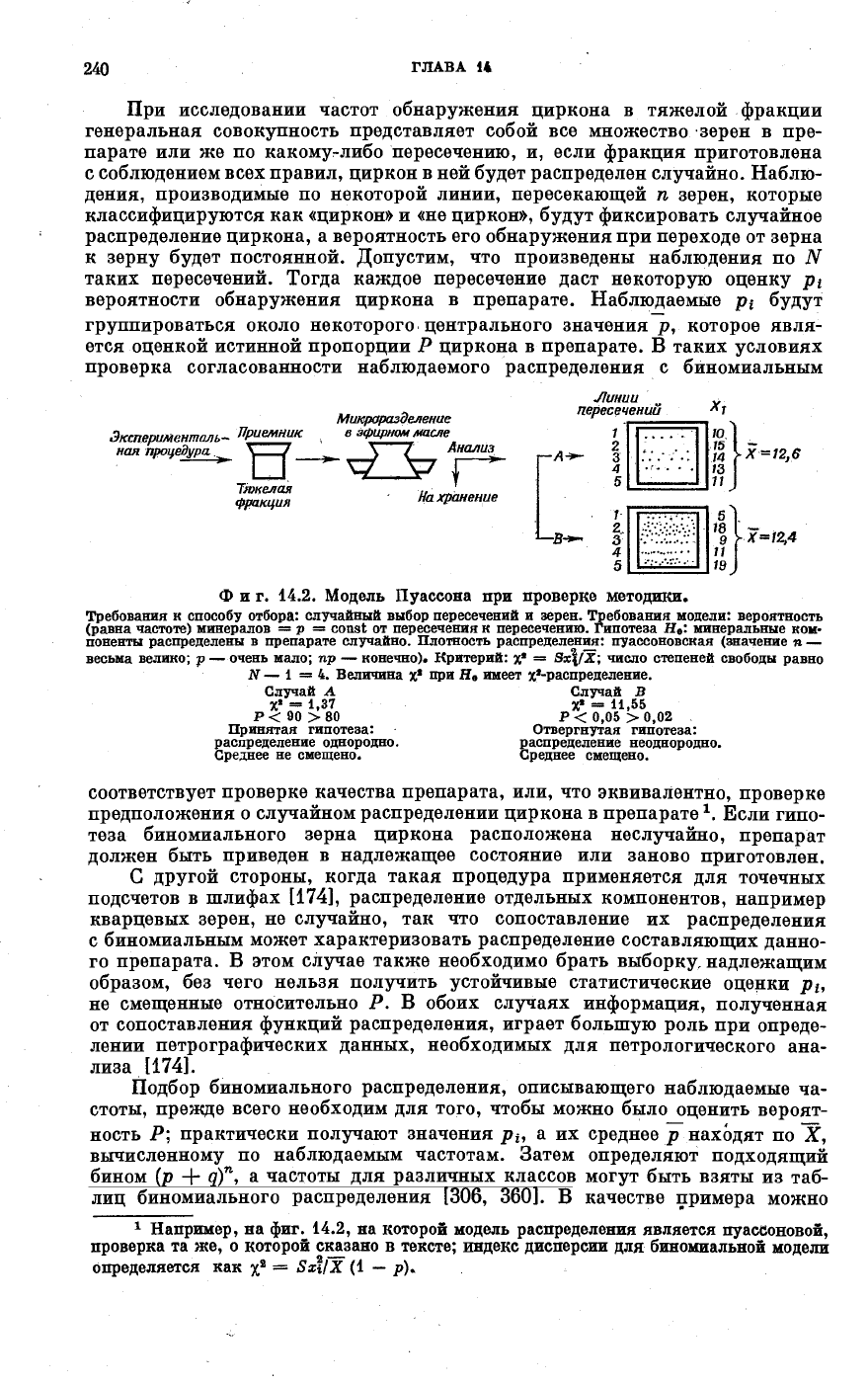
Фиг. 14.2. Модель Пуассона при проверке методики.

Требования к способу отбора: случайный выбор пересечений и зерен. Требования модели: вероятность

(равна частоте) минералов = ρ = const от пересечения к пересечению, гипотеза H

: минеральные кои-

поненты распределены в препарате случайно. Плотность распределения: пуассоновская (значение η —

весьма велико; ρ — очень мало; пр — конечно). Критерий: χ» = Sx\/X\ число степеней свободы равно

N — 1 =4. Величина χ« при Я

имеет χ'-распределение.

Случай А Случай В

= 1,37 χ" = 11,55

P < 90 > 80 P < 0,05 > 0,02

Принятая гипотеза: Отвергнутая гипотеза:

распределение однородно. распределение неоднородно.

Среднее не смещено. Среднее смещено.

соответствует проверке качества препарата, или, что эквивалентно, проверке

предположения о случайном распределении циркона в препарате Если гипо-

теза биномиального зерна циркона расположена неслучайно, препарат

должен быть приведен в надлежащее состояние или заново приготовлен.

С другой стороны, когда такая процедура применяется для точечных

подсчетов в шлифах [174], распределение отдельных компонентов, например

кварцевых зерен, не случайно, так что сопоставление их распределения

с биномиальным может характеризовать распределение составляющих данно-

го препарата. В этом случае также необходимо брать выборку, надлежащим

образом, без чего нельзя получить устойчивые статистические оценки pi,

не смещенные относительно Р. В обоих случаях информация, полученная

от сопоставления функций распределения, играет большую роль при опреде-

лении петрографических данных, необходимых для петрологического ана-

лиза [174].

Подбор биномиального распределения, описывающего наблюдаемые ча-

стоты, прежде всего необходим для того, чтобы можно было оценить вероят-

ность Р; практически получают значения ρ ι, а их среднее ρ находят по X,

вычисленному по наблюдаемым частотам. Затем определяют подходящий

бином (р + (?)", а частоты для различных классов могут быть взяты из таб-

лиц биномиального распределения [306, 360]. В качестве примера можно

Например, на фиг. 14.2, на которой модель распределения является пуасеоновой,

проверка та же, о которой сказано в тексте; индекс дисперсии для биномиальной модели

Определяется как χ* = Sxi/X (1 - ρ).

ДИСКРЕТНЫЕ РАСПРЕДЕЛЕНИЯ — БИНОМИАЛЬНОЕ* ПУАССОНА И Т. Д. 241

взять частоту кварцевых зерен в песчаниках Солт-Уош, приведенную

в табл. 14.4. Из X — 65,365 в известной длине линии наблюдения с га = 100

имеем X = пр, где ρ = 0,654; подходящим биномом является (0,654 +

+ 0,346)

100

, а требующиеся частоты находим в работе Ромига [3601. Получа-

ется, что на 100 точек наблюдения по линии приходится 40 или менее квар-

цевых зерен. Далее проведем преобразование:

В(Х, га, р) =

1 —

В(п — χ— 1, п, q). (14.7)

В нашем случае

тг ==

100, ρ = 0,65, q = 0,35, что дает

В{Х\ 100; 0,65) = 1

— .В

(100 —я

—

1, 100, 0,35).

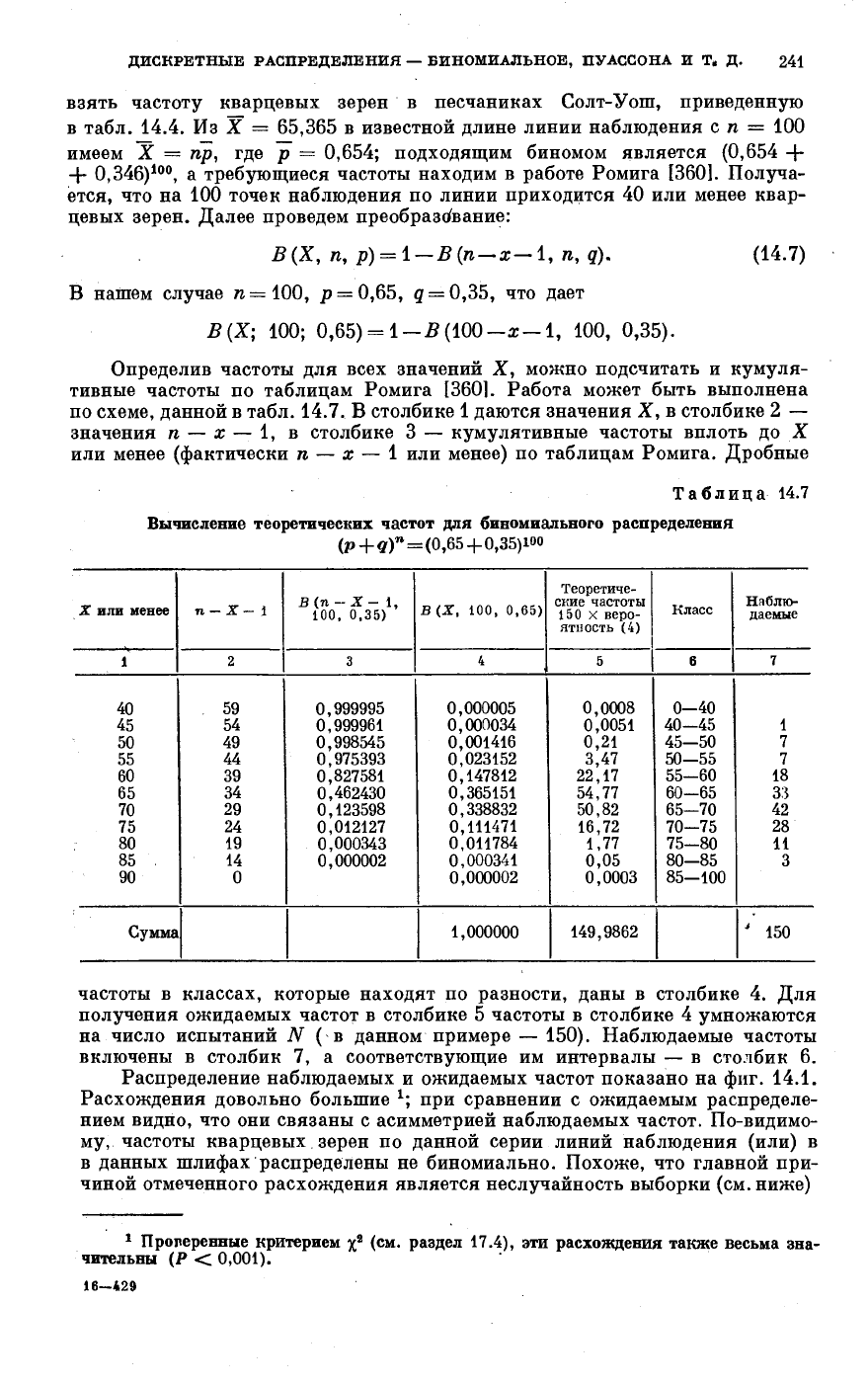
Определив частоты для всех значений X, можно подсчитать и кумуля-

тивные частоты по таблицам Ромига [360]. Работа может быть выполнена

по схеме, данной в табл. 14.7. В столбике 1 даются значения X, в столбике 2 —

значения га — χ — 1, в столбике 3 — кумулятивные частоты вплоть до X

или менее (фактически re — χ — 1 или менее) по таблицам Ромига. Дробные

Таблица 14.7

Вычисление теоретических частот для биномиального распределения

(р+ «0

= (0,65 + 0,35)Ю0

Теоретиче-

X или менее

—

X-l

В (η

—

В (X, 100, 0,65)

ские частоты

Класс

Наблю-

X или менее

—

X-l

100, 0,35)

В (X, 100, 0,65)

150 х веро-

Класс

даемые

ятность (4)

2 3

5 6

59 0,999995

0,000005

0,0008

0—40

0,999961 0,000034

0,0051

40-45

49 0,998545

0,001416 0,21 45—50

0,975393

0,023152 3,47

50—55

60 39

0,827581 0,147812 22,17 55-60

0,462430

0,365151 54,77

60-65 33

0,123598 0,338832

50,82 65-70 42

24 0,012127

0,111471

16,72 70-75

0,000343

0,011784

1,77

75-80

85 14 0,000002

0,000341

0,05

80—85

90 0

0,000002

0,000002 0,0003 85—100

Сумма 1,000000 149,9862

' 150

частоты в классах, которые находят по разности, даны в столбике 4. Для

получения ожидаемых частот в столбике 5 частоты в столбике 4 умножаются

на число испытаний N ( в данном примере — 150). Наблюдаемые частоты

включены в столбик 7, а соответствующие им интервалы — в столбик 6.

Распределение наблюдаемых и ожидаемых частот показано на фиг. 14.1.

Расхождения довольно большие

; при сравнении с ожидаемым распределе-

нием видно, что они связаны с асимметрией наблюдаемых частот. По-видимо-

му, частоты кварцевых зерен по данной серии линий наблюдения (или) в

в данных шлифах распределены не биномиально. Похоже, что главной при-

чиной отмеченного расхождения является неслучайность выборки (см. ниже)

Проверенные критерием χ

(см. раздел 17.4), эти расхождения также весьма зна-

чительны (Р < 0,001).

16—429