Гриффитс Дж. Научные методы исследования осадочных пород

Подождите немного. Документ загружается.

262

ГЛАВА 1 г

При измерениях формы зерен в шлифах средние значения длины и ширины

зерен в ф-единицах независимы от соответствующих ф-стандартных отклоне-

ний. Если измерения выражены на миллиметровой шкале и форма оценена

по двумерным графикам длинных и коротких осей, эти графики имеют дис-

персию, сильно зависящую от другой случайной величины [168, 181]. При

логарифмическом преобразовании встает дилемма: использовать ли отноше-

ние длинной оси к короткой (α/b) или же короткой к длинной (Ыа)? Во втором

случае интервал будет от 0 до 1, а в первом — от 1 до оо; оба отношения

содержат одну и ту же информацию и чаще всего используется отношение Ыа.

Распределение обычно приближается к нормальному, хотя иногда возни-

кают различные степени усечения, в частности эксцесс накопления частот

в классах, близких значению отношения Ыа = 1 (сечения круглых зерен).

Для ближайшего будущего подходящим аналитическим аппаратом пред-

ставляется в ф-преобразование для осей, а линейная, регрессионная, модель

(фиг. 6.8) — для описания соотношений между осями. При применении этих

процедур упорядочение осей на а> Ь, измеренных в миллиметрах (Ъ -< а

в ф-единицах), усекает двухмерный график. Это в свою очередь влияет на ко-

эффициент корреляции и приводит к корреляции, равной 0,66 для двухмер-

ного случя (Smith, личное сообщение). Но так как корреляция средних зна-

чений по малой выборке обычно ожидается как г = 0,75, некоторая связь

все же имеется, несмотря на псевдокорреляцию. Возможно, это и хорошо,

когда связь между длинными и короткими осями зерен действительно равна

нулю, в то время как связь между выборочными средними по мере увеличе-

ния количества зерен в выборке или количества выборок возрастает ([164]

и раздел 21.15).

Так как измерение осей зерен в шлифах фактически представляет про-

цедуру измерения «кажущихся» длинных и коротких осей, результат такой

работы основан на эмпирических данных и в каком-либо простом соотноше-

нии с фактическим (реально существующим) изменением формы может не вы-

разиться.

Когда измерения формы выполнены непосредственно на отдельных части-

цах породы, данные по всем трем осям — длинной а, средней Ъ и короткой

с — могут быть преобразованы от миллиметровой или микронной шкаЛы

к ф-единицам; тогда распределение размеров любой осп должно быть ф-

нормальным. Любое линейное сочетание этих данных измерений распреде-

лено также нормально, например коэффициент сферичности (эллипсоидаль-

ности) ф, рекомендованный Крамбейнод [252], определенный как

а после трансформации

и значение ф' тоже будет нормально распределенным, что подтверждается

эмпирическими исследованиями [81, 82]. Можно утверждать, что такие выбо-

рочные средние, как X и дисперсия σ

, будут независимы, что и видно на

фиг. 6.15. Однако, когда образцы группируются по петрографическим

свойствам на аркозы, субграувакки и кварциты, полученные средние и дис-

персии становятся зависимыми. В трех образцах аркозов, отобранных для

изучения источников сноса, расположенных недалеко от места переотложен-

ного материала, выборочные средние очень малы, в то время как дисперсия

весьма изменчива. С другой стороны, в трех образцах кварцитов, представ-

ляющих обломочный материал, перенесенный с далеко расположенного

источника сноса, дисперсии менее изменчивы, а колебания средних более

значительны. У субграувакк обнаружены промежуточные значения, в кото-

СВЯЗЬ МЕЖДУ СРЕДНИМ И ДИСПЕРСИЕЙ

263

рых наблюдается связь (в данном случае линейная) между средними и диспер-

сией. Эта зависимость, положенная в основу выборочной модели, представ-

ленной на фиг. 2.3, является отражением степени избирательной сортировки

tto форме, происходящей при переносе обломочного материала (кварца)

от питающей провинции к месту отложения. Что же касается взаимоотно-

шения между средним и дисперсией, то оно отражает различные степени

смещения, которое может быть использовано для характеристики различных

процессов образования обломочного материала. Иначе говоря, оно характе-

ризует фации.

Измерение степени окатанности тех же кварцевых зерен приводит к ана-

логичным зависимостям между средними значениями и дисперсиями, что

отражает те же процессы селективной сортировки. Вероятно, что данные

по окатанности. как это видно по результатам лабораторных экспериментов

«(см. раздел 6.7), более тонко отражают условия осадкообразования, чем

показатели сферичности.

В дальнейшем можно рекомендовать при исследовании формы

облом-

ков применять такой способ отбора, который помог бы ликвидировать как

различия между средними, так и дисперсионные взаимоотношения в преде-

лах подсовокупностей, если сходимость между подсовокупностями будет

значительной. Эта рекомендация равносильна рекомендации пользоваться

только случайными выборками, т. е. стремиться к тому, чтобы к выборочным

.данным могла быть применима равновероятностная модель.

15 4.3. Состав осадков и отсортированность по составу

Правила о взаимозависимости между средним и дисперсией можно рас-

сматривать как вравноценные вообще для любых переменных, так что поня-

тие о взаимосвязи по размерам и отсортированности по размерам не ограни-

чивается областью изучения только размеров зерен. Когда изучают изменение

-состава, при процедуре подсчета может оказаться, что модель дискрет-

ного распределения подходит и в этом случае. Если имеется к (к = 2) клас-

сов, то подходящим будет биномиальное распределение или распределение

Пуассона; когда же классов более 2 (к > 2), подходящей моделью можно

считать полиномиальные функции. Первый вид моделей, где соотношение

между средним и дисперсией довольно определенное, уже рассмотрен, также

рассмотрена и полиномиальная модель (см. раздел 14.10), где среднее связано

с дисперсией таким же способом, как и в биномиальной (см. стр. 250). Сле-

дует, однако, добавить, что ковариационные соотношения возникают между

разными классами и это усложняет обработку подобных данных. Чейс [56,

65>—67] описал влияние таких зависимостей на сравнения частот распреде-

ления состава двух или более классов, и, в частности, он подчеркнул, что

возможна ложная корреляция. Допустим, есть три переменные величины,

составляющие 100%, т. е. сумма постоянна; при этом условии, если частоты

любых двух величин возрастают, частота третьей должна убывать, что при-

водит к различным степеням отрицательной связи между этими переменными.

Из-за этой особенности изучать изменение состава без простейших количест-

венных сопоставлений очень трудно.

Ясно также, что монотонные преобразования эффективными не будут.

'Сейчас развитие теории информации [390] достигло уровня, допускающего

применение статистического анализа [272, 299], и энтропиеподобная функ-

ция Шеннона — Винера

H = -J

Pilogp

(15.4)

Такие же рекомендации по составлению выборок применимы для любых свойств,

^испытывающих влияние селективной сортировки, так что наши рекомендации являются

довольно общими.

264 ГЛАВА 1 г

может служить приемлемым преобразованием для анализа однотипных дан-

ных. В этом преобразовании могут быть использованы различные основания

логарифмов: 10, е или 2; последнее, будучи основанием бинарных шкал,

образует бинарные отношения, лежащие в основе вычислений на электронно-

вычислительных машинах. Кульбак [272] приводит таблицу plnp, облегчаю-

щую подобные преобразования при статистическом анализе. Применяя лога-

рифмы с основанием 2, для преобразованных данных можно давать непосред-

ственную меру информации в битах (недостаточную для двоичной системы);:

было предложено называть соответственно преобразованные данные нитами,

если в качестве основания логарифмов используется е, логитами, если осно-

ванием является 10 [283].

ф-преобразование, впервые предложенное Крамбейном [247], можно

представить как

d = 2-*,

где d

—

диаметр в миллиметрах; при преобразовании с основанием 2 это·

выражение превращается в

Iog

C?=- ф, в битах.

Следовательно, если применяются информационные преобразования

на основании логарифмов 2 по отношению к данным, представляющим изме-

нения состава и выраженным в процентах, то результаты преобразований

получаются в битах, т. е. в той же шкале, как и данные о размерах (и форме)·

зерен.

Применение теории информации в геологии впервые предложено Пел-

то [328]; некоторые примеры рассмотрены Миллером и Каном [299]; пример-

использования информационных преобразований для процентных данных

приведен Гриффитсом.

15.5. КОЭФФИЦИЕНТ ИЗМЕНЧИВОСТИ

Под другим аспектом рассмотрена зависимость между средним и дис-

персией, что требует использования коэффициента изменчивости CV, кото-

рый определяется как

CV% = IOO-^r ; (15.5).

он представляет частное от деления стандартного отклонения о на сред-

нее X в процентах. Коэффициент изменчивости обладает коварной привле-

кательностью вследствие кажущейся возможности сравнивать изменения

различных переменных независимо от вида применяемой шкалы, иначе

говоря, он безразмерен. Им можно пользоваться только в том случае, когда

основывающие его данные достигают уровня отношений (см. раздел 12.5),

но когда данные не достигают этого информационного уровня, применение

его может привести к ошибкам.

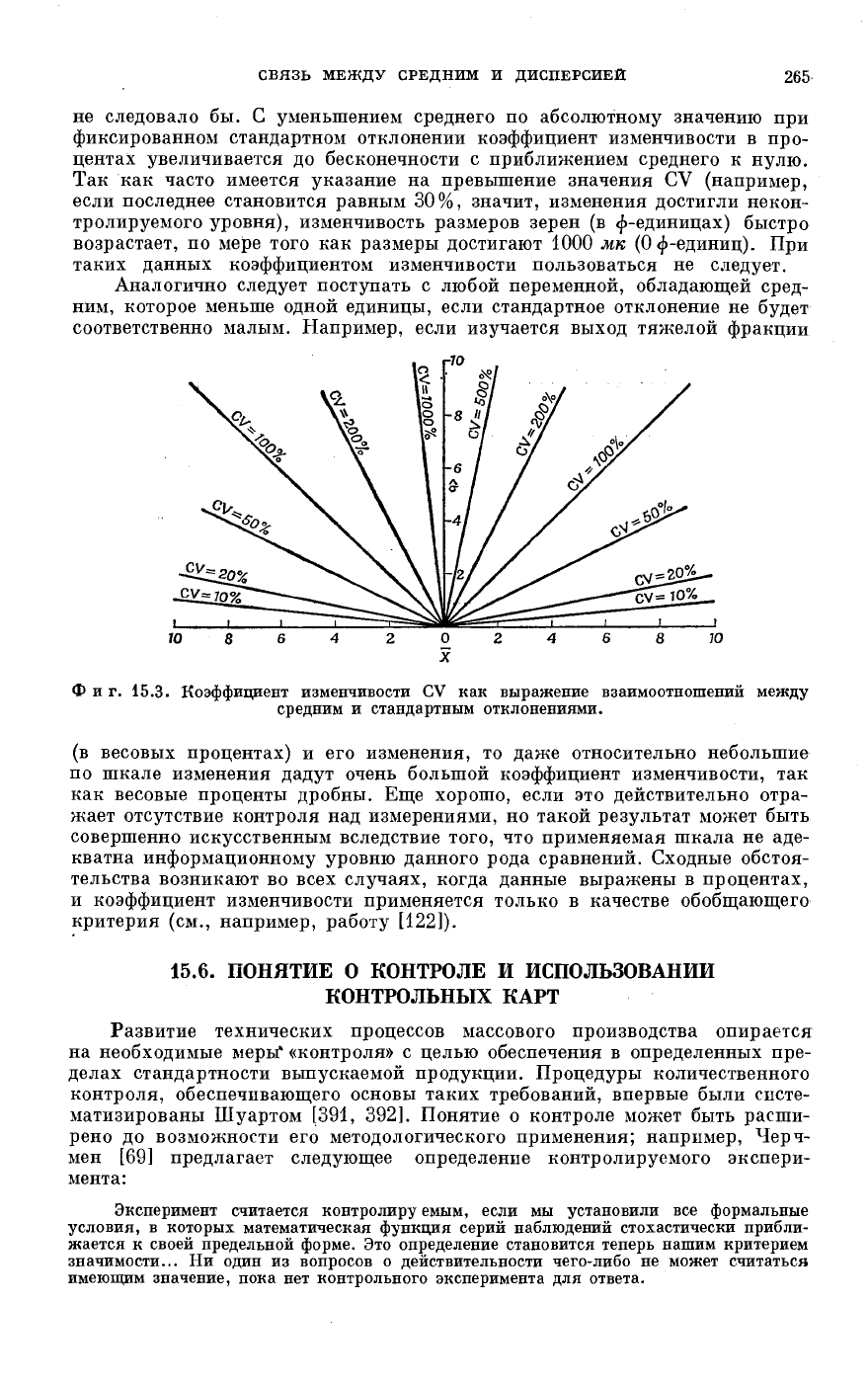
На фиг. 15.3 коэффициент изменчивости графически представлен как

зависимость стандартного отклонения от среднего. В этой диаграмме при-

меняется только ее правая часть; случайная переменная со значением

X = O имеет σ = 0 вследствие того, что нулевой пункт на шкале отклонений

обладает физическим смыслом. Но, чтобы достичь нормальности функции

распределения в случае, если переменная преобразована (например, в слу-

чае использования ф-преобразований для изучения размерности зерен),

допустимы отрицательные значения Xi и X, и на фиг. 15.3 эти данные могут

быть представлены в виде непрерывного интервала. График зависимости

между размерами и размерной отсортированностью на фиг. 15.2 является

тому примером, однако коэффициент изменчивости применять к этим данным

СВЯЗЬ МЕЖДУ СРЕДНИМ И ДИСПЕРСИЕЙ

265

не следовало бы. G уменьшением среднего по абсолютному значению при

фиксированном стандартном отклонении коэффициент изменчивости в про-

центах увеличивается до бесконечности с приближением среднего к нулю.

Так как часто имеется указание на превышение значения CV (например,

если последнее становится равным 30%, значит, изменения достигли некон-

тролируемого уровня), изменчивость размеров зерен (в ф-единицах) быстро

возрастает, по мере того как размеры достигают 1000 мк (0 ф-единиц). При

таких данных коэффициентом изменчивости пользоваться не следует.

Аналогично следует поступать с любой переменной, обладающей сред-

ним, которое меньше одной единицы, если стандартное отклонение не будет

соответственно малым. Например, если изучается выход тяжелой фракции

Фиг. 15.3. Коэффициент изменчивости CV как выражение взаимоотношений между

средним и стандартным отклонениями.

(в весовых процентах) и его изменения, то даже относительно небольшие

по шкале изменения дадут очень большой коэффициент изменчивости, так

как весовые проценты дробны. Еще хорошо, если это действительно отра-

жает отсутствие контроля над измерениями, но такой результат может быть

совершенно искусственным вследствие того, что применяемая шкала не аде-

кватна информационному уровню данного рода сравнений. Сходные обстоя-

тельства возникают во всех случаях, когда данные выражены в процентах,

и коэффициент изменчивости применяется только в качестве обобщающего

критерия (см., например, работу [122]).

15.6. ПОНЯТИЕ О КОНТРОЛЕ И ИСПОЛЬЗОВАНИИ

КОНТРОЛЬНЫХ КАРТ

Развитие технических процессов массового производства опирается

на необходимые Mepbf «контроля» с целью обеспечения в определенных пре-

делах стандартности выпускаемой продукции. Процедуры количественного

контроля, обеспечивающего основы таких требований, впервые были систе-

матизированы Шуартом [391, 392]. Понятие о контроле может быть расши-

рено до возможности его методологического применения; например, Черч-

мен [69] предлагает следующее определение контролируемого экспери-

мента:

Эксперимент считается контролиру емым, если мы установили все формальные

условия, в которых математическая функция серий наблюдений стохастически прибли-

жается к своей предельной форме. Это определение становится теперь нашим критерием

значимости... Ни один из вопросов о действительности чего-либо не может считаться

имеющим значение, пока нет контрольного эксперимента для ответа.

266

ГЛАВА 1 г

Здесь снова аналитические процедуры главным образом заключаются

в изучении связи среднего и дисперсии. Понятие же о контроле основано

на том, что при нормальном распределении вероятность некоторого события

в интервале X + ка может быть очень точно определена для любого выбран-

ного значения к, причем удобно использовать к = 2 или к = 3 с вероятно-

стями 95,4 и 99,7 соответственно. При контролируемых исследованиях,

однако, выборочные значения упорядочены, а относительно малые выборки

обычно усредняются и контрольные диаграммы применяются для изучения

изменений среднего путем использования контрольных границ X ± ка^

(где к = 2 или к = 3). В промышленности при количественном контроле

3<г

2 О-

2σ

3с

• · · · ,· ·

> · ·

• * · · ·

.·. .Ψ ·

Illtl

Приблизительно три значения на

IOOOO

находятся за пределами

3<г

2,5% значений

находятся

за преде-

лами

2СГ

95% значений

находятся

в пределах

этой площади

ZSJi значении за пределами Zcf

5 10 15 20

Порядок

наблюдений

за·

—X

* X

Х*"Х

XX X

* X "

1 1*1 I

1 5 Ю 15 19

Порядок наблюдений

Фиг. 15.4. Понятие о контроле.

А — контролируемые наблюдения; Б — неконтролируемые наблюдения.

наблюдения упорядочиваются по частоте появлений события, но эту про-

цедуру можно расширить до применения ее к любому основанию класси-

фикации, позволяющей производить рациональную группировку.

Предположим, что серия наблюдений упорядочена по частоте появления

событий; этот порядок определен на основе времени события или глубины,

на которой в скважине взят соответствующий образец (керн), или же по прин-

ципу географического положения на линии выбранного пересечения; тогда

изменения данной случайной величины подчиняются нормальному распре-

делению, среднее и стандартное отклонения могут быть оценены и наблю-

дения нанесены на контрольную карту, как это показано на фиг. 15.4, А.

Если наблюдения контролируемы, они будут случайно рассеяны вокруг

среднего значения, и лишь около 5 из 100 выйдут за пределы границ, нахо-

дящихся на расстоянии 2σ от среднего значения, или же можно ожидать, что

3 события из 1000 попадут за пределы границ, отстоящих на 3β от среднего.

Если значительное количество наблюдений перейдет эти границы, наблю-

дения следует считать неконтролируемыми. Можно полагать, что такие

наблюдения принадлежат другой совокупности, а не выбранной нами.

Однако упорядоченность наблюдений позволяет неаколько расширить

подобное обобщение; если наблюдения стали выходить за намеченные гра-

ницы, значит, применяемый до этого контроль недостаточен. Например,

идет выпуск некоторой промышленной продукции при контролируемом

процессе, и, если износ машин при этом происходит постепенно, серия

наблюдений покажет систематическое отклонение качества продукции.

Иными словами, характеристика случайных изменений будет потеряна.

Такие закономерности возникают при систематическом отклонении от нор-

СВЯЗЬ МЕЖДУ СРЕДНИМ И ДИСПЕРСИЕЙ

267

мы, и в этих случаях принято искать «определяющую причину» и удалять

источник изменчивости заменой изношенных частей в машине и т. п. Систе-

матическое отклонение от нормы может проявиться и в таком виде, как это

показано на фиг. 15.4, Б; подобный разрыв сети наблюдений служит преду-

преждением о неконтролируемости наблюдения.

Пример применения понятия о контроле с целью подразделения выбо-

рок описан Отто [316].

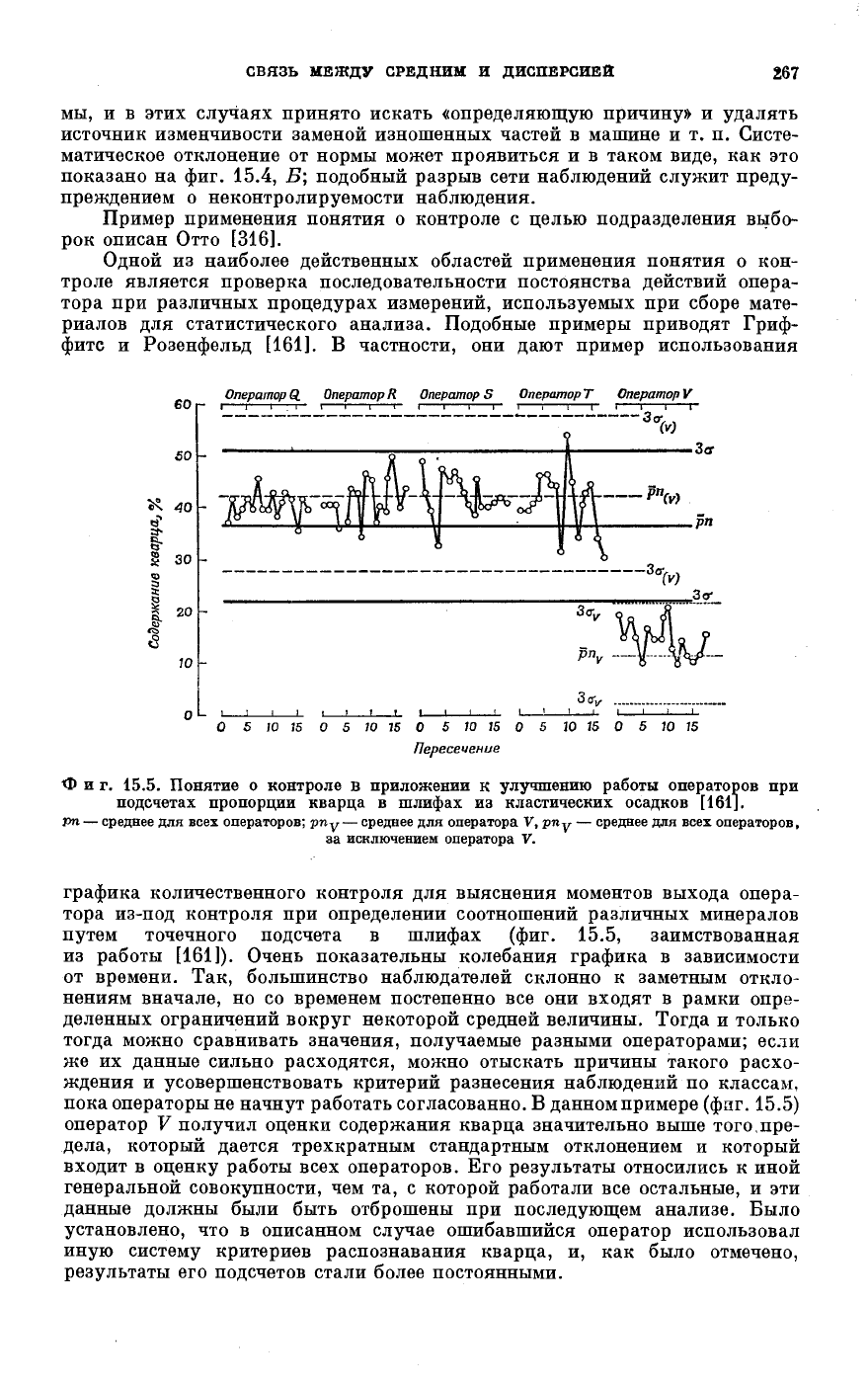
Одной из наиболее действенных областей применения понятия о кон-

троле является проверка последовательности постоянства действий опера-

тора при различных процедурах измерений, используемых при сборе мате-

риалов для статистического анализа. Подобные примеры приводят Гриф-

фите и Розенфельд [161]. В частности, они дают пример использования

Пересечение

Фиг. 15.5. Понятие о контроле в приложении к улучшению работы операторов при

подсчетах пропорции кварца в шлифах из пластических осадков [161].

Pn — среднее для всех операторов; ρηγ — среднее для оператора V, рпу — среднее для всех операторов,

за исключением оператора V.

графика количественного контроля для выяснения моментов выхода опера-

тора из-под контроля при определении соотношений различных минералов

путем точечного подсчета в шлифах (фиг. 15.5, заимствованная

из работы [161]). Очень показательны колебания графика в зависимости

от времени. Так, большинство наблюдателей склонно к заметным откло-

нениям вначале, но со временем постепенно все они входят в рамки опре-

деленных ограничений вокруг некоторой средней величины. Тогда и только

тогда можно сравнивать значения, получаемые разными операторами; если

же их данные сильно расходятся, можно отыскать причины такого расхо-

ждения и усовершенствовать критерий разнесения наблюдений по классам,

пока операторы не начнут работать согласованно. В данном примере (фиг. 15.5)

оператор V получил оценки содержания кварца значительно выше того, пре-

дела, который дается трехкратным стандартным отклонением и который

входит в оценку работы всех операторов. Его результаты относились к иной

генеральной совокупности, чем та, с которой работали все остальные, и эти

данные должны были быть отброшены при последующем анализе. Было

установлено, что в описанном случае ошибавшийся оператор использовал

иную систему критериев распознавания кварца, и, как было отмечено,

результаты его подсчетов стали более постоянными.

268

ГЛАВА 1 г

Однако не менее важные характеристики заметны на графиках других

операторов; например, оператор Q весьма постоянен в характере наблюде-

ний, кривая его данных мало меняется. Оператор S представляет более

нормальный случай; он начал с широкими отклонениями, а затем постепен-

но их сузил. Оператор R, вне сомнения, дал ухудшающиеся результаты,

отклонения его графика со временем увеличились; ясно, что в таком случае

необходимо изменить эту тенденцию. Аналогично действовал и опера-

тор Т, показавший необычно широкий размах отклонений; здесь также

необходимо было принять меры к улучшению положения. Все подобные

наблюдения представляют интерес, однако, судя по контрольному пределу

(обозначенному на фиг. 15.5 как Зо(у)), по показаниям операторов Q, R, S, T

(кроме оператора V) видно, что никакое из этих отклонений не выходит

за пределы 3σ; таким образом, упорядочивать наблюдения весьма необходимо

для того, чтобы можно было обнаружить недостаточность контроля. В гл. 19

и 20 будет отмечено, что любой оператор имеет склонность подсознательно

уменьшать чувствительность наблюдений, чем дает основание подразумевать

наличие взаимодействия между основными эффектами, что в определенном

случае может испортить весь эксперимент. Поэтому настойчиво рекомен-

дуется всякий раз, когда в исследовательской программе принимаются

новые методики или появляются новые операторы, применять метод кон-

трольных карт с целью возможности убедиться, что характеристика работы

контролируема.

ГЛАВА 16

Более общие критерии значимости.

Критерий Стьюдента

Несмотря на хорошо известное положение, согласно которому метод

использования нормальной кривой лишь тогда заслуживает доверия, когда

выборка «большая», до сих пор никто еще не сказал нам ясно, где граница

между «большим» и «малым».

Целью настоящей статьи является определение того момента, когда

можно использовать таблицы вероятностного интеграла для суждения

о значении средней величины из серии экспериментов и выбрать альтер-

нативные таблицы, когда слишком мало количество экспериментов.

Student, The Probable Error of a Mean, in E. S. Pearson,

J. Wishart (eds.), Student's Collected Papers, Biom. Off., Univ.

Coll., London, 1908

16.1. ВВЕДЕНИЕ

До сих пор приготовления к статистическому анализу ограничивались

главным образом сокращением множества данных и представлений их неко-

торой одной функцией распределения. При этом главная цель состояла в под-

боре подходящей модели; после этого можно было использовать статистиче-

ские оценки значений неизвестных параметров модели. Таким путем обшир-

ный набор данных мог быть обобщен в виде немногих представительных

статических оценок. Затем проводилась проверка представительности, иначе

говоря, если выбранная модель признавалась подходящей, проверялась

представительность выборок, т. е. их случайность. Затем рассматривалась

применимость функции распределения для проверки гипотез и выяснялось,

какого рода заключения могут быть выведены из набора полученных данных,

•особенно касающиеся их средних и дисперсий, и как сравнивать значения

среднего и дисперсии, полученные по единичной выборке, с полученными

по двум или более выборкам.

16.2. «-КРИТЕРИИ СТЬЮДЕНТА ДЛЯ ПРОВЕРКИ ГИПОТЕЗЫ

РАВЕНСТВА СРЕДНЕГО ЗАДАННОЙ ВЕЛИЧИНЕ

Эта основная процедура уже рассматривалась, когда выдвигались

предположения о нормальности распределения в предположении, что сред-

нее совокупности μ и дисперсия σ

известны. В общем эта процедура заклю-

чается в получении оценки вероятности встретить некоторое значение слу-

чайной величины X

, попадающее в интервал X

+ dX

; эта вероятность

была определена как эквивалентная отношению площади, соответствующей

+ dX

ко всей площади под частотной кривой (см. раздел 13.3 и ниже).

Необходимость знать значения μ и σ

ограничена применением такой про-

верки к тем необычным случаям, когда модель известна полностью и (или)

имеется достаточно обширная выборка для получения хороших оценок

параметров. В более общем случае модель адекватно аппроксимирует полу-

ченную кривую распределения, и о значении μ можно высказать некоторые

правдоподобные предположения, но величина σ

должна быть оценена

270

ГЛАВА 1 г

по небольшому набору выборочных данных. В подобном случае использо-

вание преобразования t = (X — μ)/σ или t = (X — μ) У N/а невозможно·

и его необходимо заменять другим:

g-rtV3v

> (161>

Вывод такой формы t впервые дал Госсетт, который опубликовал свои

работы под широко известным псевдонимом «Стьюдент». Считается, что его

классической работой, где он вывел равенство 16.1 [322, 418], положено

начало развитию статистических процедур с использованием малых выборок.

Это f-распределение определим с помощью χ

Теорема 1. Если величина X распределена нормально со средним μ и дис-

персией σ

a t = (X — μ)/σ, то t нормально распределена со средним, равным нулю,

и единичной дисперсией. Тогда сумма квадратов η случайных выборочных значений t

обладает х

-распределением с числом степеней свободы ν [198].

При этих условиях величина

t = t\ytlyt\+...+t\ (16.2)

обладает числом степеней свободы v.

Теперь рассмотрим критерий

(Ζ-μ) УN

используемый для проверки гипотезы, согласно которой выборочное мно-

жество X

взято из нормальной совокупности с определенным средним зна-

чением. • _

Выборочные средние X и дисперсия σ вычисляются по случайной выбор-

ке объемом п, отобранной из нормальной генеральной совокупности, со сред-

ним μ и дисперсией σ

. Следует отметить два свойства t [13]:

1. t — отношение между нормальным отклонением от среднего и корнем квадратным

из несмещенной оценки его дисперсии;

2. г — отношение между квадратом случайной величины у = У η (χ — μ)/σ, кото-

рая нормально распределена с параметрами 0,1 и случайной величиной O

, которая

распределена как χ

/ν с числом степеней свободы ·ν.

Тогда ί

= "

(

*Γ

μ)2/σ3

(16.3)

/σ

И t = J^LiJiiEl-Ini

' о/у η '

или t = ^. (16.4)

Этот критерий распределен по закону Стьюдента с ν = η = 1.

Заметим, что σ

не входит в это выражение, и требуется только один

параметр μ. Следовательно, посредством этого критерия можно, подставив,

ожидаемое значение μ, определить, является ли набор Xi случайной выбор-

кой из нормальной совокупности с параметром μ и σ

, вычисленным соответ-

ствующим образом по данным наблюдений.

Предположим снова, что в результате некоторого эксперимента полу-

чены две серии данных, содержащих Ti

и п

наблюдений, по которым соот-

ветственно вычислены X

и S

, и X

и S

. Тогда эти средние можно сравнить,

а различия проверить с помощью оценок дисперсии. Различие в средних

БОЛЕЕ ОБЩИЕ КРИТЕРИИ ЗНАЧИМОСТИ. КРИТЕРИЙ СТЬЮДЕНТА 271

может быть выражено как

-μ) -(X

-μ) = X

-X

. _ (16.5)

Если выбрана подходящая несмещенная оценка дисперсии сг

, других

параметров для такого критерия не требуется. Для применения ί-критерия

Стьюдента необходимо, чтобы переменная была разделена на квадратный

корень из несмещенной оценки ее (переменной) дисперсии, т. е.

Χ-μ

При таком определении X

- — независимые случайные замеры из нор-

мальной совокупности со средним μ, а величина t распределена по закону

Стьюдента с ν = η — 1 степенями свободы. Это преобразование названо

стъюдентизацией статистики и широко применяется при проверке гипо-

тезы о равенстве средних.

Плотность распределения t может быть выражена так [430]:

Плотность вероятности = { j[v—2)/2]! ^

2ti

} —

ехр

^Т^) ' (16·

)

Здесь есть только две переменные: число степеней свободы ν и аргу-

мент t.

Такое распределение симметрично и приближается к нормальному

по мере возрастания ν до бесконечности. В общем эта кривая несколько

менее заострена и более растянута, чем эквивалентная нормальная кри-

вая [198]. Для вычисления площадей под этими частотными кривыми опуб-

ликованы таблицы; наиболее популярной из них следует считать таблицы

Фишера [127], на которые всегда ссылаются в различных руководствах [15,

128]. Значения t приведены в этой таблице в колонках, соответствующих

заданным вероятностным уровням, а строки — степеням свободы.

16.3. ПРИМЕРЫ ПРИМЕНЕНИЯ « РАСПРЕДЕЛЕНИЯ СТЬЮДЕНТА

Во всех случаях, когда надо применить ί-критерий Стьюдента, необхо-

димо получить несмещенную оценку σ

для дисперсии σ

, причем, определяя

степень соответствия выбранной процедуры требованиям исследования,

необходимо быть особенно внимательным; наилучшей несмещенной оцен-

кой для σ

, полученной по выборкам, является

»=1

где η — число наблюдений X

в выборке (вывод см. в разделе 16.9).

Предположим, что мы располагаем данными измерений размеров девяти

кварцевых зерен (их длинных осей) по методу Халбе [203], и что получено

X = 2,00ф, σ = 0,6φ η η = 9.

Требуется проверить гипотезу случайного отбора этой выборки из совокуп-

ности, где μ = 0. По формуле

„ (Χ-μ) Vi

высчитываем

(2-0) V9 _ 6

- O^