Грехов В.П., Зарицкий М.Н., Ключникова Г.А., Куприков А.В. Теория автоматического управления
Подождите немного. Документ загружается.


Государственный комитет Российской Федерации
по высшему образованию
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ
В.П.Грехов, М.Н. Зарицкий, Г.А.Ключникова, А.В.Куприков
ТЕОРИЯ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Учебное пособие
для студентов специальностей
18.04.00 — Электропривод и автоматизация промышленных
установок и технологических комплексов
Москва 2003
СОДЕРЖАНИЕ
Стр.
1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ 3
2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЗВЕНЬЕВ И СИСТЕМ
АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
5
2.1. Передаточные функции линейных звеньев и систем
автоматического управления
5
2.2. Передаточные функции соединения звеньев 8
2.3. Структурные схемы линейных САУ и их преобразование 12
3. ХАРАКТЕРИСТИКИ ЛИНЕЙНЫХ ЗВЕНЬЕВ И СИСТЕМ 14
3.1. Временные характеристики 14
3.2. Частотные характеристики 15
3.3. Передаточные функции типовых динамических звеньев 18
3.4. Временные характеристики типовых динамических звеньев 22
3.5. Частотные характеристики типовых динамических звеньев 25
3.6. Построение логарифмических частотных характеристик
последовательного соединения звеньев
30
4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ
32
4.1. Введение в теорию устойчивости линейных стационарных
САУ
33
4.2. Алгебраический критерий устойчивости Гурвица 37
4.3. Частотный критерий устойчивости Найквиста 40
4.4. Анализ устойчивости по логарифмическим частотным
характеристикам. Запасы устойчивости
43
4.5. Влияние структуры и добротности системы на устойчивость 45
5. СИНТЕЗ ЗАМКНУТЫХ СИСТЕМ РЕГУЛИРОВАНИЯ 49
5.1.Содержание технических требований 49
5.2. Общий порядок синтеза корректирующего устройства и вид
желаемой ЛАЧХ
50
5.3. Передаточные функции типовых замкнутых систем
регулирования
59
5.4. Пример синтеза системы регулирования 60
5.5. Техническая реализация корректирующего устройства 68
2
6. МНОГОКОНТУРНЫЕ СИСТЕМЫ РЕГУЛИРОВАНИЯ 69
6.1. Многоконтурные системы с подчиненным регулированием
координат
69
6.2. Принципы оптимизации в системах подчиненного
регулирования
70
6.3. Порядок синтеза контуров в системах с подчиненным
регулированием координат
75
6.4. Тиристорный преобразователь и ШИР-регуляторы как
динамические звенья
78
3
1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Предметом ТАУ является изучение процессов поддержания на требуемом уровне или
изменения во времени по заданному закону каких-либо величин в машинах, аппаратах или в
других технических устройствах, протекающих без непосредственного участия человека с
помощью специальных приспособленных для этой цели приборов - автоматических
регуляторов, а также изучение способов проектирования и расчета таких систем.
ТАУ базируется на трех принципах, являющихся базой для всей кибернетики.
1) Принцип независимости выводов и основных положений теории управления от
физической природы устройств и протекающих в них процессов.
Изучаются не сами устройства, а процедура преобразования сигнала этими устройствами,
выражаемая в самом простом случае связью между входной и выходной величинами. Это
означает, что необходимо получить математическую модель (уравнение), определяющую
свойства устройства в переходном (динамическом) и установившемся режимах.
Система автоматического управления обычно состоит из ряда устройств, т.е. может быть
представлена рядом звеньев, имеющих между собой связи.
Широко используется метод схематического изображения систем: на этих схемах звенья
изображаются прямоугольниками, а сигналы - связывающими их линиями.
2) Принцип передачи сигналов в математической модели устройства или системы
управления заключается в том, что в каждом звене имеет место одностороннее
распространение информации. Одностороннее распространение информации позволяет
прослеживать пути прохождения сигналов в системах, как показано на рис.1.1.
Рис.1.1. Схема распространения сигналов
Согласно этому принципу обратное распространение информации обусловлено только за
счет обратной связи, т.е. передачи информации с выхода звена на вход одного из предыдущих
звеньев.
4
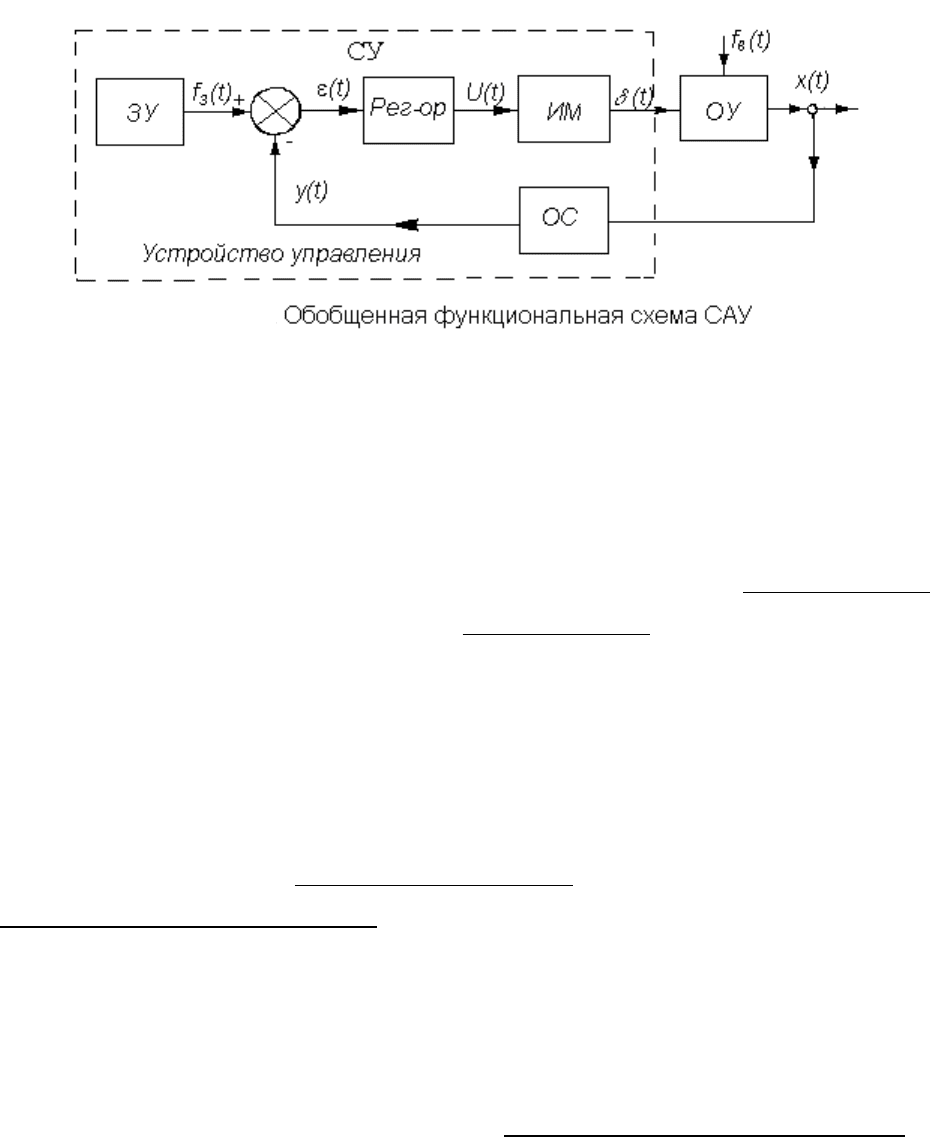
3) Принцип обратной связи состоит в том, что любая система автоматического
управления (САУ) имеет обратную связь, сигнал которой поступает с выхода на управляющий
вход.
В общем случае САУ, как показано на рис.1.2, состоит из объекта управления ОУ,
устройства обратной связи ОС, задающего устройства ЗУ, сравнивающего устройства СУ,
регулятора Рег и исполнительного механизма (ИМ).
Автоматическое управление возможно тогда, когда САУ построена таким образом, что
задающее воздействие fз(t) воспроизводится в регулируемую величину x(t) в соответствии с
требуемым алгоритмом функционирования. Для этого применяют обратную связь.
Воздействие выхода САУ на ее вход называют обратной связью. Введение обратной связи
позволяет управлять при действии на ОУ возмущающих воздействий fв(t). Возмущающие
воздействия могут быть внешними (например, сила или момент сопротивления) или
внутренними (они обусловлены изменениями параметров ОУ, например, из-за нагрева).
Комплекс устройств, присоединяемых к ОУ и обеспечивающих автоматическое
поддержание заданного значения его управляемой величины и изменение последней по
определенному закону, называют устройством управления (УУ).
Алгоритм функционирования УУ сводится к следующему: измерение фактического
значения управляемой величины, сравнение фактического значения с заданным, выработка
управляющего воздействия.
Таким образом, использование текущей информации об управляющих воздействиях и
переменных на выходе систем управления позволяет создать основной класс систем
управления - класс замкнутых систем управления с отрицательной обратной связью, в
которых можно обеспечить достижение заданных целей управления при большой
неопределенности возмущающих воздействий и изменения во времени параметров системы за
счет управления по отклонению управляемой величины от предписанного закона ее изменения.
5
Рис.1.2.

Управление - процесс организации такого целенаправленного воздействия на объект, в
результате которого объект переходит в требуемое (целевое) состояние. Более частным
случаем понятия “управление” является понятие “регулирование”. Регулирование состоит в
достижении такого функционирования системы, при котором выравниваются все отклонения
на выходе системы от заданного значения этого состояния, т.е. от нормы. Обеспечение только
требуемых значений параметров, определяющих желаемый ход технологического процесса в
том или ином объекте (например, металлорежущем станке) без участия человека,
осуществляется системой автоматического регулирования. Заданное значение или норма
состояния выхода системы может быть постоянной или переменной величиной.
Следовательно, регулирование есть выравнивание отклонений от нормы, каждое значение
которой определяется управлением.
2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЗВЕНЬЕВ И СИСТЕМ
АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Любые звенья и системы описываются дифференциальными уравнениями или
функциональными зависимостями (дифференциальными уравнениями нулевого порядка).
Уравнения системы включают всю совокупность звеньев системы.
Система называется линейной, если все ее звенья описываются линейными
дифференциальными уравнениями.
Если хотя бы одно из звеньев описывается нелинейным дифференциальным уравнением,
то это звено называется нелинейным и система тоже называется нелинейной. Это строгое
математическое определение. В практике ТАУ используется иное определение.
Если нелинейное дифференциальное уравнение звена удается заменить линейным
методом малых отклонений, то его называют линеаризуемым звеном.
При аналитических исследованиях система, содержащая только линейные или
линеаризуемые звенья, рассматривается как линейная. С точки зрения этого подхода к
нелинейным системам относят только системы, содержащие хотя бы одно существенно
нелинейное звено (существенную нелинейность), которое нельзя линеаризовать.
2.1. Передаточные функции линейных звеньев и систем автоматического управления
Каждая САУ состоит из ряда устройств, включая и объект управления. Для каждого
устройства (звена) получают математическую модель. Каждая переменная является функцией
времени. Возникает вопрос о том, каким образом использовать эти уравнения. Чтобы решить
этот вопрос, запишем линейное дифференциальное уравнение n-порядка:
6

)(
)(
...
)()(
)(
)(
...
)()(
01
1
1
1
01
1
1
1
tfb
dt
tdf
b
dt
tfd
b
dt
tfd
b
txa
dt
tdx
a
dt
txd
a
dt
txd
a
m
m
m
m
m
n
n
n
n
n
n
n
(2.1)
Любое движение линейного звена или системы представляет сумму свободного и
вынужденного движений
x(t) = x
св
(t) + x
вын
(t). (2.2)
x
св
(t) - это движение, возникающее при отсутствии входных воздействий (f(t)=0) и
зависящее от начальных условий.
x
вын
(t)- это движение, возникающее под влиянием входных воздействий из состояния
покоя (при нулевых начальных условиях).
Определим вынужденное движение линейной системы или линейного звена, используя
преобразование Лапласа.
Формула преобразования Лапласа
0
)()()( dtetfpFtfL
pt
(2.3)
Отметим, что функцию действительной переменной f(t) называют оригиналом, а
функцию комплексной переменной p F(p) называют изображением по Лапласу.
В соответствии с формулой (2.3) оригинал
)()(
1
pFLtf
.
Среди свойств преобразования Лапласа выделим свойство:
Если справедливо преобразование (2.3), то справедливо преобразование
n
k
kknn
n
n
fppFp
dt
tfd
L
1
)1(
)0()(
)(
. (2.4)
Запишем формулу (2.4) для случаев n=1 и n=2 (изображение по Лапласу для первой и
второй производных).
)0()(
)(
fppF
dt
tdf
L
,
)0()0()(
)(
2
2
2
ffppFp
dt
tdf
L
,
т.е. при ненулевых начальных условиях необходимо учитывать начальные условия оригинала и
(n-1) его производных.
При нулевых начальных условиях (рассматривается вынужденное движение)
nn
n
n
ppFpFp
dt
tfd
L )()(
)(
. (2.5)
7
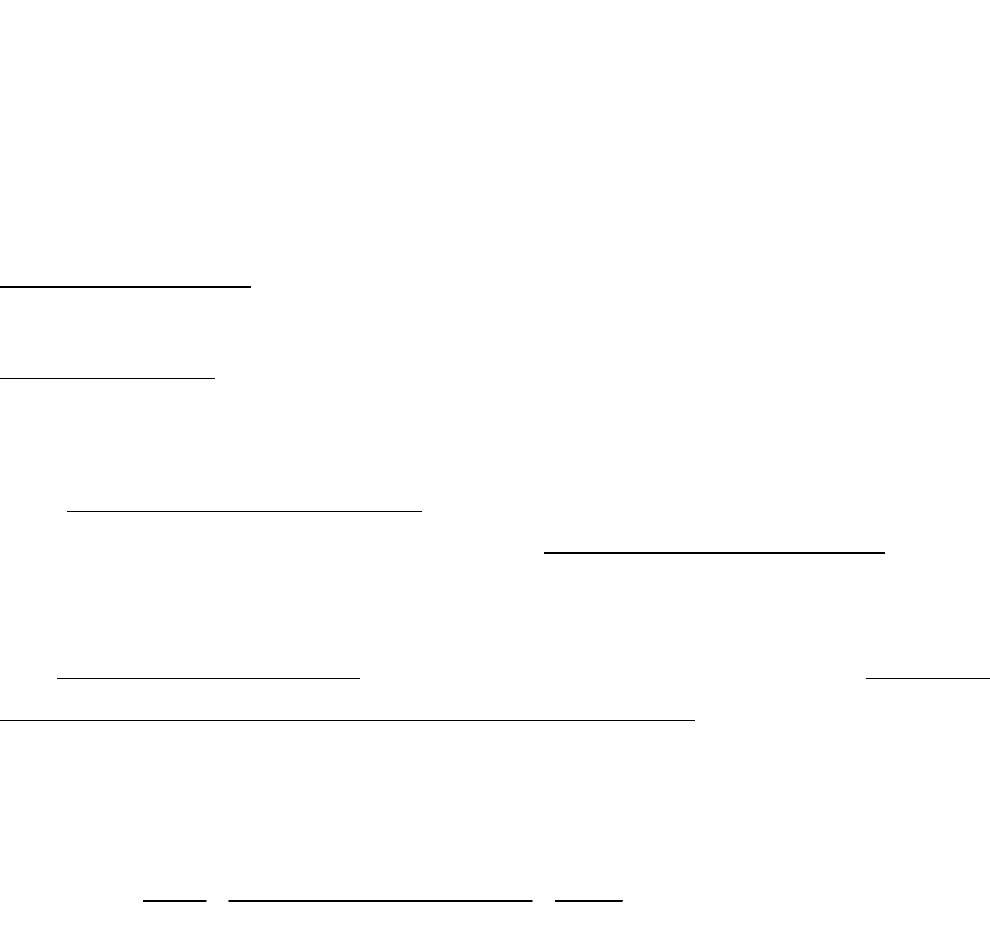
Выражение (2.5) показывает, что применение преобразования Лапласа к обеим частям
дифференциального уравнения позволяет “алгебраизировать” это уравнение, что упрощает
исследование линейных звеньев и систем.
Применив преобразование Лапласа при нулевых начальных условиях к обеим частям
дифференциального уравнения (2.1), получим уравнение в изображениях
)p(Fb)p(Fpb...)p(Fpb)p(Fpb
)p(Xa)p(Xpa...)p(Xpa)p(Xpa
01
1m
1m
m
m
01
1n
1n
n
n
, (2.6)
которое можно переписать в форме
)()()()( pFpMpXpD
, (2.7)
где
0
1
1
1
1
...)( apapapapD
n
n
n
n
- (2.8)
собственный оператор линейного звена или системы,
0
1
1
1
1
...)( bpbpbpbpM
m
m
m
m
- (2.9)
взаимный оператор линейного звена или системы.
Обратим внимание на то, что уравнение
0...)(
0
1
1
1
1
apapapapD
n
n
n
n
(2.10)
есть характеристическое уравнение линейного дифференциального уравнения (2.1).
Напомним, что корни этого уравнения определяют частоты свободных колебаний линейной
динамической системы или звена.
Взаимный оператор определяет преобразование входного воздействия.
Передаточной функцией линейного звена или системы называется отношение
изображений по Лапласу выходной и входной переменных (при нулевых начальных
условиях).
Из уравнений в изображениях (2.6) и (2.7) можно записать аналитическое выражение для
передаточной функции
)(
)(
...
...
)(
)(
)(
01
1
1
01
1
1
pD
pM
apapapa
bpbpbpb
pF
pX
pW
n
n
n
n
m
m
m
m
. (2.11)
Передаточная функция является важнейшей динамической характеристикой линейной
системы или звена, так как, зная передаточную функцию и изображение по Лапласу входного
сигнала, можно найти изображение по Лапласу выходной величины. Действительно, из (2.11)
следует, что
X(p) = W(p)·F(p). (2.12)
Напомним, что имеются таблицы соответствий оригиналов и их изображений по Лапласу.
Основные свойства передаточной функции:
8
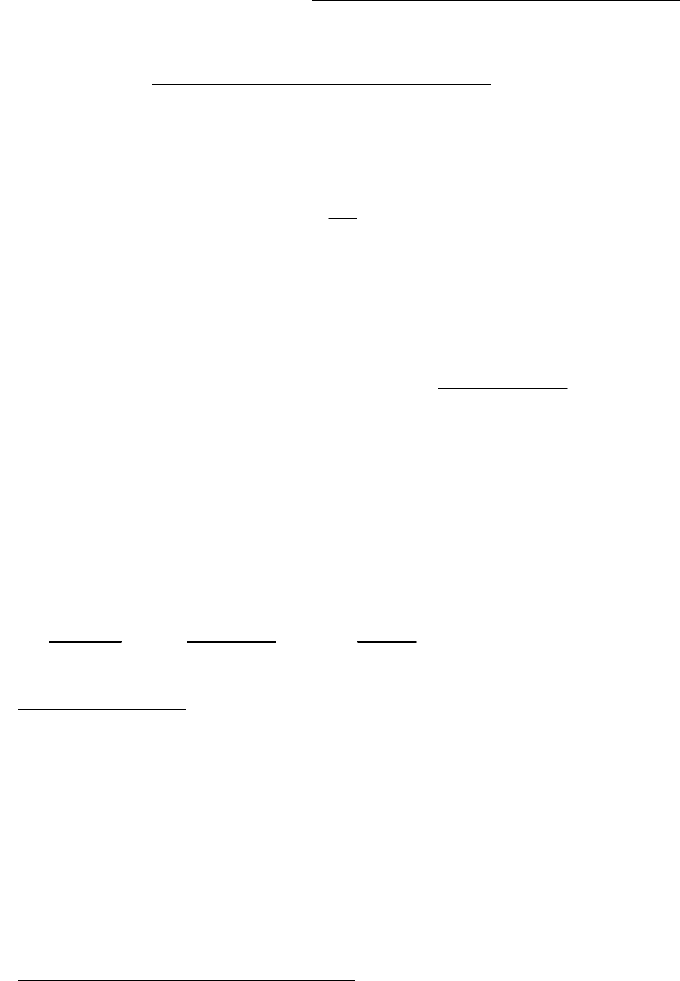
1) Во всякой физически реализуемой системе (звене) степень (m) полинома числителя
передаточной функции не больше степени (n) полинома ее знаменателя, т.е.
m
n . (2.13)
Это обусловлено тем, что в природе не существует идеальных дифференцирующих
устройств. Поэтому в реальных звеньях и системах реакция на выходе наступает после или в
момент приложения воздействия, т.е. при t
0.
2) Знаменатель передаточной функции D(p) - собственный оператор системы (звена) или
характеристический многочлен, а его нули есть корни характеристического уравнения (2.8). В
математике их принято называть полюсами передаточной функции, так как при комплексной
переменной p, равной любому полюсу, W(p) обращается в бесконечность. Корни уравнения
M(p)=0 называют нулями передаточной функции т.к. при комплексной переменной р, равной
любому нулю, числитель W(p) обращается в нуль.
3) При p=0 (см. (2.11))
0
0
)0(
b
a
W
=К (2.14)
есть передаточный коэффициент системы или звена.
Стандартная форма записи передаточной функции имеет вид
1...pE
1...pC
KpW
n
n
m
m
,
когда в полиномах числителя и знаменателя свободный член равен 1.
4) Свободное движение линейной системы или звена определяется полюсами
передаточной функции. Действительно, для нахождения свободного движения в
дифференциальном уравнении (2.1) следует положить f(t)=0. В результате получаем
0)(
)(
...
)()(
01
1
1
1
txa
dt
tdx
a
dt
txd
a
dt
txd
a
n
n
n
n
n
n
.
Общее решение этого однородного дифференциального уравнения имеет вид
tp
n
tptp
–‰
n
eCeCeCtx ...)(
21
21
, (2.15)
где
n
CCC ,...,.
21
- произвольные постоянные, определяемые начальными условиями,
n
ppp ,...,,
21
- корни характеристического уравнения (2.10).
2.2. Передаточные функции соединения звеньев
Последовательное соединение. Последовательным соединением звеньев называется
такое их соединение, при котором выходная величина предыдущего звена является входной
величиной последующего (рис. 2.1).
9

Необходимо найти W(p)=X(p)/F(p).
Из структурной схемы, показанной на рис. 2.1,
следуют очевидные соотношения:
U(p) = W
1
(p)·F(p), (2.16)
X(p) = W
2
(p)·U(p). (2.17)
Подставляя выражение (2.16) для U(p) в формулу (2.17), получим
X(p) = W
1
(p)· W
2
(p)·3F(p), 3 (2.18)
откуда следует, что
W(p) = X(p)/3F(p) = W
1
(p)· W
2
(p). (2.19)
Если последовательно соединены n звеньев, то по аналогии с (2.19) можно записать
n
i
i
pWpW
1
)()(
, (2.20)
где - знак произведения.
Таким образом, передаточная функция последовательного соединения звеньев равна
произведению передаточных функций звеньев, входящих в это соединение.
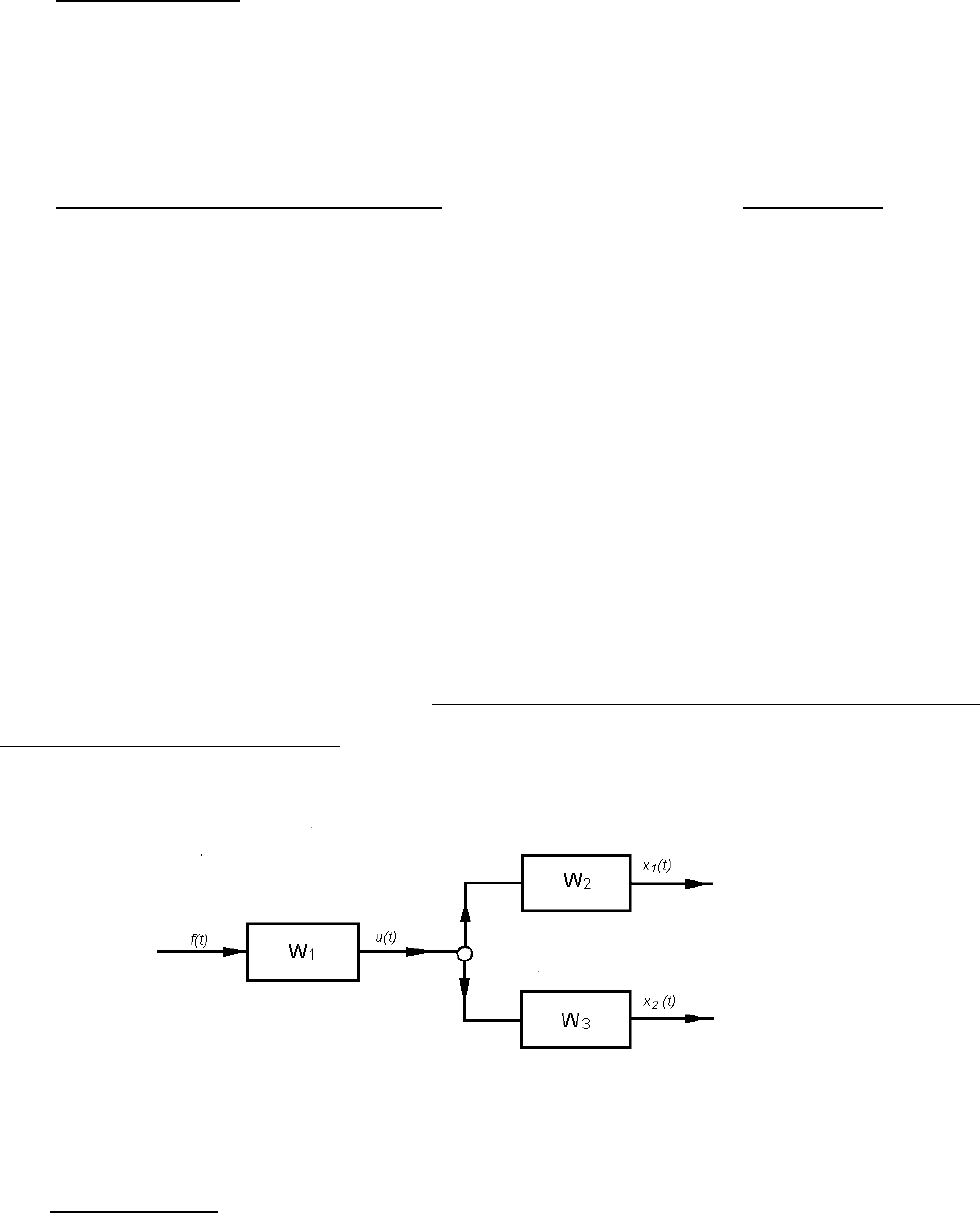
Параллельное соединение. Параллельным соединением звеньев называется такое их
соединение, при котором на входы всех таким образом соединенных звеньев подается одно и
то же воздействие, а выходные сигналы суммируются (рис.2.2). Необходимо найти W(p)=X(p)/
F(p).
Из структурной схемы, показанной на рис. 2.2, следуют очевидные соотношения:
X
1
(p)=W
1
(p)·F(p),
X
2
(p)=W
2
(p)·F(p).
X(p)=X
1
(p)+X
2
(p)=[W
1
(p)+ W
2
(p)]·F(p),
W(p)=X(p)/F(p)=W
1
(p)+ W
2
(p). (2.21)
Если параллельно соединены n звеньев, то по аналогии с (2.21) можно записать
10
Рис.2.2.
Рис.2.1.
