Грехов В.П., Зарицкий М.Н., Ключникова Г.А., Куприков А.В. Теория автоматического управления
Подождите немного. Документ загружается.


Продолжение табл. 3.1.
Тип звена
Характе-
ристика
Пропорциональное
(усилительное,
безынерционное)
Интегрирующее
Апериодическое
(инерционное)
Колебательное
Идеальное диф-
ференцирующее
звено
Запаздывающее
ЛАЧХ
L(
)
ФЧХ
(
)
29
3.6. Построение логарифмических частотных характеристик последовательного
соединения звеньев
Чтобы понять порядок построения ЛЧХ последовательного соединения звеньев,
рассмотрим два примера.
Пример 3.1.
)p(W)p(W)p(W)p(W
)1p4,0(р
)1p2(10
)p(W
4321
2
.
Это передаточная функция последовательного соединения безынерционного
усилительного звена W
1
(p)=10, двух интегрирующих звеньев W
2
(p)=
2
1
p
, апериодического
звена W
3
(p)=
14,0
1
p
и форсирующего звена с передаточной функцией W
4
(p)=2p+1.
Аналитическое выражение для ЛАЧХ этого соединения
L(
) = 20lg10 - 40lg
- 20lg
116,0
2
+ 20lg
14
2
.
Следует учесть, что строятся асимптотические ЛАЧХ. Построим их на рис. 3.15 и
графически просуммируем. При построении учтем сопрягающие частоты
сопр1
=1/2=0,5 с
-1
,
сопр2
=1/0,4=0,25 с
-1
и то, что ЛАЧХ двух интегрирующих звеньев (W
2
(p)=
2
1
p
) есть прямая с
наклоном -40 дБ/дек, пересекающая ось нуля децибел (ось частот) при
=1 с
-1
. Результатом
суммирования окажется ломаная линия, показанная на рис. 3.15.
Низкочастотная асимптота пройдет с наклоном -40 дБ/дек до сопрягающей частоты
сопр1
=0,5 с
-1
так, что ее продолжение будет зафиксировано в точке (
=1 с
-1
,
L
1
(
)=20lg10=20 дБ). На первой сопрягающей частоте наклон асимптоты изменится на +20
дБ по сравнению с наклоном предыдущей асимптоты и составит -20 дБ. На второй
сопрягающей частоте
сопр2
=0,25 с
-1
наклон асимптоты изменится на -20 дБ/дек по сравнению
с наклоном предыдущей асимптоты и составит -40 дБ/дек.
30

Рис. 3.15
Рассмотренное в примере 3.1 обоснование построения асимптотических ЛАЧХ
последовательного соединения типовых динамических звеньев можно свести к следующим
этапам:
1) По передаточной функции соединения звеньев находят 20lgK дБ и сопрягающие
частоты
сопр
i
=1/Т
i
.
2) Проводят низкочастотную асимптоту:
а) горизонтально, если отсутствуют интегрирующие и идеальные дифференцирующие
звенья (ордината этой горизонтали равна 20lgK дБ);
б) с наклоном -20
дБ/дек через точку с координатами (
=1 с
-1
, L(1)=20lgK дБ), если
имеется
интегрирующих звеньев;
в) с наклоном +20
дБ/дек через точку с координатами (
=1 с
-1
, L(1)=20lgK дБ), если
имеется
идеальных дифференцирующих звеньев.
3) На каждой сопрягающей частоте наклон асимптоты изменяется по отношению к
наклону предыдущей асимптоты на:
-20 дБ/дек - для апериодического звена,
-40 дБ/дек - для колебательного звена,
+20 дБ/дек - для форсирующего звена первого порядка W(p)=
1pT
ф
,
31

+40 дБ/дек - для форсирующего звена второго порядка
W
i
(p)33=
12
22
pTpT
ii
.
4) При необходимости производится уточнение асимптотической ЛАЧХ, что существенно
при наличии колебательных звеньев с относительными коэффициентами
<0,5.
ЛФЧХ последовательного соединения строится на основании алгебраического
суммирования ЛФЧХ звеньев, входящих в это соединение. В этом случае упростить
построение не удается.
При использовании ЭВМ производится точное построение ЛАЧХ и ЛФЧХ. При этом
необходимо задаться начальным и конечным значениями частоты и шагом ее изменения, при
котором обеспечивается необходимое число расчетных точек в пределах каждой декады.
В заключение отметим, что частотные характеристики позволяют судить о влиянии на
динамические свойства систем тех или иных звеньев и осуществлять анализ и синтез систем
автоматического управления. Поэтому ЛАЧХ и ЛФЧХ необходимо строить на одном
графике.
4. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ С ПОСТОЯННЫМИ ПАРАМЕТРАМИ
Одной из важнейших условий работоспособности САУ является устойчивость. Система,
не обладающая устойчивостью, вообще не способна выполнять функции управления.
Неустойчивая система может привести управляемый объект в аварийное состояние. Поэтому
проблема устойчивости САУ является одной из центральных в теории автоматического
управления.
Раскроем физический смысл понятия “устойчивость”. Устойчивость системы
автоматического управления и регулирования - это свойство системы возвращаться в
исходное состояние равновесия после прекращения воздействия, выведшего систему из
этого состояния.
Неустойчивая система не возвращается в исходное состояние, а непрерывно удаляется от
него.
Неустойчивость САУ возникает, как правило, из-за неправильного или очень сильного
действия главной обратной связи. Неправильное действие главной обратной связи имеет место
обычно в тех случаях, когда из-за ошибки, допущенной при монтаже системы связь
оказывается положительной (вместо отрицательной), что практически делает систему
неустойчивой. Возникающую при этом неустойчивость называют статической.
32

Более сложным и более распространенным видом неустойчивости является
динамическая неустойчивость. Она проявляется в системах с отрицательной обратной
связью при достаточно большом коэффициенте усиления (при порядке системы не меньшем
третьего). Причиной динамической неустойчивости обычно является значительная
инерционность элементов замкнутого контура, из-за которой в режиме колебаний системы
сигнал главной обратной связи значительно отстает от входного сигнала и оказывается с ним в
фазе. Это означает, что связь, выполненная конструктивно как отрицательная (в статическом
режиме!) в динамике (в режиме гармонических колебаний) проявляется на определенной
частоте как положительная.
4.1. Введение в теорию устойчивости линейных стационарных САУ
Рассмотрим математическую сущность устойчивости и неустойчивости линейных
стационарных САУ. Согласно данному выше физическому определению устойчивость зависит
только от характера свободного движения системы. Свободное движение линейной или
линеаризованной системы описывается однородным дифференциальным уравнением
0)(
)(
...
)()(
01
1
1
1
tXa
dt
tdx
a
dt
txd
a
dt
txd
a
n
n
n
n
n
n
,
(4.1)
где x(t) = x
св
(t) - свободная составляющая выходной величины системы.
Вынужденная составляющая выходной величины, зависящая от вида внешнего
воздействия и правой части дифференциального уравнения (2.1), на устойчивость системы не
влияет.
Математическое определение понятия “устойчивость”
Система является устойчивой, если свободная составляющая x
св
(t) переходного процесса
с течением времени стремится к нулю, т.е. если
0)(lim
tx
св
t
(4.2)
Очевидно, что при этом выходная величина системы будет стремиться к вынужденной
составляющей, определяемой правой частью уравнения (2.1). Устойчивость в смысле условия
(4.2) принято называть асимптотической.
Если свободная составляющая неограниченно взрастает, т.е. если
)(lim t
св
x
t
, (4.3)
то система неустойчива.
Наконец, если свободная составляющая не стремится ни к нулю, ни к бесконечности, то
система находится на границе устойчивости.
33
Найдем общее условие, при котором система, описываемая уравнением (4.1), устойчива.
Решение уравнения (4.1)
x
св
(t) =
n
k
tp
k
k
eC
1
, (4.4)
где C
k
- постоянные интегрирования, зависящие от начальных условий;
p
k
- корни характеристического уравнения
0...
01
1
1
apapapa
n
n
n
n
. (4.5)
Корни характеристического уравнения могут быть действительными (p
k
=
k
), мнимыми
(p
k
=j
k
) и комплексными
p
k
=
k
j
k
, (4.6)
причем как комплексные, так и мнимые корни попарно сопряжены.
Свободная составляющая (4.4) удовлетворяет условию устойчивости, если каждое
слагаемое вида
0
tp
k
k
eC
. Характер этой функции времени зависит от вида корня p
k
.
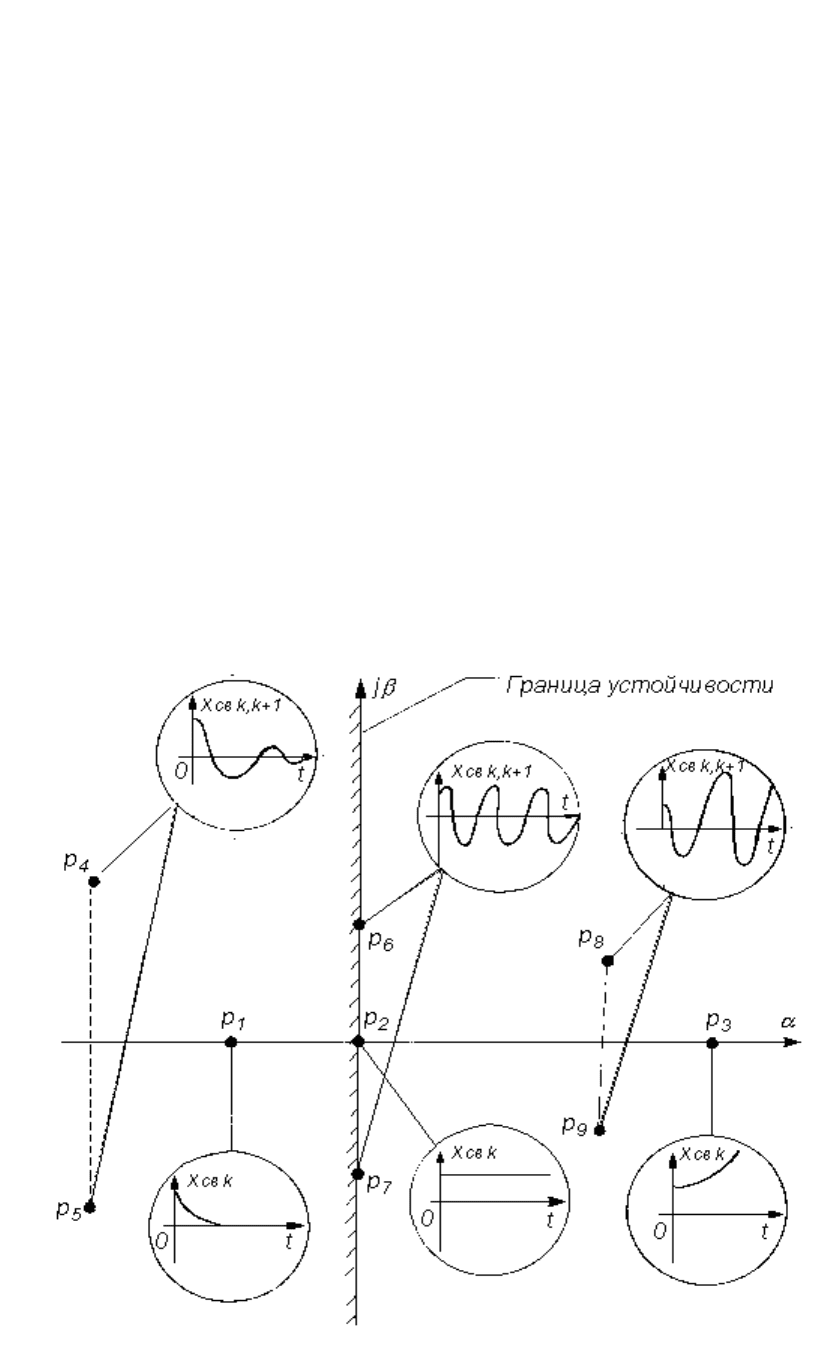
Рассмотрим все возможные случаи расположения корней характеристического уравнения
на комплексной плоскости (рис. 4.1) и соответствующие им функции x
св
(t), которые показаны
внутри кругов (как на экране осциллографа)
34

Рис. 4.1. Влияние корней характеристического уравнения на составляющие ее
свободного движения
1) Каждому действительному корню p
k
=
k
в решении (4.4) соответствует слагаемое вида
x
св
k
(t) =
tp
k
k
eC
. (4.7)
Если
k
<0 (корень p
1
), то функция (4.7) плавно стремится к нулю. Если
k
>0 (корень p
3
),
то функция (4.7) неограниченно возрастает. Если
k
=0 (корень p
2
), то эта функция остается
постоянной.
2) Каждой паре сопряженных комплексных корней p
k
=
k
+j
k
и p
k+1
=
k
-j
k
в решении
(4.4) соответствуют два слагаемых, которые могут быть объединены в одно слагаемое
x
св
k
(t) = 2
t
k
k
eC
sin(
k
t+
k
). (4.8)
Функция (4.8) представляет собой синусоиду с частотой
k
и амплитудой, изменяющейся
по экспоненте. Если
k
<0 (корни p
4
и p
5
на рис. 4.1), то колебательная составляющая (рис. 4.1)
будет затухать.
Если
k
>0 (корни p
8
и p
9
),то амплитуда колебаний будет неограниченно возрастать.
Наконец, если
k
=0 (корни p
6
и p
7
), т.е. оба сопряженных корня - мнимые (p
k
=j
k
, p
k+1
=-j
k
),
то x
св
k
(t)=2
tp
k
k
eC
sin(
k
t+
k
) - незатухающая синусоида
k
.
Если среди корней характеристического уравнения (4.5) имеются l равных между собой
корней p
l
, то в решении (4.4) вместо l слагаемых вида
C e
k
p t
k
появится одна составляющая
tp
l
l
l
etCtC„ )...(
1
110
. (4.9)
Учитывая, что функция вида
bt
e
при любом b убывает быстрее, чем возрастают слагаемые
вида
r
t
, можно доказать, что и в случае кратности корней решение (4.4) будет стремиться к
нулю лишь при отрицательности действительной части кратных корней p
l
.
На основании проведенного анализа можно сформулировать общее условие
устойчивости:
для устойчивости линейной стационарной САУ необходимо и достаточно, чтобы
действительные части всех корней характеристического уравнения системы были
отрицательными.
При этом действительные корни рассматриваются как частный случай комплексных
корней, у которых мнимая часть равна нулю. Если хотя бы один корень имеет положительную
действительную часть, то система будет неустойчивой.
35
Устойчивость системы зависит только от вида корней характеристического уравнения и
не зависит от характера внешних воздействий на систему. Устойчивость есть внутреннее
свойство системы, присущее ей вне зависимости от внешних условий.
Используя геометрическое представление корней (4.6) на комплексной плоскости (см.
рис. 4.1) в виде векторов или точек, можно дать вторую формулировку общего условия
устойчивости (эквивалентную основной):
для устойчивости линейной стационарной САУ необходимо и достаточно, чтобы все
корни характеристического уравнения находились в левой полуплоскости.
Если хотя бы один корень находится в правой полуплоскости, то система будет
неустойчивой.
Мнимая ось j
(рис. 4.1) является границей устойчивости в плоскости корней. Если
характеристическое уравнение имеет одну пару мнимых корней (p
k
=j
k
, p
k+1
=-j
k
), то в
системе устанавливаются незатухающие гармонические колебания с круговой частотой
=
k
. В этом случае система находится на колебательной границе устойчивости.
Точка
= 0 на мнимой оси соответствует так называемому нулевому корню. Если
характеристическое уравнение имеет один нулевой корень, то система находится на
апериодической границе устойчивости. Если таких корня два, то система неустойчива (два
последовательно соединенных интегрирующих звена создают сдвиг по фазе -180 при всех
значениях частот).
Таким образом, для суждения об устойчивости линейной стационарной САУ достаточно
определить знаки действительных частей корней характеристического уравнения. Но для этого
необходимо вычислять корни характеристического уравнения.
В ТАУ разработан ряд методов, с помощью которых можно судить о том, имеются ли
корни с положительной действительной частью, не находя числовые значения самих корней.
Эти методы называются критериями устойчивости.
Простейшим критерием устойчивости является условие положительности
коэффициентов характеристического уравнения. Положительность коэффициентов
уравнения (4.4) является необходимым (но не достаточным!) условием устойчивости системы.
Это означает, что если все коэффициенты характеристического уравнения положительны, то
система может быть устойчивой и неустойчивой (при порядке системы n>2). Но если хотя бы
один коэффициент уравнения отрицателен или равен нулю, то система неустойчива.
Критерии устойчивости могут быть алгебраическими и частотными. Алгебраические
критерии устанавливают необходимые и достаточные условия отрицательности корней в
36

форме ограничений, накладываемых на определенные комбинации коэффициентов
характеристического уравнения.
Частотные критерии определяют связь между устойчивостью системы и формой ее
частотных характеристик.
4.2. Алгебраические критерии устойчивости
Наиболее распространен в инженерной практике алгебраический критерий Гурвица.
Ниже приведены формулировки и методика применения критерия Гурвица.
Критерий Гурвица.
Запишем характеристическое уравнение системы n-го порядка
0...
01
1
1
apapapa
n
n
n
n
.
Примечание. В некоторых учебниках и задачниках по курсу ТАУ используют другую
индексацию коэффициентов, а именно:
0...
1
1
10
nn
nn
apapapa
.
Однако, важна не индексация коэффициентов характеристического уравнения, а
соответствие каждого из них порядку производной в дифференциальном уравнении. Поэтому
формально целесообразно использовать форму записи, при которой индекс коэффициента
соответствует порядку производной.
Для анализа устойчивости с помощью критерия Гурвица необходимо составить матрицу
коэффициентов характеристического уравнения следующего вида:
01
4567
2345
123
1
.....
.......
.......
0..
0..
0..
0..00
aa
aaaa
aaaa
aaaa
aa
nnnn
nnnn
nnnn
nn
(4.10)
Линейная система устойчива, если при
a
n
> 0 положительны все диагональные миноры
матрицы коэффициентов, т.е.
1
=
1n
a
> 0
2
=
23
1
nn
nn
aa
aa
> 0
3
=
345
123
1
0
nnn
nnn
nn
aaa
aaa
aa
> 0
37

и т.д., или в общем виде
i
=
inininin
nnn
nnn
nn
aaaa
aaa
aaa
aa
...
.......
.......
.......
0...
0...
0...0
)32()22()12(
345
123
1
> 0, i = 1,2, ..., n (4.11)
Если хотя бы один из определителей (4.11) отрицателен, то система неустойчива.
Так как последний столбец главного определителя
n
содержит всегда только один
элемент
a
0
, отличный от нуля, то согласно известному свойству определителей
n
=
0
a
1n
. (4.12)
Если
n
= 0, а все остальные определители положительны, то система находится на
границе устойчивости. С учетом (4.12) это условие распадается на два:
0
a
= 0 и
1n
= 0. (4.13)
Условию
a
0
= 0 соответствует один нулевой корень, т.е. апериодическая граница
устойчивости, а условию
1n
= 0 - пара мнимых корней, т.е. колебательная граница
устойчивости.
Совершенно очевидно, что для систем первого и второго порядка необходимым и
достаточным условием устойчивости является положительность коэффициентов
характеристического уравнения.
Для системы третьего порядка с характеристическим уравнением
0
01
2
2
3
3
apapapa
условие устойчивости
0a,0aaaa
aa
aa
0, >a= 0,=a
2030312
10
32
2
113
(4.14)
Последнее неравенство при
a
0
>0 эквивалентно неравенству
2
>0. Следовательно, для
системы третьего порядка, кроме положительности всех коэффициентов характеристического
уравнения, требуется, чтобы
2
> 0.
Учитывая выражение для
2
, можно сформулировать мнемоническое правило оценки
устойчивости систем третьего порядка:
произведение средних коэффициентов характеристического уравнения должно быть
больше произведения крайних.
38
