Gregersen E. (editor) The Britannica Guide to Statistics and Probability
Подождите немного. Документ загружается.


7 The Britannica Guide to Statistics and Probability 7
60
Rewriting equation (4) as P ( A ∩ B ) = P ( A ) P ( B | A ) and
adding to this expression the same expression with A
replaced by A
c
(“not A ”) leads via equation (1) to the
equality
More generally, if A
1
, A
2
, . . . , A
n
are mutually exclusive
events and their union is the entire sample space, so that
exactly one of the A
k
must occur, essentially the same
argument gives a fundamental relation, which is frequently
called the law of total probability:
Applications of Conditional Probability
An application of the law of total probability to a prob-
lem originally posed by Christiaan Huygens is to fi nd
the probability of “gambler’s ruin.” Suppose two play-
ers, often called Peter and Paul, initially have x and m − x
dollars, respectively. A ball, which is red with probabil-
ity p and black with probability q = 1 − p , is drawn from
an urn. If a red ball is drawn, then Paul must pay Peter
one dollar, while Peter must pay Paul one dollar if the
ball drawn is black. The ball is replaced, and the game
continues until one player is ruined. It is quite diffi cult
to determine the probability of Peter’s ruin by a direct
analysis of all possible cases. But let
Q
( x ) denote that
probability as a function of Peter’s initial fortune x and
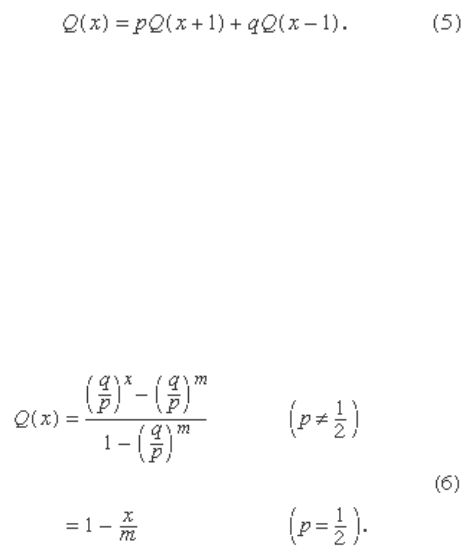
61
7
Probability Theory 7
observe that after one draw the structure of the rest of
the game is exactly as it was before the fi rst draw, except
that Peter’s fortune is now either x + 1 or x − 1 according
to the results of the fi rst draw. The law of total probabil-
ity with A = {red ball on fi rst draw} and A
c
= {black ball on
fi rst draw} shows that
This equation holds for x = 2, 3, . . . , m − 2. It also holds
for x = 1 and m − 1 if one adds the boundary conditions
Q
(0) = 1 and
Q
( m ) = 0, which say that if Peter initially has
0 dollars, his probability of ruin is 1, whereas if he has all m
dollars, he is certain to win.
It can be verifi ed by direct substitution that equation
(5) together with the indicated boundary conditions are
satisfi ed by
Additional analysis shows that these give the only solu-
tions and hence must be the desired probabilities.
Suppose m = 10 x , so that Paul initially has nine times as
much money as Peter. If p = 1/2, the probability of Peter’s
ruin is 0.9 regardless of the values of x and m . If p = 0.51, so
that each trial slightly favours Peter, then the situation is
quite different. For x = 1 and m = 10, the probability of
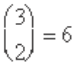
7 The Britannica Guide to Statistics and Probability 7
62
Peter’s ruin is 0.88, only slightly less than before. However,
for x = 100 and m = 1,000, Peter’s slight advantage on each
trial becomes so important that the probability of his ulti-
mate ruin is now less than 0.02.
Generalizations of the problem of gambler’s ruin play
an important role in statistical sequential analysis, devel-
oped by the Hungarian-born American statistician
Abraham Wald in response to the demand for more effi-
cient methods of industrial quality control during World
War II. They also enter into insurance risk theory.
The following example shows that, even when it is
given that A occurs, it is important in evaluating P(B|A) to
recognize that A
c
might have occurred, and hence in prin-
ciple it must be possible also to evaluate P(B|A
c
). By lot,
two out of three prisoners—Sam, Jean, and Chris—are
chosen to be executed. There are
possible pairs of prisoners to be selected for execution, of
which two contain Sam, so the probability that Sam is
slated for execution is 2/3. Sam asks the guard which of the
others is to be executed. Because at least one must be, it
appears that the guard would give Sam no information by
answering. After hearing that Jean is to be executed, Sam
reasons that, because either he or Chris must be the other
one, the conditional probability that he will be executed is
1/2. Thus, it appears that the guard has given Sam some
information about his own fate. However, the experiment
is incompletely defined, because it is not specified how
the guard chooses whether to answer “Jean” or “Chris” in
case both are to be executed. If the guard answers “Jean”
with probability p, then the conditional probability of the
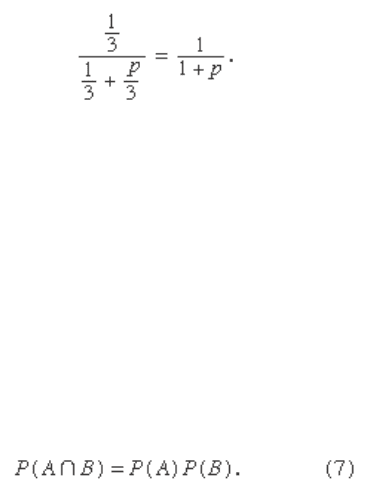
63
7
Probability Theory 7
event “Sam will be executed” given “the guard says Jean
will be executed” is
Only in the case p = 1 is Sam’s reasoning correct. If p = 1/2,
then the guard in fact gives no information about Sam’s fate.
Independence
One of the most important concepts in probability the-
ory is that of “independence.” The events A and B are
said to be (stochastically) independent if P ( B | A ) = P ( B ),
or equivalently if
The intuitive meaning of the defi nition in terms of condi-
tional probabilities is that the probability of B is not
changed by knowing that A has occurred. Equation (7)
shows that the defi nition is symmetric in A and B .
It is intuitively clear that, in drawing two balls with
replacement from an urn containing r red and b black
balls, the event “red ball on the fi rst draw” and the event
“red ball on the second draw” are independent. (This
statement presupposes that the balls are thoroughly mixed
before each draw.) An analysis of the ( r + b )
2
equally likely
outcomes of the experiment shows that the formal defi ni-
tion is indeed satisfi ed.
In terms of the concept of independence, the experi-
ment leading to the binomial distribution can be described
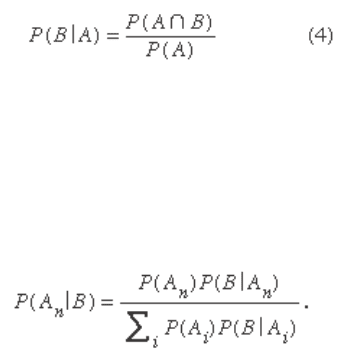
7 The Britannica Guide to Statistics and Probability 7
64
as follows. On a single trial, a particular event has proba-
bility p . An experiment consists of n independent
repetitions of this trial. The probability that the particular
event occurs exactly i times is given by equation (3).
Independence plays a central role in the law of large num-
bers, the central limit theorem, the Poisson distribution,
and Brownian motion.
Bayes’s Theorem
Consider now the defi ning relation for the conditional
probability P ( A
n
| B ), where the A
i
are mutually exclusive
and their union is the entire sample space. Substitution of
P ( A
n
) P ( B | A
n
) in the numerator of equation (4)
and substitution of the right-hand side of the law of total
probability in the denominator yields a result known as
Bayes’s theorem (after the 18th-century English clergy-
man Thomas Bayes) or the law of inverse probability:
As an example, suppose that two balls are drawn with-
out replacement from an urn containing r red and b black
balls. Let A be the event “red on the fi rst draw” and B the
event “red on the second draw.” From the obvious rela-
tions P ( A ) = r /( r + b ) = 1 − P ( A
c
), P ( B | A ) = (r − 1)/( r + b − 1),
P ( B | A
c
) = r /( r + b − 1), and Bayes’s theorem, it follows that

65
7
Probability Theory 7
the probability of a red ball on the first draw given that the
second one is known to be red equals (r − 1)/(r + b − 1). A
more interesting and important use of Bayes’s theorem
appears in the following text in the discussion of subjec-
tive probabilities.
RandoM vaRiables,
disTRibuTions, expecTaTion,
and vaRiance
Random Variables
Usually, it is more convenient to associate numerical
values with the outcomes of an experiment than to work
directly with a nonnumerical description such as “red
ball on the first draw.” For example, an outcome of the
experiment of drawing n balls with replacement from an
urn containing black and red balls is an n-tuple that tells
us whether a red or a black ball was drawn on each of the
draws. This n-tuple is conveniently represented by an
n-tuple of ones and zeros, where the appearance of a
one in the kth position indicates that a red ball was
drawn on the kth draw. A quantity of particular interest
is the number of red balls drawn, which is just the sum
of the entries in this numerical description of the exper-
imental outcome. Mathematically a rule that associates
with every element of a given set a unique real number
is called a “(real-valued) function.” In the history of sta-
tistics and probability, real-valued functions defined on
a sample space have traditionally been called “random
variables.” Thus, if a sample space S has the generic ele-
ment e, the outcome of an experiment, then a random
variable is a real-valued function X = X(e). Customarily
one omits the argument e in the notation for a random
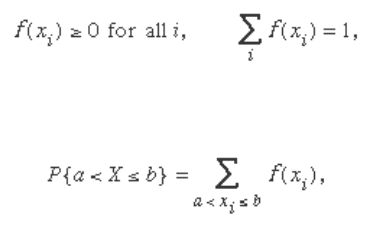
7 The Britannica Guide to Statistics and Probability 7
66
variable. For the experiment of drawing balls from an
urn containing black and red balls, R , the number of red
balls drawn, is a random variable. A particularly useful
random variable is 1[ A ], the indicator variable of the
event A , which equals 1 if A occurs and 0 otherwise.
A “constant” is a trivial random variable that always
takes the same value regardless of the outcome of the
experiment.
Probability Distribution
Suppose X is a random variable that can assume one of
the values x
1
, x
2
, . . . , x
m
, according to the outcome of
a random experiment, and consider the event { X = x
i
},
which is a shorthand notation for the set of all experi-
mental outcomes e such that X ( e ) = x
i
. The probability
of this event, P { X = x
i
}, is itself a function of x
i
, called the
probability distribution function of X . Thus, the distri-
bution of the random variable R defi ned in the preceding
section is the function of i = 0, 1, . . . , n given in the bino-
mial equation. Introducing the notation f ( x
i
) = P { X = x
i
},
one sees from the basic properties of probabilities that
and
for any real numbers a and b . If Y is a second random vari-
able defi ned on the same sample space as X and taking the
values y
1
, y
2
, . . . , y
n
, then the function of two variables

67
7
Probability Theory 7
h ( x
i
, y
j
) = P { X = x
i
, Y = y
j
} is called the joint distribution of X
and Y . Because { X = x
i
} = ∪
j
{ X = x
i
, Y = y
j
}, and this union
consists of disjoint events in the sample space,
Often f is called the marginal distribution of X to
emphasize its relation to the joint distribution of X and Y .
Similarly, g ( y
j
) = ∑
i
h ( x
i
, y
j
) is the (marginal) distribution of
Y . The random variables X and Y are defi ned to be inde-
pendent if the events { X = x
i
} and { Y = y
j
} are independent
for all i and j , such as if h ( x
i
, y
j
) = f ( x
i
) g ( y
j
) for all i and j . The
joint distribution of an arbitrary number of random vari-
ables is similarly defi ned.
Suppose two dice are thrown. Let X denote the sum
of the numbers appearing on the two dice, and let Y
denote the number of even numbers appearing. The pos-
sible values of X are 2, 3, . . . , 12, while the possible values
of Y are 0, 1, 2. Because there are 36 possible outcomes
for the two dice, the accompanying table giving the joint
JOINT DISTRIBUTION OF X AND Y
i
row
sum
= g(j)
j
2 3 4 5 6 7 8 9 10 11 12
0 1/36 0 1/18 0 1/12 0 1/18 0 1/36 0 0 1/4
1 0 1/18 0 1/9 0 1/6 0 1/9 0 1/18 0 1/2
2 0 0 1/36 0 1/18 0 1/12 0 1/18 0 1/36 1/4
column
sum =
f(i)
1/36 1/18 1/12 1/9 5/36 1/6 5/36 1/9 1/12 1/18 1/36
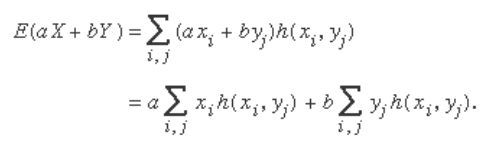
7 The Britannica Guide to Statistics and Probability 7
68
distribution h ( i , j ) ( i = 2, 3, . . . , 12; j = 0, 1, 2) and the mar-
ginal distributions f ( i ) and g ( j ) is easily computed by
direct enumeration.
For more complex experiments, determination of a
complete probability distribution usually requires a combi-
nation of theoretical analysis and empirical experimentation
and is often diffi cult. Consequently, it is desirable to
describe a distribution insofar as possible by a small num-
ber of parameters that are comparatively easy to evaluate
and interpret. The most important are the mean and the
variance. These are both defi ned in terms of the “expected
value” of a random variable.
Expected Value
Given a random variable X with distribution f , the expected
value of X , denoted E ( X ), is defi ned by E ( X ) = ∑
i
x
i
f ( x
i
).
In words, the expected value of X is the sum of each of
the possible values of X multiplied by the probability of
obtaining that value. The expected value of X is also called
the mean of the distribution f . The basic property of E is
that of linearity: If X and Y are random variables and if a
and b are both constants, then E ( a X + b Y ) = a E ( X ) + b E ( Y ).
To see why this is true, note that a X + b Y is itself a random
variable, which assumes the values a x
i
+ b y
j
with the prob-
abilities h ( x
i
, y
j
). Hence,
If the fi rst sum on the right-hand side is summed over
j while holding i fi xed, by equation (8)

69
7
Probability Theory 7
the result is
which by definition is E(X). Similarly, the second sum
equals E(Y).
If 1[A] denotes the “indicator variable” of A (i.e., a ran-
dom variable equal to 1 if A occurs and equal to 0
otherwise), then E{1[A]} = 1 × P(A) + 0 × P(A
c
) = P(A). This
shows that the concept of expectation includes that of
probability as a special case.
As an illustration, consider the number R of red balls
in n draws with replacement from an urn containing a pro-
portion p of red balls. From the definition and the binomial
distribution of R,
which can be evaluated by algebraic manipulation and
found to equal np. It is easier to use the representation
R = 1[A
1
] +⋯+ 1[An], where Ak denotes the event “the kth
draw results in a red ball.” Since E{1[Ak]} = p for all k, by
linearity E(R) = E{1[A
1
]} +⋯+ E{1[An]} = np. This argument
illustrates the principle that one can often compute the
expected value of a random variable without first comput-
ing its distribution. For another example, suppose n balls
are dropped at random into n boxes. The number of empty
boxes, Y, has the representation Y = 1[B
1
] +⋯+ 1[Bn], where
Bk is the event that “the kth box is empty.” Because the kth
box is empty if and only if each of the n balls went into one
