Gregersen E. (editor) The Britannica Guide to Statistics and Probability
Подождите немного. Документ загружается.


7 The Britannica Guide to Statistics and Probability 7
90
If a random variable X has a probability density func-
tion f ( x ), then its “expectation” can be defi ned by
provided that this integral is convergent. It turns out to be
simpler, however, not only to use Lebesgue’s theory of mea-
sure to defi ne probabilities but also to use his theory of
integration to defi ne expectation. Accordingly, for any ran-
dom variable X , E ( X ) is defi ned to be the Lebesgue integral
of X with respect to the probability measure P , provided
that the integral exists. In this way it is possible to provide
a unifi ed theory in which all random variables, both dis-
crete and continuous, can be treated simultaneously. To
follow this path, it is necessary to restrict the class of those
functions X defi ned on S that are to be called random vari-
ables, just as it was necessary to restrict the class of subsets
of S that are called events. The appropriate restriction is
that a random variable must be a measurable function. The
defi nition is taken over directly from the Lebesgue theory
of integration and will not be discussed here. It can be
shown that, whenever X has a probability density function,
its expectation (provided it exists) is given by equation (15),
which remains a useful formula for calculating E ( X ).
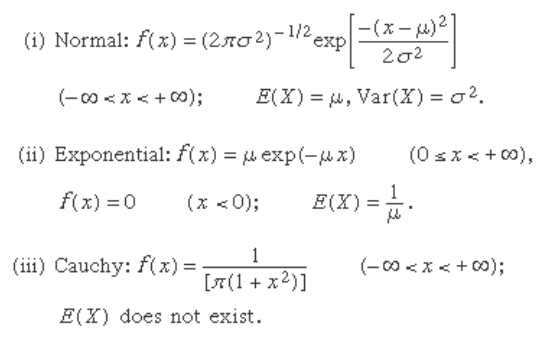
91
7
Probability Theory 7
Some important probability density functions are the
following:
The cumulative distribution function of the normal
distribution with mean 0 and variance 1 has already
appeared as the function G defi ned following equation
(12). The law of large numbers and the central limit theo-
rem continue to hold for random variables on infi nite
sample spaces. A useful interpretation of the central limit
theorem stated formally in equation (12) is as follows: The
probability that the average (or sum) of a large number of
independent, identically distributed random variables
with fi nite variance falls in an interval ( c
1
, c
2
] approximately
equals the area between c
1
and c
2
underneath the graph of a
normal density function chosen to have the same expecta-
tion and variance as the given average (or sum).
The exponential distribution arises naturally in the
study of the Poisson distribution introduced in equation
(13). If T
k
denotes the time interval between the emission
of the k − 1st and k th particle, then T
1
, T
2
, . . . are indepen-
dent random variables having an exponential distribution
with parameter μ. This is obvious for T
1
from the

7 The Britannica Guide to Statistics and Probability 7
92
observation that {T
1
> t} = {N(t) = 0}. Hence, P{T
1
≤ t} = 1 − P
{N(t) = 0} = 1 − exp(−μt), and by differentiation one obtains
the exponential density function.
The Cauchy distribution does not have a mean value
or a variance, because the integral (15) does not converge.
As a result, it has a number of unusual properties. For
example, if X
1
, X
2
, . . . , X
n
are independent random vari-
ables having a Cauchy distribution, then the average
(X
1
+⋯+ X
n
)/n also has a Cauchy distribution. The variabil-
ity of the average is exactly the same as that of a single
observation. Another random variable that does not have
an expectation is the waiting time until the number of
heads first equals the number of tails in tossing a fair coin.
condiTional expecTaTion
and leasT squaRes pRedicTion
An important problem of probability theory is to predict
the value of a future observation Y given knowledge of a
related observation X (or, more generally, given several
related observations X
1
, X
2
, . . .). Examples are to predict
the future course of the national economy or the path of a
rocket, given its present state.
Prediction is often just one aspect of a “control” prob-
lem. For example, in guiding a rocket, measurements of
the rocket’s location, velocity, and so on are made almost
continuously. At each reading, the rocket’s future course is
predicted, and a control is then used to correct its future
course. The same ideas are used to steer automatically
large tankers transporting crude oil, for which even slight
gains in efficiency result in large financial savings.
Given X, a predictor of Y is just a function H(X). The
problem of “least squares prediction” of Y given the obser-
vation X is to find that function H(X) that is closest to Y
in the sense that the mean square error of prediction,
93
7
Probability Theory 7
E{[Y − H(X)]
2
}, is minimized. The solution is the condi-
tional expectation H(X) = E(Y|X).
In applications a probability model is rarely known
exactly and must be constructed from a combination of
theoretical analysis and experimental data. It may be quite
difficult to determine the optimal predictor, E(Y|X), par-
ticularly if instead of a single X a large number of predictor
variables X
1
, X
2
, . . . are involved. An alternative is to restrict
the class of functions H over which one searches to mini-
mize the mean square error of prediction, in the hope of
finding an approximately optimal predictor that is much
easier to evaluate. The simplest possibility is to restrict
consideration to linear functions H(X) = a + bX. The coef-
ficients a and b that minimize the restricted mean square
prediction error E{(Y − a − bX)
2
} give the best linear least
squares predictor. Treating this restricted mean square
prediction error as a function of the two coefficients (a, b)
and minimizing it by methods of the calculus yield the
optimal coefficients: b
̂
= E{[X − E(X)][Y − E(Y)]}/Var(X)
and â = E(Y) − b
̂
E(X). The numerator of the expression
for b
̂
is called the covariance of X and Y and is denoted
Cov(X, Y). Let Ŷ = â + b
̂
X denote the optimal linear pre-
dictor. The mean square error of prediction is E{(Y − Ŷ)
2
} =
Var(Y) − [Cov(X, Y)]
2
/Var(X).
If X and Y are independent, Cov(X, Y) = 0, the optimal
predictor is just E(Y), and the mean square error of predic-
tion is Var(Y). Hence, |Cov(X, Y)| is a measure of the value
X has in predicting Y. In the extreme case that
[Cov(X, Y)]
2
= Var(X)Var(Y), Y is a linear function of X,
and the optimal linear predictor gives error-free
prediction.
In one important case the optimal mean square pre-
dictor actually is the same as the optimal linear predictor.
If X and Y are jointly normally distributed, then the con-
ditional expectation of Y given X is just a linear function

7 The Britannica Guide to Statistics and Probability 7
94
of X, and hence the optimal predictor and the optimal lin-
ear predictor are the same. The form of the bivariate
normal distribution as well as expressions for the coeffi-
cients â and b
̂
and for the minimum mean square error of
prediction were discovered by the English eugenicist Sir
Francis Galton in his studies of the transmission of inher-
itable characteristics from one generation to the next.
They form the foundation of the statistical technique of
linear regression.
The poisson pRocess and The
bRownian MoTion pRocess
The theory of stochastic processes attempts to build
probability models for phenomena that evolve over time.
A primitive example is the problem of gambler’s ruin.
The Poisson Process
An important stochastic process described implicitly in
the discussion of the Poisson approximation to the bino-
mial distribution is the Poisson process. Modeling the
emission of radioactive particles by an infinitely large num-
ber of tosses of a coin having infinitesimally small
probability for heads on each toss led to the conclusion
that the number of particles N(t) emitted in the time inter-
val [0, t] has the Poisson distribution given in equation (13)
with expectation μt. The primary concern of the theory of
stochastic processes is not this marginal distribution of
N(t) at a particular time but rather the evolution of N(t)
over time. Two properties of the Poisson process that make
it attractive to deal with theoretically are as follows: (i) The
times between emission of particles are independent and
exponentially distributed with expected value 1/μ; (ii) given
that N(t) = n, the times at which the n particles are emitted
95
7
Probability Theory 7
have the same joint distribution as n points distributed
independently and uniformly on the interval [0, t].
As a consequence of property (i), a picture of the func-
tion N(t) is easily constructed. Originally N(0) = 0. At an
exponentially distributed time T
1
, the function N(t) jumps
from 0 to 1. It remains at 1 another exponentially distrib-
uted random time, T
2
, which is independent of T
1
, and at
time T
1
+ T
2
it jumps from 1 to 2, and so on.
Examples of other phenomena for which the Poisson
process often serves as a mathematical model are the
number of customers arriving at a counter and requesting
service, the number of claims against an insurance com-
pany, or the number of malfunctions in a computer system.
The importance of the Poisson process consists in (a) its
simplicity as a test case for which the mathematical the-
ory, and hence the implications, are more easily understood
than for more realistic models and (b) its use as a building
block in models of complex systems.
Brownian Motion Process
The most important stochastic process is the Brownian
motion or Wiener process. It was first discussed by Louis
Bachelier (1900), who was interested in modeling fluc-
tuations in prices in financial markets, and by Albert
Einstein (1905), who gave a mathematical model for the
irregular motion of colloidal particles first observed by the
Scottish botanist Robert Brown in 1827. The first math-
ematically rigorous treatment of this model was given by
Wiener (1923). Einstein’s results led to an early, dramatic
confirmation of the molecular theory of matter in the
French physicist Jean Perrin’s experiments to determine
Avogadro’s number, for which Perrin was awarded a Nobel
Prize in 1926. Today somewhat different models for physi-
cal Brownian motion are deemed more appropriate than
96
7
The Britannica Guide to Statistics and Probability 7
Scottish botanist Robert Brown is best known for his description of the natu-
ral continuous motion of minute particles in solution, known as Brownian
movement. Hulton Archive/Getty Images

97
7
Probability Theory 7
Einstein’s, but the original mathematical model continues
to play a central role in the theory and application of sto-
chastic processes.
Let B ( t ) denote the displacement (in one dimension
for simplicity) of a colloidally suspended particle, which is
buffeted by the numerous much smaller molecules of the
medium in which it is suspended. This displacement will
be obtained as a limit of a random walk occurring in dis-
crete time as the number of steps becomes infi nitely large
and the size of each individual step infi nitesimally small.
Assume that at times k δ, k = 1, 2, . . . , the colloidal particle
is displaced a distance h X
k
, where X
1
, X
2
, . . . are +1 or −1
according as the outcomes of tossing a fair coin are heads
or tails. By time t the particle has taken m steps, where m
is the largest integer ≤ t /δ, and its displacement from its
original position is B
m
( t ) = h ( X
1
+⋯+ X
m
). The expected
value of B
m
( t ) is 0, and its variance is h
2
m , or approximately
h
2
t /δ. Now suppose that δ→ 0, and at the same time h → 0 in
such a way that the variance of B
m
(1) converges to some
positive constant, σ
2
. This means that m becomes infi nitely
large, and h is approximately σ( t / m )
1/2
. It follows from the
central limit theorem (equation [12])
that lim P { B
m
( t ) ≤ x } = G ( x /σ t
1/2
), where G ( x ) is the standard
normal cumulative distribution function defi ned just
below equation (12). The Brownian motion process B ( t )
can be defi ned to be the limit in a certain technical sense
of the B
m
( t ) as δ→ 0 and h → 0 with h
2
/δ → σ
2
.
The process B ( t ) has many other properties, which in
principle are all inherited from the approximating random
7 The Britannica Guide to Statistics and Probability 7
98
walk B
m
(t). For example, if (s
1
, t
1
) and (s
2
, t
2
) are disjoint
intervals, then the increments B(t
1
) − B(s
1
) and B(t
2
) − B(s
2
)
are independent random variables that are normally dis-
tributed with expectation 0 and variances equal to σ
2
(t
1
− s
1
)
and σ
2
(t
2
− s
2
), respectively.
Einstein took a different approach and derived various
properties of the process B(t) by showing that its probabil-
ity density function, g(x, t), satisfies the diffusion equation
∂g/∂t = D∂
2
g/∂x
2
, where D = σ
2
/2. The important implica-
tion of Einstein’s theory for subsequent experimental
research was that he identified the diffusion constant D in
terms of certain measurable properties of the particle (its
radius) and of the medium (its viscosity and temperature),
which allowed one to make predictions and hence to con-
firm or reject the hypothesized existence of the unseen
molecules that were assumed to be the cause of the irregu-
lar Brownian motion. Because of the beautiful blend of
mathematical and physical reasoning involved, a brief
summary of the successor to Einstein’s model is given in
the following text.
Unlike the Poisson process, it is impossible to “draw” a
picture of the path of a particle undergoing mathematical
Brownian motion. Wiener (1923) showed that the func-
tions B(t) are continuous, as one expects, but nowhere
differentiable. Thus, a particle undergoing mathematical
Brownian motion does not have a well-defined velocity,
and the curve y = B(t) does not have a well-defined tangent
at any value of t. To see why this might be so, recall that
the derivative of B(t), if it exists, is the limit as h → 0 of the
ratio [B(t + h) − B(t)]/h. Because B(t + h) − B(t) is normally
distributed with mean 0 and standard deviation h
1/2
σ, in
rough terms B(t + h) − B(t) can be expected to equal some
multiple (positive or negative) of h
1/2
. But the limit as h → 0
of h
1/2
/h = 1/h
1/2
is infinite. A related fact that illustrates
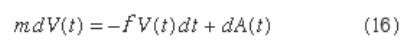
99
7
Probability Theory 7
the extreme irregularity of B(t) is that in every interval of
time, no matter how small, a particle undergoing math-
ematical Brownian motion travels an infinite distance.
Although these properties contradict the common sense
idea of a function—and indeed it is quite difficult to write
down explicitly a single example of a continuous, nowhere-
differentiable function—they turn out to be typical of a
large class of stochastic processes, called diffusion processes,
of which Brownian motion is the most prominent member.
Especially notable contributions to the mathematical the-
ory of Brownian motion and diffusion processes were made
by Paul Lévy and William Feller during the years 1930–60.
A more sophisticated description of physical Brownian
motion can be built on a simple application of Newton’s
second law: F = ma. Let V(t) denote the velocity of a col-
loidal particle of mass m. It is assumed that
The quantity f retarding the movement of the particle
is caused by friction resulting from the surrounding
medium. The term dA(t) is the contribution of the fre-
quent collisions of the particle with unseen molecules of
the medium. It is assumed that f can be determined by
classical fluid mechanics, in which the molecules making
up the surrounding medium are so many and so small that
the medium can be considered smooth and homogeneous.
Then by Stokes’s law, for a spherical particle in a gas,
f = 6πaη, where a is the radius of the particle and η the coef-
ficient of viscosity of the medium. Hypotheses concerning
A(t) are less specific, because the molecules making up the
surrounding medium cannot be observed directly. For
