Gregersen E. (editor) The Britannica Guide to Statistics and Probability

Подождите немного. Документ загружается.

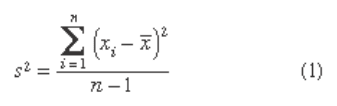
7 The Britannica Guide to Statistics and Probability 7

120

Percentiles provide an indication of how the data val-

ues are spread over the interval from the smallest value to

the largest value. Approximately p percent of the data val-

ues fall below the p th percentile, and roughly 100 − p

percent of the data values are above the p th percentile.

Percentiles are reported, for example, on most standard-

ized tests. Quartiles divide the data values into four parts;

the ﬁ rst quartile is the 25th percentile, the second quartile

is the 50th percentile (also the median), and the third

quartile is the 75th percentile.

The range, the difference between the largest value and

the smallest value, is the simplest measure of variability in

the data. The range is determined by only the two extreme

data values. The variance ( s

) and the standard deviation ( s ),

however, are measures of variability that are based on all

the data and are more commonly used. Equation 1 shows the

formula for computing the variance of a sample consisting

of n items. In applying equation 1, the deviation (difference)

of each data value from the sample mean is computed

and squared. The squared deviations are then summed and

divided by n − 1 to provide the sample variance.

The standard deviation is the square root of the vari-

ance. Because the unit of measure for the standard

deviation is the same as the unit of measure for the data,

many individuals prefer to use the standard deviation as

the descriptive measure of variability.

Outliers

Sometimes data for a variable will include one or more

values that appear unusually large or small and out of

121

Statistics 7

place when compared with the other data values. These

values are known as outliers and often have been errone-

ously included in the data set. Experienced statisticians

take steps to identify outliers and then review each one

carefully for accuracy and the appropriateness of its

inclusion in the data set. If an error has been made, then

corrective action, such as rejecting the data value in

question, can be taken. The mean and standard devia-

tion are used to identify outliers. A z-score can be

computed for each data value. With x representing the

data value, x¯ the sample mean, and s the sample stan-

dard deviation, the z-score is given by z = (x − x¯)/s. The

z-score represents the relative position of the data value

by indicating the number of standard deviations it is

from the mean. A rule of thumb is that any value with a

z-score less than −3 or greater than +3 should be consid-

ered an outlier.

Exploratory Data Analysis

Exploratory data analysis provides a variety of tools for

quickly summarizing and gaining insight about a set of

data. Two such methods are the ﬁve-number summary

and the box plot. A ﬁve-number summary simply consists

of the smallest data value, the ﬁrst quartile, the median,

the third quartile, and the largest data value. A box plot

is a graphical device based on a ﬁve-number summary. A

rectangle (i.e., the box) is drawn with the ends of the rect-

angle located at the ﬁrst and third quartiles. The rectangle

represents the middle 50 percent of the data. A verti-

cal line is drawn in the rectangle to locate the median.

Finally lines, called whiskers, extend from one end of the

rectangle to the smallest data value and from the other

end of the rectangle to the largest data value. If outliers

are present, then the whiskers generally extend only to

the smallest and largest data values that are not outliers.

7 The Britannica Guide to Statistics and Probability 7

122

Dots, or asterisks, are then placed outside the whiskers to

denote the presence of outliers.

pRobabiliTy

Probability is a subject that deals with uncertainty. In

everyday terminology, probability can be thought of as a

numerical measure of the likelihood that a particular

event will occur. Probability values are assigned on a scale

from 0 to 1, with values near 0 indicating that an event is

unlikely to occur and those near 1 indicating that an event

is likely to take place. A probability of 0.50 means that an

event is equally likely to occur as not to occur.

Based on a ﬁve-number summary, a box plot quickly summarizes and pro-

vides insight about a set of data. NIST/SEMATECH e-Handbook of

Statistical Methods (http://www.itl.nist.gov/div898/handbook/eda/

section3/boxplot.htm). Rendered by Rosen Educational Services

123

Statistics 7

Events and Their Probabilities

Oftentimes probabilities need to be computed for related

events. For instance, advertisements are developed for

the purpose of increasing sales of a product. If seeing the

advertisement increases the probability of a person buy-

ing the product, then the events “seeing the advertisement”

and “buying the product” are said to be dependent. If two

events are independent, then the occurrence of one event

does not affect the probability of the other event taking

place. When two or more events are independent, the

probability of their joint occurrence is the product of

their individual probabilities. Two events are said to be

mutually exclusive if the occurrence of one event means

that the other event cannot occur. In this case, when one

event takes place, the probability of the other event occur-

ring is zero.

Random Variables and

Probability Distributions

A random variable is a numerical description of the out-

come of a statistical experiment. A random variable that

may assume only a ﬁnite number or an inﬁnite sequence of

values is said to be discrete. One that may assume any

value in some interval on the real number line is said to be

continuous. For instance, a random variable representing

the number of automobiles sold at a particular dealership

on one day would be discrete, while a random variable rep-

resenting the weight of a person in kilograms (or pounds)

would be continuous.

The probability distribution for a random variable

describes how the probabilities are distributed over the

values of the random variable. For a discrete random

7 The Britannica Guide to Statistics and Probability 7

124

variable, x, the probability distribution is deﬁned by a

probability mass function, denoted by f(x). This function

provides the probability for each value of the random vari-

able. In the development of the probability function for a

discrete random variable, two conditions must be satis-

ﬁed: (1) f(x) must be nonnegative for each value of the

random variable, and (2) the sum of the probabilities for

each value of the random variable must equal one.

A continuous random variable may assume any value

in an interval on the real number line or in a collection of

intervals. Because there is an inﬁnite number of values in

any interval, it is not meaningful to talk about the proba-

bility that the random variable will take on a speciﬁc value.

Instead, the probability that a continuous random vari-

able will lie within a given interval is considered.

In the continuous case, the counterpart of the proba-

bility mass function is the probability density function,

also denoted by f(x). For a continuous random variable,

the probability density function provides the height or

value of the function at any particular value of x. It does

not directly give the probability of the random variable

taking on a speciﬁc value. However, the area under the

graph of f(x) corresponding to some interval, obtained by

computing the integral of f(x) over that interval, provides

the probability that the variable will take on a value within

that interval. A probability density function must satisfy

two requirements: (1) f(x) must be nonnegative for each

value of the random variable, and (2) the integral over all

values of the random variable must equal one.

The expected value, or mean, of a random variable—

denoted by E(x) or μ—is a weighted average of the

values the random variable may assume. In the discrete

case the weights are given by the probability mass func-

tion, and in the continuous case the weights are given by the

125

Statistics 7

probability density function. The formulas for computing

the expected values of discrete and continuous random

variables are given by equations (2) and (3), respectively.

E(x) = Σxf(x) (2)

E(x) = ∫xf(x)dx (3)

The variance of a random variable, denoted by Var(x)

or σ

, is a weighted average of the squared deviations

from the mean. In the discrete case the weights are given

by the probability mass function, and in the continu-

ous case the weights are given by the probability density

function. The formulas for computing the variances of

discrete and continuous random variables are given by

equations (4) and (5), respectively. The standard devia-

tion, denoted σ, is the positive square root of the variance.

Because the standard deviation is measured in the same

units as the random variable and the variance is measured

in squared units, the standard deviation is often the pre-

ferred measure.

Var(x) = σ

= Σ(x − μ)

f(x) (4)

Var(x) = σ

= ∫(x − μ)

f(x)dx (5)

Special Probability Distributions

The Binomial Distribution

Two of the most widely used discrete probability distribu-

tions are the binomial and Poisson. The binomial probability

mass function in equation (6) provides the probability that

x successes will occur in n trials of a binomial experiment.

7 The Britannica Guide to Statistics and Probability 7

126

A binomial experiment has four properties: (1) It con-

sists of a sequence of n identical trials; (2) two outcomes,

success or failure, are possible on each trial; (3) the proba-

bility of success on any trial, denoted p , does not change

from trial to trial; and (4) the trials are independent. For

example, suppose that it is known that 10 percent of the

owners of two-year old automobiles have had problems

with their automobile’s electrical system. To compute the

probability of ﬁ nding exactly 2 owners who have had elec-

trical system problems out of a group of 10 owners, the

binomial probability mass function can be used by setting

n = 10, x = 2, and p = 0.1 in equation (6). For this case the

probability is 0.1937.

The Poisson Distribution

The Poisson probability distribution is often used as a

model of the number of arrivals at a facility within a given

period of time. For instance, a random variable might be

deﬁ ned as the number of telephone calls coming into an

airline reservation system during a period of 15 minutes. If

the mean number of arrivals during a 15-minute interval is

known, then the Poisson probability mass function can be

used to compute the probability of x arrivals.

For example, suppose that the mean number of calls

arriving in a 15-minute period is 10. To compute the prob-

ability that 5 calls come in within the next 15 minutes, μ =

10 and x = 5 are substituted in equation (7), giving a proba-

bility of 0.0378.

127

Statistics 7

The Normal Distribution

The most widely used continuous probability distribution

in statistics is the normal probability distribution. Like all

normal distribution graphs, it is a bell-shaped curve.

Probabilities for the normal probability distribution can

be computed using statistical tables for the standard nor-

mal probability distribution, which is a normal probability

distribution with a mean of zero and a standard deviation

of one. A simple mathematical formula is used to convert

any value from a normal probability distribution with

mean μ and a standard deviation σ into a corresponding

value for a standard normal distribution. The tables for

the standard normal distribution are then used to com-

pute the appropriate probabilities.

There are many other discrete and continuous probabil-

ity distributions. Other widely used discrete distributions

include the geometric, the hypergeometric, and the

negative binomial. Other commonly used continuous dis-

tributions include the uniform, exponential, gamma,

chi-square, beta, t, and F.

esTiMaTion

It is often of interest to learn about the characteristics of

a large group of elements such as individuals, households,

buildings, products, parts, customers, and so on. All the ele-

ments of interest in a particular study form the population.

Because of time, cost, and other considerations, data often

cannot be collected from every element of the population.

In such cases, a subset of the population, called a sample, is

used to provide the data. Data from the sample are then

used to develop estimates of the characteristics of the larger

population. The process of using a sample to make infer-

ences about a population is called statistical inference.

7 The Britannica Guide to Statistics and Probability 7

128

Characteristics such as the population mean, the pop-

ulation variance, and the population proportion are called

parameters of the population. Characteristics of the

sample such as the sample mean, the sample variance, and

the sample proportion are called sample statistics. There

are two types of estimates: point and interval. A point esti-

mate is a value of a sample statistic that is used as a single

estimate of a population parameter. No statements are

made about the quality or precision of a point estimate.

Statisticians prefer interval estimates because interval

estimates are accompanied by a statement concerning the

degree of conﬁdence that the interval contains the popu-

lation parameter being estimated. Interval estimates of

population parameters are called conﬁdence intervals.

Sampling and Sampling Distributions

It should be noted here that the methods of statistical

inference, and estimation in particular, are based on the

notion that a probability sample has been taken. The key

characteristic of a probability sample is that each element

in the population has a known probability of being

included in the sample. The most fundamental type is a

simple random sample.

For a population of size N, a simple random sample is

a sample selected such that each possible sample of size n

has the same probability of being selected. Choosing the

elements from the population one at a time so that each

element has the same probability of being selected will

provide a simple random sample. Tables of random num-

bers, or computer-generated random numbers, can be

used to guarantee that each element has the same proba-

bility of being selected.

A sampling distribution is a probability distribution for

a sample statistic. Knowledge of the sampling distribution

129

Statistics 7

is necessary for the construction of an interval estimate

for a population parameter, which is why a probability

sample is needed. Without a probability sample, the sam-

pling distribution cannot be determined and an interval

estimate of a parameter cannot be constructed.

Estimation of a Population Mean

The most fundamental point and interval estimation pro-

cess involves the estimation of a population mean. Suppose

it is of interest to estimate the population mean, μ, for a

quantitative variable. Data collected from a simple ran-

dom sample can be used to compute the sample mean, x¯,

where the value of x¯ provides a point estimate of μ.

When the sample mean is used as a point estimate of

the population mean, some error can be expected owing

to the fact that a sample, or subset of the population, is

used to compute the point estimate. The absolute value of

the difference between the sample mean, x¯, and the pop-

ulation mean, μ, written |x¯ − μ|, is called the sampling error.

Interval estimation incorporates a probability statement

about the magnitude of the sampling error. The sampling

distribution of x¯ provides the basis for such a statement.

Statisticians have shown that the mean of the sam-

pling distribution of x¯ is equal to the population mean, μ,

and that the standard deviation is given by σ/√

n, where σ is

the population standard deviation. The standard devia-

tion of a sampling distribution is called the standard error.

For large sample sizes, the central limit theorem indicates

that the sampling distribution of x¯ can be approximated

by a normal probability distribution. As a matter of prac-

tice, statisticians usually consider samples of size 30 or

more to be large.

In the large-sample case, a 95% conﬁdence interval

estimate for the population mean is given by x¯ ± 1.96σ/√