Gregersen E. (editor) The Britannica Guide to Statistics and Probability

Подождите немного. Документ загружается.

7 The Britannica Guide to Statistics and Probability 7

100

example, it is assumed that for t ≠ s, the inﬁnitesimal ran-

dom increments dA(t) = A(t + dt) − A(t) and A(s + ds) − A(s)

caused by collisions of the particle with molecules of the

surrounding medium are independent random variables

having distributions with mean 0 and unknown variances

dt and σ

ds and that dA(t) is independent of dV(s) for s < t.

The differential equation (16)

has the solution

where β = f/m. From this equation and the assumed prop-

erties of A(t), it follows that E[V

(t)] → σ

/(2mf) as t → ∞.

Now assume that, in accordance with the principle of

equipartition of energy, the steady-state average kinetic

energy of the particle, m lim

t → ∞

E[V

(t)]/2, equals the aver-

age kinetic energy of the molecules of the medium.

According to the kinetic theory of an ideal gas, this is

RT/2N, where R is the ideal gas constant, T is the tem-

perature of the gas in kelvins, and N is Avogadro’s number,

the number of molecules in one gram molecular weight of

the gas. It follows that the unknown value of σ

can be

determined: σ

= 2RTf/N.

If one also assumes that the functions V(t) are con-

tinuous, which is certainly reasonable from physical

considerations, it follows by mathematical analysis that

A(t) is a Brownian motion process as previously deﬁned.

This conclusion poses questions about the meaning of the

initial equation (16), because for mathematical Brownian

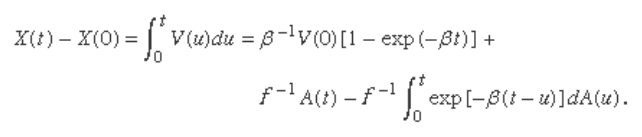
101

Probability Theory 7

motion the term d A ( t ) does not exist in the usual sense

of a derivative. Some additional mathematical analysis

shows that the stochastic differential equation (16) and its

solution equation (17) have a precise mathematical interpre-

tation. The process V ( t ) is called the Ornstein-Uhlenbeck

process, after the physicists Leonard Salomon Ornstein

and George Eugene Uhlenbeck. The logical outgrowth of

these attempts to differentiate and integrate with respect

to a Brownian motion process is the Ito (named for the

Japanese mathematician Itō Kiyosi) stochastic calculus,

which plays an important role in the modern theory of

stochastic processes.

The displacement at time t of the particle whose veloc-

ity is given by equation (17) is

For t large compared with β, the ﬁ rst and third terms

in this expression are small compared with the second.

Hence, X ( t ) − X (0) is approximately equal to A ( t )/ f , and

the mean square displacement, E {[ X ( t ) − X (0)]

}, is

approximately σ

/ f

= R T /(3π a η N ). These ﬁ nal conclusions

are consistent with Einstein’s model, but here they arise

as an approximation to the model obtained from equa-

tion (17). Because it is primarily the conclusions that

have observational consequences, there are essentially

no new experimental implications. However, the analysis

arising directly out of Newton’s second law, which yields

a process having a well-deﬁ ned velocity at each point,

seems more satisfactory theoretically than Einstein’s

original model.

7 The Britannica Guide to Statistics and Probability 7

102

sTochasTic pRocesses

A stochastic process is a family of random variables X ( t )

indexed by a parameter t , which usually takes values in the

discrete set Τ = {0, 1, 2, . . .} or the continuous set Τ = [0, +∞).

In many cases t represents time, and X ( t ) is a random vari-

able observed at time t . Examples are the Poisson process,

the Brownian motion process, and the Ornstein-

Uhlenbeck process described in the preceding section.

Considered as a totality, the family of random variables

{ X ( t ), t ∊ Τ} constitutes a “random function.”

Stationary Processes

The mathematical theory of stochastic processes attempts

to deﬁ ne classes of processes for which a uniﬁ ed theory can

be developed. The most important classes are stationary

processes and Markov processes. A stochastic process is

called stationary if, for all n , t

< t

<⋯< t

, and h > 0, then the

joint distribution of X ( t

+ h ), . . . , X ( t

+ h ) does not depend

on h . This means that in effect there is no origin on the time

axis. The stochastic behaviour of a stationary process is the

same no matter when the process is observed. A sequence of

independent identically distributed random variables is an

example of a stationary process. A rather different example

is deﬁ ned as follows: U (0) is uniformly distributed on [0, 1];

for each t = 1, 2, . . . , U ( t ) = 2 U ( t − 1) if U ( t − 1) ≤ 1/2, and

U ( t ) = 2 U ( t − 1) − 1 if U ( t − 1) > 1/2. The marginal distributions of

U ( t ), t = 0, 1, . . . are uniformly distributed on [0, 1], but, in

contrast to the case of independent identically distributed

random variables, the entire sequence can be predicted from

knowledge of U (0). A third example of a stationary process is

103

Probability Theory 7

where the Ys and Zs are independent normally distrib-

uted random variables with mean 0 and unit variance,

and the cs and θs are constants. Processes of this kind

can help model seasonal or approximately periodic

phenomena.

A remarkable generalization of the strong law of large

numbers is the ergodic theorem: If X(t), t = 0, 1, . . . for the

discrete case or 0 ≤ t < ∞ for the continuous case, is a sta-

tionary process such that E[X(0)] is ﬁnite, then with

probability 1 the average

if t is continuous, converges to a limit as s → ∞. In the spe-

cial case that t is discrete and the Xs are independent and

identically distributed, the strong law of large numbers is

also applicable and shows that the limit must equal E{X(0)}.

However, the example that X(0) is an arbitrary random

variable and X(t) =¯ X(0) for all t > 0 shows that this cannot

be true in general. The limit does equal E{X(0)} under an

additional rather technical assumption to the effect that

there is no subset of the state space, having probability

strictly between 0 and 1, in which the process can get

stuck and never escape. This assumption is not fulﬁlled by

the example X(t) =

X(0) for all t, which immediately gets

stuck at its initial value. It is satisﬁed by the sequence U(t)

previously deﬁned, so by the ergodic theorem the average

of these variables converges to 1/2 with probability 1. The

ergodic theorem was ﬁrst conjectured by the American

chemist J. Willard Gibbs in the early 1900s in the context

of statistical mechanics and was proved in a corrected,

abstract formulation by the American mathematician

George David Birkhoff in 1931.

7 The Britannica Guide to Statistics and Probability 7

104

Markovian Processes

A stochastic process is called Markovian (after the Russian

mathematician Andrey Andreyevich Markov) if at any

time t the conditional probability of an arbitrary future

event given the entire past of the process, i.e., given X(s)

for all s ≤ t, equals the conditional probability of that future

event given only X(t). Thus, to make a probabilistic state-

ment about the future behaviour of a Markov process, it is

no more helpful to know the entire history of the process

than it is to know only its current state. The conditional

distribution of X(t + h) given X(t) is called the transition

probability of the process. If this conditional distribution

does not depend on t, then the process is said to have “sta-

tionary” transition probabilities. A Markov process with

stationary transition probabilities may or may not be a

stationary process in the sense of the preceding paragraph.

If Y

, Y

, . . . are independent random variables and

X(t) = Y

+⋯+ Y

, then the stochastic process X(t) is a

Markov process. Given X(t) = x, the conditional probabil-

ity that X(t + h) belongs to an interval (a, b) is just the

probability that Y

t + 1

+⋯+ Y

t + h

belongs to the translated

interval (a − x, b − x). Because of independence this condi-

tional probability would be the same if the values of X(1), .

. . , X(t − 1) were also given. If the Ys are identically distrib-

uted as well as independent, this transition probability

does not depend on t, and then X(t) is a Markov process

with stationary transition probabilities. Sometimes X(t) is

called a random walk, but this terminology is not com-

pletely standard. Because both the Poisson process and

Brownian motion are created from random walks by sim-

ple limiting processes, they, too, are Markov processes

with stationary transition probabilities. The Ornstein-

Uhlenbeck process deﬁned as the solution (19) to the

105

Probability Theory 7

stochastic differential equation (18) is also a Markov pro-

cess with stationary transition probabilities.

The Ornstein-Uhlenbeck process and many other

Markov processes with stationary transition probabili-

ties behave like stationary processes as t → ∞. Generally, the

conditional distribution of X(t) given X(0) = x converges

as t → ∞ to a distribution, called the stationary distribu-

tion, that does not depend on the starting value X(0) = x.

Moreover, with probability 1, the proportion of time the

process spends in any subset of its state space converges

to the stationary probability of that set. If X(0) is given

the stationary distribution to begin with, then the process

becomes a stationary process. The Ornstein-Uhlenbeck

process deﬁned in equation (19) is stationary if V(0) has

a normal distribution with mean 0 and variance σ

/(2mf).

At another extreme are absorbing processes. An

example is the Markov process describing Peter’s fortune

during the game of gambler’s ruin. The process is absorbed

whenever either Peter or Paul is ruined. Questions of

interest involve the probability of being absorbed in one

state rather than another and the distribution of the time

until absorption occurs. Some additional examples of sto-

chastic processes follow.

The Ehrenfest Model of Diffusion

The Ehrenfest model of diffusion (named after the

Austrian Dutch physicist Paul Ehrenfest) was proposed in

the early 1900s to illuminate the statistical interpretation

of the second law of thermodynamics, that the entropy of

a closed system can only increase. Suppose N molecules of

a gas are in a rectangular container divided into two equal

parts by a permeable membrane. The state of the system

at time t is X(t), the number of molecules on the left-hand

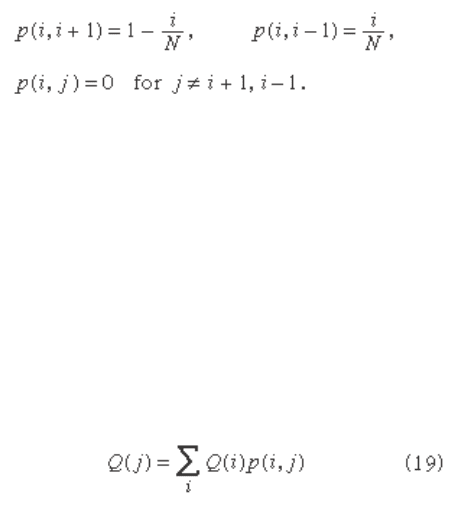
7 The Britannica Guide to Statistics and Probability 7

106

side of the membrane. At each time t = 1, 2, . . . a molecule

is chosen at random (i.e., each molecule has probability

1/ N to be chosen) and is moved from its present location

to the other side of the membrane. Hence, the system

evolves according to the transition probability p ( i , j ) =

P { X ( t + 1) = j | X ( t ) = i }, where

The long-run behaviour of the Ehrenfest process can

be inferred from general theorems about Markov pro-

cesses in discrete time with discrete state space and

stationary transition probabilities. Let T ( j ) denote the

ﬁ rst time t ≥ 1 such that X ( t ) = j and set T ( j ) = ∞ if X ( t ) ≠ j

for all t . Assume that for all states i and j it is possible for

the process to go from i to j in some number of steps, i.e.,

P { T ( j ) < ∞| X (0) = i } > 0. If the equations

have a solution

( j ) that is a probability distribution,

i.e.,

( j ) ≥ 0, and ∑

( j ) = 1, then that solution is unique

and is the stationary distribution of the process.

Moreover,

( j ) = 1/ E { T ( j )| X (0) = j }. For any initial state j ,

the proportion of time t that X ( t ) = i converges with

probability 1 to

( i ).

For the special case of the Ehrenfest process, assume

that N is large and X (0) = 0. According to the deterministic

prediction of the second law of thermodynamics, the

entropy of this system can only increase, which means that

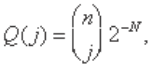
107

Probability Theory 7

X(t) will steadily increase until half the molecules are on

each side of the membrane. Indeed, according to the sto-

chastic model described earlier, there is overwhelming

probability that X(t) does increase initially. However,

because of random ﬂuctuations, the system occasionally

moves from conﬁgurations having large entropy to those of

smaller entropy and eventually even returns to its starting

state, in deﬁance of the second law of thermodynamics.

The accepted resolution of this contradiction is that

the length of time such a system must operate so an

observable decrease of entropy may occur is so enor-

mously long that a decrease could never be veriﬁed

experimentally. To consider only the most extreme case,

let T denote the ﬁrst time t ≥ 1 at which X(t) = 0 (i.e., the

time of ﬁrst return to the starting conﬁguration having all

molecules on the right-hand side of the membrane). It can

be veriﬁed by substitution in equation (18) that the sta-

tionary distribution of the Ehrenfest model is the binomial

distribution

and hence E(T) = 2

. For example, if N is only 100 and tran-

sitions occur at the rate of 10

per second, then E(T) is of

the order of 10

years. Hence, on the macroscopic scale,

on which experimental measurements can be made, the

second law of thermodynamics holds.

The Symmetric Random Walk

A Markov process that behaves in quite different and

surprising ways is the symmetric random walk. A particle

occupies a point with integer coordinates in d-dimensional

Euclidean space. At each time t = 1, 2, . . . it moves from its

7 The Britannica Guide to Statistics and Probability 7

108

present location to one of its 2d nearest neighbours with

equal probabilities 1/(2d), independently of its past moves.

For d = 1 this corresponds to moving a step to the right

or left according to the outcome of tossing a fair coin. It

may be shown that for d = 1 or 2 the particle returns with

probability 1 to its initial position and hence to every pos-

sible position inﬁnitely many times, if the random walk

continues indeﬁnitely. In three or more dimensions, at any

time t the number of possible steps that increase the dis-

tance of the particle from the origin is much larger than

the number decreasing the distance, with the result that the

particle eventually moves away from the origin and never

returns. Even in one or two dimensions, although the par-

ticle eventually returns to its initial position, the expected

waiting time until it returns is inﬁnite, there is no station-

ary distribution, and the proportion of time the particle

spends in any state converges to 0!

Queuing Models

The simplest service system is a single-server queue,

where customers arrive, wait their turn, are served by a

single server, and depart. Related stochastic processes are

the waiting time of the nth customer and the number of

customers in the queue at time t. For example, suppose

that customers arrive at times 0 = T

< T

< ⋯ and

wait in a queue until their turn. Let V

denote the service

time required by the nth customer, n = 0, 1, 2,…, and set

= T

− T

n − 1

. The waiting time, W

, of the nth customer

satisﬁes the relation W

= 0 and, for n ≥ 1, W

= max(0,

n − 1

+ V

n − 1

− U

). To see this, observe that the nth cus-

tomer must wait for the same length of time as the (n − 1)

th customer plus the service time of the (n − 1)th customer

minus the time between the arrival of the (n − 1)th and nth

customer, during which the (n − 1)th customer is already

109

Probability Theory 7

waiting but the nth customer is not. An exception occurs

if this quantity is negative, and then the waiting time of

the nth customer is 0. Various assumptions can be made

about the input and service mechanisms. One possibility

is that customers arrive according to a Poisson process

and their service times are independent, identically dis-

tributed random variables that are also independent

of the arrival process. Then, in terms of Y

= V

n − 1

− U

which are independent, identically distributed random

variables, the recursive relation deﬁning W

becomes

= max(0, W

n − 1

+ Y

). This process is a Markov process.

It is often called a random walk with reﬂecting barrier at

0, because it behaves like a random walk whenever it is

positive and is pushed up to be equal to 0 whenever it tries

to become negative. Quantities of interest are the mean

and variance of the waiting time of the nth customer and,

because these are difﬁcult to determine exactly, the mean

and variance of the stationary distribution. More realis-

tic queuing models try to accommodate systems with

In the single-server queue, as depicted by patients waiting for a vaccine,

customers arrive, wait their turn, are served by a single server, and depart.

Andrew Caballero-Reynolds/Getty Images