Gregersen E. (editor) The Britannica Guide to Statistics and Probability
Подождите немного. Документ загружается.


7 The Britannica Guide to Statistics and Probability 7
50
about relative frequencies of occurrence in a large number
of cases but are not predictions about a given individual.
expeRiMenTs, saMple space,
evenTs, and equally likely
pRobabiliTies
Applications of probability theory inevitably involve
simplifying assumptions that focus on some features of a
problem at the expense of others. Thus, it is advantageous
to begin by thinking about simple experiments, such as
tossing a coin or rolling dice, and to see how these appar-
ently frivolous investigations relate to important scientific
questions.
Applications of Simple
Probability Experiments
The fundamental ingredient of probability theory is an
experiment that can be repeated, at least hypothetically,
under essentially identical conditions and that may lead to
different outcomes on different trials. The set of all pos-
sible outcomes of an experiment is called a sample space.
The experiment of tossing a coin once results in a sample
space with two possible outcomes: heads and tails. Tossing
two dice has a sample space with 36 possible outcomes,
each of which can be identified with an ordered pair (i, j),
where i and j assume one of the values 1, 2, 3, 4, 5, 6 and
denote the faces showing on the individual dice. It is
important to think of the dice as identifiable (say by a dif-
ference in colour), so that the outcome (1, 2) is different
from (2, 1). An event is a well-defined subset of the sample
space. For example, the event “the sum of the faces show-
ing on the two dice equals six” consists of the five outcomes
(1, 5), (2, 4), (3, 3), (4, 2), and (5, 1).
51
7
Probability Theory 7
A third example is to draw n balls from an urn contain-
ing balls of various colours. A generic outcome to this
experiment is an n-tuple, where the ith entry specifies the
colour of the ball obtained on the ith draw (i = 1, 2,…, n). In
spite of the simplicity of this experiment, a thorough
understanding gives the theoretical basis for opinion polls
and sample surveys. For example, individuals in a popula-
tion favouring a particular candidate in an election may be
identified with balls of a particular colour, those favouring
a different candidate may be identified with a different
colour, and so on. Probability theory provides the basis for
learning about the contents of the urn from the sample of
balls drawn from the urn. An application is to learn about
the electoral preferences of a population on the basis of a
sample drawn from that population.
Another application of simple urn models is to use
clinical trials designed to determine whether a new treat-
ment for a disease, a new drug, or a new surgical procedure
is better than a standard treatment. In the simple case
in which treatment can be regarded as either success or
failure, the goal of the clinical trial is to discover whether
the new treatment more frequently leads to success than
does the standard treatment. Patients with the disease
can be identified with balls in an urn. The red balls are
those patients who are cured by the new treatment, and
the black balls are those not cured. Usually there is a con-
trol group, who receive the standard treatment. They are
represented by a second urn with a possibly different frac-
tion of red balls. The goal of the experiment of drawing
some number of balls from each urn is to discover on the
basis of the sample which urn has the larger fraction of
red balls. A variation of this idea can be used to test the
efficacy of a new vaccine. Perhaps the largest and most
famous example was the test of the Salk vaccine for polio-
myelitis conducted in 1954. It was organized by the U.S.
7 The Britannica Guide to Statistics and Probability 7
52
Public Health Service and involved almost two million
children. Its success has led to the almost complete elimi-
nation of polio as a health problem in the industrialized
parts of the world. Strictly speaking, these applications
are problems of statistics, for which the foundations are
provided by probability theory.
In contrast to the experiments previously described,
many experiments have infinitely many possible out-
comes. For example, one can toss a coin until heads
appears for the first time. The number of possible tosses
is n = 1, 2, . . . Another example is to twirl a spinner. For an
idealized spinner made from a straight line segment hav-
ing no width and pivoted at its centre, the set of possible
outcomes is the set of all angles that the final position of
the spinner makes with some fixed direction, equivalently
all real numbers in [0, 2π). Many measurements in the
natural and social sciences, such as volume, voltage, tem-
perature, reaction time, marginal income, and so on, are
made on continuous scales and at least in theory involve
infinitely many possible values. If the repeated measure-
ments on different subjects or at different times on the
same subject can lead to different outcomes, probability
theory is a possible tool to study this variability.
Because of their comparative simplicity, experiments
with finite sample spaces are discussed first. In the early
development of probability theory, mathematicians con-
sidered only those experiments for which it seemed
reasonable, based on considerations of symmetry, to sup-
pose that all outcomes of the experiment were “equally
likely.” Then in a large number of trials, all outcomes
should occur with approximately the same frequency. The
probability of an event is defined to be the ratio of the
number of cases favourable to the event (i.e., the number
of outcomes in the subset of the sample space defining the
event) to the total number of cases. Thus, the 36 possible
53
7
Probability Theory 7
outcomes in the throw of two dice are assumed equally
likely, and the probability of obtaining “six” is the number
of favourable cases, 5, divided by 36, or 5/36.
Now suppose that a coin is tossed n times, and con-
sider the probability of the event “heads does not occur”
in the n tosses. An outcome of the experiment is an n-tuple,
the kth entry of which identifies the result of the kth toss.
Because there are two possible outcomes for each toss,
the number of elements in the sample space is 2
n
. Of these,
only one outcome corresponds to having no heads, so the
required probability is 1/2
n
.
It is only slightly more difficult to determine the prob-
ability of “at most one head.” In addition to the single
case in which no head occurs, there are n cases in which
exactly one head occurs, because it can occur on the first,
second, . . . , or nth toss. Hence, there are n + 1 cases favour-
able to obtaining at most one head, and the desired
probability is (n + 1)/2
n
.
The Principle of Additivity
This last example illustrates the fundamental principle
that if the event whose probability is sought can be repre-
sented as the union of several other events that have no
outcomes in common (“at most one head” is the union of
“no heads” and “exactly one head”), then the probability of
the union is the sum of the probabilities of the individual
events making up the union. To describe this situation
symbolically, let S denote the sample space. For two events
A and B, the intersection of A and B is the set of all experi-
mental outcomes belonging to both A and B and is denoted
A ∩ B; the union of A and B is the set of all experimental
outcomes belonging to A or B (or both) and is denoted
A ∪ B. The impossible event (i.e., the event containing no
outcomes) is denoted by Ø. The probability of an event A
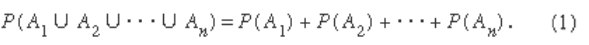
7 The Britannica Guide to Statistics and Probability 7
54
is written P ( A ). The principle of addition of probabilities
is that, if A
1
, A
2
, . . . , A
n
are events with A
i
∩ A
j
= Ø for all
pairs i ≠ j , then
Equation (1) is consistent with the relative frequency
interpretation of probabilities. For, if A
i
∩ A
j
= Ø for all
i ≠ j , the relative frequency with which at least one of the
A
i
occurs equals the sum of the relative frequencies with
which the individual A
i
occur.
Equation (1) is fundamental for everything that fol-
lows. Indeed, in the modern axiomatic theory of
probability, which eschews a defi nition of probability in
terms of “equally likely outcomes” as being hopelessly cir-
cular, an extended form of equation (1) plays a basic role.
An elementary, useful consequence of equation (1) is
the following. With each event A is associated the com-
plementary event A
c
consisting of those experimental
outcomes that do not belong to A . Because A ∩ A
c
= Ø,
A ∪ A
c
= S , and P ( S ) = 1 (where S denotes the sample
space), it follows from equation (1) that P ( A
c
) = 1 − P ( A ).
For example, the probability of “at least one head” in n
tosses of a coin is one minus the probability of “no head,”
or 1 − 1/2
n
.
Multinomial Probability
A basic problem fi rst solved by Jakob Bernoulli is to fi nd
the probability of obtaining exactly i red balls in the
experiment of drawing n times at random with replace-
ment from an urn containing b black and r red balls. To
draw at random means that, on a single draw, each of
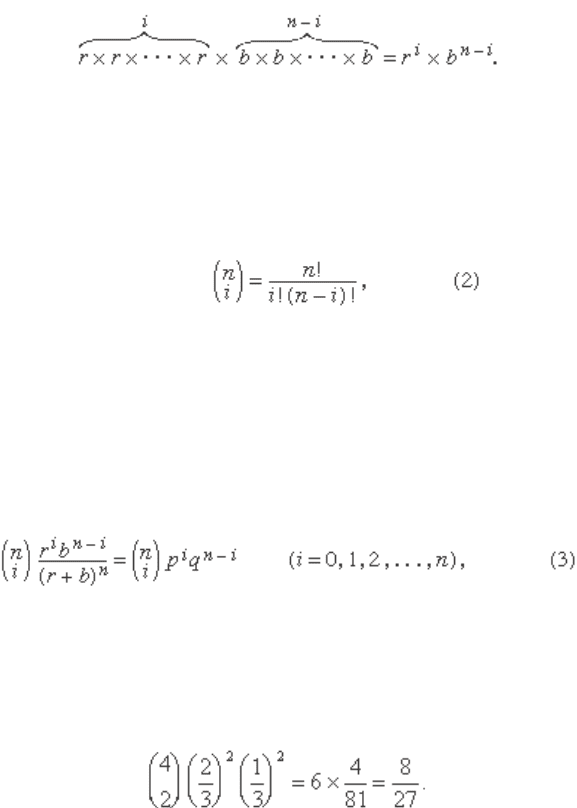
55
7
Probability Theory 7
the r + b balls is equally likely to be drawn and, because
each ball is replaced before the next draw, there are
( r + b ) ×⋯× ( r + b ) = ( r + b )
n
possible outcomes to the experi-
ment. Of these possible outcomes, the number that is
favourable to obtaining i red balls and n − i black balls in
any one particular order is
The number of possible orders in which i red balls and
n − i black balls can be drawn from the urn is the binomial
coeffi cient
where k ! = k × ( k − 1) ×⋯× 2 × 1 for positive integers k , and
0! = 1. Hence, the probability in question, which equals the
number of favourable outcomes divided by the number of
possible outcomes, is given by the binomial distribution
where p = r /( r + b ) and q = b /( r + b ) = 1 − p .
For example, suppose r = 2 b and n = 4. According to
equation (3), the probability of “exactly two red balls” is
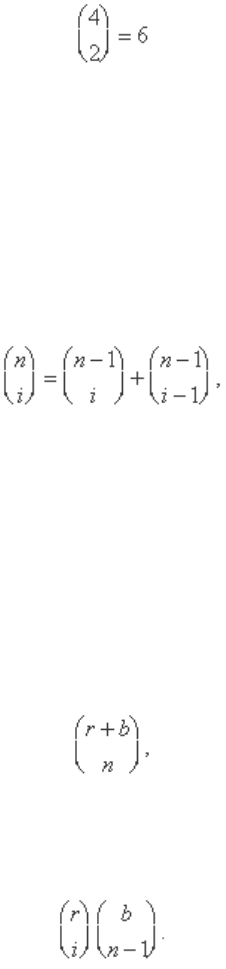
7 The Britannica Guide to Statistics and Probability 7
56
In this case the
possible outcomes are easily enumerated: (rrbb), (rbrb),
(brrb), (rbbr), (brbr), (bbrr). (For a derivation of equation
(2), observe that to draw exactly i red balls in n draws one
must either draw i red balls in the first n − 1 draws and a
black ball on the nth draw or draw i − 1 red balls in the
first n − 1 draws followed by the ith red ball on the nth
draw. Hence,
from which equation (2) can be verified by induction on n.)
Two related examples are (i) drawing without replace-
ment from an urn containing r red and b black balls and (ii)
drawing with or without replacement from an urn con-
taining balls of s different colours. If n balls are drawn
without replacement from an urn containing r red and b
black balls, the number of possible outcomes is
of which the number favourable to drawing i red and n − i
black balls is

57
7
Probability Theory 7
Hence, the probability of drawing exactly i red balls in
n draws is the ratio
If an urn contains balls of s different colours in the ratios
p
1
: p
2
: . . . : p
s
, where p
1
+⋯+ p
s
= 1 and if n balls are drawn with
replacement, then the probability of obtaining i
1
balls of
the fi rst colour, i
2
balls of the second colour, and so on is
the multinomial probability
The evaluation of equation (3) with pencil and paper
grows increasingly diffi cult with increasing n . It is even more
diffi cult to evaluate related cumulative probabilities—for
example the probability of obtaining “at most j red balls”
in the n draws, which can be expressed as the sum of equa-
tion (3) for i = 0, 1, . . . , j . The problem of approximate
computation of probabilities that are known in principle
is a recurrent theme throughout the history of probability
theory and will be discussed in more detail in the follow-
ing text.
The Birthday Problem
An entertaining example is to determine the probability
that in a randomly selected group of n people at least two
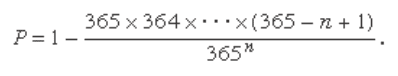
7 The Britannica Guide to Statistics and Probability 7
58
have the same birthday. If one assumes for simplicity that a
year contains 365 days and that each day is equally likely to
be the birthday of a randomly selected person, then in a
group of n people there are 365
n
possible combinations of
birthdays. The simplest solution is to determine the prob-
ability of no matching birthdays and then subtract this
probability from 1. Thus, for no matches, the fi rst person
may have any of the 365 days for his birthday, the second
any of the remaining 364 days for his birthday, the third any
of the remaining 363 days, . . . , and the n th any of the remain-
ing 365 − n + 1. The number of ways that all n people can have
different birthdays is then 365 × 364 ×⋯× (365 − n + 1), so that
the probability that at least two have the same birthday is
Numerical evaluation shows, rather surprisingly, that
for n = 23 the probability that at least two people have the
same birthday is about 0.5 (half the time). For n = 42 the
probability is about 0.9 (90 percent of the time).
This example illustrates that applications of proba-
bility theory to the physical world are facilitated by
assumptions that are not strictly true, but they should be
approximately true. Thus, the assumptions that a year
has 365 days and that all days are equally likely to be the
birthday of a random individual are false, because one
year in four has 366 days and because birth dates are irreg-
ularly distributed throughout the year. Moreover, if one
attempts to apply this result to an actual group of indi-
viduals, it is necessary to ask what it means for these to be
“randomly selected.” Naturally, it would be unreasonable
to apply it to a group known to contain twins. In spite of
the obvious failure of the assumptions to be literally true,

59
7
Probability Theory 7
as a classroom example, it rarely disappoints instructors
of classes having more than 40 students.
condiTional pRobabiliTy
Suppose two balls are drawn sequentially without replace-
ment from an urn containing r red and b black balls. The
probability of getting a red ball on the fi rst draw is r /( r + b ).
If, however, one is told that a red ball was obtained on the
fi rst draw, then the conditional probability of getting a red
ball on the second draw is ( r − 1)/( r + b − 1), because for the
second draw there are r + b − 1 balls in the urn, of which r − 1
are red. Similarly, if one is told that the fi rst ball drawn is
black, then the conditional probability of getting red on
the second draw is r /( r + b − 1).
In a number of trials the relative frequency with which
B occurs among those trials in which A occurs is just the
frequency of occurrence of A ∩ B divided by the fre-
quency of occurrence of A . This suggests that the
conditional probability of B given A (denoted P ( B | A ))
should be defi ned by
If A denotes a red ball on the fi rst draw and B a red ball
on the second draw in the experiment of the preceding
paragraph, P ( A ) = r /( r + b ) and
which is consistent with the “obvious” answer derived above.
