Greenwood D.T. Advanced Dynamics
Подождите немного. Документ загружается.

309 The central equation
where the ith particle velocity v
i
is given by (5.130). Thus, for the unconstrained kinetic
energy T (q,
˙
q, t), we obtain
∂T
∂
˙
q
k
=
n
i=1
m
i
v
i
·
∂v
i
∂
˙
q
k
=
N
i=1
m
i
v
i
· γ
ik
(5.138)
Then, from (5.127), (5.136), and (5.138), we find that
δ D =
n
k=1
∂T
∂
˙
q
k
d
dt
(δq
k
) −δ
˙
q
k
(5.139)
Let us consider the general case where the unconstrained kinetic energy is written in
terms of quasi-velocities, that is, let T = T
∗
(q, u, t). Then
δT
∗
=
n
i=1
∂T
∗
∂q
i
δq
i
+
n
j=1
∂T
∗
∂u
j
δu
j
(5.140)
where
δq
i
=
n
j=1
ij
δθ
j
(5.141)
δu
j
=
d
dt
(δθ
j
) −
d
dt
(δθ
j
) −δu
j
(5.142)
Thus,
δT
∗
=
n
j=1
∂T
∗
∂θ
j
δθ
j
+
∂T
∗
∂u
j
d
dt
(δθ
j
)
−
n
j=1
∂T
∗
∂u
j
d
dt
(δθ
j
) −δu
j
(5.143)
where we use the notation
∂T
∗
∂θ
j
=
n
i=1
∂T
∗
∂q
i
ij
( j = 1,...,n) (5.144)
The virtual work of the applied forces is
δW =
n
j=1
Q
r
δθ
r
(5.145)
where Q
r
is the applied generalized force associated with u
r
or δθ
r
.
Now let us integrate the central equation with respect to time over the fixed interval t
1
to t
2
. The system follows the actual path in q-space; and the δqs, which equal zero at the
end-points, satisfy the virtual constraints.
t
2
t
1
d
dt
(δ P) − δT
∗
− δW − δ D
dt = 0 (5.146)
First consider
t
2
t
1
d
dt
(δ P)dt = [δ P]
t
2
t
1
=
N
i=1
m
i
v
i
· δr
i
t
2
t
1
= 0 (5.147)

310 Equations of motion: integral approach
where we note that δr
i
= 0 at the end-points. Next, consider the integral of δT
∗
. We note
that, upon integrating the second term of (5.143) by parts, we obtain
t
2
t
1
n
j=1
∂T
∗
∂u
j
d
dt
(δθ
j
) dt =
n
j=1
∂T
∗
∂u
j
δθ
j
t
2
t
1
−
t
2
t
1
n
r=1
d
dt
∂T
∗
∂u
r
δθ
r
dt (5.148)
where the δθs equal zero at the end-points. Thus, we find that
t
2
t
1
δT
∗
dt =−
t
2
t
1
n
r=1
d
dt
∂T
∗
∂u
r
−
∂T
∗
∂θ
r
δθ
r
dt −
t
2
t
1
n
j=1
∂T
∗
∂u
j
d
dt
(δθ
j
) −δu
j
dt
(5.149)
Now we can write (5.146) in the form
t
2
t
1
n
r=1
d
dt
∂T
∗
∂u
r
−
∂T
∗
∂θ
r
− Q
r
δθ
r
+
n
j=1
∂T
∗
∂u
j
d
dt
(δθ
j
) −δu
j
−
n
i=1
∂T
∂
˙
q
i
d
dt
(δq
i
) −δ
˙
q
i
dt = 0 (5.150)
The end times t
1
and t
2
are arbitrary, so the integrand must equal zero continuously, resulting
in the general equation
n
r=1
d
dt
∂T
∗
∂u
r
−
∂T
∗
∂θ
r
− Q
r
δθ
r
+
n
j=1
∂T
∗
∂u
j
d
dt
(δθ
j
) −δu
j
−
n
i=1
∂T
∂
˙
q
i
d
dt
(δq
i
) −δ
˙
q
i
= 0 (5.151)
Up to this point, no assumptions have been made concerning the transpositional terms in
(5.151). But now let us assume that
d
dt
(δθ
j
) −δu
j
= 0(j = 1,...,n) (5.152)
Furthermore, let us apply the m virtual constraints by letting δθ
r
= 0forr =
n − m + 1,...,n. The remaining (n − m) δθsareindependent. Then we obtain
the explicit form of the central equation:
n−m
r=1
d
dt
∂T
∗
∂u
r
−
∂T
∗
∂θ
r
− Q
r
δθ
r
−
n
i=1
∂T
∂
˙
q
i
d
dt
(δq
i
) −δ
˙
q
i
= 0 (5.153)
Notice that this result is similar to (5.101), the transpositional form of the Boltzmann–
Hamel equation.
The (n − m) differential equations of motion are obtained by writing the last term of
(5.153) as a function of the δθs, and then setting the coefficient of each δθ
r
in (5.153)
equal to zero. As mentioned earlier, the kinetic energy T
∗
(q, u, t) may be written for the
311 The central equation
constrained system, that is, the order of differentiation and the application of constraints
makes no difference in this case. But the kinetic energy T (q,
˙
q, t) must be written for the
unconstrained system.
The Boltzmann–Hamel equation can be derived from the general result given in (5.151).
Let us begin by first noting that
∂T
∂
˙
q
i
=
n
j=1
∂T
∗
∂u
j
ji
(i = 1,...,n) (5.154)
and then recalling from (5.47) that
d
dt
(δθ
j
) −δu
j
−
n
i=1
ji
d
dt
(δq
i
) −δ
˙
q
i
=
n
i=1
n
k=1
∂
ji
∂q
k
−
∂
jk
∂q
i
˙
q
k
δq
i
+
n
i=1
∂
ji
∂t
−
∂
jt
∂q
i
δq
i
( j = 1,...,n) (5.155)
Moreover,
˙
q
k
=
n
l=1
kl
u
l
+
kt
(k = 1,...,n) (5.156)
δq
i
=
n
r=1
ir
δθ
r
(i = 1,...,n) (5.157)
Then (5.151) takes the form
n
r=1
d
dt
∂T
∗
∂u
r
−
∂T
∗
∂θ
r
− Q
r
+
n
i=1
n
j=1
n
k=1
∂T
∗
∂u
j
∂
ji
∂q
k
−
∂
jk
∂q
i
×
n
l=1
kl
u
l
+
kt
ir
+
n
i=1
n
j=1
∂T
∗
∂u
j
∂
ji
∂t
−
∂
jt
∂q
i
ir
δθ
r
= 0 (5.158)
Now apply the instantaneous constraints by setting δθ
r
= 0forr = n − m + 1,...,n.
The remaining (n − m) δθsareindependent so each coefficient must equal zero. Thus we
obtain
d
dt
∂T
∗
∂u
r
−
∂T
∗
∂θ
r
+
n
i=1
n
j=1
n
k=1
n
l=1
∂T
∗
∂u
j
∂
ji
∂q
k
−
∂
jk
∂q
i
kl
ir
u
l
+
n
i=1
n
j=1
n
k=1
∂T
∗
∂u
j
∂
ji
∂q
k
−
∂
jk
∂q
i
kt
ir
+
n
i=1
n
j=1
∂T
∗
∂u
j
∂
ji
∂t
−
∂
jt
∂q
i
ir
= Q
r
(r = 1,...,n − m) (5.159)

312 Equations of motion: integral approach
This is a detailed form of the Boltzmann–Hamel equation, as in (4.82). Here the derivation
involves an integral method using the central equation. We note from (5.155) that, in spite
of transpositional terms in the integral expressed in (5.150), the varied path is actually
determined by δqsorδθs which satisfy the virtual constraints.
Example 5.3 A thin uniform disk of mass m and radius r rolls without slipping on the
horizontal xy-plane (Fig. 5.5). Let us find the differential equations of motion, using the
explicit central equation, namely,
n−m
r=1
d
dt
∂T
∗
∂u
r
−
∂T
∗
∂θ
r
− Q
r
δθ
r
−
n
i=1
∂T
∂
˙
q
i
d
dt
(δq
i
) −δ
˙
q
i
= 0 (5.160)
As generalized coordinates, let us choose (φ,θ,ψ,x, y) where (φ, θ,ψ) are Euler angles
and where (x , y) is the location of the contact point C. The independent usare(ω
d
,
˙
θ,).
There are two additional us that are set equal to zero to represent the nonholonomic con-
straints. Thus, we have
u
1
= ω
d
=
˙
φ sin θ (5.161)
u
2
=
˙
θ (5.162)
u
3
= =
˙
φ cos θ +
˙
ψ (5.163)
u
4
= r
˙
ψ cos φ +
˙
x = 0 (5.164)
u
5
= r
˙
ψ sin φ +
˙
y = 0 (5.165)
x
φ
φ
θ
z
y
m
(x, y)
r
d
.
.
⍀
ψ
C
Figure 5.5.

313 The central equation
The two constraint equations state that there is no slipping at the contact point C. With this
assumption, the contact point moves with a speed r
˙
ψ on the xy-plane. The rotations
˙
φ and
˙
θ occur about C and do not cause it to move.
The constrained kinetic energy T
∗
(q, u) is equal to the sum of the translational and
rotational portions. We obtain
T
∗
=
1
2
mr
2
(
˙
θ
2
+
2
) +
1
2
mr
2
2
2
+
1
2
mr
2
4
ω
2
d
+
˙
θ
2
=
1
8
mr
2
u
2
1
+
5
8
mr
2
u
2
2
+
3
4
mr
2
u
2
3
(5.166)
where we note that the moments of inertia about the center are
I
a
=
1
2
mr
2
, I
t
=
1
4
mr
2
(5.167)
The unconstrained kinetic energy T (q,
˙
q) is more complicated. Again we sum the trans-
lational and rotational parts, obtaining
T =
1
2
m[(
˙
x −r
˙
φ cos φ cos θ + r
˙
θ sin φ sin θ)
2
+ (
˙
y −r
˙
φ sin φ cos θ − r
˙
θ cos φ sin θ)
2
+r
2
˙
θ
2
cos
2
θ] +
1
8
mr
2
(
˙
φ
2
sin
2
θ +
˙
θ
2
) +
1
4
mr
2
(
˙
φ cos θ +
˙
ψ)
2
=
1
8
mr
2
˙
φ
2
(1 +5 cos
2
θ) +
5
8
mr
2
˙
θ
2
+
1
4
mr
2
˙
ψ
2
+
1
2
m(
˙
x
2
+
˙
y
2
)
+
1
2
mr
2
˙
φ
˙
ψ cos θ − mr
˙
φ
˙
x cos φ cos θ + mr
˙
θ
˙
x sin φ sin θ
−mr
˙
φ
˙
y sin φ cos θ − mr
˙
θ
˙
y cos φ sin θ (5.168)
We wish to express the last term of (5.160) in terms of us and δθs. If (5.161)–(5.165) are
solved for the
˙
qs, the result is
˙
φ = u
1
csc θ (5.169)
˙
θ = u
2
(5.170)
˙
ψ =−u
1
cot θ + u
3
(5.171)
˙
x = ru
1
cos φ cot θ − ru
3
cos φ + u
4
(5.172)
˙
y = ru
1
sin φ cot θ − ru
3
sin φ + u
5
(5.173)
where u
4
= u
5
= 0. Similarly,
δφ = csc θδθ
1
(5.174)
δθ = δθ
2
(5.175)
δψ =−cot θδθ
1
+ δθ
3
(5.176)
δx = r cos φ cot θδθ
1
−r cos φδθ
3
(5.177)
δy = r sin φ cot θδθ
1
−r sin φδθ
3
(5.178)
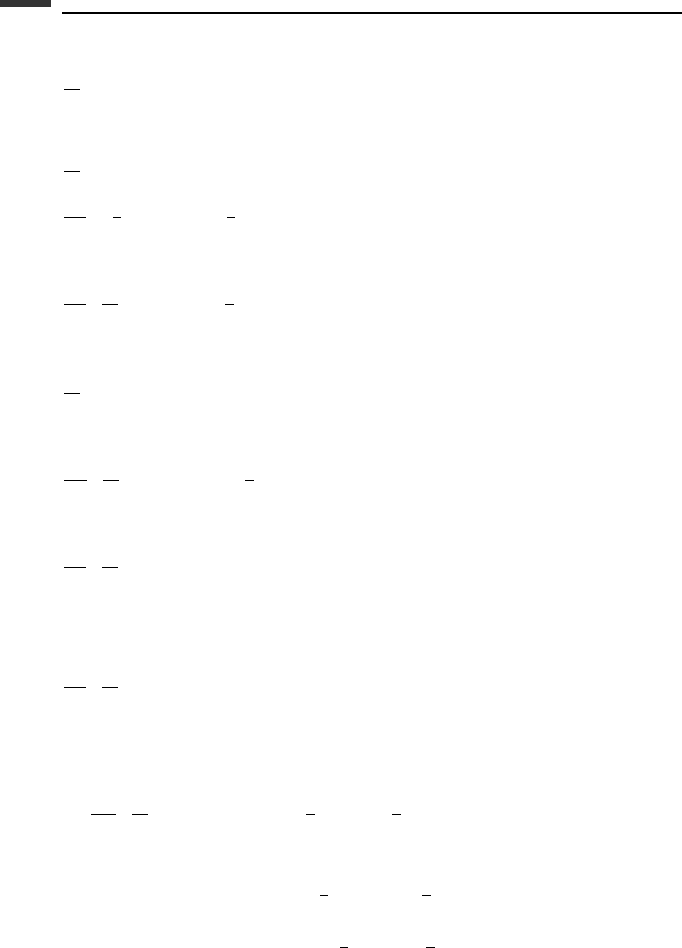
314 Equations of motion: integral approach
In addition we assume that, for all j ,
d
dt
(δθ
j
) −δu
j
= 0 (5.179)
Then we find that
d
dt
(δφ) −δ
˙
φ = csc θ cot θ (u
1
δθ
2
− u
2
δθ
1
) (5.180)
∂T
∂
˙
φ
=
1
4
mr
2
u
1
sin θ +
3
2
mr
2
u
3
cos θ (5.181)
and therefore
∂T
∂
˙
φ
d
dt
(δφ) − δ
˙
φ
=
1
4
mr
2
cot θ(u
1
+ 6u
3
cot θ)(u
1
δθ
2
− u
2
δθ
1
) (5.182)
Since (5.162) is integrable and (5.179) applies, we obtain
d
dt
(δθ) − δ
˙
θ = 0 (5.183)
Similarly, we find that
∂T
∂
˙
ψ
d
dt
(δψ) −δ
˙
ψ
=−
1
2
mr
2
u
3
csc
2
θ(u
1
δθ
2
− u
2
δθ
1
) (5.184)
and
∂T
∂
˙
x
d
dt
(δx ) − δ
˙
x
=mr
2
(u
2
sin φ cos φ csc θ − u
3
cos
2
φ csc
2
θ)(u
1
δθ
2
− u
2
δθ
1
)
+mr
2
(u
2
sin
2
φ − u
3
sin φ cos φ csc θ)(u
1
δθ
3
− u
3
δθ
1
) (5.185)
Furthermore,
∂T
∂
˙
y
d
dt
(δy) − δ
˙
y
=−mr
2
(u
2
sin φ cos φ csc θ + u
3
sin
2
φ csc
2
θ)(u
1
δθ
2
− u
2
δθ
1
)
+mr
2
(u
2
cos
2
φ + u
3
sin φ cos φ csc θ)(u
1
δθ
3
− u
3
δθ
1
) (5.186)
Adding (5.182)–(5.186), we obtain
5
i=1
∂T
∂
˙
q
i
d
dt
(δq
i
) −δ
˙
q
i
= mr
2
1
4
u
1
cot θ −
3
2
u
3
(u
1
δθ
2
− u
2
δθ
1
)
+mr
2
u
2
(u
1
δθ
3
− u
3
δθ
1
)
= mr
2
−
1
4
u
1
u
2
cot θ +
1
2
u
2
u
3
δθ
1
+mr
2
1
4
u
2
1
cot θ −
3
2
u
1
u
3
δθ
2
+mr
2
u
1
u
2
δθ
3
(5.187)
315 Suslov’s principle
Referring to (5.166), we have
n
r=1
d
dt
∂T
∗
∂u
r
−
∂T
∗
∂θ
r
− Q
r
δθ
r
=
1
4
mr
2
˙
u
1
δθ
1
+
5
4
mr
2
˙
u
2
+ mgr cos θ
δθ
2
+
3
2
mr
2
˙
u
3
δθ
3
(5.188)
where
Q
1
= 0, Q
2
=−mgr cos θ, Q
3
= 0 (5.189)
Finally, using the explicit form of the central equation, we obtain the equations of motion.
The u
1
equation, found by setting the coefficient of δθ
1
equal to zero, is
1
4
mr
2
˙
u
1
+
1
4
mr
2
u
1
u
2
cot θ −
1
2
mr
2
u
2
u
3
= 0 (5.190)
Similarly, the u
2
equation is
5
4
mr
2
˙
u
2
−
1
4
mr
2
u
2
1
cot θ +
3
2
mr
2
u
1
u
3
=−mgr cos θ (5.191)
The u
3
equation is
3
2
mr
2
˙
u
3
− mr
2
u
1
u
2
= 0 (5.192)
Using the original notation for angular velocity components, we can write the equations
of motion as follows:
1
4
mr
2
˙ω
d
+
1
4
mr
2
ω
d
˙
θ cot θ −
1
2
mr
2
˙
θ = 0 (5.193)
5
4
mr
2
¨
θ −
1
4
mr
2
ω
2
d
cot θ +
3
2
mr
2
ω
d
=−mgr cos θ (5.194)
3
2
mr
2
˙
− mr
2
ω
d
˙
θ = 0 (5.195)
These equations are identical with (4.259)–(4.261) obtained earlier.
5.5 Suslov’s principle
Dependent and independent coordinates
Thus far, we have assumed that the linear nonholonomic constraint equations have the form
n
i=1
a
ji
(q, t)
˙
q
i
+ a
jt
(q, t) = 0(j = 1,...,m) (5.196)
This form has the characteristic that all the qs are treated equally. Now let us change
the viewpoint and arbitrarily designate m of the qsasdependent; whereas, the remaining
316 Equations of motion: integral approach
(n − m) qs are termed independent. Equation (5.196) can be solved for the dependent
˙
q
D
s
in terms of the independent
˙
q
I
s. We obtain m nonholonomic constraint equations written
in the form
˙
q
D
=
n−m
I =1
B
DI
(q, t)
˙
q
I
+ B
Dt
(q, t)(D = n − m + 1,...,n) (5.197)
or, more briefly,
˙
q
D
= φ
D
(q,
˙
q
I
, t)(D = n − m + 1,...,n) (5.198)
Suslov’s principle
Let us begin with the general nonholonomic form of Hamilton’s principle, namely,
t
2
t
1
(δT + δW )dt = 0 (5.199)
where each varied path satisfies the virtual constraints, and the δqs are equal to zero at the
end-points in extended q-space (Fig. 5.1).
Now introduce the constrained kinetic energy T
0
(q,
˙
q
I
, t) which is obtained from the
unconstrained kinetic energy T (q,
˙
q, t) by substituting for the
˙
q
D
s using the constraint equa-
tions (5.197). For any realizable motion, the energies T
0
and T are equal. Their variations
δT
0
and δT are not equal, however. To see how this comes about, consider
δT =
n
i=1
∂T
∂q
i
δq
i
+
n
i=1
∂T
∂
˙
q
i
δ
˙
q
i
(5.200)
For a given varied path, we can take
d
dt
(δq
i
) −δ
˙
q
i
= 0(i = 1,...,n) (5.201)
and therefore we obtain that, in (5.199),
δT =
n
i=1
∂T
∂q
i
δq
i
+
n
i=1
∂T
∂
˙
q
i
d
dt
(δq
i
) (5.202)
For the constrained system, however, we know that at least m of the transpositional expres-
sions of (5.201) must be nonzero. Let us assume that
d
dt
(δq
I
) −δ
˙
q
I
= 0(I = 1,...,n − m) (5.203)
d
dt
(δq
D
) −δ
˙
q
D
= 0(D = n − m + 1,...,n) (5.204)
where
δ
˙
q
D
= δφ
D
=
n
i=1
∂φ
D
∂q
i
δq
i
+
n−m
I =1
∂φ
D
∂
˙
q
I
δ
˙
q
I
(5.205)

317 Suslov’s principle
Then we see that
δT
0
=
n
i=1
∂T
∂q
i
δq
i
+
n−m
I =1
∂T
∂
˙
q
I
d
dt
(δq
I
) +
n
D=n−m+1
∂T
∂
˙
q
D
δ
˙
q
D
(5.206)
A comparison of (5.202) and (5.206) results in
δT = δT
0
+
n
D=n−m+1
∂T
∂
˙
q
D
d
dt
(δq
D
) −δ
˙
q
D
(5.207)
Now substitute the expression for δT from (5.207) into (5.199) which is Hamilton’s
principle. The result is
t
2
t
1
δT
0
+ δW +
n
D=n−m+1
∂T
∂
˙
q
D
d
dt
(δq
D
) −δ
˙
q
D
dt = 0 (5.208)
This is Suslov’s principle.
The virtual work is
δW =
n
i=1
Q
i
δq
i
=
n−m
I =1
Q
I
δq
I
+
n
D=n−m+1
Q
D
δq
D
(5.209)
where the Qs are generalized applied forces for the case of unconstrained δqs. We actually
have constrained δqs, however, with
δq
D
=
n−m
I =1
B
DI
δq
I
(5.210)
Hence, the virtual work becomes
δW =
n−m
I =1
Q
I
δq
I
+
n−m
I =1
n
D=n−m+1
Q
D
B
DI
δq
I
(5.211)
or
δW =
n−m
I =1
Q
0
I
δq
I
(5.212)
where the generalized applied force associated with q
I
in the constrained system is
Q
0
I
= Q
I
+
n
D=n−m+1
Q
D
B
DI
(I = 1,...,n − m) (5.213)
Equations of motion
To obtain the differential equations of motion from Suslov’s principle, first let us write
δT
0
=
n−m
I =1
∂T
0
∂q
I
δq
I
+
n
D=n−m+1
∂T
0
∂q
D
δq
D
+
n−m
I =1
∂T
0
∂
˙
q
I
d
dt
(δq
I
) (5.214)

318 Equations of motion: integral approach
where we have used (5.203). Now integrate δT
0
with respect to time, using integration by
parts on the last term and noting that δq
I
vanishes at t
1
and t
2
. Upon multiplying by −1 and
recalling (5.210), the integral of (5.208) can be written in the form
t
2
t
1
n−m
I =1
d
dt
∂T
0
∂
˙
q
I
−
∂T
0
∂q
I
+
n
D=n−m+1
∂T
0
∂q
D
B
DI
− Q
0
I
δq
I
−
n
D=n−m+1
∂T
∂
˙
q
D
d
dt
(δq
D
) −δ
˙
q
D
dt = 0 (5.215)
The transpositional term can be written as a homogeneous linear expression in the δq
I
s
which are independent. Hence, the integrand must vanish for all t, resulting in the explicit
form of Suslov’s principle:
n−m
I =1
d
dt
∂T
0
∂
˙
q
I
−
∂T
0
∂q
I
+
n
D=n−m+1
∂T
0
∂q
D
B
DI
− Q
0
I
δq
I
−
n
D=n−m+1
∂T
∂
˙
q
D
d
dt
(δq
D
) −δ
˙
q
D
= 0 (5.216)
The equations of motion are obtained by expressing the last term in terms of δq
I
s and then
equating to zero the coefficient of each δq
I
. This results in (n − m) second-order differential
equations. There are also m kinematical constraint equations, giving a total of n equations
to solve for the nqs.
Comparing this result with the explicit central equation, (5.153), we see that the Suslov
equation has the advantage that the last summation is over the m dependent
˙
qs only rather
than over the complete set of n. On the other hand, Suslov’s equation has the possible
disadvantage that it does not allow quasi-velocities to be used.
Example 5.4 As an example of the application of Suslov’s equation (5.216), consider
the motion of a dumbbell with a knife-edge constraint sliding on the horizontal xy-plane
(Fig. 5.6). As generalized coordinates, let us choose (φ, x , y), where (φ, x) are considered
independent and y is dependent.
The nonholonomic constraint equation is
˙
q
D
=
˙
y =
˙
x tan φ (5.217)
and the corresponding virtual constraint is
δq
D
= δy = δx tan φ (5.218)
The unconstrained kinetic energy, from (1.127), is
T = m(
˙
x +
˙
y
2
) +
1
2
ml
2
˙
φ
2
+ ml
˙
φ(−
˙
x sin φ +
˙
y cos φ) (5.219)
