Greenwood D.T. Advanced Dynamics

Подождите немного. Документ загружается.

319 Suslov’s principle

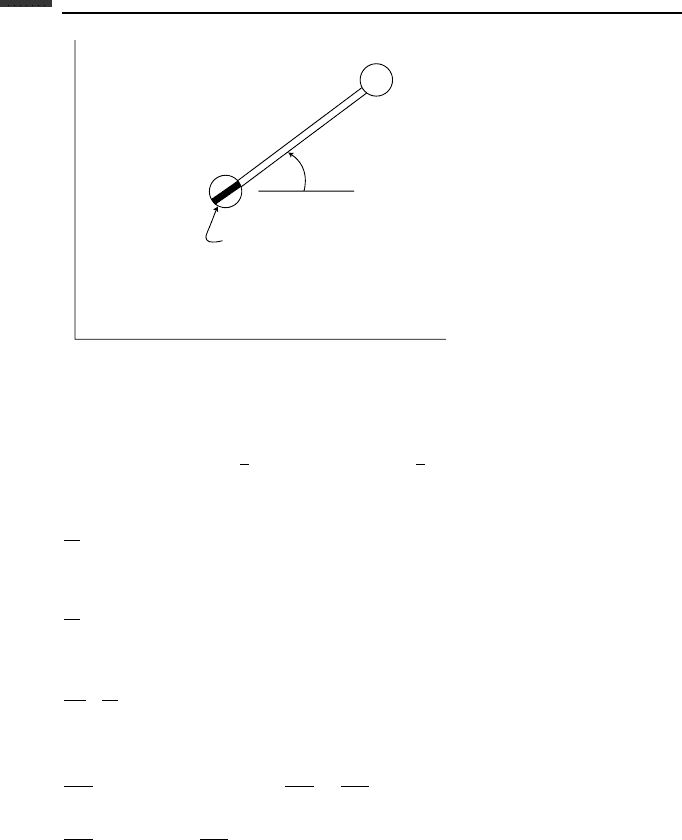
(x, y)

Figure 5.6.

The constrained kinetic energy, upon substitution from (5.217), is

= m(1 + tan

φ)

= m

sec

φ +

(5.220)

We see that

(δy) − δ

y = sec

φ (

φδx −

xδφ) (5.221)

where we note from (5.203) that

(δx ) − δ

x = 0 (5.222)

Then, using (5.217), we obtain

∂T

∂



(δy) − δ



= (2m

x tan φ + ml

φ cos φ)sec

φ (

φδx −

xδφ) (5.223)

Differentiation of the constrained kinetic energy yields

∂T

∂φ

= 2m

sec

φ tan φ,

∂T

∂x

∂T

∂y

= 0 (5.224)

∂T

∂

= ml

φ,

∂T

∂

= 2m

x sec

φ (5.225)

Also,

= 0, Q

= 0 (5.226)

Finally, a substitution in Suslov’s equation, (5.216), results in

(ml

φ + ml

x sec φ)δφ + (2m

x +2m

x tan φ − ml

cos φ)sec

φδx = 0 (5.227)

320 Equations of motion: integral approach

The virtual displacements δφ and δx are arbitrary and sec

φ is not equal to zero, so each

coefﬁcient must equal zero. Thus, we obtain the equations of motion

φ + ml

x sec φ = 0 (5.228)

x +2m

x tan φ − ml

cos φ = 0 (5.229)

Note that

x sec φ is equal to the longitudinal velocity component of the particles, that is,

the velocity along the rod.

These equations of motion agree with (4.31) and (4.32) of Example 4.1 on page 220,

obtained using Maggi’s equation, if one substitutes the differentiated constraint equation,

namely

y =

x tan φ +

x sec

φ (5.230)

Example 5.5 A uniform disk of mass m and radius r rolls without slipping on the horizontal

xy-plane (Fig. 5.7). We wish to obtain the equations of motion using the Suslov equation,

(5.216).

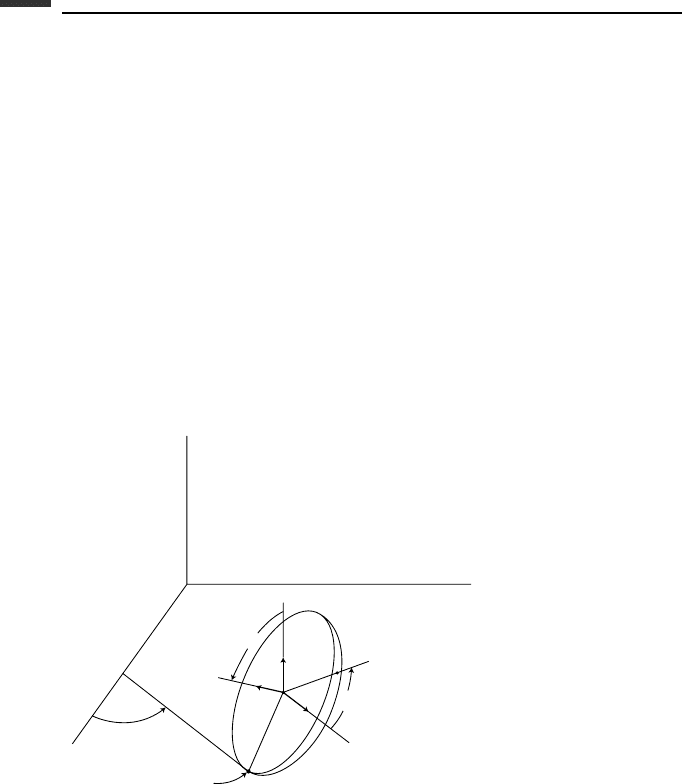
(x, y)

␺

␾

␪

Figure 5.7.

The conﬁguration of the system is given by the location of the contact point C and the

Euler angles. Thus, we can choose (φ,θ,ψ, x , y) as generalized coordinates, with the ﬁrst

three as independent q

s and the last two as dependent q

s. The constraint equations of the

form

= φ

(q,

)are

x =−r

ψ cos φ (5.231)

y =−r

ψ sin φ (5.232)

321 Suslov’s principle

and the corresponding virtual displacements are

δx =−r cos φδψ (5.233)

δy =−r sin φδψ (5.234)

The unconstrained kinetic energy is equal to that due to the translation of the center of

mass, plus that due to rotation about the center of mass. Thus, we obtain

T =

m[(

x cos φ +

y sin φ − r

φ cos θ )

+(−

x sin φ +

y cos φ − r

θ sin θ )

cos

θ]

(

sin

θ +

) +

(

φ cos θ +

ψ)

(1 +5 cos

θ) +

)

ψ cos θ − mr

φ cos θ (

x cos φ +

y sin φ)

+mr

θ sin θ (

x sin φ −

y cos φ) (5.235)

The constrained kinetic energy, obtained by substituting the constraint equations for

x and

y into (5.235), is

(1 +5 cos

θ) +

ψ cos θ (5.236)

This assumes that there is no slipping at the contact point C.

The generalized applied forces for the constrained system are

= 0, Q

=−mgr cos θ, Q

= 0 (5.237)

In accordance with (5.203), we have

(δφ) −δ

φ = 0,

(δθ) − δ

θ = 0,

(δψ) −δ

ψ = 0 (5.238)

Then, differentiation of (5.231) and (5.233) results in

(δx ) − δ

x = r sin φ(

φδψ −

ψδφ) (5.239)

Similarly,

(δy) − δ

y =−r cos φ(

φδψ −

ψδφ) (5.240)

Furthermore,

∂T

∂

= m

x −mr

φ cos φ cos θ + mr

θ sin φ sin θ

=−mr

φ cos φ cos θ + mr

θ sin φ sin θ − mr

ψ cos φ (5.241)

322 Equations of motion: integral approach

and

∂T

∂

=−mr

φ sin φ cos θ − mr

θ cos φ sin θ − mr

ψ sin φ (5.242)

Hence, we ﬁnd that

∂T

∂



(δx ) − δ



∂T

∂



(δy) − δ



= mr

θ sin θ (

φδψ −

ψδφ) (5.243)

To obtain the φ equation of motion, we ﬁrst evaluate



∂T

∂



−

∂T

∂φ

φ(1 +5 cos

θ) +

ψ cos θ

−

θ sin θ cos θ −

ψ sin θ (5.244)

Then, using Suslov’s equation, the coefﬁcient of δφ is the φ equation:

φ(1 +5 cos

θ) +

ψ cos θ −

θ sin θ cos θ

−

ψ sin θ = 0 (5.245)

Next, we obtain



∂T

∂



−

∂T

∂θ

θ +

sin θ cos θ +

ψ sin θ (5.246)

and the θ equation is

θ +

sin θ cos θ +

ψ sin θ =−mgr cos θ (5.247)

Finally,



∂T

∂



−

∂T

∂ψ

ψ +

φ cos θ −

θ sin θ (5.248)

and the ψ equation is

ψ +

φ cos θ −

θ sin θ = 0 (5.249)

These equations of motion are equivalent to those obtained in Example 4.2 on page 222

using Maggi’s equation, but the Suslov approach is simpler and more direct.

5.6 Summary of integral methods

A review of integral methods in the analysis of nonholonomic systems must begin with

Hamilton’s principle, namely,



(δT + δW )dt = 0 (5.250)

323 Bibliography

Here the kinetic energy T (q,

q, t) is unconstrained and

δT =



i=1

∂T

∂q

δq



i=1

∂T

∂

(δq

) (5.251)

since we assume that

(δq

) −δ

= 0 (5.252)

Furthermore, the varied path determined by the δqs satisﬁes the virtual constraints of (5.4)

but does not satisfy, in general, the actual constraints of (5.11).

Hamilton’s principle leads to equations of motion of the form given by Lagrange’s prin-

ciple or Maggi’s equation.

The other integral methods can be derived directly from Hamilton’s principle. For exam-

ple, if the kinetic energy in terms of quasi-velocities is T

∗

(q, u, t) and we use the substitution

δT = δT

∗



i=1

∂T

∂



(δq

) −δ



(5.253)

in (5.250), the result after integration by parts reduces to the explicit form of the central

equation, (5.153).

On the other hand, if we designate the qs as either independent or dependent, and write

the constrained kinetic energy T

(q,

, t), then the substitution

δT = δT



D=n−m+1

∂T

∂



(δq

) −δ



(5.254)

in (5.250) results in the explicit form of Suslov’s principle, (5.216). Here we assume that

(δq

) −δ

= 0(I = 1,...,n − m) (5.255)

All these methods utilize varied paths, determined by the δqs, which satisfy the virtual

constraints but not the actual constraints. Furthermore, for a given system and varied path,

the integrals used in the various methods will all be equal to δ P at any given time t ,

where t

< t < t

. Thus, differing notation and variables are being used to express the same

basic integral of Hamilton’s principle. The differing approaches, however, can result in one

method being easier than another, depending upon the particular system being analyzed.

5.7 Bibliography

Greenwood, D. T. Classical Dynamics. Meneola, NY: Dover Publications, 1997.

Lanczos, C. The Variational Principles of Mechanics. Toronto: University of Toronto Press, 1949.

Neimark, Ju.I. and Fufaev, N. A. Dynamics of Nonholonomic Systems. Translations of Mathematical

Monographs, Vol. 33. Providence, RI: American Mathematical Society, 1972.

Papastavridis, J. G. Analytical Mechanics. Oxford: Oxford University Press, 2002.

Pars, L. A. A Treatise on Analytical Dynamics. London: William Heinemann, 1965.

324 Equations of motion: integral approach

5.8 Problems

5.1. Consider the nonholonomic form of Hamilton’s principle, as given by (5.27). Show

that the integral



(δT + δW )dt

where t

< t < t

, is equal to δ P of the central equation (5.129).

5.2. (a) Show that, for a system of N particles,

δ P =



j=1

∂T

∗

∂u

δθ

where T

∗

(q, u, t) is the unconstrained kinetic energy written in terms of quasi-

velocities. (b) Starting with the central equation in the form of (5.129), and without

using the ﬁxed end-points and integration by parts of the integral method, derive

(5.151) and the explicit form of the central equation.

5.3. A nonholonomic system has m constraints that are expressed in the dependent form

n−m



i=1

(q)

(k = n − m + 1,...,n)

Assuming that the independent qs satisfy

(δq

) −δ

= 0(i = 1,...,n − m)

show that, for the dependent qs,

(δq

) −δ

n−m



i=1

n−m



j=1

δq

(k = n − m + 1,...,n)

where

∂ B

∂q

−

∂ B

∂q



l=n−m+1



∂ B

∂q

−

∂ B

∂q



A substitution of this result into the Suslov equation (5.216) results in Voronets’

equation:



∂T

∂



−



∂T

∂q



k=n−m+1

∂T

∂q



−

n−m



j=1



k=n−m+1

∂T

∂

= Q

where

= Q



k=n−m+1

(i = 1,...,n − m)

325 Problems

5.4. Consider the rotational motion of a rigid body using (ω

,ω

) as quasi-velocities,

where xyz is a body-ﬁxed principal axis system at the center of mass. (a) Use classical

Euler angles as qs and show that

(δθ

) −δω

= ω

δθ

− ω

δθ

and similarly for the y and z components. (b) Use the central equation in the general

form of (5.151) to derive the Euler equations of rotational motion. Assume that

d/dt (δq

) −δ

= 0 for each of the Euler angles.

5.5. A pair of wheels, each considered to be a thin uniform disk of mass m and radius

r, are connected by a massless axle of length L. They roll without slipping on the

xy-plane which is inclined at an angle α from the horizontal. The independent usare

(v,

φ) where v is the speed of the center of mass, and

φ is the angular velocity of the

axle. The qsare(x, y,φ,ψ

,ψ

). (a) Use the explicit form of the central equation

to obtain the differential equations of motion. (b) Assume the initial conditions are

v(0) = v

, φ(0) = 0,

φ(0) = ω

. Solve for

x and

y as functions of time and ﬁnd their

average values.

(x, y)

␺

⭈

␺

⭈

Figure P 5.5.

5.6. A dumbbell consists of two particles, each of mass m, connected by a massless rod of

length l (Fig. P 5.6). Particle 1 has a knife-edge constraint oriented perpendicular to the

rod. A constant force F = Fi is applied at particle 2. (a) Use (x, y,φ) as generalized

coordinates and obtain the differential equations of motion from the explicit form of

Suslov’s principle. Let x be the dependent coordinate. (b) Show that the speed v of

particle 1 is constant. (c) Show that the angle φ obeys a differential equation of the

same form as for a simple pendulum, even though particle 1 is moving.

326 Equations of motion: integral approach

(x, y)

Figure P 5.6.

5.7. Consider a holonomic system with nqs and m constraints of the form

= 

, t)

where I = 1,...,n − m and D = n − m + 1,...,n. Show that, for this system, the

explicit form of Suslov’s principle reduces to the fundamental form of Lagrange’s

equation.

5.8. Two dumbbells, each having a massless rod of length l, are connected by a joint to

form particle 3 of mass 2m. The system moves on the horizontal xy-plane. Particles 1

and 2 have knife-edge constraints requiring that the quasi-velocities u

and u

equal

zero. Let the qsbe(x, y,ψ,φ); the independent quasi-velocities are (u

, u

). Use the

explicit form of the central equation to obtain the differential equations of motion.

(x, y)

ψ − φ

ψ + φ

c.m.

Figure P 5.8.

327 Problems

5.9. Consider again the system of Problem 5.8. Choose (x, y) as dependent qs and (ψ, φ)as

independent qs. (a) Find the unconstrained kinetic energy T (q,

q) and the constrained

kinetic energy T

(q,

). (b) Use the explicit form of Suslov’s principle to obtain the

differential equations of motion.

5.10. A disk of mass 2m, radius r , and central moment of inertia I has a knife-edge

constraint at its center C. A particle of mass m is connected by a massless rod of

length l to a point P on the circumference by means of a joint. The system moves

on the horizontal xy-plane. Using (θ,φ, x, y)asqs and (v,

θ,

φ)asus, obtain the

differential equations of motion by means of the explicit central equation.

(x, y)

Figure P 5.10.

5.11. A thin uniform disk of mass m and radius r is constrained to remain vertical as

it rolls on the horizontal xy-plane (Fig. P 5.11). A series of knife edges are em-

bedded in the xy-plane and are aligned parallel to the x-axis. As a result, the

contact point P on the disk cannot slip in the y direction, but can slide with-

out friction in the x direction. Let θ be the angle between the plane of the disk

and the vertical yz-plane. Choose (θ,ψ, x, y)asqs and (

θ,

ψ,

x) as indepen-

dent

qs, where

ψ is the rotation rate about the axis of symmetry. (a) Use the

explicit form of Suslov’s principle to obtain the differential equations of mo-

tion. (b) Assume the initial conditions θ(0) = 0,

θ(0) =

ψ(0) =

x(0) =

. Find the minimum and maximum values of

ψ and of the speed v of the

center C.

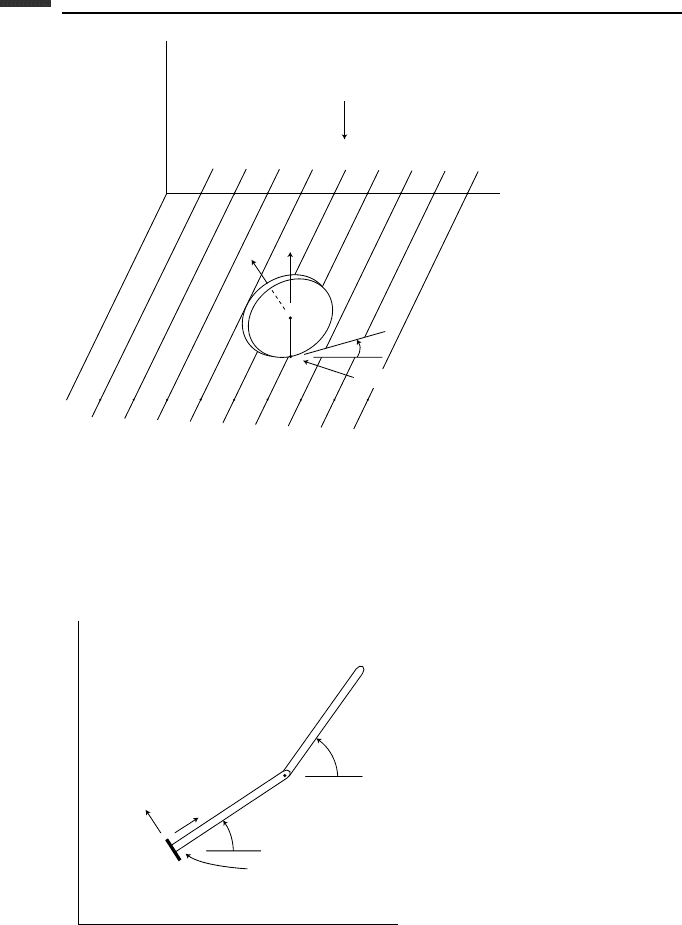
328 Equations of motion: integral approach

(x, y)

␺

⭈

Figure P 5.11.

5.12. Two rods, each of mass m and length l, are connected by a joint at B and move in the

horizontal xy-plane. A knife-edge constraint at A permits no velocity component w

along the rod at A but allows a perpendicular component v. Choose (θ

,θ

, x, y)as

qs and (

,v,w)asus. Obtain the differential equations of motion by using the

transpositional form of the Boltzmann–Hamel equation.

(x, y)

Figure P 5.12.