Greenwood D.T. Advanced Dynamics

Подождите немного. Документ загружается.

339 Numerical integration

numbers, in a relative sense. By subtracting the nearly equal numbers, one can lose many

signiﬁcant digits. Furthermore, roundoff errors become relatively more important if the

truncation errors are drastically reduced by using a very small step size.

To illustrate the nature of roundoff errors, suppose we are given y = e

and we desire

to calculate y

n+1

− y

for the case t

= 10 and h = 0.001. If one uses a calculator which

employs ten decimal digits, the result is

10.001

− e

= 22048.50328 − 22026.46579

= 22.03749

We notice that, although the numbers to be subtracted are given to ten signiﬁcant digits, the

result has only seven signiﬁcant digits, and there is some doubt concerning the accuracy

of the last digit. In order to avoid errors due to the small difference of large numbers, one

should attempt to recast the problem in a form in which the difference is obtained directly,

possibly through a change of variables. For example, in the above problem, we notice that

n+1

− y

= (e

− 1)e

(6.67)

and we can use a truncated series for the exponential function to obtain

− 1 = h +

+···

= 10

−3

× 10

−6

× 10

−9

= 1.000500167 × 10

−3

Then

n+1

− y

= 1.000500167 × 22.02646579 = 22.03748270

This result is accurate to the full ten digits. The improved accuracy is due to the replacement

of a difference by a product involving a convergent series.

Another example in which roundoff errors can become signiﬁcant occurs in dynamical

problems using Euler angles as generalized coordinates, where these coordinate values are

near a singular point. For type I Euler angles, this singular orientation occurs for the attitude

angle θ near ±π/2. Suppose, for example, that these Euler angles are used in writing the

dynamical equations of a rigid body. A basic physical variable in the rotational dynamics

is the angular velocity component ω

, where

φ −

ψ sin θ (6.68)

For the values of θ near ±π/2, the variables

φ and

ψ may be very large and almost equal,

with ω

a relatively small quantity. Thus, we have the small difference of large quantities

entering the equations of motion, and resulting in signiﬁcant roundoff errors. At the same

time it also may be necessary to use a small step size h in order to keep the truncation

errors under control. Perhaps the best strategy under these conditions is to avoid the use

of Euler angles altogether in the dynamical equations. Another approach such as Euler’s

rotational equations could be used for the dynamics, with the orientation being speciﬁed

340 Introduction to numerical methods

in the kinematical equations by using four Euler parameters, which have no singularity

problems.

Trapezoidal method

Consider the ﬁrst-order equation

y = f (y, t) (6.69)

The trapezoidal integration algorithm is

n+1

= y

n+1

) (6.70)

where

n+1

= f (y

n+1

, t

n+1

) (6.71)

This is an implicit method because y

n+1

appears on both sides of the equation. Usually

this implies that an iterative method of solution must be used. For example, one might start

with a ﬁrst estimate of y

n+1

and use (6.71) to obtain a ﬁrst estimate of

n+1

that is substituted

into (6.70) to obtain a second estimate of y

n+1

. This procedure is repeated until successive

estimates of y

n+1

are sufﬁciently close, assuming that the iterative process converges. These

values are then used as initial data for the next step.

The values of y

n+1

and

n+1

obtained by this iterative process are not, in general, equal

to the true values. Let us use the notation y

∗

n+1

and

∗

n+1

for these computed values, where,

in accordance with the trapezoidal algorithm,

∗

n+1

= y

∗

n+1

) (6.72)

Here, y

and

are assumed to be known. Now let us use a Taylor series to obtain

∗

n+1

≈

n+1

+ h

...

+··· (6.73)

with the result that

∗

n+1

= y

+ h

...

+··· (6.74)

The Taylor series for the true value y

n+1

= y

+ h

...

+··· (6.75)

Hence, the local truncation error is

n+1

= y

n+1

− y

∗

n+1

=−

...

(6.76)

which is of the order h

. The global truncation error is O(h

), so the trapezoidal integration

algorithm is a second-order method.

341 Numerical integration

Modiﬁed Euler method

Now let us combine the two methods we have introduced up to this point. Let us consider

a ﬁrst-order system

y = f (y, t) (6.77)

with y(t

) = y

. The modiﬁed Euler method,orHeun’s method,isatwo-pass method, that

is, the dynamical equation (6.77) is evaluated twice for each step. It consists of the Euler

algorithm as a predictor followed by the trapezoidal algorithm as a corrector for each step.

The method is self-starting because it requires no data for times previous to the nominal

time t

. It is considered to be an explicit method because there are no iterations, even though

the trapezoidal algorithm is used once per step, and we have classed the iterated trapezoidal

algorithm as implicit.

For given y

and t

, the modiﬁed Euler method uses the following procedure

(1)

= f (y

, t

) (6.78)

(2)

n+1

= y

+ h

(6.79)

(3)

n+1

= f (

n+1

, t

n+1

) (6.80)

(4) y

n+1

= y

n+1

) (6.81)

We see that, in (6.79), the Euler method is used to obtain a ﬁrst estimate or predicted value

of y

n+1

, indicated by a tilde (∼). This

n+1

is used in (6.80) to obtain an estimated value of

n+1

, which is then used in the trapezoidal formula of (6.81) to obtain the computed value

n+1

to be used in the following time step. This is the corrected value.

Now let us ﬁnd an expression for the truncation error of the modiﬁed Euler method. We

begin by recalling from (6.64) that the local truncation error due to the use of the Euler

method in calculating

n+1

−

n+1

(6.82)

This error will result in a corresponding error in

n+1

, as compared with the true value

n+1

Assuming small errors, we ﬁnd that

n+1

+ (

n+1

− y

n+1

) f



n+1

(6.83)

where we use the notation f



n+1

= (∂ f /∂y)

n+1

. Then, using (6.81)–(6.83), we obtain the

computed value

∗

n+1

= y

n+1

) −



n+1

(6.84)

By using Taylor expansions for y

n+1

and

n+1

, we ﬁnd that

n+1

) = y

n+1

...

(6.85)

342 Introduction to numerical methods

Finally, we obtain the local truncation error

n+1

= y

n+1

− y

∗

n+1

=−

(

...

− 3 f



) (6.86)

where we have substituted f



for f



n+1

since they differ by O(h).

We notice that, although the order of the local truncation error of the Euler predictor is

O(h

) whereas that of the trapezoidal corrector is O(h

), this apparent mismatch does not

result in a signiﬁcant loss of accuracy. As an example, consider the linear ﬁrst-order system

described by

y = λy (6.87)

where λ is a constant. Then

y = λ

...

= λ

y, etc., and f



= ∂ f /∂y = λ. The local trun-

cation error of the modiﬁed Euler method is

n+1

=−

(

...

− 3 f



) =

(6.88)

If we compare this error with that given by (6.76), we see that this error is twice as large

as the error for the fully iterated and converged trapezoidal method. The global truncation

error of the modiﬁed Euler method is

for this system. Because it is of order h

,it

is classiﬁed as a second-order method.

Runge–Kutta methods

The Runge–Kutta integration algorithms are characterized by being explicit, self-starting,

multiple-pass methods. Consider ﬁrst the second-order Runge–Kutta (RK-2) method. When

applied to the general ﬁrst-order system of (6.77), the RK-2 procedure is as follows:

(1)

= f (y

, t

) (6.89)

(2)

= y

(6.90)

(3)

= f



, t



(6.91)

(4) y

n+1

= y

+ h

(6.92)

Notice that step (2) uses the Euler method to estimate the value of y at t

. This estimate

is substituted into the differential equation to obtain an estimate

of the midpoint

velocity. In step (4), this estimate is used as an approximation of the average velocity in the

calculation of y

n+1

The local truncation error can be shown to be

n+1

(

...

+ 3 f



) (6.93)

For the linear ﬁrst-order system given by (6.87) the local truncation error for RK-2 is

n+1

(6.94)

This is equal to the truncation error for the modiﬁed Euler method.

343 Numerical integration

Now let us consider the widely-used fourth-order Runge–Kutta (RK-4) method.Again

assume a general ﬁrst-order system. The procedure for the RK-4 method is as follows:

(1)

= f (y

, t

) (6.95)

(2)

= y

(6.96)

(3)

= f



, t



(6.97)

(4)

= y

(6.98)

(5)

= f



, t



(6.99)

(6)

n+1

= y

+ h

(6.100)

(7)

n+1

= f (

n+1

, t

n+1

) (6.101)

(8) y

n+1

= y



+ 2

n+1



(6.102)

This is an explicit, self-starting, four-pass method with a global truncation error of O(h

The ﬁrst three steps of the procedure are identical with those of the RK-2 method. Then

two more passes are added in order to improve the accuracy without requiring more initial

data at each time step.

A general analysis of the truncation error of the RK-4 method is rather complicated, but

for the case of a linear system described by

y = λy of (6.87), it can be shown that the local

truncation error is

n+1

= y

n+1

− y

∗

n+1

(λh)

120

(6.103)

Adams–Bashforth predictors

Predictor algorithms are explicit algorithms which can be used individually or can be

coupled with correctors to form an explicit predictor–corrector combination. In general,

Adams–Bashforth (AB) predictors are not self-starting because they use past data which

is not available at the initial time. Hence, some self-starting method such as RK-4 is often

used for the ﬁrst few time steps before switching to the chosen predictor algorithm.

In order to obtain the various Adams–Bashforth predictors, one can ﬁrst recall the deﬁ-

nition of a backward difference, as given by (6.44),

∇y

= y

− y

n−1

(6.104)

Higher-order backward differences are deﬁned by a repeated application of this operator,

with the results given in (6.45)–(6.47). It can be shown that

n+1

= y

+ h



∇

251

720

∇

+···



(6.105)

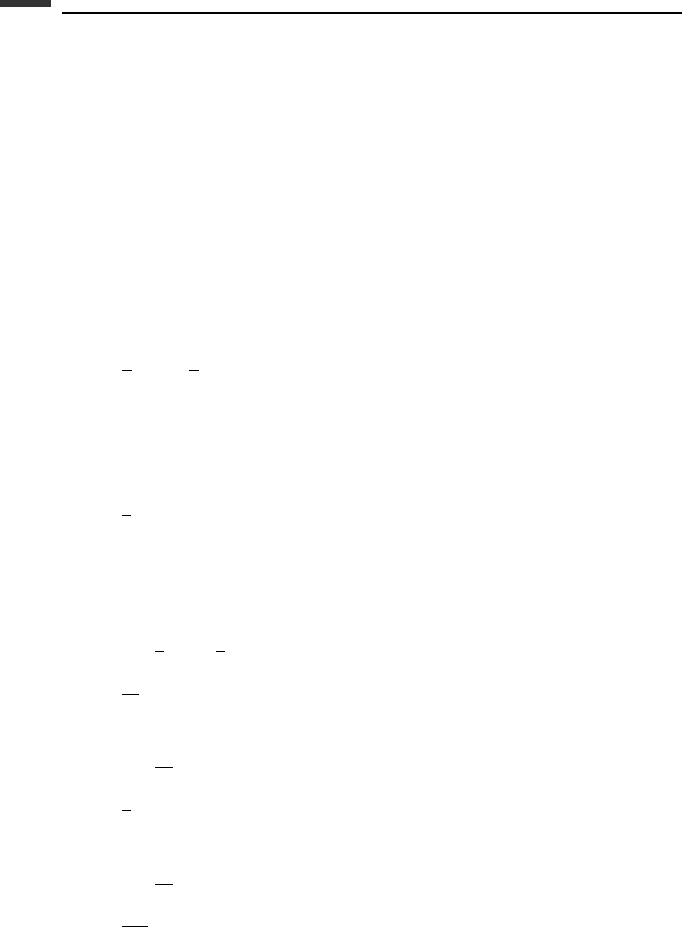
344 Introduction to numerical methods

where

∇

−

n−1

(6.106)

∇

− 2

n−1

n−2

(6.107)

∇

− 3

n−1

+ 3

n−2

−

n−3

(6.108)

∇

− 4

n−1

+ 6

n−2

− 4

n−3

n−4

(6.109)

The various Adams–Bashforth predictors are obtained by truncating the series of (6.105)

at corresponding points. For example, the AB-1 algorithm is identical to the Euler method

and uses only the ﬁrst two terms. Thus, we take

n+1

= y

+ h

(6.110)

and obtain the ﬁrst-order term, or local truncation error, from the next term in (6.105),

namely,

n+1

∇

(

−

n−1

) (6.111)

Now expand

n−1

in a Taylor series about t

and obtain

n−1

− h

+··· (6.112)

Then, from (6.111) and (6.112), we obtain the ﬁrst error term for the AB-1 algorithm.

n+1

(6.113)

In a similar manner, we can obtain other Adams–Bashforth predictor algorithms and the

corresponding ﬁrst error terms. They can be summarized as follows:

AB-2

n+1

= y

−

n−1

(6.114)

n+1

...

(6.115)

AB-3

n+1

= y

(23

− 16

n−1

+ 5

n−2

) (6.116)

n+1

(4)

(6.117)

AB-4

n+1

= y

(55

− 59

n−1

+ 37

n−2

− 9

n−3

) (6.118)

n+1

251

720

(5)

(6.119)

The global truncation errors are equal to E

n+1

/ h in each case. Notice that data from more

steps in the past are required by the higher-order methods.

345 Numerical integration

Adams–Moulton correctors

The Adams–Moulton (AM) algorithms differ from the predictor algorithms by being im-

plicit, that is, variables at time t

n+1

appear on both sides of the integration algorithm. The

derivation of AM algorithms begins with the backward difference expression

n+1

= y

+ h



n+1

−

∇

n+1

−

∇

n+1

−

∇

n+1

−

720

∇

n+1

+···



(6.120)

where

n+1

= f (y

n+1

, t

n+1

) (6.121)

and

∇

n+1

−

(6.122)

∇

n+1

− 2

n−1

(6.123)

∇

n+1

− 3

+ 3

n−1

−

n−2

(6.124)

∇

n+1

− 4

+ 6

n−1

− 4

n−2

n−3

(6.125)

Using procedures similar to those used in deriving the AB algorithms, the following

Adams–Moulton corrector algorithms, and the corresponding ﬁrst error terms, can be ob-

tained.

AM-2 (Trapezoidal)

n+1

= y

(

n+1

) (6.126)

n+1

=−

...

(6.127)

AM-3

n+1

= y

n+1

+ 8

−

n−1

) (6.128)

n+1

=−

(4)

(6.129)

AM-4

n+1

= y

n+1

+ 19

− 5

n−1

n−2

) (6.130)

n+1

=−

720

(5)

(6.131)

The ﬁrst error terms of the AM algorithms are observed to be considerably smaller than

the errors for the corresponding AB algorithms. One reason for the greater accuracy of the

AM algorithms is that they are implicit, and the values of y

n+1

are those which are achieved

after the convergence of the iteration process.

346 Introduction to numerical methods

Truncation errors of predictor–corrector methods

We shall consider Adams–Bashforth predictors followed by Adams–Moulton correctors,

but with only a single pass of the corrector algorithm per step, that is, without iteration.

This leads to truncation errors of the same order in h as the corrector, but generally with a

larger coefﬁcient.

Let us begin with AB-1, AM-2 or the modiﬁed Euler method. This algorithm has been

analyzed previously, and the local truncation error, or ﬁrst error term, is

n+1

=−

(

...

− 3 f



) (6.132)

as in (6.86).

Next consider the AB-2, AM-3 predictor–corrector algorithm. The AB-2 predictor results

in an estimated value of y

n+1

which is

n+1

= y

−

n−1

(6.133)

The ﬁrst error term of this expression is

n+1

−

n+1

= E

n+1

...

(6.134)

Now apply perturbation theory at time t

n+1

to the system differential equation

y = f (y, t) (6.135)

with the result that

n+1

+ ( f



n+1

)(

n+1

− y

n+1

)

n+1

−



...

(6.136)

The AM-3 algorithm gives a computed value

∗

n+1

= y

n+1

+ 8

−

n−1

)

= y

n+1

+ 8

−

n−1

) −

144



...

(6.137)

But from (6.128) and (6.129),

n+1

= y

n+1

+ 8

−

n−1

) −

(4)

(6.138)

Thus, we ﬁnd that the local truncation error for the AB-2, AM-3 predictor–corrector algo-

rithm is

n+1

= y

n+1

− y

∗

n+1

=−

144



(4)

− 25 f



...



(6.139)

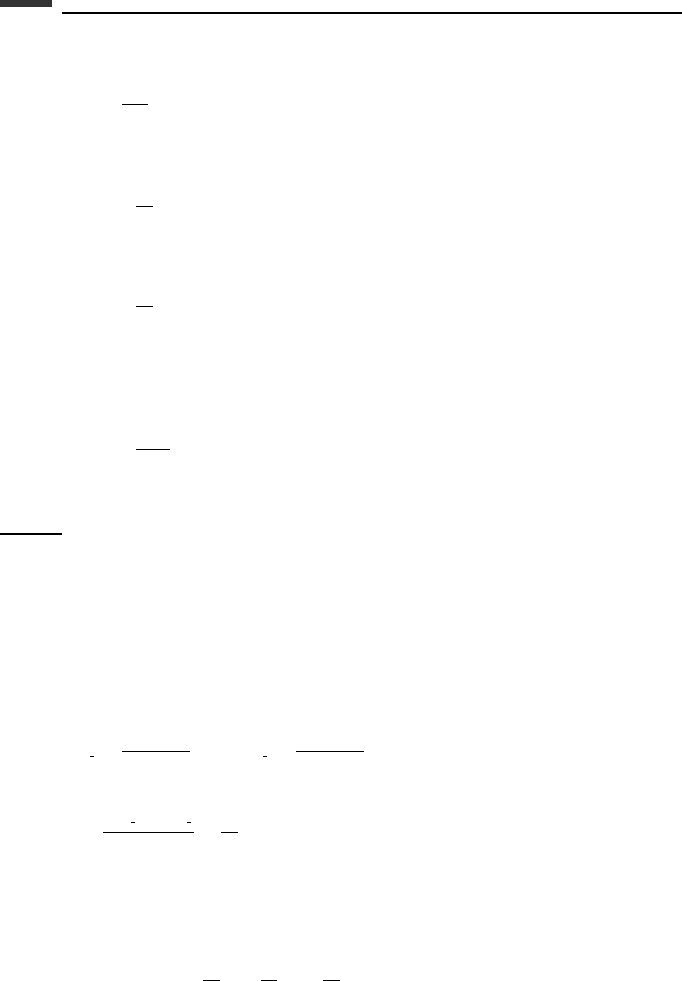
347 Numerical integration

For the particular case of the linear system

y = λy, where λ is a constant, the local truncation

error is

n+1

144

(λh)

(6.140)

If one analyzes the AB-3, AM-3 combination, the truncation error is the same as for the

corrector AM-3 alone, namely,

n+1

=−

(4)

(6.141)

Here, however, no iteration is involved.

For the case of a linear system, this results in

n+1

=−

(λh)

(6.142)

Thus, we ﬁnd that raising the order of the predictor from AB-2 to AB-3 does not change the

order of the truncation error, but it may reduce the magnitude of the numerical coefﬁcient.

Finally, for the AB-3, AM-4 predictor–corrector combination, it can be shown that the

local truncation error is

n+1

=−

2880



70y

(5)

− 405 f



(4)



(6.143)

Special integration algorithms

If the differential equations are of a particular form, it may be possible to use an integration

algorithm which is especially suitable. For example, suppose that the acceleration is not a

function of velocity, that is, it has the form

y = f (y, t) (6.144)

Let us look for an integration algorithm which applies directly to this second-order differ-

ential equation rather than to the equivalent set of two ﬁrst-order equations. Let us begin

with the approximations

≈

n+1

− y

n−

≈

− y

n−1

(6.145)

Then we obtain the basic central difference equation

−

n−

n+1

− 2y

+ y

n−1

) (6.146)

and the following central difference algorithm:

n+1

= 2y

− y

n−1

+ h

(6.147)

A substitution of the Taylor series for y

n−1

results in the computed value

∗

n+1

= y

+ h

...

−

(4)

(6.148)

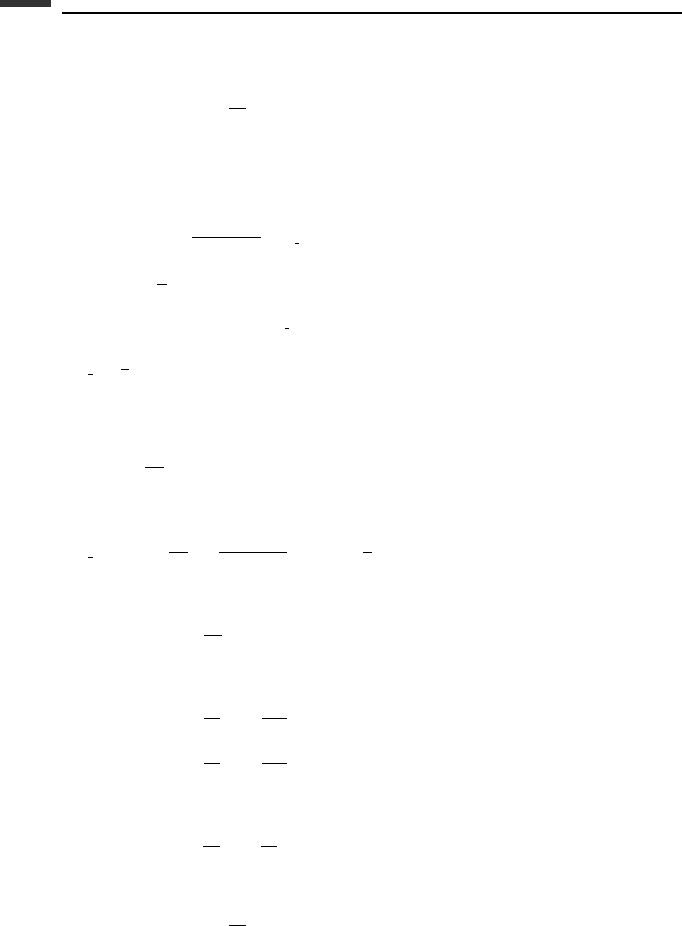
348 Introduction to numerical methods

A comparison of this computed value with the Taylor series for y

n+1

yields the local

truncation error

n+1

= y

n+1

− y

∗

n+1

(4)

(6.149)

The global truncation error is O(h

Next, consider the midpoint method as it applies to the system of (6.144). Let us use the

implicit algorithm

n+1

+ hf



n+1

+ y

, t



(6.150)

n+1

= y

(

n+1

) (6.151)

We see that the acceleration

is obtained by using the midpoint approximation

n+1

+ y

) (6.152)

in (6.144).

Let us use the notation

k(y, t) ≡−

∂ f

∂y

(6.153)

and assume that k is slowly varying over any time step h so k

≈ k

n+1

. Then



∂ f

∂y



n+1

− y



−

n+1

− y

) (6.154)

Thus, (6.150) becomes

n+1

+ h

−

n+1

− y

) (6.155)

A substitution of this expression for

n+1

into (6.151) yields the computed value

∗

n+1

= y

+ h

−

(

n+1

)

= y

+ h

−

+··· (6.156)

where we note that

n+1

≈

. A comparison of this result with the Taylor series

n+1

= y

+ h

...

+··· (6.157)

indicates that the local truncation error is

n+1

= y

n+1

− y

∗

n+1

...

+ 3k

) (6.158)

The midpoint method, also known as the midpoint rule, has the advantages of being

numerically stable and, for certain formulations, can also preserve angular momentum.