Greenwood D.T. Advanced Dynamics
Подождите немного. Документ загружается.


359 Frequency response methods
This results in the numerical value
G
∗
=
1
0.093035 + i0.941412
= 1.057085∠ − 1.472291
We see that the steady-state amplitude of the numerical solution is about one percent too
large. The numerical phase lag is more accurate but is also slightly large.
Example 6.2 Now consider a first-order system which is analyzed using the RK-2 al-
gorithm. We desire the steady-state response to a unit sinusoidal input. The differential
equation is
˙
y = λy + cos ωt (6.234)
In complex form we have
˙
y = λy + e
iωt
(6.235)
The RK-2 algorithm results in
˙
y
n
= λy
n
+ e
iωhn
(6.236)
˜
y
n+
1
2
= y
n
+
1
2
h
˙
y
n
(6.237)
˜
˙
y
n+
1
2
= λ
˜
y
n+
1
2
+ e
iωh
(
n+
1
2
)
(6.238)
y
n+1
= y
n
+ h
˜
˙
y
n+
1
2
=
1 +λh +
(λh)
2
2
y
n
+
λh
2
2
e
iωhn
+ he
iωh
(
n+
1
2
)
(6.239)
The steady-state numerical solution has the form
y
n
= G
∗
(iω)e
iωhn
(6.240)
A substitution of this solution into (6.239) yields the transfer function
G
∗
(iω) =
h
1 +
λh
2
e
−iωh/2
e
iωh/2
−
1 +λh +
(λh)
2
2
e
−iωh/2
(6.241)
or
G
∗
(iω) =
h +
λh
2
2
cos
ωh
2
− i
λh
2
2
sin
ωh
2
−λh
1 +
λh
2
cos
ωh
2
+ i
2 +λh +
(λh)
2
2
sin
ωh
2
(6.242)
The corresponding transfer function for the actual system with continuous time is
G(i ω) =
1
−λ + iω
(6.243)
Note that G
∗
approaches G as the step size h approaches zero.
Let us consider a numerical example with λ =−1, ω = 1 and h = 0.01. With these
values, the RK-2 algorithm yields
G
∗
= 0.707104∠ − 0.785390

360 Introduction to numerical methods
The result for continuous time is
G = 0.707107∠ − 0.785398
We see that the sinusoidal response using RK-2 is slightly small both in amplitude and in
phase lag compared to the true values.
Free sinusoidal response
The effects of truncation errors are most readily apparent in the numerical analysis of
systems having neutral stability. For these systems, any change in damping due to the
integration algorithm appears as a sinusoidal oscillation which is growing or shrinking in
amplitude.
As an illustrative example, consider a linear second-order system described by
¨
y + ω
2
0
y = 0 (6.244)
where ω
0
is the natural frequency in radians per second. If we assume a solution of the form
e
st
, the corresponding characteristic equation is
s
2
+ ω
2
0
= 0 (6.245)
which has the roots
s
1,2
=±iω
0
(6.246)
Case 1
Let us analyze the free unforced response of this system by using the Euler integration
algorithm. First, we write (6.244) in the form of two first-order equations, namely,
˙
y = v (6.247)
˙v =−ω
2
0
y (6.248)
The corresponding difference equations are
y
n+1
= y
n
+ hv
n
(6.249)
v
n+1
= v
n
− hω
2
0
y
n
(6.250)
Assume the solutions
y
n
= Aρ
n
,v
n
= Bρ
n
(6.251)
and substitute into the difference equations. We obtain
(ρ − 1)ρ
n
A − hρ
n
B = 0 (6.252)
hω
2
0
ρ
n
A + (ρ − 1)ρ
n
B = 0 (6.253)

361 Frequency response methods
After dividing these equations by ρ
n
, the characteristic equation that results is obtained
from the determinant of the coefficients, namely,
(ρ − 1)
2
+ h
2
ω
2
0
= 0 (6.254)
with the roots
ρ
1,2
= 1 ± iω
0
h (6.255)
Choose the positive sign in accordance with the usual convention that ρ rotates in the
counterclockwise sense in the complex plane. Use the notation
ρ = Me
iφ
= M∠φ (6.256)
where
M =
1 +ω
2
0
h
2
,φ= tan
−1
(ω
0
h) (6.257)
Since M > 1 for all nonzero values of the step size h, we see that the numerical solution is
unstable for this case of Euler integration.
In general, the numerical solution can be considered to be composed of samples taken
at every time step from a solution of the form e
st
where we now allow the response to be
damped. Thus, the corresponding characteristic equation has the form
s
2
+ 2ζω
n
s + ω
2
n
= 0 (6.258)
with the roots
s
1,2
=−ζω
n
± i ω
n
1 −ζ
2
(6.259)
where ω
n
is the undamped natural frequency and ζ is the damping ratio of the numerical
solution. Now ρ and s are related by the equation
ρ = e
sh
(6.260)
Equivalently, we can write
M = e
−ζω
n
h
(6.261)
φ = ω
n
h
1 −ζ
2
(6.262)
where we assume that 0 ≤ ζ ≤ 1. If ρ is known, that is, if M and φ are given, then ω
n
and
ζ can be obtained from the following equations:
ω
n
=
1
h
ln
2
M +φ
2
(6.263)
ζ =
−ln M
ω
n
h
=
−ln M
ln
2
M +φ
2
(6.264)
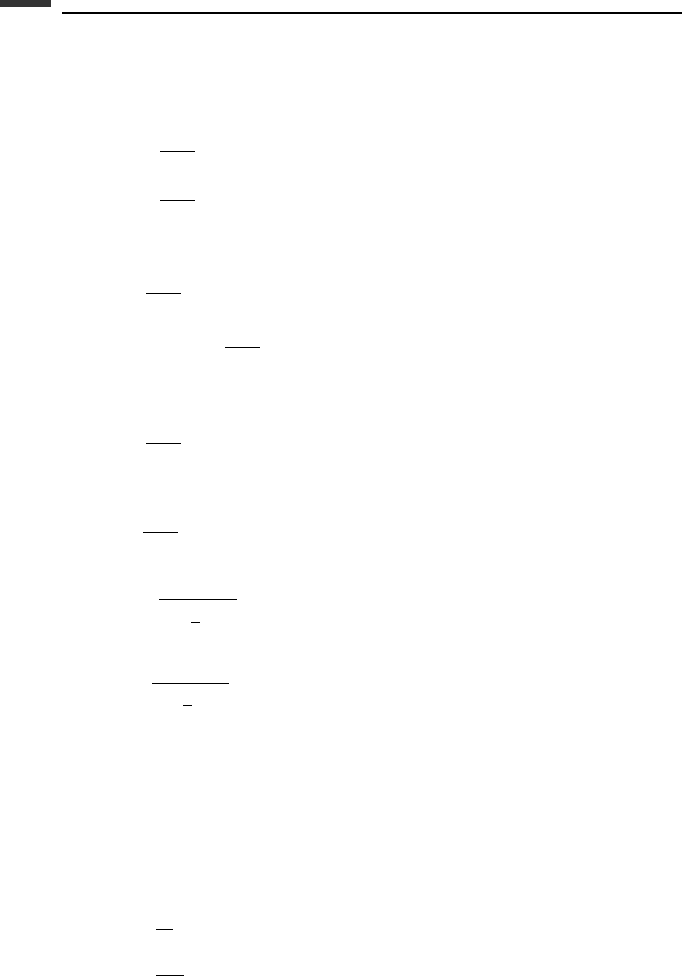
362 Introduction to numerical methods
Case 2
Now let us analyze the same problem using the RK-2 algorithm. The resulting difference
equations are
y
n+1
=
1 −
ω
2
0
h
2
2
y
n
+ hv
n
(6.265)
v
n+1
=
1 −
ω
2
0
h
2
2
v
n
− ω
2
0
hy
n
(6.266)
Again we assume the solution forms of (6.251) and obtain
ρ −
1 −
ω
2
0
h
2
2
ρ
n
A − hρ
n
B = 0 (6.267)
ω
2
0
hρ
n
A +
ρ −
1 −
ω
2
0
h
2
2
ρ
n
B = 0 (6.268)
The resulting characteristic equation is
ρ −
1 −
ω
2
0
h
2
2
2
+ ω
2
0
h
2
= 0 (6.269)
with the roots
ρ
1,2
= 1 −
ω
2
0
h
2
2
± i ω
0
h (6.270)
Thus, we obtain
M =|ρ|=
1 +
1
4
ω
4
0
h
4
(6.271)
φ = tan
−1
ω
0
h
1 −
1
2
ω
2
0
h
2
(6.272)
The values of ω
n
and ζ for the numerical solution are obtained from (6.263) and (6.264).
Since M > 1, the numerical solution is slightly unstable for the usual small values
of ω
0
h.
Case 3
Next, let us use the AB-3 algorithm. In this case, the difference equations are
y
n+1
= y
n
+
h
12
(
23v
n
− 16v
n−1
+ 5v
n−2
)
(6.273)
v
n+1
= v
n
−
ω
2
0
h
12
(23y
n
− 16y
n−1
+ 5y
n−2
) (6.274)
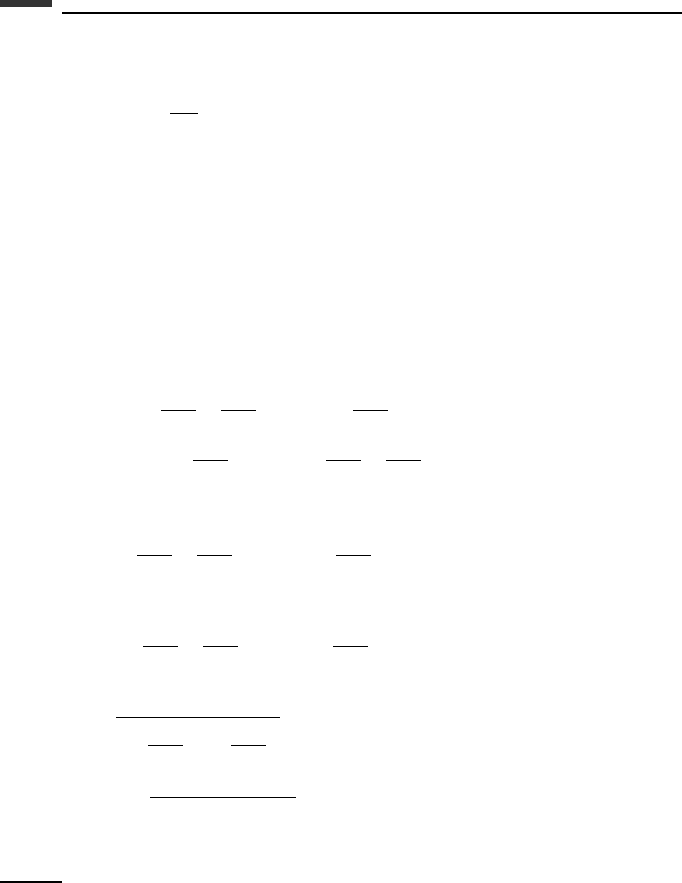
363 Frequency response methods
If we assume the solutions y
n
= Aρ
n
and v
n
= Bρ
n
, we find that the characteristic equation
is
ρ
4
(ρ − 1)
2
+
ω
0
h
12
(23ρ
2
− 16ρ + 5)
2
= 0 (6.275)
This equation has six roots even though the characteristic equation of the actual system
has only two roots. Thus, there are four extraneous roots. These extra roots arise from the
fact that the AB-3 algorithm requires data from two previous steps for each of the two
variables. In the usual case, the four extraneous roots will be stable, and the remaining two
roots will approximate e
sh
for s =±iω
0
.
Case 4
Finally, let us consider the RK-4 algorithm being applied to this problem. The resulting
difference equations are
y
n+1
=
1 −
ω
2
0
h
2
2
+
ω
4
0
h
4
24
y
n
+
1 −
ω
2
0
h
2
6
hv
n
(6.276)
v
n+1
=
−ω
2
0
h +
ω
4
0
h
3
6
y
n
+
1 −
ω
2
0
h
2
2
+
ω
4
0
h
4
24
v
n
(6.277)
The corresponding characteristic equation is
ρ − 1 +
ω
2
0
h
2
2
−
ω
4
0
h
4
24
2
+
ω
0
h −
ω
3
0
h
3
6
2
= 0 (6.278)
and the resulting roots are
ρ
1,2
= 1 −
ω
2
0
h
2
2
+
ω
4
0
h
4
24
± i
ω
0
h −
ω
3
0
h
3
6
(6.279)
In polar form, we obtain
M =
1 −
ω
6
0
h
6
72
1 −
ω
2
0
h
2
8
(6.280)
φ = tan
−1
24ω
0
h − 4ω
3
0
h
3
24 −12ω
2
0
h
2
+ ω
4
0
h
4
(6.281)
Numerical comparisons
In order to obtain a better grasp of the relative accuracies of the various integration algo-
rithms, consider a specific numerical example in which ω
0
= 1 rad/s and h = 0.1s.Inthis
case, the theoretical value of ρ is
ρ = e
i0.1
= 0.995004165 + i0.099833417 (6.282)
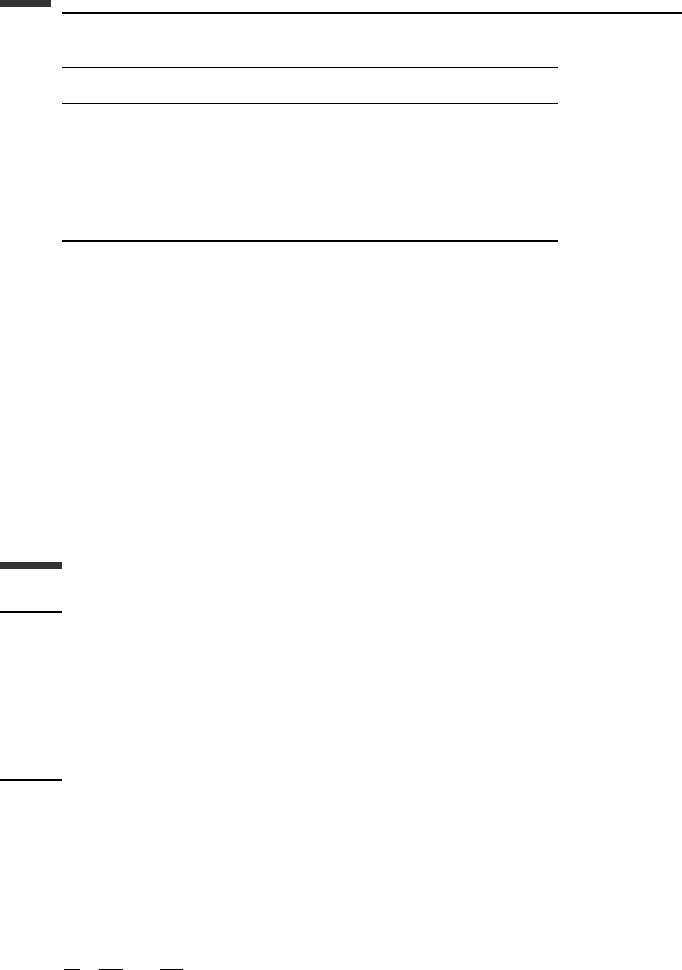
364 Introduction to numerical methods
Table 6.1. A comparison of errors
Method O(h) M − 1 φ −0.1 M(2π )
Euler 1 0.004988 −0.0003313 1.3684
RK-2 2 0.00001250 0.0001662 1.0007844
AB-3 3 −0.00003727 0.000003959 0.997661
RK-4 4 −0.00000000694 −0.00000008304 0.999999566
or
M = 1.0,φ= 0.1 rad (6.283)
The errors in amplitude and phase are shown in Table 6.1. It is interesting to note that
the methods with odd orders of accuracy in h tend to be more accurate in phase, while the
methods of even order in h are relatively more accurate in amplitude. On an absolute basis,
the RK-4 method is quite accurate in both amplitude and phase.
The last column represents the amplitude of the computed solution after one complete
cycle of the oscillation, consisting of approximately 63 time steps. We see that the Euler
solution has increased in amplitude by about 37%, while the amplitude of the RK-4 solution
has an error of less than one part in a million in the analysis of this neutrally stable system.
6.5 Kinematic constraints
An important consideration in the numerical analysis of dynamical systems lies in the proper
representation of kinematical constraints. Even if the physical system is stable, there may
be numerical instabilities resulting from the method of applying constraints. In this section,
we shall present methods of representing constraints and will analyze their stability.
Baumgarte’s method for holonomic constraints
Let us consider first a dynamical system which is subject to m holonomic constraints of the
form
φ
j
(q, t) = 0(j = 1,...,m) (6.284)
Suppose there are n second-order dynamical equations written in the fundamental La-
grangian form
d
dt
∂T
∂
˙
q
i
−
∂T
∂q
i
=
m
j=1
λ
j
a
ji
+ Q
i
(q,
˙
q, t)(i = 1,...,n) (6.285)

365 Kinematic constraints
where the λs are Lagrange multipliers, the Qs are generalized applied forces, and where
a
ji
(q, t) =
∂φ
j
∂q
i
(6.286)
At this point there are n dynamical equations which are linear in the n
¨
qs and the m λs.
We need m additional equations to solve for the variables. These additional equations can
be obtained by differentiating the constraint equations twice with respect to time. First,
˙
φ
j
=
n
i=1
a
ji
(q, t)
˙
q
i
+ a
jt
(q, t) (6.287)
where
a
jt
(q, t) =
∂φ
j
∂t
(6.288)
Then
¨
φ
j
has the form
¨
φ
j
=
n
i=1
a
ji
(q, t)
¨
q
i
+ G
j
(q,
˙
q, t)(j = 1,...,m) (6.289)
If these expressions for
¨
φ
j
are set equal to zero then, with the aid of (6.285), one can
solve for the
¨
q
i
(q,
˙
q, t) and λ
j
(q,
˙
q, t). The n
¨
q
i
expressions can be integrated numerically
for given initial conditions, thereby obtaining
˙
q
i
and q
i
as functions of time.
The problem with this approach is that the resulting numerical solutions will be unstable
even though the physical system may actually be stable. This instability arises from the fact
that, in effect, each constraint equation in the differentiated form
¨
φ
j
= 0(j = 1,...,m) (6.290)
is also being integrated twice with respect to time. This equation has a repeated zero
characteristic root and is therefore unstable.
In order to stabilize the numerical representation of holonomic constraints, Baumgarte
proposed that (6.290) be changed to
¨
φ
j
+ α
˙
φ
j
+ βφ
j
= 0(j = 1,...,m) (6.291)
where α and β are suitably chosen constants whose values may depend on the step size h.
This allows the roots of the corresponding characteristic equation to be shifted to the left
half-plane where the constraint response can be heavily damped.
In detail, the Baumgarte procedure for a system having holonomic constraints is as
follows:
1 Write the differential equations using Lagrange multipliers
d
dt
∂T
∂
˙
q
i
−
∂T
∂q
i
=
m
j=1
λ
j
a
ji
(q, t) + Q
i
(q,
˙
q, t)(i = 1,...,n) (6.292)
2 Solve these n equations for the n
¨
qs
¨
q
i
=
¨
q
i
(q,
˙
q,λ,t)(i = 1,...,n) (6.293)

366 Introduction to numerical methods
3 Define the stabilizing function U
j
U
j
≡−α
˙
φ
j
(q,
˙
q, t) − βφ
j
(q, t)(j = 1,...,m) (6.294)
where
˙
φ
j
is given by (6.287).
4 Stabilize each constraint by setting
¨
φ
j
= U
j
(q,
˙
q, t)(j = 1,...,m) (6.295)
or, using (6.289),
n
i=1
a
ji
(q, t)
¨
q
i
+ G
j
(q,
˙
q, t) = U
j
(q,
˙
q, t)(j = 1,...,m) (6.296)
5 Substitute the
¨
q
i
expressions from (6.293) into (6.296) and solve these m equations for
the m λs
λ
j
= λ
j
(q,
˙
q, t)(j = 1,...,m) (6.297)
6 Substitute from (6.297) back into (6.293), obtaining dynamical equations of the form
¨
q
i
=
¨
q
i
(q,
˙
q, t)(i = 1,...,n) (6.298)
These n second-order equations are integrated numerically, usually by converting them
to 2n first-order equations.
Satisfactory constraint damping can be achieved by setting
α =
2
h
,β=
1
h
2
(6.299)
This corresponds to critical damping of the constraint error φ
j
which may be nonzero. The
constraint errors are driven primarily by truncation errors associated with the numerical
integration algorithm. Hence, they will not disappear entirely, even with the stabilization
procedure.
The numerical stability of a particular constraint function φ(q) can be analyzed by con-
sidering the integration algorithm to be applied directly to the Baumgarte equation
¨
φ + α
˙
φ + βφ = 0 (6.300)
This assumes that the physical system is stable and the step size h is small enough that the
higher-order terms may be neglected in any Taylor expansion.
As a simple example, the Euler integration algorithm results in
φ
n+1
= φ
n
+ h
˙
φ
n
(6.301)
˙
φ
n+1
=
˙
φ
n
+ h
¨
φ
n
= (1 − αh)
˙
φ
n
− βhφ
n
(6.302)
These difference equations have solutions with the forms
φ
n
= Aρ
n
(6.303)
˙
φ
n
= Bρ
n
(6.304)
367 Kinematic constraints
Upon the substitution of these solutions into (6.301) and (6.302), we obtain
(ρ
n+1
− ρ
n
)A − hρ
n
B = 0 (6.305)
βhρ
n
A + (ρ
n+1
− ρ
n
+ αhρ
n
)B = 0 (6.306)
After dividing each equation by ρ
n
and setting the determinant of the coefficients equal to
zero, we obtain the characteristic equation
ρ
2
+ (αh − 2)ρ + (1 − αh + βh
2
) = 0 (6.307)
If we take α proportional to 1/ h and β proportional to 1/h
2
, the roots of the characteristic
equation are independent of the step size. This means that the numerical stability of the
solution for the constraint function φ(q) is also independent of the step size. As an example,
suppose we choose α = 2/ h and β = 1/h
2
. Then the characteristic equation (6.307) has a
double zero root, indicating a “deadbeat” response. This means that, in theory, the constraint
error φ should go to zero in one step, provided that the initial conditions (at n = 0) are
in accordance with the A/B ratio of the corresponding eigenvector. For arbitrary initial
conditions and the given values of α and β, the error will go to zero in two steps, in
theory. In the actual case, however, the constraint error does not go to zero because of new
disturbances at each step due to truncation and roundoff errors.
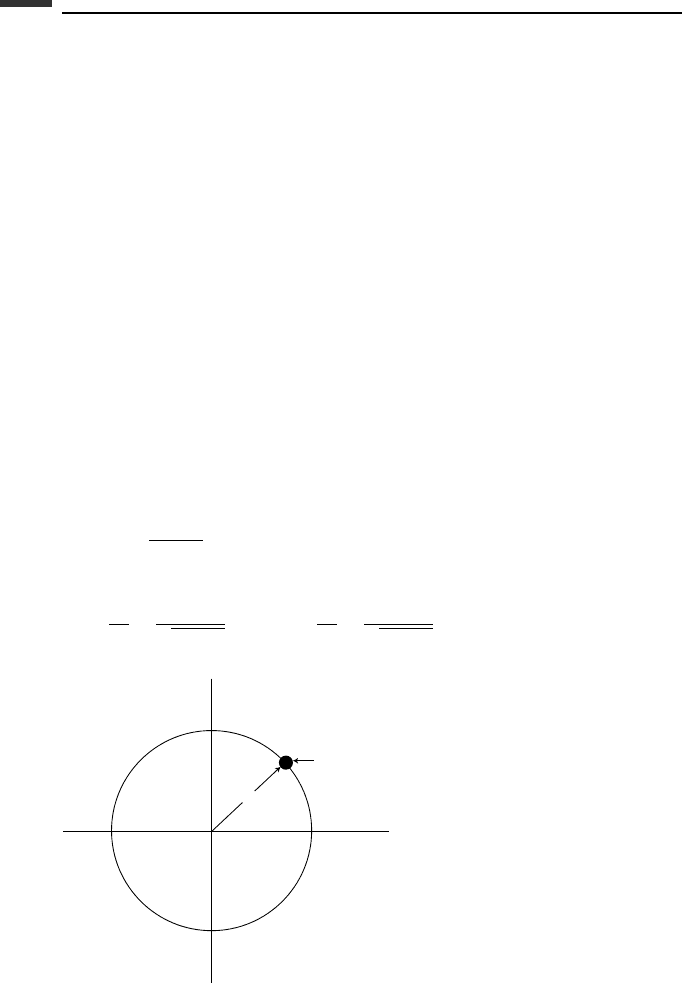
Example 6.3 A particle of mass m moves on a frictionless rigid wire in the form of a
horizontal circle of radius R (Fig. 6.5). The equation of constraint in terms of Cartesian
coordinates is
φ(x, y) =
x
2
+ y
2
− R = 0 (6.308)
Thus, we obtain
a
1x
=
∂φ
∂x
=
x
x
2
+ y
2
, a
1y
=
∂φ
∂y
=
y
x
2
+ y
2
(6.309)
(x, y)
y
x
R
m
Figure 6.5.
368 Introduction to numerical methods
The kinetic energy is
T =
1
2
m(
˙
x
2
+
˙
y
2
) (6.310)
so (6.292) results in the following dynamical equations:
m
¨
x =
λx
x
2
+ y
2
(6.311)
m
¨
y =
λy
x
2
+ y
2
(6.312)
Next, differentiate the constraint function with respect to time,
˙
φ =
1
x
2
+ y
2
(x
˙
x + y
˙
y) (6.313)
A second differentiation with respect to time results in
¨
φ =
1
x
2
+ y
2
x
¨
x + y
¨
y +
˙
x
2
+
˙
y
2
−
1
x
2
+ y
2
(x
˙
x + y
˙
y)
2
= U (6.314)
in accordance with (6.295). In this instance, from (6.294) we have
U =−
α
x
2
+ y
2
(x
˙
x + y
˙
y) −β(
x
2
+ y
2
− R) (6.315)
Now substitute the expressions for
¨
x and
¨
y from (6.311) and (6.312) into (6.314) and solve
for λ/m. We obtain
λ
m
=
−(x
˙
y − y
˙
x)
2
(x
2
+ y
2
)
3/2
+ U (6.316)
Finally, substitute this result back into (6.311) and (6.312) to obtain the following dynamical
equations:
¨
x =
−x (x
˙
y − y
˙
x)
2
(x
2
+ y
2
)
2
+
x
x
2
+ y
2
U (6.317)
¨
y =
−y(x
˙
y − y
˙
x)
2
(x
2
+ y
2
)
2
+
y
x
2
+ y
2
U (6.318)
These equations can be replaced by an equivalent set of four first-order equations, namely,
˙
x = v
x
(6.319)
˙
y = v
y
(6.320)
˙v
x
=−
x
(x
2
+ y
2
)
2
(x v
y
− yv
x
)
2
+
x
x
2
+ y
2
U (6.321)
˙v
y
=−
y
(x
2
+ y
2
)
2
(x v
y
− yv
x
)
2
+
y
x
2
+ y
2
U (6.322)
