Greenwood D.T. Advanced Dynamics
Подождите немного. Документ загружается.

299 Transpositional relations
where
γ
j
rl
=
n
i=1
n
k=1
∂
ji
∂q
k
−
∂
jk
∂q
i
kl
ir
(5.57)
γ
j
r
=
n
i=1
n
k=1
∂
ji
∂q
k
−
∂
jk
∂q
i
kt
ir
+
n
i=1
∂
ji
∂t
−
∂
jt
∂q
i
ir
(5.58)
Then we can express (5.52) in the form
dδq
s
− δdq
s
=−
n
j=1
n
l=1
n
r=1
sj
γ
j
rl
dθ
l
δθ
r
−
n
j=1
n
r=1
sj
γ
j
r
dtδθ
r
+
n
j=1
sj
(dδθ
j
− δdθ
j
)(s = 1,...,n) (5.59)
The basic transpositional equations such as (5.47), (5.54), and (5.59) are written for an
unconstrained system. The application of constraints, however, will be shown to be quite
simple.
Nonholonomic constraints
Consider a system with n generalized coordinates and m nonholonomic constraints which
are linear in the
˙
qs. We can represent these constraints by setting to zero the last m equations
of (5.42) or (5.43). Thus, we have
dθ
j
=
n
i=1
ji
(q, t)dq
i
+
jt
(q, t)dt ( j = 1,...,n − m) (5.60)
dθ
j
=
n
i=1
ji
(q, t)dq
i
+
jt
(q, t)dt = 0(j = n − m +1,...,n) (5.61)
or, in terms of quasi-velocities,
u
j
=
n
i=1
ji
(q, t)
˙
q
i
+
jt
(q, t)(j = 1,...,n − m) (5.62)
u
j
=
n
i=1
ji
(q, t)
˙
q
i
+
jt
(q, t) = 0(j = n − m + 1,...,n) (5.63)
The m constraints are given by (5.63). Note that the first (n − m) us given by (5.62) are
independent. Thus, as velocity variables, we can use the (n − m) us rather than n constrained
˙
qs.
In a similar fashion, using (5.44), we can write the variational equations for the constrained
system.
δθ
j
=
n
i=1
ji
(q, t)δq
i
( j = 1,...,n − m) (5.64)
δθ
j
=
n
i=1
ji
(q, t)δq
i
= 0(j = n − m + 1,...,n) (5.65)

300 Equations of motion: integral approach
The m virtual or instantaneous constraint equations are given by (5.65).
With the application of the constraints, we see that
dδθ
j
= 0,δdθ
j
= 0(j = n − m + 1,...,n) (5.66)
so (5.49) becomes
dδθ
j
− δdθ
j
= F
j
+
n
i=1
ji
(dδq
i
− δdq
i
)(j = 1,...,n − m) (5.67)
and (5.52) reduces to
dδq
r
− δdq
r
=−
n
i=1
ri
F
i
+
n−m
j=1
rj
(dδθ
j
− δdθ
j
)(r = 1,...,n) (5.68)
The theorem of Frobenius
If the expressions for F
j
given in (5.48) are all equal to zero for an unconstrained system,
then the exactness conditions apply for the n differential forms of (5.42). These exactness
conditions are sufficient for the integrability of the differential forms, implying that the θ s
are true generalized coordinates rather than quasi-coordinates.
A question arises concerning the necessary and sufficient conditions for the integrabil-
ity of the differential forms if there are constraints. This is answered by the Theorem of
Frobenius: A system of differential equations such as (5.42) is completely integrable to
yield θ
j
= θ
j
(q, t) for j = 1,...,n if and only if F
j
= 0 for all dq
i
and δq
i
satisfying the
constraints. Recall that F
j
is given by (5.48).
As an example, consider a constraint which is represented by the differential form
dθ = a(x, y, z)dx + b(x, y, z)dy + c(x, y, z)dz = 0 (5.69)
Also,
δθ = a(x, y, z)δx + b(x , y, z)δy + c(x, y, z)δz = 0 (5.70)
This constraint is integrable, that is, holonomic if F
j
= 0 or, in detail, if
∂a
∂y
−
∂b
∂x
(dyδx − dxδy) +
∂b
∂z
−
∂c
∂y
(dzδy − dyδz)
+
∂c
∂x
−
∂a
∂z
(dxδz − dzδx) = 0 (5.71)
where, from (5.69) and (5.70),
dz =−
1
c
(adx + bdy),δz =−
1
c
(aδx + bδy) (5.72)
Upon making these substitutions and simplifying, we obtain
∂a
∂y
−
∂b
∂x
+
a
c
∂b
∂z
−
∂c
∂y
+
b
c
∂c
∂x
−
∂a
∂z
(dyδx − dxδy) = 0 (5.73)

301 Transpositional relations
where dx, δx, dy, δy are independent. Hence, we find that
a
∂b
∂z
−
∂c
∂y
+ b
∂c
∂x
−
∂a
∂z
+ c
∂a
∂y
−
∂b
∂x
= 0 (5.74)
This is the necessary and sufficient condition for the integrability of (5.69).
Geometrical considerations
First, let us consider an unconstrained system described in terms of n quasi-velocities which
are given by (5.43). We wish to compare points on an actual path in n-dimensional q-space
with the corresponding points on a varied path. This can be visualized by considering a
small quadrilateral ABCD, as shown in Fig. 5.3a. The infinitesimal vector dq occurs on
the actual path during a small time interval dt. The variation δq is an infinitesimal vector
drawn from a point on the actual path to a corresponding point (at the same time) on the
varied path. Thus, the operator d refers to differences that occur along a solution path with
the passage of time; whereas, δ refers to differences in going from the actual path to a varied
path with time held constant.
For this unconstrained case, the small quadrilateral ABCD is closed. We see that the
vector displacements ABC and ADC are equal. Thus
dq + δq + dδq = δq + dq + δdq (5.75)
and
dδq = δdq (5.76)
In terms of components,
dδq
i
− δdq
i
= 0(i = 1,...,n) (5.77)
This result applies to a holonomic system for which all F
j
= 0. On the other hand, even for
an unconstrained or holonomic system, if (5.77) applies, then (5.49) shows that for each
F
j
= 0 due to the presence of quasi-velocities, there is a corresponding transpositional term
dδθ
j
− δdθ
j
= 0 (5.78)
A
B
D
C
actual
path
varied
path
dq+δdq
δq
dq
δq+ dδq
(a)
A
B
C
D
C'
actual
path
dq+δdq
δq
dq
δq+dδq
(b)
Figure 5.3.

302 Equations of motion: integral approach
Now let us consider the more general case in which there are m nonholonomic constraints
that are applied to the system by setting the last m differential forms equal to zero. Thus,
we assume that
dθ
j
= 0,δθ
j
= 0(j = n − m + 1,...,n) (5.79)
as in (5.61) and (5.65). Since the virtual constraint applies at B and the actual constraint
applies at D in Fig. 5.3b, we see that
dδθ
j
= 0,δdθ
j
= 0(j = n − m + 1,...,n) (5.80)
and therefore
dδθ
j
− δdθ
j
= 0(j = n − m + 1,...,n) (5.81)
Assuming that F
j
= 0for j = n − m +1,...,n, we see from (5.49) that at least m of
the dδq
i
− δdq
i
are nonzero, implying that
dδq − δdq = 0 (5.82)
Thus, the quadrilateral in Fig. 5.3b does not close, and the vector in n-space directed from
C
to C is equal to dδq − δdq. This lack of closure indicates that, even at the differential
level, there is path dependence due to the nonintegrability of the nonholonomic constraints.
For example, if there is one nonholonomic constraint, it is kinematically possible to obtain
closure for all but one of the component qs. However, the remaining dδq
i
− δdq
i
must
be nonzero, resulting in nonclosure in n-space. Similarly, if there are m nonholonomic
constraints, then at least m of the dδq
i
− δdq
i
must be nonzero.
For a nominal point A on the actual path, it is important to understand how the
ji
(q, t)
and
jt
(q, t) coefficients are evaluated when applying the constraints at points B and D.
At A we have the constraint equations
n
i=1
ji
dq
i
+
jt
dt = 0(j = n − m +1,...,n) (5.83)
n
i=1
ji
δq
i
= 0(j = n − m + 1,...,n) (5.84)
where the
ji
and
jt
coefficients are evaluated at A.AtB we have
(
ji
)
B
=
ji
+
n
k=1
∂
ji
∂q
k
dq
k
+
∂
ji
∂t
dt (5.85)
where the terms on the right are again evaluated at A. Thus, for the virtual constraint at B,
we obtain
n
i=1
ji
+
n
k=1
∂
ji
∂q
k
dq
k
+
∂
ji
∂t
dt
(δq
i
+ dδq
i
) = 0 (5.86)

303 Transpositional relations
and, keeping terms to second order, there remains
n
i=1
ji
δq
i
+
n
i=1
ji
dδq
i
+
n
i=1
n
k=1
∂
ji
∂q
k
dq
k
δq
i
+
n
i=1
∂
ji
∂t
dtδq
i
= 0
( j = n − m +1,...,n) (5.87)
Similarly, at D the coefficients are
(
jk
)
D
=
jk
+
n
i=1
∂
jk
∂q
i
δq
i
(5.88)
(
jt
)
D
=
jt
+
n
i=1
∂
jt
∂q
i
δq
i
(5.89)
Hence, the actual constraint equation at D requires that
n
k=1
jk
+
n
i=1
∂
jk
∂q
i
δq
i
(dq
k
+ δdq
k
) +
jt
+
n
i=1
∂
jt
∂q
i
δq
i
dt = 0 (5.90)
and, omitting third-order terms, we obtain
n
k=1
jk
dq
k
+
n
k=1
jk
δdq
k
+
n
i=1
n
k=1
∂
jk
∂q
i
dq
k
δq
i
+
jt
dt +
n
i=1
∂
jt
∂q
i
dtδq
i
= 0
( j = n − m +1,...,n) (5.91)
Now subtract (5.91) from (5.87) and recall the constraint equations at A, namely, (5.83)
and (5.84). The result is
n
i=1
ji
(dδq
i
− δdq
i
) +
n
i=1
n
k=1
∂
ji
∂q
k
−
∂
jk
∂q
i
dq
k
δq
i
+
n
i=1
∂
ji
∂t
−
∂
jt
∂q
i
dtδq
i
= 0(j = n − m + 1,...,n) (5.92)
This is identical to the basic equation (5.47) for the case of m nonholonomic constraints
with
dδθ
j
− δdθ
j
= 0(j = n − m + 1,...,n) (5.93)
We have presented a derivation which emphasizes the assumptions concerning the values
of the coefficients at points B and D which are slightly displaced from the nominal reference
point A. Note, however, that ultimately all calculations involve values at A; and this applies
as well to calculations of F
j
.
As a result of the lack of closure of the differential quadrilaterals if there are nonholonomic
constraints, it is not possible to find a continuous varied path which simultaneously satisfies
the actual constraints and the virtual or instantaneous constraints. One must choose one or
the other. If one chooses the stationarity principle in which the varied paths are required
to satisfy the actual constraints but not the virtual constraints, then incorrect equations of
304 Equations of motion: integral approach
motion result, as we found earlier. On the other hand, if the varied paths satisfy the virtual
constraints but not the actual constraints, the variational process produces correct equations
of motion, as we found in the discussion of Hamilton’s principle.
5.3 The Boltzmann–Hamel equation, transpositional form
Derivation
The general form of the Boltzmann–Hamel equation, as given in (4.85), is
d
dt
∂T
∂u
r
−
∂T
∂θ
r
+
n
j=1
n−m
l=1
∂T
∂u
j
γ
j
rl
u
l
+
n
j=1
∂T
∂u
j
γ
j
r
= Q
r
(r = 1,...,n − m)
(5.94)
where T (q, u, t )istheunconstrained kinetic energy and Q
r
is the generalized applied
force associated with u
r
. The (n − m) us are independent and u
r
=
˙
θ
r
where θ
r
is a quasi-
coordinate.
Multiply (5.94) by δθ
r
dt and sum over r. We obtain
n−m
r=1
d
dt
∂T
∂u
r
−
∂T
∂θ
r
− Q
r
δθ
r
dt
+
n
j=1
n−m
r=1
n−m
l=1
∂T
∂u
j
γ
j
rl
dθ
l
δθ
r
+
∂T
∂u
j
γ
j
r
dtδθ
r
= 0 (5.95)
Now recall that with the application of the m constraints,
dθ
l
= 0,δθ
l
= 0(l = n − m + 1,...,n) (5.96)
and thus, from (5.56),
F
j
=
n−m
l=1
n−m
r=1
γ
j
rl
dθ
l
δθ
r
+
n−m
r=1
γ
j
r
dtδθ
r
( j = 1,...,n) (5.97)
Hence, we find that
n−m
r=1
d
dt
∂T
∂u
r
−
∂T
∂θ
r
− Q
r
δθ
r
dt +
n
j=1
∂T
∂u
j
F
j
= 0 (5.98)
Let us assume that
dδθ
j
− δdθ
j
= 0(j = 1,...,n − m) (5.99)
so that this transpositional expression is now equal to zero for all j . Then, from (5.49), we
obtain
F
j
=−
n
i=1
ji
(dδq
i
− δdq
i
) (5.100)
305 The Boltzmann–Hamel equation, transpositional form
Finally, dividing by dt, we can write (5.98) in the form
n−m
r=1
d
dt
∂T
∂u
r
−
∂T
∂θ
r
− Q
r
δθ
r
−
n
i=1
n
j=1
∂T
∂u
j
ji
d
dt
(δq
i
) −δ
˙
q
i
= 0 (5.101)
This is the transpositional form of the Boltzmann–Hamel equation. The (n − m) equations
of motion are obtained by writing the transpositional expressions in terms of the δθs and
then setting the coefficient of each δθ
r
equal to zero. This approach results in the same
equations of motion as (5.94) but is somewhat simpler to apply.
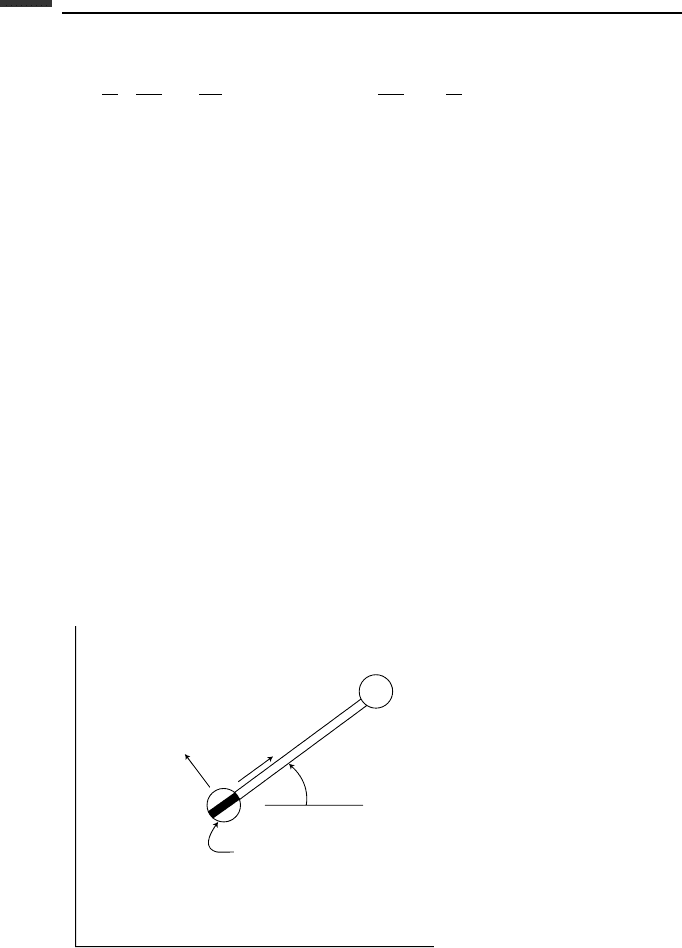
Example 5.2 A dumbbell consists of two particles, each of mass m, connected by a
massless rod of length l. There is a knife-edge constraint at particle 1 (Fig. 5.4). We wish
to find the equations of motion as the system moves in the horizontal xy-plane.
Let us use (5.101). The generalized coordinates are (x, y,φ) and the usare
u
1
= v =
˙
x cos φ +
˙
y sin φ
u
2
=
˙
φ
u
3
= w =−
˙
x sin φ +
˙
y cos φ = 0
(5.102)
where the last equation is the nonholonomic constraint equation. The coefficient matrix is
=
cos φ sin φ 0
001
−sin φ cos φ 0
(5.103)
As quasi-coordinates, let us choose s and η, where
˙
s = v and ˙η = w. The angle φ is a
true coordinate.
y
x
w
m
l
v
m
(x, y)
1
2
φ
Figure 5.4.

306 Equations of motion: integral approach
In evaluating the transpositional terms we note that, for the unconstrained system,
˙
x = v cos φ − w sin φ (5.104)
˙
y = v sin φ + w cos φ (5.105)
so
δx = cos φδs − sin φδη (5.106)
δy = sin φδs + cos φδη (5.107)
From (5.99), we see that
d
dt
(δs) = δv,
d
dt
(δφ) = δ
˙
φ,
d
dt
(δη) = δw (5.108)
Then
d
dt
(δx ) = cos φδv−
˙
φ sin φδs − sin φδw−
˙
φ cos φδη (5.109)
δ
˙
x = cos φδv− v sin φδφ− sin φδw− w cos φδφ (5.110)
Now apply the actual and virtual constraint equations resulting in
w = 0,δw= 0,δη= 0 (5.111)
and we obtain
d
dt
(δx ) − δ
˙
x = sin φ(vδφ −
˙
φδs) (5.112)
In a similar manner, we find that
d
dt
(δy) = sin φδv+
˙
φ cos φδs (5.113)
δ
˙
y = sin φδv+ v cos φδφ (5.114)
and thus
d
dt
(δy) − δ
˙
y = cos φ(
˙
φδs − vδφ) (5.115)
Notice from (5.108) that
d
dt
(δφ) −δ
˙
φ = 0 (5.116)
Then, with the aid of (5.103), we find that
n
i=1
ji
d
dt
(δq
i
) −δ
˙
q
i
= 0 (5.117)
for j = 1 and j = 2. For j = 3, we obtain
n
i=1
ji
d
dt
(δq
i
) −δ
˙
q
i
= (sin
2
φ + cos
2
φ)(
˙
φδs − vδφ)
=
˙
φδs − vδφ (5.118)
307 The central equation
The unconstrained kinetic energy is
T = m(v
2
+ w
2
) +
1
2
ml
2
˙
φ
2
+ ml
˙
φw (5.119)
Furthermore, all the Qs are equal to zero. Now we can substitute into the general equation
(5.101), resulting in
2m ˙vδs + ml
2
¨
φδφ − ml
˙
φ(
˙
φδs − vδφ) = 0 (5.120)
The v equation of motion, obtained by setting the coefficient of δs equal to zero, is
2m ˙v − ml
˙
φ
2
= 0 (5.121)
Similarly, the coefficient of δφ is
ml
2
¨
φ + mlv
˙
φ = 0 (5.122)
yielding the second equation of motion. A comparison shows that this approach is somewhat
less complicated than the usual Boltzmann–Hamel method.
5.4 The central equation
Derivation
Consider a system of N particles. Let us begin with d’Alembert’s principle in the form
N
i=1
(F
i
− m
i
¨
r
i
) ·δr
i
= 0 (5.123)
where r
i
is the position vector of the i th particle and F
i
is the applied force acting on it.
The virtual displacements δr
i
satisfy the instantaneous (virtual) constraints.
We can write the kinematic identity
d
dt
(v
i
· δr
i
) =
¨
r
i
· δr
i
+ v
i
·
d
dt
(δr
i
)
=
¨
r
i
· δr
i
+ δ
v
i
· v
i
2
+ v
i
·
d
dt
(δr
i
) −δv
i
(5.124)
where the particle velocity v
i
=
˙
r
i
.Nowlet
δ P =
N
i=1
m
i
v
i
· δr
i
(5.125)
δT =
N
i=1
m
i
δ
v
i
· v
i
2
(5.126)
δ D =
N
i=1
m
i
v
i
·
d
dt
(δr
i
) −δv
i
(5.127)
δW =
N
i=1
F
i
· δr
i
(5.128)

308 Equations of motion: integral approach
From (5.123)–(5.128), we obtain the central equation of Heun and Hamel:
d
dt
(δ P) = δT + δW + δ D (5.129)
Explicit form
The central equation has the same general validity as d’Alembert’s principle from which it
was derived. The principal assumption is that the δrs satisfy the virtual constraints. There
is a need, however, to put the central equation in a more convenient, usable form.
First, let us transform to generalized coordinates. In terms of velocity coefficients, we
have
v
i
=
n
k=1
γ
ik
(q, t)
˙
q
k
+ γ
it
(q, t)(i = 1,...,N ) (5.130)
δr
i
=
n
k=1
γ
ik
(q, t) δq
k
(i = 1,...,N) (5.131)
Thus, we find that
d
dt
(δr
i
) =
n
k=1
γ
ik
d
dt
(δq
k
) +
n
k=1
n
l=1
∂γ
il
∂q
k
˙
q
k
δq
l
+
n
l=1
∂γ
il
∂t
δq
l
(5.132)
and
δv
i
=
n
k=1
γ
ik
δ
˙
q
k
+
n
k=1
n
l=1
∂γ
ik
∂q
l
˙
q
k
δq
l
+
n
l=1
∂γ
it
∂q
l
δq
l
(5.133)
But
γ
ik
=
∂v
i
∂
˙
q
k
=
∂r
i
∂q
k
, γ
it
=
∂r
i
∂t
(5.134)
so we obtain
∂γ
il
∂q
k
=
∂
2
r
i
∂q
k
∂q
l
=
∂γ
ik
∂q
l
,
∂γ
il
∂t
=
∂
2
r
i
∂t∂q
l
=
∂γ
it
∂q
l
(5.135)
for i = 1,...,N and k, l = 1,...,n. Thus, from (5.132)–(5.135), we find that
d
dt
(δr
i
) −δv
i
=
n
k=1
γ
ik
d
dt
(δq
k
) −δ
˙
q
k
(5.136)
The kinetic energy is
T =
1
2
N
i=1
m
i
v
i
· v
i
(5.137)
