Greenwood D.T. Advanced Dynamics

Подождите немного. Документ загружается.

269 Constraints and energy rates

where



i=1



k=1



∂

∂q

−

∂

∂q







i=1



∂

∂t

−

∂

∂q





(4.395)

It appears that, in the general nonholonomic case, the left-hand side of (4.394) is easier to

evaluate that is its right-hand side. Thus, (4.380) is more direct than (4.393) in the general

case.

From (4.380), we see that sufﬁcient conditions for a conservative system, implying a

constant value of E,are:

1. Q



= 0 for all j, that is, all the generalized forces Q

are derivable from a potential

energy function of the form V (q).

2. The functions 

, p

· ˙γ

, and H

are all continuously equal to zero.

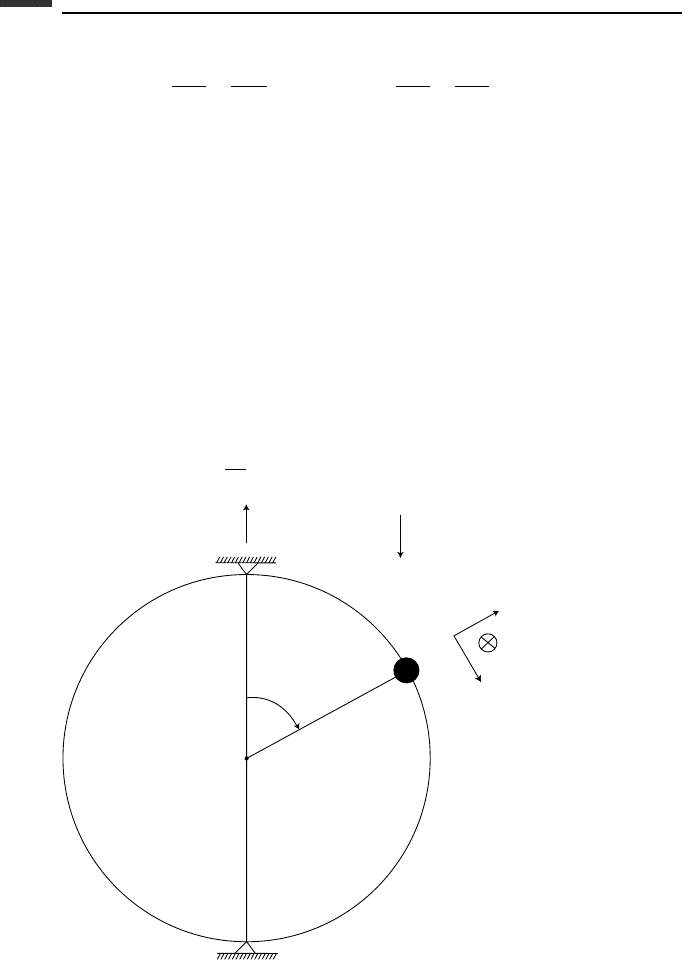
Example 4.12 A particle of mass m can slide on a wire in the form of a circle of radius r

which rotates about a vertical diameter with a variable angular velocity (t) (Fig. 4.8). We

wish to determine the energy rate

This is a rheonomic holonomic system with one generalized coordinate and no constraints.

Lagrange’s equation applies and (4.355) reduces to

E =

−

V =−

∂ L

∂t

(4.396)

Ω (t)

Figure 4.8.

270 Equations of motion: differential approach

We see that

T =

(

+ 

sin

θ) (4.397)

V = mgr cos θ (4.398)

Thus, we obtain

E =−

∂T

∂t

=−mr



 sin

θ (4.399)

For the particular case in which  is constant, we see that E = T

− T

+ V has a constant

value and the system is conservative. The total energy T + V is not constant, however,

because there is a torque about the vertical axis that is required to keep the angular velocity

 constant even though θ is varying.

If we use the Boltzmann–Hamel approach, as given in (4.393), the same result occurs.

Here we can take u

θ and note that both 

and γ

vanish.

Finally, if we use the general energy rate expression in (4.379), we ﬁnd that it reduces to

E =−mv

· ˙γ

(4.400)

where

= r

θe

+r sin θ e

(4.401)

= r  sin θ e

(4.402)

Now

= Ω × e

=− sin θ e

−  cos θ e

(4.403)

˙γ

=−r

sin

θ e

−r

sin θ cos θ e

+r(

 sin θ + 

θ cos θ )e

(4.404)

Thus, (4.400) results in

E =−mr



 sin

θ (4.405)

in agreement with our earlier results.

One can check the energy rate by ﬁrst noting that

= mr

θ (4.406)

= mr



θ sin θ cos θ + mr



 sin

θ (4.407)

V =−mgr

θ sin θ (4.408)

The equation of motion, obtained from Lagrange’s equation, is

θ − mr



sin θ cos θ − mgr sin θ = 0 (4.409)

Substitute the expression for mr

θ from (4.409) into (4.406). Then we ﬁnd that

E =

−

V =−mr



 sin

θ (4.410)

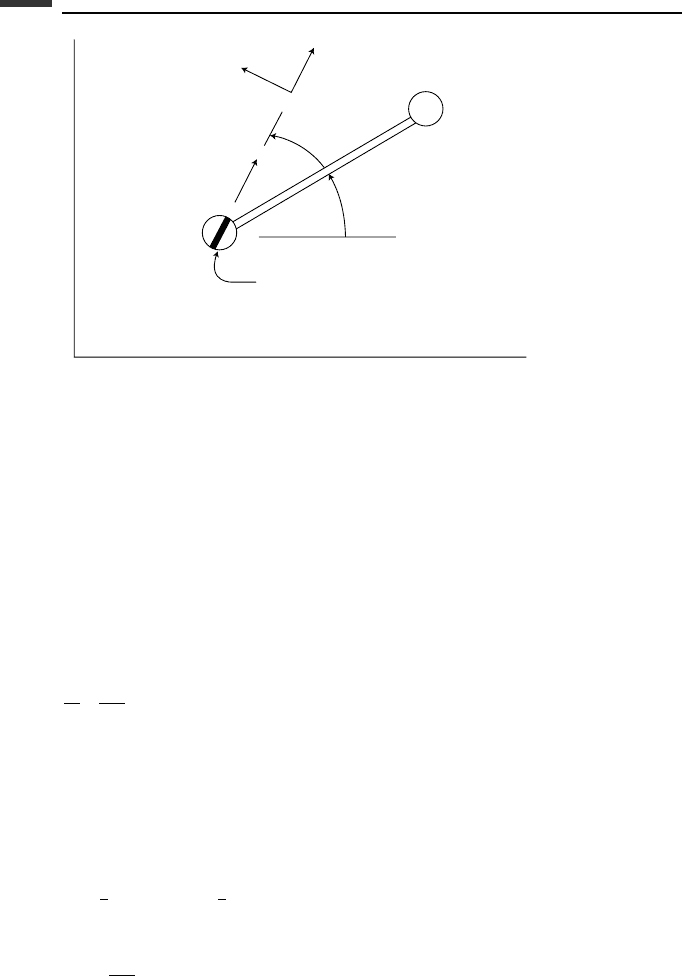
271 Constraints and energy rates

(x, y)

Ωt

Figure 4.9.

which checks with (4.405).

Example 4.13 A rheonomic nonholonomic system consists of two particles, each of mass

m which are connected by a massless rod of length l, as shown in Fig. 4.9. Particle 1 has

a nonholonomic constraint in the form of a knife-edge which rotates at a constant rate 

relative to the rod. Let us choose (x , y,φ)asqs, and let

= v, u

φ (4.411)

where v is a quasi-velocity. We wish to ﬁnd the differential equations of motion and to

evaluate the energy rate

First, the differential equations of motion are obtained from the fundamental equation

for a system of particles, namely,



∂T

∂u



−



i=1

· ˙γ

= Q

(4.412)

Assume that the xy-plane is horizontal. The only constraint force is perpendicular to the knife

edge and does no work in an arbitrary virtual displacement. Therefore, each generalized

applied force Q

is zero. The velocities of the two particles are

= ve

, v

= (v + l

φ sin t)e

φ cos t e

(4.413)

Thus, the constrained kinetic energy is

T =



+ v



m(2v

+ 2lv

φ sin t) (4.414)

The velocity coefﬁcients are

∂v

∂u

(4.415)

272 Equations of motion: differential approach

resulting in

= e

, γ

= 0, γ

= e

, γ

= l(sin t e

+ cos t e

) (4.416)

Also, we note that the γ

coefﬁcients are equal to zero.

A differentiation of (4.416) with respect to time results in

˙γ

= 0, ˙γ

= ˙γ

= (

φ + )e

, ˙γ

= l

φ(−cos t e

+ sin t e

) (4.417)

where we note that e

and e

rotate counterclockwise with an angular velocity (

φ + ).

The u

equation is obtained by ﬁrst evaluating



∂T

∂v



= 2m ˙v + ml

φ sin t + ml

φ cos t (4.418)

In addition, we ﬁnd that

m(v

· ˙γ

+ v

· ˙γ

) = ml

φ(

φ + ) cos t (4.419)

Then, using (4.412), the ﬁrst equation of motion is

2m ˙v + ml

φ sin t − ml

cos t = 0 (4.420)

In a similar manner, we obtain



∂T

∂



= ml

φ + ml ˙v sin t + mlv cos t

(4.421)

m(v

· ˙γ

+ v

· ˙γ

) =−mlv

φ cos t (4.422)

The second equation of motion is

φ + ml ˙v sin t + mlv(

φ + ) cos t = 0 (4.423)

These two equations of motion constitute a minimum set for this system which has two

degrees of freedom.

Equation (4.420) can be interpreted as stating that the rate of change of linear momentum

in the direction of the knife edge is equal to zero. The second equation of motion, (4.423),

states that, if particle 1 is chosen as a noninertial reference point, the rate of change of

angular momentum is equal to the inertial moment due to the acceleration of particle 1.

Thus, it is convenient to think in terms of an accelerating but nonrotating reference frame

in this instance.

The energy rate

E for a system of N particles can be written in the form

E =

n−m



r=1



∂V

∂t



k=1

∂V

∂q



−



i=1

· ˙γ

(4.424)

in accordance with (4.379). We ﬁnd that Q



, V , 

and γ

are all equal to zero, so

E = 0.

Thus, the energy function E, which in this case is the total kinetic energy, is constant during

the motion.

This is an example of a system for which the kinetic energy is an explicit function of

time and yet it is conservative.

273 Constraints and energy rates

Second method If the Lagrangian method is used, we have three differential equations

of motion involving Lagrange multipliers. Also, there is the nonholonomic constraint

equation

−

x sin(φ + t) +

y cos(φ + t ) = 0 (4.425)

which states that the velocity of particle 1 normal to the knife edge is zero.

The kinetic energy of the unconstrained system is

T =

m[2

+ 2

+ 2l

φ(−

x sin φ +

y cos φ)] (4.426)

We note that T is not an explicit function of time, and we can take the potential energy

function V equal to zero; hence ∂ L/∂t = 0. Furthermore, the nonholonomic constraint

is homogeneous and linear in the

qs, and is therefore conservative. Thus, the sufﬁcient

conditions for a conservative system are satisﬁed, implying, in this case, that the total

kinetic energy is a constant of the motion.

Third method Let us use the Boltzmann–Hamel approach. The equations for a complete

setofthreeus in terms of

qsare

= v =

x cos(φ + t) +

y sin(φ + t) (4.427)

φ (4.428)

=−

x sin(φ + t) +

y cos(φ + t ) (4.429)

The nonholonomic constraint is applied by setting u

equal to zero.

The unconstrained kinetic energy is

T = m



+ u

+lu

sin t +u

cos t)



(4.430)

and the general Boltzmann–Hamel equation (4.85) reduces to



∂T

∂u





j=1



l=1

∂T

∂u



j=1

∂T

∂u

= 0(r = 1, 2) (4.431)

In evaluating γ

and γ

, we note that the 

coefﬁcients are explicit functions of time, in

general, but all the 

coefﬁcients vanish, as well as the 

After a rather lengthy calculation, the equations of motion found earlier in (4.420) and

(4.423) are obtained. The Boltzmann–Hamel energy rate expression in (4.393) reduces for

this example to

E =−

∂T

∂t

−



j=1



r=1

∂T

∂u

(4.432)

We ﬁnd that

∂T

∂t

= mlv

φ cos t (4.433)

274 Equations of motion: differential approach

and



j=1



r=1

∂T

∂u

=−mlv

φ cos t (4.434)

Hence,

E = 0 and E = T is a constant of the motion even though T is an explicit function

of time. Note that the kinetic energy is a homogeneous quadratic function of the us.

Comparing the three methods which were presented for analyzing this rheonomic non-

holonomic system, the ﬁrst method using the fundamental dynamical equation for a system

of particles would seem to be preferable. It provides a minimum set of equations of motion

without Lagrange multipliers. Furthermore, the energy rate is found to be zero by inspection.

4.8 Summary of differential methods

In the study of differential methods in the dynamics of systems of particles or rigid bod-

ies, it is well to begin with Newton’s law of motion. Angular momentum methods can

also be employed, resulting in Euler’s equations for the rotational motion of rigid bod-

ies. These elementary approaches frequently require the introduction of constraint forces

and moments as additional variables in the dynamical equations, thereby complicating the

analysis.

Lagrange’s equations, when applied to holonomic systems with independent qs, result

in a minimum set of equations of motion without the necessity of solving for constraint

forces. In other words, although one set of qs may be subject to holonomic constraints,

another set of qs can be found which are independent and are consistent with the previous

constraints. No generalized constraint forces enter into the Lagrange equations of motion

for this system.

On the other hand, if there are nonholonomic constraints, then more qs are required than

the number of degrees of freedom. The use of the Lagrangian procedure involves Lagrange

multipliers which are associated with generalized constraint forces. If there are nqs and m

constraint equations, one obtains n second-order dynamical equations in addition to the m

constraint equations.

The use of Maggi’s equation eliminates the Lagrange multipliers and results in (n − m)

second-order equations of motion plus the m constraint equations. The Lagrange and Maggi

methods have the disadvantages, however, that the kinetic energy cannot be written in terms

of quasi-velocities, and must be written for the unconstrained system.

In the efﬁcient representation of dynamical systems, it is desirable to obtain a minimal

setof(n − m) ﬁrst-order differential equations of motion. This is possible in the general

nonholonomic case if one uses independent quasi-velocities as velocity variables. The

remaining four differential methods discussed in this chapter all result in a minimal set of

dynamical equations. The use of the Boltzmann–Hamel equation is the most complicated of

these methods and requires that the kinetic energy be written for the unconstrained system

having n degrees of freedom. The other three methods allow one to assume a constrained

system with (n − m) degrees of freedom from the beginning.

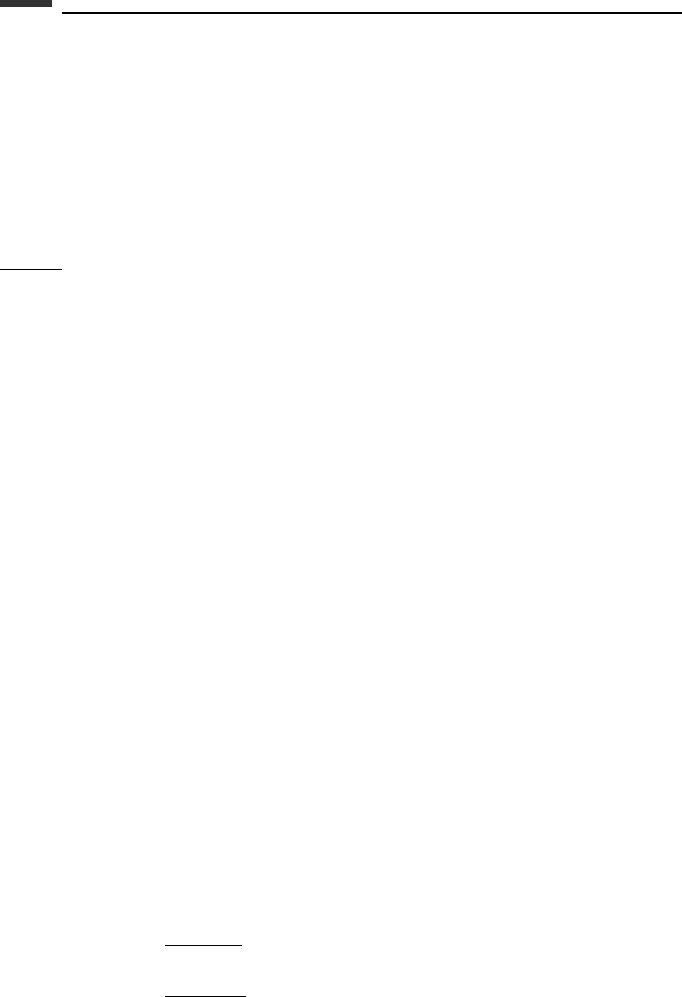
275 Summary of differential methods

Energy rate expressions can be obtained in several forms, depending upon the type of

dynamical equations used in their derivation. Each of these expressions can be used to obtain

a set of sufﬁcient conditions for a conservative system, that is, a system having a constant

energy function E. In the usual case, E = T

− T

+ V rather than the total energy T + V .

If the equations of motion for a given system are being integrated numerically, the energy

rate

E can be used as a check on the calculations. This is accomplished by integrating

separately with respect to time, and comparing the change in the energy E with that obtained

from the integrated solutions to the equations of motion.

A note on quasi-velocities

We have deﬁned quasi-velocities (us) in accordance with the equations



i=1



(q, t)

+ 

(q, t)(j = 1,...,n) (4.435)

where the right-hand sides are not integrable, in general. Moreover, we assumed that these

equations can be solved for the

qs, resulting in



j=1



(q, t)u

+ 

(q, t)(i = 1,...,n) (4.436)

Thus, we have assumed that the us and

qs are related linearly. If there are m linear non-

holonomic constraints, these are represented by setting the last mus equal to zero. The

remaining (n − m) us are independent.

Furthermore, we have expressed velocities and angular velocities in accordance with the

linear relations



j=1

(q, t)u

+ γ

(q, t) (4.437)



j=1

(q, t)u

+ β

(q, t) (4.438)

and we note that the γs and βs can be used in writing the differential equations of motion.

It is possible, however, to deﬁne the us in a way such that, in general, the

qs are nonlinear

functions of the us. For a system with nqs and m independent nonholonomic constraints, one

can deﬁne the (n − m) independent usasa set of parameters which specify the operating

point in velocity space, that is,

q-space. This operating point must lie on each of the m

constraint surfaces in velocity space, and therefore on their common intersection.

We need to ﬁnd expressions for the γs and βs in writing the equations of motion,

but the linear equations (4.437) and (4.438) are no longer valid for the more general us.

Nevertheless, we can use

(q, u, t) =

∂v

(q, u, t)

∂u

(4.439)

(q, u, t) =

∂ω

(q, u, t)

∂u

(4.440)

276 Equations of motion: differential approach

Agivensetofus may not have uniform dimensions, and so the question now arises

concerning how the corresponding Qs are to be found. One can use virtual work or, in this

case, virtual power to evaluate the Qs. For example, if a system of N particles has a force

applied to the ith particle (i = 1,...,N ), then, using virtual velocities,



i=1

· δv

n−m



j=1

δu

(4.441)

where

δv

n−m



j=1

∂v

∂u

δu

n−m



j=1

δu

(4.442)

Then, since the δus are independent, we obtain



i=1

· γ

( j = 1,...,n − m) (4.443)

Example 4.14 Consider the simple case of a particle of mass m which has a force F

applied to it. Let us choose (v, θ, φ)asus to represent the velocity vector v of the particle

in three-dimensional velocity space (Fig. 4.10).

This is similar to the use of spherical coordinates to designate a position in ordinary

3-space. The unit vectors e

, e

form an orthogonal triad with e

= e

× e

. In place of

(4.436) we have the equations

x = v sin θ cos φ (4.444)

y = v sin θ sin φ (4.445)

z = v cos θ (4.446)

Figure 4.10.

277 Summary of differential methods

which are nonlinear in the us. Conversely, we ﬁnd that

= v =



(4.447)

= θ = cos

−1



(4.448)

= φ = tan

−1

(4.449)

which are nonlinear and replace (4.435).

First method Let us use the general dynamical equation in the form



i=1

· γ

= Q

(4.450)

The velocity is

v = ve

(θ,φ) (4.451)

and the velocity coefﬁcients, obtained by using (4.439), are

= e

, γ

= v

∂e

∂θ

= ve

, γ

= v

∂e

∂φ

= v sin θ e

(4.452)

Note that the γs can be functions of the us in contrast to (4.437).

The particle acceleration is

v = ˙ve

+ v

= ˙ve

+ v

θe

+ v

φ sin θ e

(4.453)

and the force F, in terms of its components, is

F = F

+ F

(4.454)

Hence, using (4.443), we ﬁnd that

= F

, Q

= F

v, Q

= F

v sin θ (4.455)

Finally, using (4.450), the v equation is

m ˙v = F

(4.456)

Similarly, the θ equation is

θ = F

(4.457)

The φ equation is

φ sin

θ = F

v sin θ

278 Equations of motion: differential approach

φ sin θ = F

(4.458)

Actually, knowing

v, these equations of motion could have been obtained directly by

applying Newton’s law in the three orthogonal directions.

Second method Let us consider the Gibbs–Appell equation

∂ S

∂

= Q

(4.459)

where, in this case,

S =

m[˙v

+ (v

θ)

+ (v

φ sin θ )

] (4.460)

The v equation of motion is

∂ S

∂ ˙v

= m ˙v = F

(4.461)

The θ equation is

∂ S

∂

= mv

θ = F

v (4.462)

θ = F

(4.463)

The φ equation is

∂ S

∂

= mv

φ sin

θ = F

v sin θ (4.464)

φ sin θ = F

(4.465)

We see that the Gibbs–Appell method is quite direct when applied to this example.

4.9 Bibliography

Desloge, E. A. Classical Mechanics, Vol. 2. New York: John Wiley and Sons, 1982.

Greenwood, D. T. Principles of Dynamics, 2nd edn. Englewood Cliffs, NJ: Prentice-Hall, 1988.

Kane, T. R. and Levinson, D. A. Dynamics: Theory and Applications. New York: McGraw-Hill, 1985.

Neimark, Ju. I. and Fufaev, N. A. Dynamics of Nonholonomic Systems. Translations of Mathematical

Monographs, Vol. 33. Providence, RI: American Mathematical Society, 1972.

Papastavridis, J. G. Analytical Mechanics. Oxford: Oxford University Press, 2002.

Pars, L. A. A Treatise on Analytical Dynamics. London: William Heinemann, 1965.