Greenwood D.T. Advanced Dynamics
Подождите немного. Документ загружается.

249 A fundamental equation
y
x
m
m
e
n
e
t
v
l
φ
(x, y)
1
2
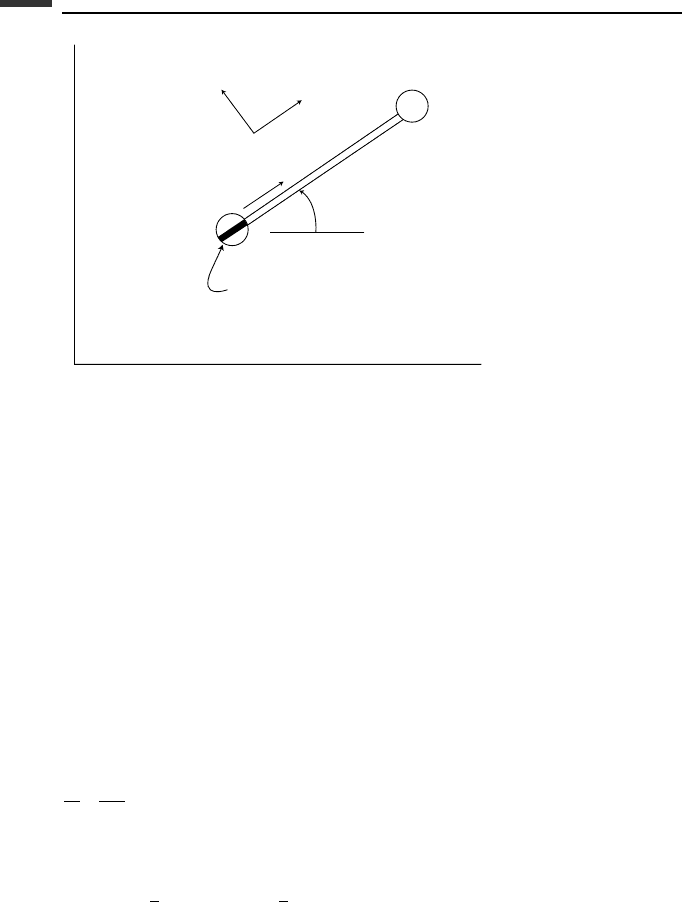
Figure 4.6.
equation (4.226) or (4.227) is more efficient than the Boltzmann–Hamel equation in this
general case.
Example 4.8 Let us consider once again the motion of a dumbbell (Fig. 4.6) as it moves on
the horizontal xy-plane. There is a knife-edge constraint acting on a particle whose location
is (x , y). Let the generalized coordinates be (x, y,φ) and choose
u
1
= v =
˙
x cos φ +
˙
y sin φ (4.229)
u
2
=
˙
φ (4.230)
u
3
=−
˙
x sin φ +
˙
y cos φ = 0 (4.231)
The first two us are independent and define the motion, while u
3
represents the constraint
function which is set equal to zero, indicating no slipping perpendicular to the knife edge.
We shall use the fundamental equation in the form applying to a system of particles.
d
dt
∂T
∂u
j
−
N
i=1
m
i
v
i
· ˙γ
ij
= Q
j
( j = 1,...,n − m) (4.232)
The constrained kinetic energy is
T = mu
2
1
+
1
2
ml
2
u
2
2
= mv
2
+
1
2
ml
2
˙
φ
2
(4.233)
since the particle velocities are
v
1
= ve
t
, v
2
= ve
t
+l
˙
φe
n
(4.234)

250 Equations of motion: differential approach
The corresponding velocity coefficients are
γ
11
=
∂v
1
∂v
= e
t
γ
12
=
∂v
1
∂
˙
φ
= 0
γ
21
=
∂v
2
∂v
= e
t
γ
22
=
∂v
2
∂
˙
φ
= le
n
(4.235)
The unit vectors rotate in the xy-plane with an angular velocity
˙
φ,so
˙γ
11
=
˙
φe
n
˙γ
12
= 0
˙γ
21
=
˙
φe
n
˙γ
22
=−l
˙
φe
t
(4.236)
There are no applied forces for motion in the xy-plane, so
Q
1
= 0, Q
2
= 0 (4.237)
Now we can use (4.232) to obtain the u
1
or v equation of motion. It is
2m ˙v − [mve
t
· (
˙
φe
n
) +m(ve
t
+l
˙
φe
n
) ·(
˙
φe
n
)] = 0
or
2m ˙v − ml
˙
φ
2
= 0 (4.238)
In a similar manner, one obtains the u
2
equation, namely,
ml
2
¨
φ + mlv
˙
φ = 0 (4.239)
These equations of motion are the same as were obtained in Example 4.4, on page 232,
by using the Boltzmann–Hamel equation. Here, however, their derivation is more direct.
Example 4.9 Consider the rolling disk problem of Example 4.6 on page 240. Let us use
the fundamental equation in the form given by (4.227), namely,
d
dt
∂T
∂u
j
−
N
i=1
(p
i
· ˙γ
ij
+ H
ci
·
˙
β
ij
) = Q
j
( j = 1,...,n − m) (4.240)
As in Fig. 4.2, let us choose the Euler angles (φ,θ,ψ)asqs and let the independent usbe
u
1
=
˙
θ, u
2
= ω
d
=
˙
φ sin θ, u
3
= =
˙
φ cos θ +
˙
ψ (4.241)
The velocity of the center of the disk is
v =−re
θ
+r
˙
θe
ψ
(4.242)
and the angular velocity is
ω =
˙
θe
θ
+ ω
d
e
d
+ e
ψ
(4.243)
The moments of inertia about the center are
I
a
=
1
2
mr
2
, I
t
=
1
4
mr
2
(4.244)

251 A fundamental equation
Thus, we find that the constrained kinetic energy is
T =
1
2
m(r
2
2
+r
2
˙
θ
2
) +
1
4
mr
2
2
+
1
8
mr
2
˙
θ
2
+ ω
2
d
=
5
8
mr
2
˙
θ
2
+
1
8
mr
2
ω
2
d
+
3
4
mr
2
2
(4.245)
The velocity coefficients are
γ
11
=
∂v
∂
˙
θ
= r e
ψ
, γ
12
=
∂v
∂ω
d
= 0, γ
13
=
∂v
∂
=−re
θ
(4.246)
and the angular velocity coefficients are
β
11
=
∂ω
∂
˙
θ
= e
θ
, β
12
=
∂ω
∂ω
d
= e
d
, β
13
=
∂ω
∂
= e
ψ
(4.247)
The e
θ
, e
d
, e
ψ
unit vector triad rotates due to
˙
φ and
˙
θ, resulting in an angular velocity
ω
c
=
˙
θe
θ
+
˙
φ(sin θ e
d
+ cos θ e
ψ
)
=
˙
θe
θ
+ ω
d
e
d
+ ω
d
cot θ e
ψ
(4.248)
where we notice that ω
d
=
˙
φ sin θ. Thus, we find that
˙
e
θ
= ω
c
× e
θ
= ω
d
cot θ e
d
− ω
d
e
ψ
(4.249)
˙
e
d
= ω
c
× e
d
=−ω
d
cot θ e
θ
+
˙
θe
ψ
(4.250)
˙
e
ψ
= ω
c
× e
ψ
= ω
d
e
θ
−
˙
θe
d
(4.251)
Now we can evaluate
˙γ
11
= r
˙
e
ψ
= r ω
d
−r
˙
θe
d
(4.252)
˙γ
12
= 0 (4.253)
˙γ
13
=−r
˙
e
θ
=−rω
d
cot θ e
d
+rω
d
e
ψ
(4.254)
and we note that
˙
β
11
=
˙
e
θ
,
˙
β
12
=
˙
e
d
,
˙
β
13
=
˙
e
ψ
(4.255)
The linear momentum is
p = mv =−mre
θ
+ mr
˙
θe
ψ
(4.256)
and the angular momentum about the center of mass is
H
c
= I
t
˙
θe
θ
+ I
t
ω
d
e
d
+ I
a
e
ψ
=
1
4
mr
2
˙
θe
θ
+
1
4
mr
2
ω
d
e
d
+
1
2
mr
2
e
ψ
(4.257)
The generalized applied forces due to gravity, obtained by using potential energy or virtual
work, are
Q
1
=−mgr cos θ, Q
2
= 0, Q
3
= 0 (4.258)
252 Equations of motion: differential approach
Now we are prepared to use (4.240) to obtain the differential equations of motion. The θ
equation is
5
4
mr
2
¨
θ +
3
2
mr
2
ω
d
−
1
4
mr
2
ω
2
d
cot θ =−mgr cos θ (4.259)
Similarly, the ω
d
equation is
1
4
mr
2
˙ω
d
+
1
4
mr
2
˙
θω
d
cot θ −
1
2
mr
2
˙
θ = 0 (4.260)
The equation is
3
2
mr
2
˙
− mr
2
˙
θω
d
= 0 (4.261)
These equations are identical with (4.174)–(4.176) obtained earlier by the general dy-
namical equation. Both methods involve about the same amount of effort.
Volterra’s equation
It is of some interest to note that Volterra’s equation for a system of particles, pub-
lished in 1898, is equivalent to a special case of the fundamental equation in the form
of (4.220).
Consider a system of N particles whose configuration is given by the 3N inertial Cartesian
coordinates (x
1
,...,x
3N
). Suppose there are m constraint equations which are linear in the
˙
xs. Choose ν = 3N − m independent us which are related to the
˙
xs by the scleronomic
equations
˙
x
i
=
ν
s=1
is
(x )u
s
(i = 1,...,3N) (4.262)
The kinetic energy of the constrained system is
T (x, u) =
1
2
3N
i=1
m
i
˙
x
2
i
=
1
2
3N
i=1
ν
k=1
ν
r=1
m
i
ik
ir
u
k
u
r
(4.263)
Volterra’s equation for this system of N particles is
d
dt
∂T
∂u
s
+
ν
k=1
ν
r=1
b
k
rs
− b
k
sr
u
k
u
r
−
3N
l=1
∂T
∂x
l
ls
= Q
s
(s = 1,...,ν) (4.264)
where
b
k
rs
=
3N
i=1
3N
j=1
m
i
ik
∂
ir
∂x
j
js
(k, r, s = 1,...,ν) (4.265)
We note that
∂T
∂x
l
=
3N
i=1
m
i
˙
x
i
∂
˙
x
i
∂x
l
=
3N
i=1
ν
k=1
ν
r=1
m
i
ik
∂
ir
∂x
l
u
k
u
r
(4.266)

253 A fundamental equation
Hence, in (4.264), the term
−
3N
l=1
∂T
∂x
l
ls
=−
3N
i=1
3N
l=1
ν
k=1
ν
r=1
m
i
ik
∂
ir
∂x
l
ls
u
k
u
r
=−
ν
k=1
ν
r=1
b
k
rs
u
k
u
r
(4.267)
and the Volterra equation can be written in the simpler form
d
dt
∂T
∂u
s
−
ν
k=1
ν
r=1
b
k
sr
u
k
u
r
= Q
s
(s = 1,...,ν) (4.268)
or
d
dt
∂T
∂u
s
−
3N
i=1
3N
j=1
ν
k=1
ν
r=1
m
i
ik
∂
is
∂x
j
jr
u
k
u
r
= Q
s
(s = 1,...,ν) (4.269)
We wish to express this result using vector notation. The velocity of the first particle is
v
1
=
3
i=1
ν
k=1
ik
u
k
e
i
(4.270)
where e
1
, e
2
, e
3
are inertially-fixed orthogonal unit vectors. The velocity coefficients for the
first particle are
γ
1s
=
∂v
1
∂u
s
=
3
i=1
is
(x )e
i
(s = 1,...,ν) (4.271)
Hence,
˙γ
1s
=
3
i=1
3N
j=1
ν
r=1
∂
is
∂x
j
jr
u
r
e
i
(s = 1,...,ν) (4.272)
For the first particle, noting that m
1
= m
2
= m
3
,wehave
m
1
v
1
· ˙γ
1s
=
3
i=1
3N
j=1
ν
k=1
ν
r=1
m
i
ik
∂
is
∂x
j
jr
u
k
u
r
(s = 1,...,ν) (4.273)
Finally, sum (4.273) over all N particles. Then using (4.269), we see that Volterra’s
equation in vector form is
d
dt
∂T
∂u
s
−
N
l=1
m
l
v
l
· ˙γ
ls
= Q
s
(s = 1,...,ν) (4.274)
But this is just the fundamental dynamical equation for a system of particles.
We conclude that Volterra’s equation is a special case of the fundamental equation for
a scleronomic system of particles, a case in which Cartesian coordinates are used as qs.
When Volterra’s equation was published, the concept of quasi-velocities was unknown,
so the us were regarded as
˙
qs. Equation (4.274), however, is more general and can be
used with rheonomic systems that are described using n generalized coordinates with m
nonholonomic constraints. The ν = n − m quasi-velocities are independent and the kinetic
energy is written for the constrained system.

254 Equations of motion: differential approach
4.6 The Gibbs–Appell equation
System of particles
Let us consider a system of N particles whose configuration is specified by nqs. The particle
velocities for a system with m nonholonomic constraints are given by (n − m) independent
us. Thus, the absolute velocity of the ith particle is
v
i
=
n−m
j=1
γ
ij
(q, t) u
j
+ γ
it
(q, t)(i = 1,...,N ) (4.275)
and the constrained kinetic energy is
T (q, u, t) =
1
2
N
i=1
m
i
v
2
i
(4.276)
The absolute particle accelerations, obtained by differentiating (4.275), are
˙
v
i
=
n−m
j=1
(γ
ij
˙
u
j
+ ˙γ
ij
u
j
) + ˙γ
it
(i = 1,...,N) (4.277)
where the ˙γs are linear functions of the us due to the equations
˙
q
k
=
n−m
l=1
kl
u
l
+
kt
(k = 1,...,n) (4.278)
Thus, we see that the acceleration
˙
v
i
is linear in the
˙
us and quadratic in the us.
Now let us introduce the Gibbs–Appell function
S(q, u,
˙
u, t) =
1
2
N
i=1
m
i
˙
v
2
i
(4.279)
which is obtained by substituting
˙
v
i
from (4.277) for v
i
in the kinetic energy expression of
(4.276). We see that
∂ S
∂
˙
u
j
=
N
i=1
m
i
˙
v
i
·
∂
˙
v
i
∂
˙
u
j
=
N
i=1
m
i
˙
v
i
· γ
ij
( j = 1,...,n − m) (4.280)
But, from the general dynamical equation (4.133), we have
N
i=1
m
i
˙
v
i
· γ
ij
= Q
j
( j = 1,...,n − m) (4.281)
Finally, from (4.280) and (4.281) we obtain
∂ S
∂
˙
u
j
= Q
j
( j = 1,...,n − m) (4.282)
which is the Gibbs–Appell equation for a system of particles. This equation was discovered
by Gibbs in 1879 and was studied in detail by Appell in an 1899 publication. It provides a

255 The Gibbs–Appell equation
minimal set of dynamical equations which are applicable to systems with quasi-velocities
and nonholonomic constraints.
To emphasize an important point, recall that the Gibbs–Appell function is obtained by
substituting
˙
v
i
for v
i
in the kinetic energy expression, where
˙
v
i
is the absolute acceleration
of the ith particle. One cannot in general, obtain S by writing T (q,
˙
q, t) and then substituting
¨
qsfor
˙
qs. Furthermore, since (4.282) involves differentiations with respect to the
˙
us, any
terms in S(q, u,
˙
u, t) which do not contain
˙
us can be omitted.
Example 4.10 Let us return to the dumbbell problem of Fig. 4.6. As independent quasi-
velocities consistent with the knife-edge constraint we choose
u
1
= v, u
2
=
˙
φ (4.283)
The particle velocities are
v
1
= ve
t
, v
2
= ve
t
+l
˙
φe
n
(4.284)
and the corresponding accelerations are
˙
v
1
= ˙ve
t
+ v
˙
φe
n
(4.285)
˙
v
2
= (˙v −l
˙
φ
2
)e
t
+ (l
¨
φ + v
˙
φ)e
n
(4.286)
The resulting Gibbs–Appell function is
S =
1
2
m
˙
v
2
1
+
˙
v
2
2
=
1
2
m[˙v
2
+ v
2
˙
φ
2
+ (˙v −l
˙
φ
2
)
2
+ (l
¨
φ + v
˙
φ)
2
] (4.287)
The generalized applied forces are
Q
1
= 0, Q
2
= 0 (4.288)
Now we can apply (4.282) and obtain the following equations of motion:
∂ S
∂
˙
u
1
=
∂ S
∂ ˙v
= m(2˙v − l
˙
φ
2
) = 2m ˙v − ml
˙
φ
2
= 0 (4.289)
∂ S
∂
˙
u
2
=
∂ S
∂
¨
φ
= ml(l
¨
φ + v
˙
φ) = ml
2
¨
φ + mlv
˙
φ = 0 (4.290)
It is apparent that, for this problem, the Gibbs–Appell method is quite efficient in pro-
ducing the differential equations of motion.
System of rigid bodies
Now let us generalize the Gibbs–Appell function to give correct equations of motion for a
system of N rigid bodies when (4.282) is used. Let v
i
be the velocity of the reference point
of the ith body, and let I
i
be the inertia dyadic about this reference point. The total kinetic
energy is
T =
1
2
N
i=1
m
i
v
2
i
+
1
2
N
i=1
ω
i
· I
i
· ω
i
+
N
i=1
m
i
v
i
· ˙ρ
ci
(4.291)
256 Equations of motion: differential approach
A Gibbs–Appell function which yields correct equations of motion for this system of
rigid bodies is
S(q, u,
˙
u, t) =
1
2
N
i=1
m
i
˙
v
2
i
+
N
i=1
1
2
˙ω
i
· I
i
· ˙ω
i
+ ω
i
× (I
i
· ω
i
) · ˙ω
i
+
N
i=1
m
i
˙
v
i
· ¨ρ
ci
(4.292)
where
¨ρ
ci
= ˙ω
i
× ρ
ci
+ ω
i
× (ω
i
× ρ
ci
) (4.293)
and we note that I
i
is symmetric. In the evaluation of ∂ S/∂
˙
u
j
, only terms involving
˙
v
i
,˙ω
i
,
or ¨ρ
ci
need be considered. Recall that
∂
˙
v
i
∂
˙
u
j
=
∂v
i
∂u
j
= γ
ij
(4.294)
∂ ˙ω
i
∂
˙
u
j
=
∂ω
i
∂u
j
= β
ij
(4.295)
Also,
˙
v
i
·
∂ ˙ω
i
∂
˙
u
j
× ρ
ci
= ρ
ci
×
˙
v
i
· β
ij
(4.296)
Then, from (4.282) and (4.292), we obtain
∂ S
∂
˙
u
j
=
N
i=1
m
i
(
˙
v
i
+ ¨ρ
ci
) ·γ
ij
+
N
i=1
[I
i
· ˙ω
i
+ ω
i
× (I
i
· ω
i
) +m
i
ρ
ci
×
˙
v
i
] ·β
ij
= Q
j
( j = 1,...,n − m) (4.297)
which is the general dynamical equation for a system of rigid bodies. It results in (n − m)
first-order dynamical equations.
If one takes the reference point of each rigid body at its center of mass, then ρ
ci
= 0 and
the Gibbs–Appell function becomes
S =
1
2
N
i=1
m
i
˙
v
2
i
+
N
i=1
1
2
˙ω
i
· I
ci
· ˙ω
i
+ ω
i
× (I
ci
· ω
i
) · ˙ω
i
(4.298)
where I
ci
is the inertia dyadic about the center of mass. An equivalent form is
S =
1
2
N
i=1
m
i
˙
v
2
i
+
˙
H
ci
· ˙ω
i
+ ω
i
× H
ci
· ˙ω
i
(4.299)
where H
ci
is the angular momentum of the ith body about its center of mass.
Example 4.11 Consider the rolling disk problem of Fig. 4.2. We again choose the inde-
pendent quasi-velocities
u
1
=
˙
θ, u
2
= ω
d
, u
3
= (4.300)

257 The Gibbs–Appell equation
The angular velocity of the disk is
ω =
˙
θe
θ
+ ω
d
e
d
+ e
ψ
(4.301)
and the angular velocity of the e
θ
e
d
e
ψ
unit vector triad is equal to
˙
φ +
˙
θ or
ω
c
=
˙
θe
θ
+ ω
d
e
d
+ ω
d
cot θ e
ψ
(4.302)
and we note that e
θ
remains horizontal. Thus, we find that
˙
e
θ
= ω
c
× e
θ
= ω
d
cot θ e
d
− ω
d
e
ψ
(4.303)
˙
e
d
= ω
c
× e
d
=−ω
d
cot θ e
θ
+
˙
θe
ψ
(4.304)
˙
e
ψ
= ω
d
e
θ
−
˙
θe
d
(4.305)
and
˙ω =
¨
θ − ω
2
d
cot θ + ω
d
e
θ
+ (˙ω
d
+
˙
θω
d
cot θ −
˙
θ) e
d
+
˙
e
ψ
(4.306)
The velocity of the center of the disk is
v =−re
θ
+r
˙
θe
ψ
(4.307)
and the corresponding acceleration is
˙
v = (−r
˙
+ r
˙
θω
d
) e
θ
− (rω
d
cot θ + r
˙
θ
2
) e
d
+ (r
¨
θ + rω
d
) e
ψ
(4.308)
Hence, we see that
˙
v
2
= (r
˙
− r
˙
θω
d
)
2
+ (rω
d
cot θ + r
˙
θ
2
)
2
+ (r
¨
θ + rω
d
)
2
(4.309)
The disk has moments of inertia
I
a
=
1
2
mr
2
, I
t
=
1
4
mr
2
(4.310)
Thus, the angular momentum about the center is
H
c
=
1
4
mr
2
˙
θe
θ
+
1
4
mr
2
ω
d
e
d
+
1
2
mr
2
e
ψ
(4.311)
Upon differentiating with respect to time, we find that
˙
H
c
=
1
4
mr
2
¨
θ − ω
2
d
cot θ + 2ω
d
e
θ
+(˙ω
d
+
˙
θω
d
cot θ − 2
˙
θ)e
d
+ 2
˙
e
ψ
(4.312)
In addition,
ω × H
c
=
1
4
mr
2
(ω
d
e
θ
−
˙
θe
d
) (4.313)
258 Equations of motion: differential approach
Now we can use (4.299) to obtain the Gibbs–Appell function. If we omit terms not
containing
˙
us, it is
S =
1
2
mr
2
[(
˙
−
˙
θω
d
)
2
+ (
¨
θ + ω
d
)
2
]
+
1
8
mr
2
¨
θ − ω
2
d
cot θ + 2ω
d
¨
θ − ω
2
d
cot θ + ω
d
+(˙ω
d
+
˙
θω
d
cot θ − 2
˙
θ)( ˙ω
d
+
˙
θω
d
cot θ −
˙
θ)
+
1
4
mr
2
˙
2
+
1
8
mr
2
(ω
d
¨
θ −
˙
θ˙ω
d
) (4.314)
The generalized applied forces are
Q
1
=−mgr cos θ, Q
2
= 0, Q
3
= 0 (4.315)
The differential equations of motion are obtained from
∂ S
∂
˙
u
j
= Q
j
( j = 1, 2, 3) (4.316)
The θ equation is
∂ S
∂
¨
θ
= mr
2
(
¨
θ + ω
d
) +
1
8
mr
2
2
¨
θ − 2ω
2
d
cot θ + 4ω
d
=
5
4
mr
2
¨
θ −
1
4
mr
2
ω
2
d
cot θ +
3
2
mr
2
ω
d
=−mgr cos θ (4.317)
The ω
d
equation is
∂ S
∂ ˙ω
d
=
1
4
mr
2
(˙ω
d
+
˙
θω
d
cot θ − 2
˙
θ) = 0 (4.318)
Finally, the equation is
∂ S
∂
˙
=
3
2
mr
2
˙
− mr
2
˙
θω
d
= 0 (4.319)
These three dynamical equations constitute a minimum set for this system. The effort
required in their derivation is about the same as for the general dynamical equation.
Principle of least constraint
The principle of least constraint was discovered by Gauss in 1829, and thereby preceded
the Gibbs–Appell equations, to which it is related, by half a century. The principle of least
constraint is an algebraic minimization principle which leads to the differential equations
of motion. Briefly, it states that a certain function of the constraint forces is minimized by
the actual motion, as compared with other motions which, at any given time, have the same
configuration and velocities, but have small variations in the accelerations.
Consider a system of N particles whose configuration is given by 3N Cartesian coordi-
nates relative to an inertial frame. Suppose there are m equations of constraint, holonomic
