Greenwood D.T. Advanced Dynamics

Подождите немного. Документ загружается.

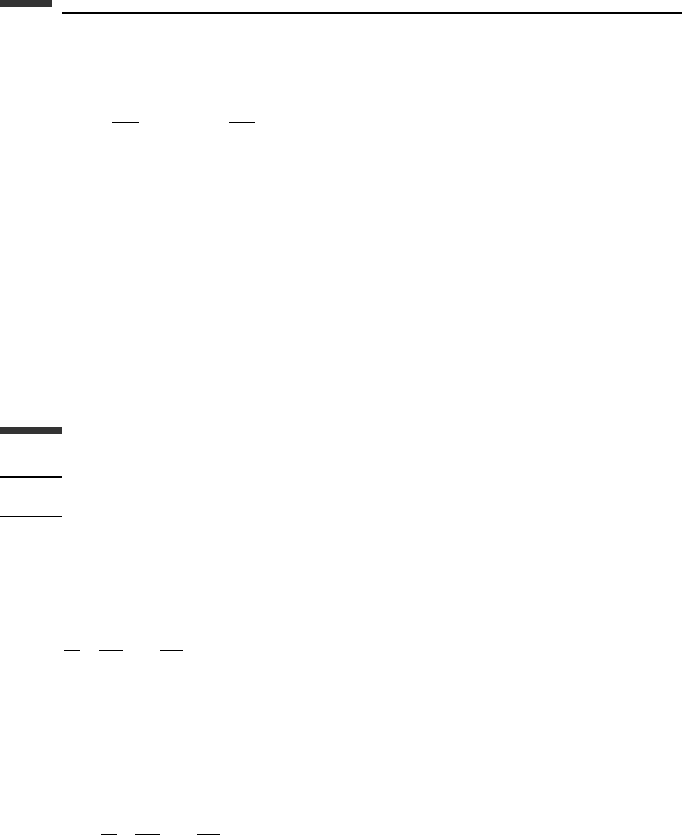
219 Maggi’s equation

(q, t) = 0 (4.10)

and (4.6) applies, where



∂φ

∂q

,

∂φ

∂t

(4.11)

Using the notation of (4.5) and (4.6), virtual displacements are constrained in accordance

with

δθ



i=1



(q, t)δq

= 0(j = n − m + 1,...,n) (4.12)

In velocity space, we have



i=1



(q, t)δw

= 0(j = n − m + 1,...,n) (4.13)

implying that any virtual velocity δw lies in the common intersection of the constraint planes

in velocity space.

4.2 Maggi’s equation

Derivation of Maggi’s equation

Consider a mechanical system whose conﬁguration is described by nqs and which has m

nonholonomic constraints with the linear form of (4.6). One approach to the problem of

obtaining differential equations of motion is to use Lagrange’s equation in the multiplier

form of (2.49), namely,



∂T

∂



−

∂T

∂q

= Q



j=n−m+1



(i = 1,...,n) (4.14)

These n second-order equations plus the m ﬁrst-order constraint equations comprise a

total of (n + m) equations to solve for the nqs and m λs as functions of time. Frequently,

however, one is not interested in the λ solutions, and would prefer a method which eliminates

the λs from the beginning. The use of Maggi’s equation is one such method.

Let us begin with Lagrange’s principle, that is,



i=1





∂T

∂



−

∂T

∂q

− Q



δq

= 0 (4.15)

where the δqs satisfy the virtual constraints of (4.12) and we note that the kinetic energy

T (q,

q, t) is written for the unconstrained system. The virtual displacements of quasi-

coordinates and true coordinates are related by

δθ



i=1



(q, t)δq

( j = 1,...,n) (4.16)

220 Equations of motion: differential approach

or, upon inversion,

δq

n−m



j=1



(q, t)δθ

(i = 1,...,n) (4.17)

where, from (4.12), the last m δθs are equal to zero.

Now substitute this expression for δq

into (4.15). We obtain

n−m



j=1



i=1





∂T

∂



−

∂T

∂q

− Q





δθ

= 0 (4.18)

The ﬁrst (n − m) δθsareindependent so each coefﬁcient must equal zero. The result is

Maggi’s equation (1896).



i=1





∂T

∂



−

∂T

∂q







i=1



( j = 1,...,n − m) (4.19)

The term on the right represents the generalized applied force associated with the quasi-

coordinate δθ

. The set of Maggi equations are (n − m) second-order differential equations

in (q,

q, t). In addition, there are m equations of constraint, making a total of n equations

to solve for the nqs as functions of time.

The 

coefﬁcients are not unique but are chosen in such a way that the ﬁrst (n − m)

δθs are independent and are consistent with the constraints. In the resulting Φ matrix, each

column represents the amplitude ratios of an independent set of δqs which could be used

in Lagrange’s principle, equation (4.15). Maggi’s equation uses the ﬁrst (n − m) columns

of Φ to obtain the (n − m) differential equations of motion.

Example 4.1 Two particles, each of mass m, are connected by a massless rod of length l

(Fig. 4.1). There is a knife-edge constraint at particle 1 which prevents a velocity component

perpendicular to the rod at that point. We wish to use Maggi’s equation to ﬁnd the differential

equations of motion.

(x, y)

Figure 4.1.

221 Maggi’s equation

Let (x , y,φ) be chosen as generalized coordinates. As quasi-velocities (us) let us take

= v =

x cos φ +

y sin φ (4.20)

φ (4.21)

=−

x sin φ +

y cos φ = 0 (4.22)

where u

= 0 is the nonholonomic constraint equation and (u

, u

) are independent. Thus,

we obtain the coefﬁcient matrix

Ψ =







cos φ sin φ 0

001

−sin φ cos φ 0







(4.23)

for the unconstrained system. The inverse matrix is

Φ = Ψ

−1







cos φ 0 −sin φ

sin φ 0 cos φ

01 0







(4.24)

We shall use Maggi’s equation, (4.19), in the form



i=1





∂T

∂



−

∂T

∂q





= 0(j = 1, 2) (4.25)

because all Qs are equal to zero. The unconstrained kinetic energy is obtained by using

(3.140). It is

T = m



−l

φ sin φ + l

φ cos φ



(4.26)

We ﬁnd that



∂T

∂



= m(2

x −l

φ sin φ − l

cos φ),

∂T

∂x

= 0 (4.27)



∂T

∂



= m(2

y +l

φ cos φ − l

sin φ),

∂T

∂y

= 0 (4.28)



∂T

∂



= m(l

φ −l

x sin φ + l

y cos φ − l

φ cos φ − l

φ sin φ) (4.29)

∂T

∂φ

= m(−l

φ cos φ − l

φ sin φ) (4.30)

The ﬁrst equation of motion, using Maggi’s equation and involving (4.27), (4.28) and the

ﬁrst column of the Φ matrix, is

m(2

x −l

φ sin φ − l

cos φ) cos φ + m(2

y +l

φ cos φ − l

sin φ) sin φ = 0

222 Equations of motion: differential approach

m(2

x cos φ + 2

y sin φ − l

) = 0 (4.31)

The second equation of motion, involving the second column of the Φ matrix, is



∂T

∂



−

∂T

∂φ

= m(l

φ −l

x sin φ + l

y cos φ) = 0 (4.32)

In addition, (4.22), the constraint equation, can be differentiated with respect to time to

yield,

x sin φ −

y cos φ +

φ cos φ +

φ sin φ = 0 (4.33)

In equations (4.31)–(4.33) we have three equations linear in the

qs. Thus, we can solve for

φ which are then integrated numerically to obtain the response as a function of time.

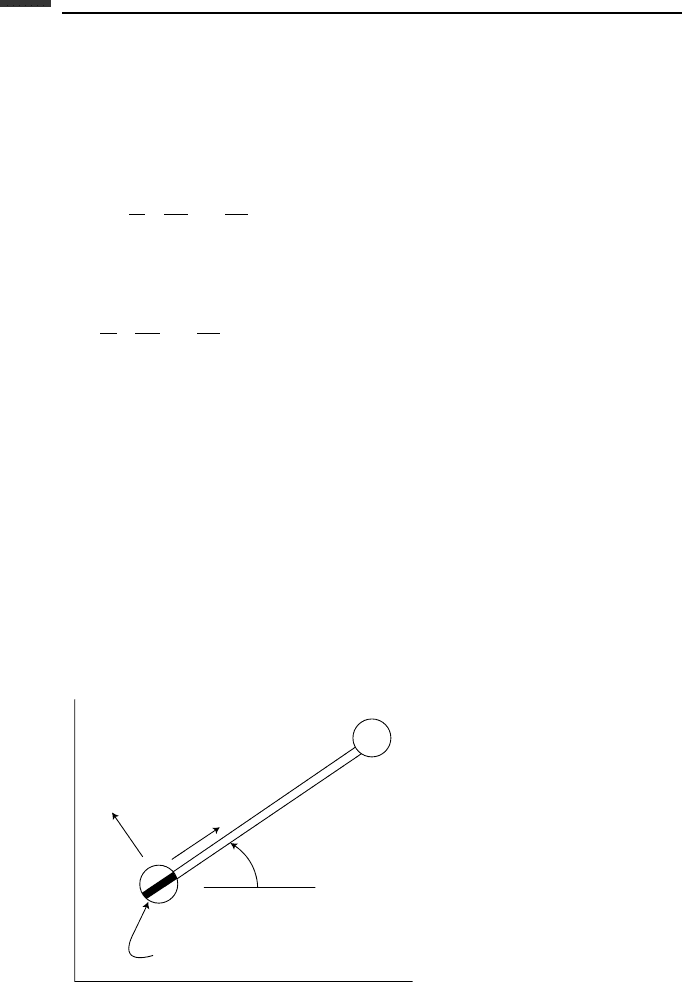
Example 4.2 Now consider a more complex problem, the rolling motion of a disk on

a horizontal plane. Suppose that the classical Euler angles (φ,θ,ψ) are used to specify

the orientation of a disk of mass m and radius r, whose contact point C has Cartesian

coordinates (x , y), (Fig. 4.2).

Let us choose the independent us to be the Euler angle rates. Thus,

φ, u

θ, u

ψ (4.34)

(x, y)

␪

⭈

␺

⭈

␾

⭈

␺

Figure 4.2.

223 Maggi’s equation

The constraint equations, which enforce no slipping at the contact point, are

x +r

ψ cos φ = 0 (4.35)

y +r

ψ sin φ = 0 (4.36)

Maggi’s equation is



i=1





∂T

∂



−

∂T

∂q







i=1



( j = 1,...,n − m) (4.37)

where, in this case, the only nonzero Q is

=−mgr cos θ (4.38)

The coefﬁcients in (4.34)–(4.36) result in

Ψ =







10 0 00

01 0 00

00 1 00

00r cos φ 10

00r sin φ 01







(4.39)

for the order (

φ,

θ,

ψ,

y). The inverse matrix is

Φ = Ψ

−1







10 0 00

01 0 00

00 1 00

00−r cos φ 10

00−r sin φ 01







(4.40)

In terms of the Cartesian unit vectors i, j, k, the velocity of the center of the unconstrained

disk is

v = (

x −r

φ cos φ cos θ + r

θ sin φ sin θ)i

y −r

φ sin φ cos θ − r

θ cos φ sin θ)j +r

θ cos θ k (4.41)

The angular velocity is

ω = (

φ cos θ +

ψ)e

θe

φ sin θ e

(4.42)

In accordance with Koenig’s theorem, the kinetic energy is

T =

ω · I · ω (4.43)

224 Equations of motion: differential approach

where the axial and transverse moments of inertia are

, I

(4.44)

about the center of the disk. Thus, the total unconstrained kinetic energy is

T =

) +

(1 +5 cos

θ) +

ψ cos θ − mr

φ cos φ cos θ + mr

θ sin φ sin θ

−mr

φ sin φ cos θ − mr

θ cos φ sin θ (4.45)

Next, let us apply the Lagrangian operator with respect to each of the generalized coor-

dinates. We obtain



∂T

∂



−

∂T

∂φ

φ(1 +5 cos

θ) +

ψ cos θ

−mr

x cos φ cos θ − mr

y sin φ cos θ

−

θ sin θ cos θ −

ψ sin θ (4.46)



∂T

∂



−

∂T

∂θ

θ + mr

x sin φ sin θ − mr

y cos φ sin θ

sin θ cos θ +

ψ sin θ (4.47)



∂T

∂



−

∂T

∂ψ

ψ +

φ cos θ −

θ sin θ (4.48)



∂T

∂



−

∂T

∂x

= m

x −mr

φ cos φ cos θ

+mr

θ sin φ sin θ + mr

sin φ cos θ

+mr

sin φ cos θ + 2mr

θ cos φ sin θ (4.49)



∂T

∂



−

∂T

∂y

= m

y − mr

φ sin φ cos θ

−mr

θ cos φ sin θ − mr

cos φ cos θ

−mr

cos φ cos θ + 2mr

θ sin φ sin θ (4.50)

A substitution into (4.37), using the ﬁrst three columns of the Φ matrix, yields the Maggi

equations. The φ equation is

φ(1 +5 cos

θ) +

ψ cos θ − mr

x cos φ cos θ

−mr

y sin φ cos θ −

θ sin θ cos θ −

ψ sin θ = 0 (4.51)

225 Maggi’s equation

The θ equation is

θ + mr

x sin φ sin θ − mr

y cos φ sin θ

sin θ cos θ +

ψ sin θ =−mgr cos θ (4.52)

The ψ equation is

ψ +

φ cos θ −

θ sin θ − mr(

x cos φ +

y sin φ) = 0 (4.53)

There are two additional equations obtained by differentiating the constraint equations

(4.35) and (4.36) with respect to time.

x +r

ψ cos φ − r

ψ sin φ = 0 (4.54)

y +r

ψ sin φ + r

ψ cos φ = 0 (4.55)

In (4.51)–(4.55) we have ﬁve differential equations which are linear in the

qs. They can

be solved for the

qs and then integrated to yield the motion as given by φ,θ,ψ, x and y as

functions of time.

A simpliﬁcation can be made if we solve (4.54) for

x and (4.55) for

y, and then substitute

into the Maggi equations. In (4.51) we ﬁnd that

−mr cos θ(

x cos φ +

y sin φ) = mr

ψ cos θ (4.56)

and the φ equation reduces to

φ(1 +5 cos

θ) +

ψ cos θ

−

θ sin θ cos θ −

ψ sin θ = 0 (4.57)

Similarly,

mr sin θ(

x sin φ −

y cos φ) = mr

ψ sin θ (4.58)

and the θ equation becomes

θ +

sin θ cos θ +

ψ sin θ =−mgr cos θ (4.59)

Finally, from (4.53) and (4.56), we ﬁnd that the ψ equation is

ψ +

φ cos θ −

θ sin θ = 0 (4.60)

In (4.57), (4.59), and (4.60) we have reduced the original set of ﬁve differential equations

to three dynamical equations in the Euler angles. This is a minimum set for this system.

226 Equations of motion: differential approach

4.3 The Boltzmann–Hamel equation

We have seen that the Lagrangian approach does not produce correct equations of motion

if the kinetic energy is expressed in terms of quasi-velocities rather than true velocities.

The question arises whether we can add terms to Lagrange’s equation to produce correct

equations in this more general case. The answer is yes, but at the cost of some additional

complications.

Derivation

Let us consider an unconstrained system whose kinetic energy is expressed in the form

T (q,

q, t), that is, using true velocities (

qs). We know that the fundamental form of La-

grange’s equation applies, namely,



∂T

∂



−

∂T

∂q

= Q

(i = 1,...,n) (4.61)

We wish to introduce quasi-velocities (us) in place of the

qs. To accomplish this aim, let

us ﬁrst assume scleronomic transformation equations of the form



i=1



(q)

( j = 1,...,n) (4.62)

or, conversely,



j=1



(q)u

(i = 1,...,n) (4.63)

The kinetic energy will be the same in value, whether expressed in terms of

qsorus, but

will be different in form. So let us write

∗

(q, u, t) = T (q,

q, t) (4.64)

where T

∗

is the kinetic energy expressed in terms of quasi-velocities.

First, let us consider

∂T

∂



j=1

∂T

∗

∂u

∂



j=1

∂T

∗

∂u



(4.65)

Thus, we obtain



∂T

∂





j=1



∂T

∗

∂u







j=1



k=1

∂T

∗

∂u

∂

∂q

(4.66)

Then, using (4.63),



∂T

∂





j=1



∂T

∗

∂u







j=1



k=1



l=1

∂T

∗

∂u

∂

∂q



(4.67)

227 The Boltzmann–Hamel equation

Furthermore, we see that

∂T

∂q

∂T

∗

∂q



j=1

∂T

∗

∂u

∂q

∂T

∗

∂q



j=1



k=1

∂T

∗

∂u

∂

∂q

∂T

∗

∂q



j=1



k=1



l=1

∂T

∗

∂u

∂

∂q



(4.68)

Thus, starting with Lagrange’s equation (4.61), and using (4.67) and (4.68), we obtain



j=1



∂T

∂u





−

∂T

∗

∂q



j=1



k=1



l=1

∂T

∗

∂u



∂

∂q

−

∂

∂q





= Q

(4.69)

where Q

is the generalized applied force associated with q

Next, multiply (4.69) by 

and sum over i.Now



i=1





= δ

(4.70)

since Φ = Ψ

−1

and δ

is the Kronecker delta. Thus we obtain the result that



∂T

∗

∂u



−



i=1

∂T

∗

∂q





i=1



j=1



k=1



l=1

∂T

∗

∂u



∂

∂q

−

∂

∂q





= Q

∗

(r = 1,...,n) (4.71)

where

∗



i=1

∂

∂u



i=1



(4.72)

is the generalized applied force associated with the quasi-velocity u

Equation (4.71) is the basic result, giving the n differential equations of motion in terms

of quasi-velocities. For convenience, however, we shall introduce notation which will give

it a simpler appearance. First, we deﬁne the Hamel coefﬁcients

(q) =−γ

≡



i=1



k=1



∂

∂q

−

∂

∂q





(4.73)

Let us use the notation

∂T

∗

∂θ



i=1

∂T

∗

∂q

∂θ



i=1

∂T

∗

∂q

∂

∂u



i=1

∂T

∗

∂q



(4.74)

Finally, for convenience, let us drop the asterisks, but assume that T = T (q, u, t). Then

(4.71) has the form



∂T

∂u



−

∂T

∂θ



j=1



l=1

∂T

∂u

= Q

(r = 1,...,n) (4.75)

228 Equations of motion: differential approach

This is the Boltzmann–Hamel equation, published in 1904, for systems described in terms

of quasi-velocities, and assuming independent qs and us. Notice that the added term, com-

pared to Lagrange’s equation, actually involves a quadruple summation, implying increased

complexity. On the other hand, if the us are true velocities, then (4.62) is integrable for all

j and thus all the γ

parameters vanish. Then (4.75) reduces to Lagrange’s equation with

the θs representing true coordinates.

Now consider a scleronomic system with m nonholonomic constraints. The last mus

are chosen such that the constraints are applied by setting these mus equal to zero,

that is,



i=1



(q)

= 0(j = n − m + 1,...,n) (4.76)

Equation (4.75) is still valid, except that there are now only (n − m) independent us, cor-

responding to the (n − m) degrees of freedom. Thus, we have



∂T

∂u



−

∂T

∂θ



j=1

n−m



l=1

∂T

∂u

= Q

(r = 1,...,n − m) (4.77)

In addition to these (n − m) ﬁrst-order dynamical equations, there are n ﬁrst-order kine-

matical equations of the form

n−m



j=1



(q)u

(i = 1,...,n) (4.78)

Thus, there are a total of (2n − m) ﬁrst-order differential equations to solve for the nqs and

the (n − m) nonzero us.

This is a minimal set of equations. One should note that the kinetic energy T (q, u, t)

must be written for the full, unconstrained set of nus. All n partial derivatives of the form

∂T /∂u

must be calculated. After this has been completed, the last mus can be set equal

to zero.

A generalization of the Boltzmann–Hamel equation can be obtained for systems in which

the equations for the ushavetherheonomic form



i=1



(q, t)

+ 

(q, t)(j = 1,...,n − m) (4.79)



i=1



(q, t)

+ 

(q, t) = 0(j = n − m + 1,...,n) (4.80)

Again, the last m equations represent nonholonomic constraints, in general. In addition, we

have

n−m



j=1



(q, t)u

+ 

(q, t)(i = 1,...,n) (4.81)