Greenwood D.T. Advanced Dynamics
Подождите немного. Документ загружается.

199 Impulsive motion
and we note that the entire Y matrix is n × n. The input mass at u
1
for
ˆ
Q
2
= 0is
m
1
=
1
Y
11
(3.372)
Now let us consider a second primed system with an input u
2
and an output u
3
. For this
system, we have
u
2
= Y
22
ˆ
Q
2
+ Y
23
ˆ
Q
3
(3.373)
u
3
= Y
32
ˆ
Q
2
+ Y
33
ˆ
Q
3
(3.374)
Finally, let us connect the two systems in accordance with the constraint equation
u
2
= u
2
(3.375)
as shown in Fig. 3.15b. Then the impulse
ˆ
Q
2
is actually due to the constraint and is not
imposed from outside the system. Furthermore, due to Newton’s law of action and reaction,
we have
ˆ
Q
2
=−
ˆ
Q
2
(3.376)
Equating the right-hand sides of (3.371) and (3.373), and setting
ˆ
Q
3
equal to zero,
we obtain
Y
21
ˆ
Q
1
+ Y
22
ˆ
Q
2
= Y
22
ˆ
Q
2
=−Y
22
ˆ
Q
2
or
ˆ
Q
2
=−
Y
21
Y
22
+ Y
22
ˆ
Q
1
(3.377)
Then, using (3.370), we have
u
1
=
Y
11
−
Y
12
Y
21
Y
22
+ Y
22
ˆ
Q
1
(3.378)
Since the Y matrix is symmetric, the input or driving-point mass for the combined system
is
m
1
=
ˆ
Q
1
u
1
=
Y
22
+ Y
22
Y
11
(Y
22
+ Y
22
) −Y
2
12
(3.379)
In general, the self-admittances Y
11
, Y
22
and Y
22
are positive and Y
12
is nonzero. Hence,
the input mass at u
1
is increased, in general, by connecting a second system. The exceptions
are that
m
1
is unchanged if Y
12
= 0, or if the input mass of the second system is zero, that
is, Y
22
is infinite.
Notice that the effect of connecting the second system is to attach its input mass
m
2
=
1
Y
22
(3.380)
at u
2
. This results in an impulse
ˆ
Q
2
acting on the first system, where
ˆ
Q
2
=−
ˆ
Q
2
=−m
2
u
2
=−
u
2
Y
22
(3.381)
200 Kinematics and dynamics of a rigid body
Then, upon substituting into (3.370) and (3.371), we can solve for u
1
in agreement with
(3.378) and obtain
m
1
as before.
The energy input to an initially motionless system due to a single impulse
ˆ
Q
i
at u
i
is
equal to the work
W =
1
2
ˆ
Q
i
u
i
(3.382)
where, from (3.369),
u
i
=
ˆ
Q
i
m
i
(3.383)
Thus, we obtain
W =
ˆ
Q
2
i
2m
i
=
1
2
m
i
u
2
i
(3.384)
This, by the principle of work and kinetic energy, must equal the total kinetic energy of the
system. Hence, we can find the kinetic energy without explicitly solving for all the usif
we use the concept of input mass. Note that the work done by an impulse on an initially
motionless system is always positive or zero.
More generally, the work done by a single impulse
ˆ
Q
i
onamovingsystemis
W =
ˆ
Q
i
u
i0
+
1
2
u
i
=
ˆ
Q
i
u
i0
+
ˆ
Q
2
i
2m
i
(3.385)
Again, the work is equal to
ˆ
Q
i
multiplied by the average velocity at u
i
. In this case, however,
the work may be positive or negative, depending on the value of u
i0
, the velocity just before
the impulse.
An interesting consequence of the symmetry of the Y matrix is the reciprocity of impulsive
responses. Thus, the response u
j
due to a unit impulse
ˆ
Q
i
is equal to the response u
i
due to a unit impulse
ˆ
Q
j
, in accordance with (3.368) and Y
ij
= Y
ji
.
Example 3.10 Two rods, each of mass m and length l, are connected by a pin joint at
B (Fig. 3.16). When the system is in a straight configuration, a transverse impulse
ˆ
F
1
is
applied at A. We wish to solve for the responses u
1
, u
2
, u
3
, as well as the driving-point
mass at u
1
.
u
1
ω
1
ω
2
u
2
u
3
C
m
B
m
l
A
F
1
^
l
Figure 3.16.
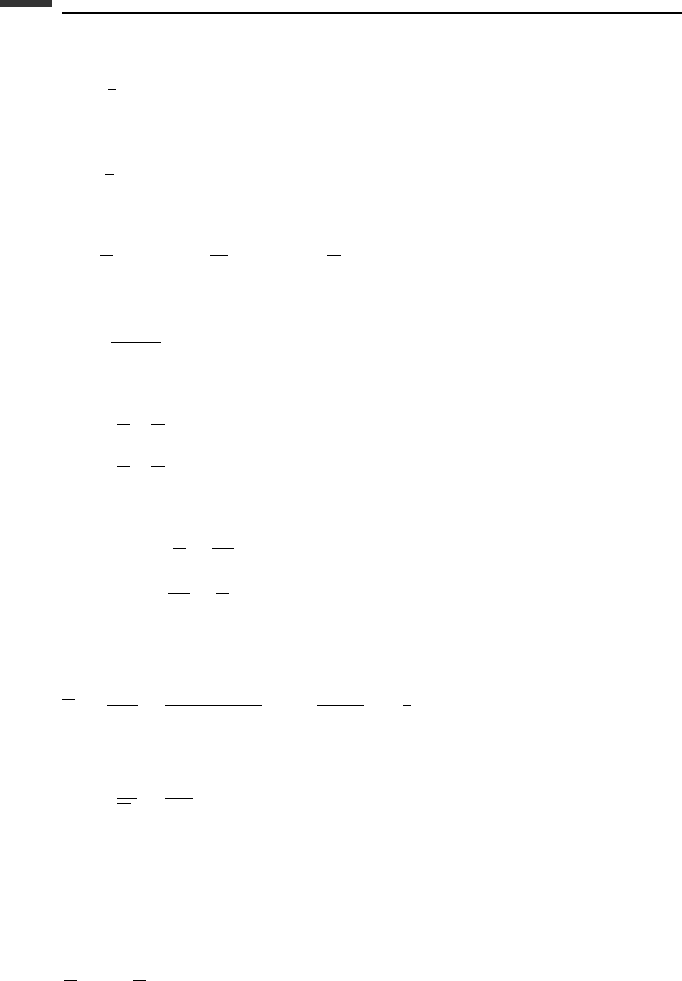
201 Impulsive motion
First method First consider the rod AB separately. The velocity of its center of mass is
v
c1
=
1
2
(u
1
+ u
2
) (3.386)
and its angular velocity is
ω
1
=
1
l
(u
2
− u
1
) (3.387)
Hence, its kinetic energy is
T =
m
8
(u
1
+ u
2
)
2
+
m
24
(u
2
− u
1
)
2
=
m
6
u
2
1
+ u
2
2
+ u
1
u
2
(3.388)
With the aid of (3.331), namely,
m
ij
=
∂
2
T
∂u
i
∂u
j
(3.389)
we obtain the mass matrix
m =
m
3
m
6
m
6
m
3
(3.390)
The inverse matrix is
Y = m
−1
=
4
m
−2
m
−2
m
4
m
(3.391)
These m and Y matrices apply to rods AB and BC individually.
If we now connect the two rods, the driving-point mass at u
1
is given by (3.379)
m
1
=
ˆ
F
1
u
1
=
2Y
22
2Y
11
Y
22
− Y
2
12
= m
8
32 −4
=
2
7
m (3.392)
Furthermore,
u
1
=
ˆ
F
1
m
1
=
7
ˆ
F
1
2m
(3.393)
Let us return to the basic equation
n
j=1
m
ij
u
j
=
ˆ
Q
i
(3.394)
and apply it to rod AB in the combined system. We obtain
m
3
u
1
+
m
6
u
2
=
ˆ
F
1
(3.395)
202 Kinematics and dynamics of a rigid body
Knowing u
1
, we find that
u
2
=−
ˆ
F
1
m
(3.396)
In addition, for rod AB,
ˆ
Q
2
=
m
6
u
1
+
m
3
u
2
=
1
4
ˆ
F
1
(3.397)
where
ˆ
Q
2
is actually the constraint impulse applied to rod AB at B.
Finally, for rod BC, noting the law of action and reaction at B,wehave
m
3
u
2
+
m
6
u
3
=−
ˆ
Q
2
=−
1
4
ˆ
F
1
(3.398)
from which we obtain
u
3
=
ˆ
F
1
2m
(3.399)
This result is in agreement with the second motion equation for rod BC, namely,
m
6
u
2
+
m
3
u
3
= 0 (3.400)
Second method Let us consider the complete system from the beginning. Referring to
(3.388) and adding over the two rods, the kinetic energy of the system is
T =
m
6
u
2
1
+ u
2
2
+ u
1
u
2
+
m
6
u
2
2
+ u
2
3
+ u
2
u
3
=
m
6
u
2
1
+ 2u
2
2
+ u
2
3
+ u
1
u
2
+ u
2
u
3
(3.401)
Then, using (3.389), the mass matrix is
m =
m
3
m
6
0
m
6
2m
3
m
6
0
m
6
m
3
(3.402)
and, upon inversion,
Y =
7
2m
−
1
m
1
2m
−
1
m
2
m
−
1
m
1
2m
−
1
m
7
2m
(3.403)

203 Impulsive motion
Now we can use the general equation
u
j
=
n
i=1
Y
ji
ˆ
Q
i
(3.404)
and note that
ˆ
Q
1
=
ˆ
F
1
,
ˆ
Q
2
=
ˆ
Q
3
= 0 (3.405)
Here
ˆ
Q
2
is equal to zero because no external impulse is applied at B in the u
2
direction.
The constraint impulses at B are internal to the complete system.
From the first column of Y and (3.404), we obtain
u
1
=
7
ˆ
F
1
2m
,u
2
=−
ˆ
F
1
m
,u
3
=
ˆ
F
1
2m
(3.406)
in agreement with our previous results.
The second method appears to be simpler, but it involves the inversion of a larger ma-
trix. The second method avoids calculating constraint impulses, but they are thereby not
directly available. Thus, the choice of method depends upon the nature of the desired
results.
Example 3.11 As an example of reciprocity, let us consider the angular impulse response
of a rigid body. Let xyz be a principal axis system at the center of mass of the body. Suppose
an angular impulse
ˆ
M is applied about an arbitrary 1-axis which passes through the center
of mass. We wish to find the change ω
2
in the angular velocity component about a second
arbitrary 2-axis through the center of mass.
Let (c
1x
, c
1y
, c
1z
) be the direction cosines of the positive 1-axis relative to the xyz frame.
Similarly, let (c
2x
, c
2y
, c
2z
) specify the direction of the positive 2-axis. The response com-
ponents in the body-fixed Cartesian frame are
ω
x
=
c
1x
ˆ
M
I
xx
,ω
y
=
c
1y
ˆ
M
I
yy
,ω
z
=
c
1z
ˆ
M
I
zz
(3.407)
Now take the component of ω in the direction of the positive 2-axis. We obtain
ω
2
= c
2x
ω
x
+ c
2y
ω
y
+ c
2z
ω
z
=
c
1x
c
2x
I
xx
+
c
1y
c
2y
I
yy
+
c
1z
c
2z
I
zz
ˆ
M (3.408)
This is the angular velocity about the 2-axis due to an angular impulse
ˆ
M about the 1-axis.
If, on the other hand, we wish to find the response ω
1
about the 1-axis due to an angular
impulse
ˆ
M about the 2-axis, we merely interchange the 1 and 2 subscripts in (3.407) and
(3.408). But this leaves the right-hand side of (3.408) unchanged. Hence,
ω
1
= ω
2
(3.409)
204 Kinematics and dynamics of a rigid body
j
i
m, l
B
m, l
m, l
m, l
A
E
D
45 45
v
0
v
0
θ
1
θ
2
C
Figure 3.17.
and we confirm the reciprocity relation for the responses to angular impulses about two
arbitrary axes through the center of mass of a rigid body.
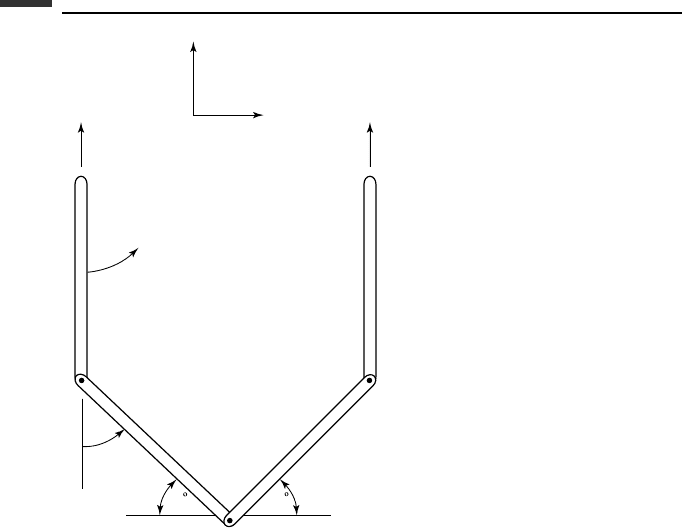
Example 3.12 A system consists of four rods, each of mass m and length l, which are
connected by pin joints, as shown in Fig. 3.17. The system is motionless until ends A and
E are suddenly given equal vertical velocities v
0
. We wish to find the resulting angular
velocities of the rods.
First, notice that the system is symmetrical about a vertical line through C. Thus, we can
consider only rods AB and BC which are the left half of the system. From the symmetry,
any motion of point C must be vertical and any interaction impulse at C must be horizontal.
The velocities of points A and B are
v
A
= v
0
j (3.410)
v
B
= l
˙
θ
1
i + v
0
j (3.411)
The kinetic energy of ABC is
T = T
AB
+ T
BC
(3.412)

205 Bibliography
where, using (3.339), we find that
T
AB
=
1
2
mv
2
0
+
1
6
ml
2
˙
θ
2
1
(3.413)
T
BC
=
1
2
m
v
2
0
+l
2
˙
θ
2
1
+
1
6
ml
2
˙
θ
2
2
+
ml
2
√
2
˙
θ
2
(l
˙
θ
1
+ v
0
) (3.414)
Thus,
T = mv
2
0
+
2
3
ml
2
˙
θ
2
1
+
1
6
ml
2
˙
θ
2
2
+
ml
2
2
√
2
˙
θ
1
˙
θ
2
+
mlv
0
2
√
2
˙
θ
2
(3.415)
The half-system has only one degree of freedom because of the constraint that the hori-
zontal velocity at C is equal to zero. The holonomic constraint equation is
l
˙
θ
1
+
1
√
2
l
˙
θ
2
= 0
or
˙
θ
2
=−
√
2
˙
θ
1
(3.416)
Hence, the kinetic energy is
T =
1
2
ml
2
˙
θ
2
1
−
1
2
mlv
0
˙
θ
1
+ mv
2
0
(3.417)
Note that
ˆ
Q
1
equals zero and use (3.367) to obtain
p
1
= p
1
=
∂T
∂
˙
θ
1
= ml
2
˙
θ
1
−
1
2
mlv
0
= 0 (3.418)
which results in
˙
θ
1
=
v
0
2l
,
˙
θ
2
=−
v
0
√
2l
(3.419)
By symmetry, rods DE and CD move as mirror images of AB and BC, respectively.
It is interesting to note that by setting ∂ T /∂
˙
θ
1
equal to zero in (3.418) we apply a
stationarity condition on T with respect to changes in the value of
˙
θ
1
. Actually, the kinetic
energy is a minimum consistent with the prescribed velocity v
0
, in accordance with Kelvin’s
theorem.
In general, Kelvin’s theorem states that if a system, initially at rest, is suddenly set into
motion by prescribed velocities at some of its points, the actual kinetic energy of the resulting
motion is a minimum compared to other kinematically possible motions.
3.5 Bibliography
Ginsberg, J. H. Advanced Engineering Dynamics, 2nd edn. Cambridge, UK: Cambridge University
Press, 1995.
Greenwood, D. T., Principles of Dynamics, 2nd edn. Englewood Cliffs, NJ: Prentice-Hall, 1988.
Kane, T. R. and Levinson, D. A. Dynamics: Theory and Applications. New York: McGraw-Hill, 1985.
206 Kinematics and dynamics of a rigid body
3.6 Problems
3.1. Let XYZ be an inertially-fixed frame and let xyz be the body-fixed frame of a rigid body.
Suppose the initial orientation of the body is given by the axis and angle variables
a = I = i and φ = 60
◦
. (a) Assuming that
˙
a = 0.1J and
˙
φ = 0, find the initial angular
velocity ω of the body, expressed in inertial and in body-fixed components. (b) Find
the initial values of C and
˙
C.
3.2. Obtain the rotational equations of motion for a general rigid body, assuming principal
axes and using type II Euler angles as generalized coordinates.
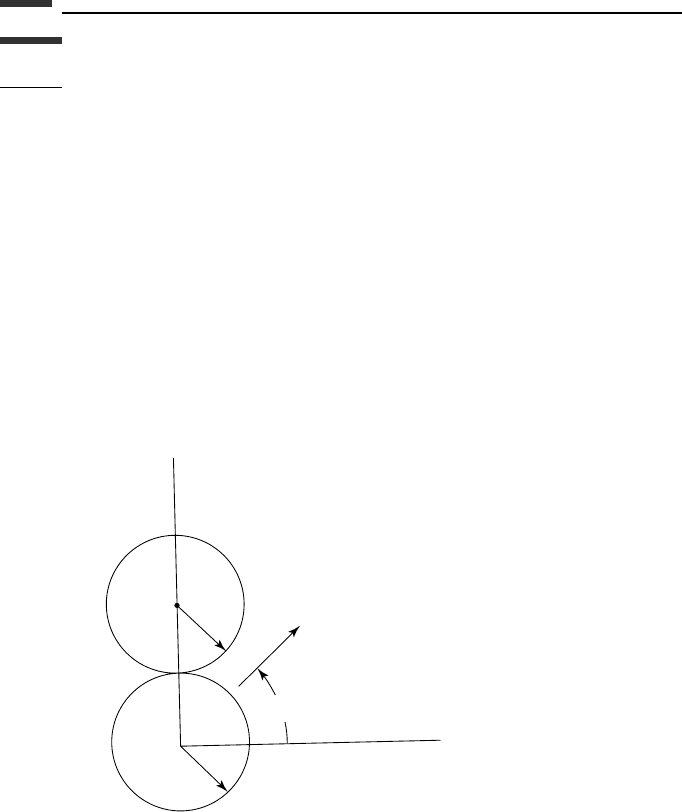
3.3. Two spheres, each of mass m, radius r, and moment of inertia I undergo impact, as
shown. Just before impact sphere 1 has a velocity v
0
at 45
◦
from the x-axis. Sphere
2 is initially motionless and neither sphere is rotating. (a) Assuming smooth spheres
and a coefficient of restitution e, solve for the velocities v
1
and v
2
of the two spheres
just after impact. (b) Repeat for the case in which there is a coefficient of friction
µ between the spheres, as well as a coefficient of restitution e. Also solve for the
resulting angular velocities ω
1
and ω
2
.
y
m
m
r
r
x
v
0
2
1
45
°
Figure P 3.3.
3.4. An axially-symmetric rocket has constant axial and transverse moments of inertia with
I
t
= 5I
a
. Initially the rocket is rotating about the symmetry axis (z-axis) at rad/s.
Due to a small thrust misalignment, a constant body-fixed moment M
y
is applied to
the rocket, where M
y
<< I
a
2
. (a) Assume the initial conditions ω
x
(0) = ω
y
(0) = 0
and solve for ω
x
and ω
y
as functions of time. (b) At what time does the symmetry
axis first return to its original orientation?
207 Problems
3.5. Use type I Euler angles to analyze the free rotational motion of a rigid body. (a)
Obtain equations for
˙
ψ,
˙
θ,
˙
φ in terms of ψ, θ, φ, assuming that the H vector points
upward in the direction of the negative Z -axis. (b) What do these equations reduce
to if the rigid body is symmetrical about its x-axis?
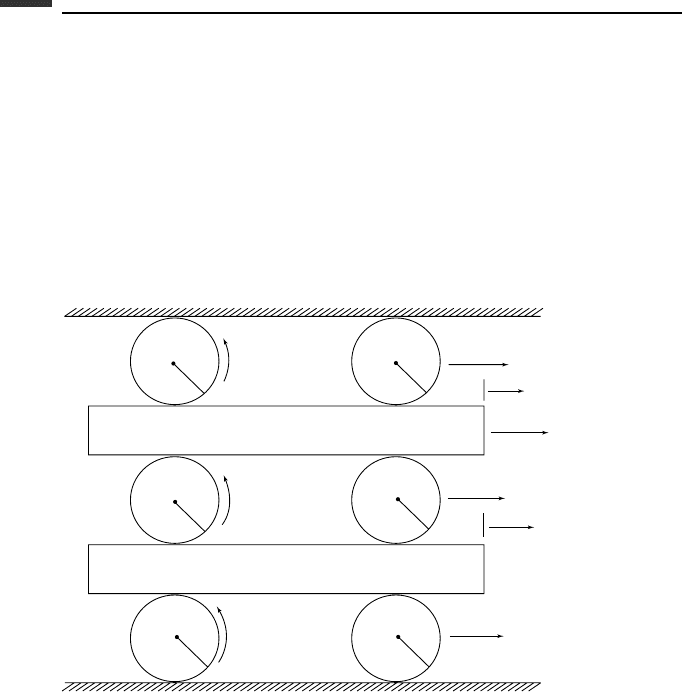
3.6. Two slabs, each of mass m
0
can translate on rollers, as shown. The rollers are uniform
cylinders, each of mass m and radius r, and they roll without slipping. The applied
force F is constant. (a) Obtain the differential equations of motion, using (x
1
, x
2
)as
generalized coordinates. (b) Suppose the system starts from rest with x
1
(0) = x
2
(0) =
0. Assuming that m
0
= 2m,solveforx
2
when x
1
= 1. (c) Solve for the horizontal
forces applied to the upper and lower faces of the lower slab.
m
r
m
r
m
r
m
r
ω
1
m
r
ω
2
m
r
ω
3
m
0
m
0
x
1
x
2
F
v
1
v
2
v
3
Figure P 3.6.
3.7. A rigid body of mass m has principal moments of inertia I
xx
= 3ma
2
, I
yy
=
4ma
2
, I
zz
= 5ma
2
about its center of mass. Initially the velocity of the center of mass
is zero and the angular velocity components are ω
x
(0) = ω
0
,ω
y
(0) = ω
z
(0) = 0.
Suddenly a point P at x = y = z = a is fixed, although there is free rotation about
P. Find (a) the values of ω
x
,ω
y
,ω
z
immediately after impact; (b) the final kinetic
energy.
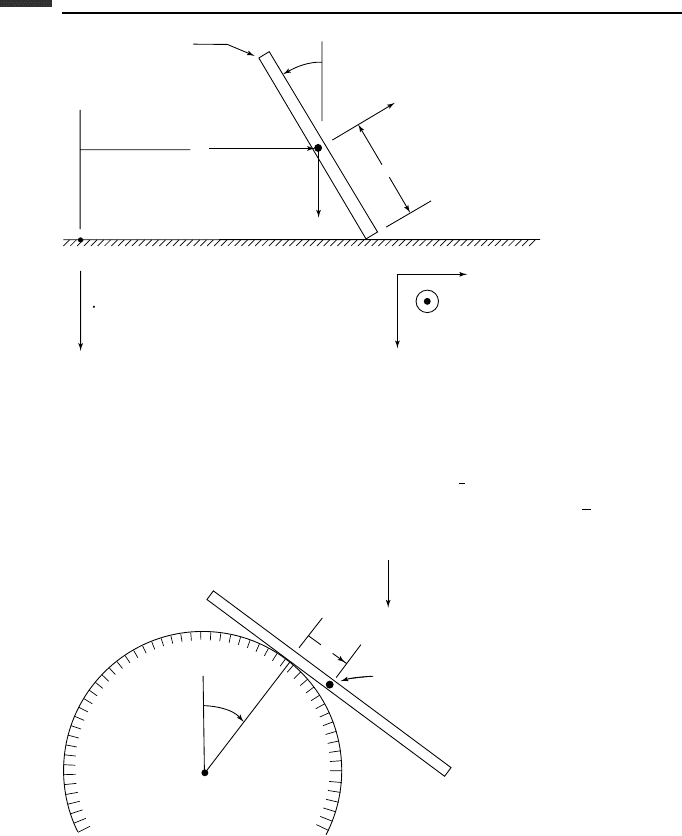
3.8. The center of mass of a thin circular disk of radius r , and with central moments of
inertia I
a
and I
t
, moves with constant speed around a circular path of radius R. The
plane of the disk is inclined at a constant angle θ from the vertical. Solve for the
required precession rate
˙
ψ.
208 Kinematics and dynamics of a rigid body
disk
R
mg
r
i
j
k
θ
Ω
ψ
Figure P 3.8.
3.9. A thin rod of mass m and length l slides and rotates on a fixed frictionless horizontal
cylinder of radius r.(a)Use(x,θ) as coordinates and obtain the differential equations
of motion. (b) Assume the initial conditions x(0) =
1
5
l,
˙
x(0) = 0,θ(0) = 0,
˙
θ(0) = 0
and show that the rod will lose contact with the cylinder when cos θ =
1
g
(r
˙
θ
2
+ 2
˙
x
˙
θ).
c.m.
m, l
x
g
r
O
θ
Figure P 3.9.
3.10. An axially symmetric rigid body of mass m has axial and transverse moments of
inertia I
a
and I
t
, where I
t
is taken about the fixed point O. The xyz coordinate system
has its origin at O and the x-axis is the axis of symmetry. The z-axis remains horizontal
