Greenwood D.T. Advanced Dynamics

Подождите немного. Документ загружается.

169 Basic rigid body dynamics

essentially a three-dimensional plot which gives the value of 1/

√

I for any axis passing

through the origin of the xyz frame. The major axis is the axis having the minimum moment

of inertia. Similarly, the minor axis is the axis having the maximum moment of inertia; it

is perpendicular to the major axis. These two axes plus an orthogonal third axis constitute

the set of three principal axes corresponding to the principal moments of inertia. The

orientations of the three principal axes are such that all products of inertia are equal to zero.

This means that the inertial coupling terms associated with products of inertia dissappear

and, for example, the generalized Euler equations (3.162) simplify to the standard equations

of (3.164).

Suppose we are given a general inertia dyadic I and we wish to calculate the principal

moments of inertia of the body. If a rigid body is rotating about a principal axis, then its

angular velocity and angular momentum are parallel, that is

H = I · ω = I ω (3.181)

where the proportionality constant I on the right is a principal moment of inertia.

Equation (3.181) has the form of an eigenvalue problem. In terms of dyadics we have



I − I U



· ω = 0 (3.182)

or, using matrix notation,





− I ) I

− I )

















(3.183)

We assume that ω = 0, so the determinant of the coefﬁcients must equal zero, that is,



− I ) I

− I )



= 0

(3.184)

This determinant yields a cubic equation in I known as the characteristic equation. Its three

real roots are the three principal moments of inertia.

For each root I the direction of the corresponding principal axis is found by solving

(3.183) for the ratios of the components of ω. These axes are also the principal axes of the

inertia ellipsoid of the body.

Example 3.3 Consider a rigid body having an inertia matrix

I =





28 −8 −4

−828−4

−4 −424





kg·m

(3.185)

with respect to a body-ﬁxed xyz frame. We wish to solve for the principal moments of

inertia and the directions of the corresponding principal axes. The characteristic equation

170 Kinematics and dynamics of a rigid body

is obtained from (3.184). It is



(28 − I ) −8 −4

−8(28− I ) −4

−4 −4(24− I )



= 0

(3.186)

− 80 I

+ 2032 I − 16 128 = 0 (3.187)

The roots of this characteristic equation are the values of the principal moments of inertia.

In increasing magnitude, they are

= 16, I

= 28, I

= 36 kg·m

(3.188)

The corresponding axis directions are obtained from (3.183), namely,

(28 − I )ω

− 8ω

− 4ω

= 0

−8ω

+ (28 − I )ω

− 4ω

= 0 (3.189)

−4ω

− 4ω

+ (24 − I )ω

= 0

All three equations must be satisﬁed, but usually any two equations are sufﬁcient to solve

for the ω ratios.

Assuming that no principal axis lies in the yz-plane, let us set ω

= 1. Then, for I

= 16

we obtain ω

= ω

= 1. For I

= 28 the result is ω

= ω

= 1, ω

=−2. The result

for I

= 36 is ω

= 1, ω

=−1, ω

= 0. Now let us normalize each set of ωstogivea

unit vector magnitude, resulting in a set of direction cosines for each principal axis. The

direction cosines can be combined to form the three rows of a rotation matrix C for rotation

from an original xyz frame to the principal x



frame. A system of labeling for the primed

axes which requires the least rotation is obtained by placing the most positive terms on the

main diagonal of C, possibly by multiplying a row by −1. We obtain







−

√

−1

√

−1

√







(3.190)

One can check that the principal moments of inertia are obtained from



= CIC

(3.191)

Also, to be sure of a right-handed principal coordinate system, one should check that the

determinant |C|=1.

Modiﬁed Euler equations

Sometimes it is convenient to use a rotational equation having a form similar to (3.161)

but being different in that strict body axes are not used. In general, suppose that H and M

171 Basic rigid body dynamics

are expressed in terms of unit vectors associated with a Cartesian frame having an angular

velocity ω

. Then the rotational equation has the vector form

(

+ ω

× H = M (3.192)

where (

is the time derivative of total angular momentum H , as viewed from the rotating

frame and assuming that the unit vectors ﬁxed in this frame have time derivatives equal to

zero.

An important application of this approach occurs in the case of an axially symmetric

rigid body. Let us assume that the x -axisofanxyz frame is the axis of symmetry, and the

reference point is chosen at the center of mass or at an inertially ﬁxed point on the axis

of symmetry. Let I

be the moment of inertia about the symmetry axis, whereas I

is the

moment of inertia about any transverse axis at the reference point.

Now suppose that the body rotates about the axis of symmetry with an angular velocity

or spin rate s measured relative to the xyz frame. If we let the angular velocity of the xyz

frame be

= ω

i + ω

j + ω

k (3.193)

we see that the angular momentum of the body is

H = I

(ω

+ s)i + I

j + I

k (3.194)

Also,

(

= I

(˙ω

s)i + I

˙ω

j + I

˙ω

k (3.195)

Then, substituting into (3.192), we obtain the modiﬁed Euler equations:

(˙ω

s) = I

˙ω = M

˙ω

− (I

− I

)ω

+ I

sω

= M

(3.196)

˙ω

+ (I

− I

)ω

− I

sω

= M

where the total spin , which is the total angular velocity about the symmetry axis, is

 = ω

+ s (3.197)

Until now the relative spin s has been arbitrary. For example, if we set s = 0, the modiﬁed

Euler equations revert to ordinary Euler equations for an axially symmetric body. But we

can choose s in such a way that the kinematics of solving for the orientation of axially

symmetric body is relatively easy. Let us use type I Euler angles and let ψ and θ specify

the orientation of the xyz frame. The inertial XYZ frame is chosen so that the XY-plane is

horizontal and the Z-axis is positive downward. Since the third Euler angle φ does not

affect the orientation of the xyz frame, its y-axis remains horizontal. This implies that the

horizontal component of ω

must lie along the y-axis, and we have the constraint equation

(see Fig. 3.7)

cos θ + ω

sin θ = 0 (3.198)

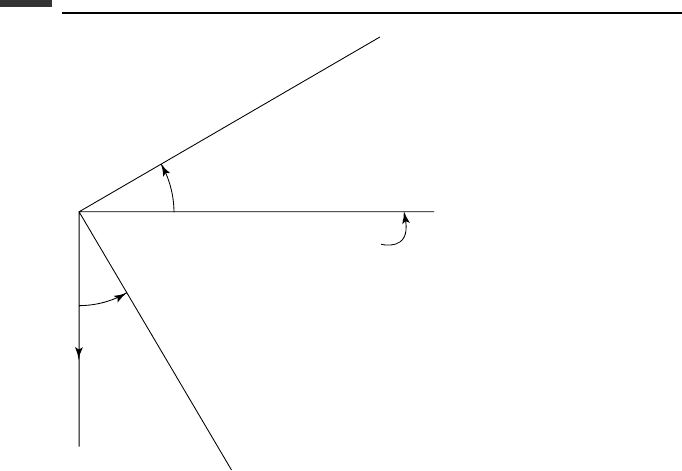
172 Kinematics and dynamics of a rigid body

XY plane

Figure 3.7.

=−ω

tan θ (3.199)

where we note that the xz-plane is vertical. The vertically downward component of ω

ψ, that is,

ψ =−ω

sin θ + ω

cos θ = ω

sec θ (3.200)

Also, we have

θ = ω

(3.201)

φ = s =  − ω

=  + ω

tan θ (3.202)

Now let us eliminate ω

and s from (3.196) and the modiﬁed Euler equations have the form

˙ω = M

(3.203)

˙ω

+ I

tan θ + I

ω

= M

(3.204)

˙ω

− I

tan θ − I

ω

= M

(3.205)

These three ﬁrst-order dynamical equations plus the three ﬁrst-order kinematical equations

(3.200)–(3.202) can be integrated numerically to obtain the Euler angles as functions of

time. Thus, we have obtained relatively simple equations for the rotational motion of an

173 Basic rigid body dynamics

axially-symmetric body. Note that the third terms in (3.204) and (3.205) are gyroscopic

coupling terms.

Another approach is to write the dynamical equations directly in terms of type I Euler

angles and their time derivatives. One can use

 =

φ −

ψ sin θ (3.206)

θ (3.207)

ψ cos θ (3.208)

and then (3.203)–(3.205) take the form

(

φ −

ψ sin θ −

θ cos θ ) = M

(3.209)

(

θ +

sin θ cos θ ) + I

ψ(

φ −

ψ sin θ ) cos θ = M

(3.210)

(

ψ cos θ − 2

θ sin θ ) − I

θ(

φ −

ψ sin θ ) = M

(3.211)

These three second-order dynamical equations are somewhat more complicated than those

obtained earlier in (3.203)–(3.205).

Finally, let us consider the rather common situation in which there is no applied moment

about the axis of symmetry, that is,

= 0 (3.212)

Then there are only two ﬁrst-order dynamical equations, namely,

˙ω

+ I

tan θ + I

ω

= M

(3.213)

˙ω

− I

tan θ − I

ω

= M

(3.214)

where the total spin  is constant.IfM

and M

are known as functions of (ψ, θ, t),

these dynamic equations plus the kinematic equations (3.200) and (3.201) can be integrated

numerically to give the orientation of the axis of symmetry as a function of time.

Example 3.4 As an example of an axially symmetric body with no moment applied about

its axis of symmetry, consider the motion of a top with a ﬁxed point under the action of

gravity (Fig. 3.8). The top has a constant total spin  and its center of mass lies at distance

l from its ﬁxed point O.

The differential equations of motion, obtained from (3.204) and (3.205), are

˙ω

+ I

tan θ + I

ω

=−mgl cos θ (3.215)

˙ω

− I

tan θ − I

ω

= 0 (3.216)

and we recall that

θ = ω

(3.217)

Let us consider the case of a top with a large spin  and assume that the axis of symmetry

remains nearly horizontal, that is, θ is small. In addition, assume that ω

and ω

are small.

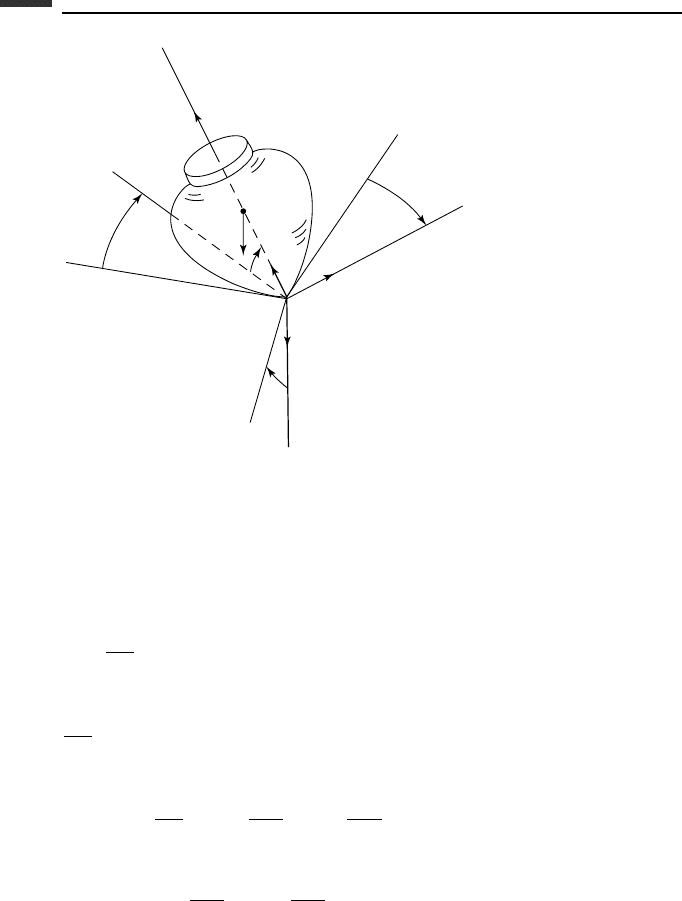
174 Kinematics and dynamics of a rigid body

Ω

c.m.

Figure 3.8.

Then, neglecting higher-order terms, (3.215) and (3.216) take the linear forms

˙ω

+ I

ω

=−mgl (3.218)

˙ω

− I

ω

= 0 (3.219)

Now differentiate (3.219) with respect to time, obtaining

˙ω



¨ω

(3.220)

and substitute into (3.218). The result is



¨ω

+ I

ω

=−mgl (3.221)

This differential equation has a solution of the general form

ψ =−

mgl



+ A cos

t

+ B sin

t

(3.222)

Then, from (3.219) we ﬁnd that

θ =−A sin

t

+ B cos

t

(3.223)

where the constants A and B are evaluated from initial conditions.

As a speciﬁc example, consider the case of cuspidal motion of a fast-spinning top or

gyroscope and assume that its symmetry axis is nearly horizontal. We have the initial

175 Basic rigid body dynamics

conditions

(0) = ω

(0) = 0 (3.224)

and obtain the solutions

θ =−

mgl



sin

t

(3.225)

ψ =−

mgl





1 −cos

t



(3.226)

Assuming the initial condition θ(0) = 0, (3.225) can be integrated to yield

θ =−

mgl





1 −cos

t



(3.227)

We have assumed that θ is small and  is large. More speciﬁcally, let us now assume

that 

>> I

mgl/I

. Then ω

and ω

will also be small, as we have assumed.

Aplotofθ versus ψ indicates that a point on the symmetry axis follows a cycloidal path

with upward-pointing cusps. The average precession rate is mgl/I

 and the frequency of

the sinusoidal nutational oscillation in θ is I

/I

Example 3.5 Let us use Euler’s equations to solve for the rotational motion of a rigid body

under the action of a constant applied moment relative to the body axes. Assume that the

principal moments of inertia are I

. There is a constant applied moment

about the z-axis and we assume that the initial conditions and the magnitude of M

are

such that ω

>> (ω

,ω

The Euler equations in this instance are

˙ω

+ (I

− I

)ω

= 0 (3.228)

˙ω

− (I

− I

)ω

= 0 (3.229)

˙ω

+ (I

− I

)ω

= M

(3.230)

Since ω

and ω

are small, (3.228) can be approximated by ˙ω

= 0or

=  (3.231)

where  is a constant. Then a differentiation of (3.229) with respect to time results in

¨ω

− I

 ˙ω

(3.232)

where, from (3.230),

˙ω

=−

− I

ω

(3.233)

Thus we obtain

¨ω

− I

)(I

− I

)



− I

M

(3.234)

176 Kinematics and dynamics of a rigid body

The solution of this linear differential equation has the form

= C

cos λt +C

sin λt +

− I

)

(3.235)

where the natural frequency is

λ =



− I

)(I

− I

)

 (3.236)

Then, from (3.229),

− I

)

˙ω

− I

)

cos λt −C

sin λt) (3.237)

As a speciﬁc example, let us assume the initial conditions ω

(0) = ω

(0) = 0. Then

=−

− I

)

, C

= 0 (3.238)

and we obtain the solutions

− I

)

(

1 −cos λt

)

(3.239)

sin λt (3.240)

Since  and λ are large, we see that ω

and ω

are small, in agreement with the earlier

assumption.

It is perhaps surprising that a constant applied moment about the z-axis produces an ω

which is periodic with average value zero rather than constantly increasing. A plot of ω

versus ω

is elliptical with its center on the ω

axis. Furthermore, notice from (3.236) that

if I

is the intermediate principal moment of inertia, then the solutions for ω

and ω

are

no longer sinusoidal and they do not remain small.

Lagrange’s equations

The various forms of Lagrange’s equations such as (2.34), (2.37) and (2.49) are all useful

in obtaining equations of motion for a system involving one or more rigid bodies. There are

restrictions, however, on the use of Lagrange’s equations.

The ﬁrst restriction is that a complete set of qs and

qs must be used in writing the energy

functions T and V . This means that the chosen set of generalized coordinates must be able

to specify the conﬁguration of the system, thereby specifying the locations of all particles

and mass elements of the system.

177 Basic rigid body dynamics

As an example, suppose we wish to use type I Euler angles as generalized coordinates in

the Lagrangian analysis of the rotational motion of an axially-symmetric body having no

applied moment about the axis of symmetry. The rotational kinetic energy can be written

in the form

T =



(

cos

θ) (3.241)

where the moments of inertia are taken about the center of mass and the total spin  is

constant. Let us apply Lagrange’s equation in the fundamental form



∂T

∂



−

∂T

∂q

= Q

(3.242)

where the qs are the Euler angles (ψ, θ, φ). If we assume that neither Q

nor Q

are

functions of φ or

φ, then it appears that the ψ and θ equations can be solved separately,

treating  as a constant in the differentiations, and effectively reducing the number of

degrees of freedom to two.

This application of Lagrange’s equation would be incorrect, however, because the system

actually has three rotational degrees of freedom, but the third Euler angle φ has not entered

the analysis. Thus, we have not used a complete set of generalized coordinates. A correct

approach would be to substitute

 =

φ −

ψ sin θ (3.243)

into (3.241) and obtain

T =

(

φ −

ψ sin θ )

(

cos

θ) (3.244)

The use of this kinetic energy function in Lagrange’s equation (3.242) leads to correct

equations of motion. An alternate approach would be to notice that φ is an ignorable

coordinate and use the Routhian method.

The second restriction on the use of Lagrange’s equation in a form such as (3.242) is

that true

qs must be used in writing the kinetic energy T (q,

q, t), rather than using quasi-

velocities as velocity variables. A quasi-velocity u

is equal to a linear function of the

and has the form



i=1



(q, t)

+ 

(q, t)(j = 1,...,n) (3.245)

where the right-hand side is not integrable.

A common example of quasi-velocities would be the body-axis components ω

,ω

the angular velocity ω of a rigid body. In terms of Euler angles, which are true coordinates,

we have

φ −

ψ sin θ

ψ cos θ sin φ +

θ cos φ (3.246)

ψ cos θ cos φ −

θ sin φ

178 Kinematics and dynamics of a rigid body

and we see that the right-hand sides are not integrable. Assuming principal axes, the kinetic

energy due to rotation about the center of mass of a rigid body is

T =

(3.247)

However, a substitution into Lagrange’s equation (3.242), treating the ωsas

qs, does not

result in correct equations of motion. Terms are missing. Thus, the correct Euler equations

of motion are not obtained by using Lagrange’s equation. It is possible, however, to expand

the Lagrange formulation to include the required terms. This is a topic to be discussed in

the next chapter.

Example 3.6 Let us obtain the differential equations for the rotational motion of a rigid

body, using type I Euler angles as generalized coordinates. We choose the center of mass as

the reference point and thereby decouple the translational and rotational motions. Assume

a principal axis system and arbitrary applied moments.

The rotational kinetic energy is found by substituting from (3.246) into (3.247) with the

result that

T =

(

φ −

ψ sin θ )

(

ψ cos θ sin φ +

θ cos φ)

(

ψ cos θ cos φ −

θ sin φ)

(3.248)

The generalized momenta are

∂T

∂

= [I

sin

θ + (I

sin

φ + I

cos

φ) cos

θ]

+[(I

− I

) cos θ sin φ cos φ]

θ − I

φ sin θ

∂T

∂

= (I

− I

)

ψ cos θ sin φ cos φ + (I

cos

φ + I

sin

φ)

θ (3.249)

∂T

∂

= I

(

φ −

ψ sin θ )

These equations have the matrix form

p = m

q (3.250)

where the mass or inertia matrix is

m =







sin

θ + (I

sin

+ I

cos

φ) cos

θ]

− I

) cos θ sin φ cos φ −I

sin θ

− I

) cos θ sin φ cos φ I

cos

φ + I

sin

φ 0

−I

sin θ 0 I







(3.251)

for the order (ψ, θ, φ).