Greenwood D.T. Advanced Dynamics

Подождите немного. Документ загружается.

139 Problems

Figure P 2.21.

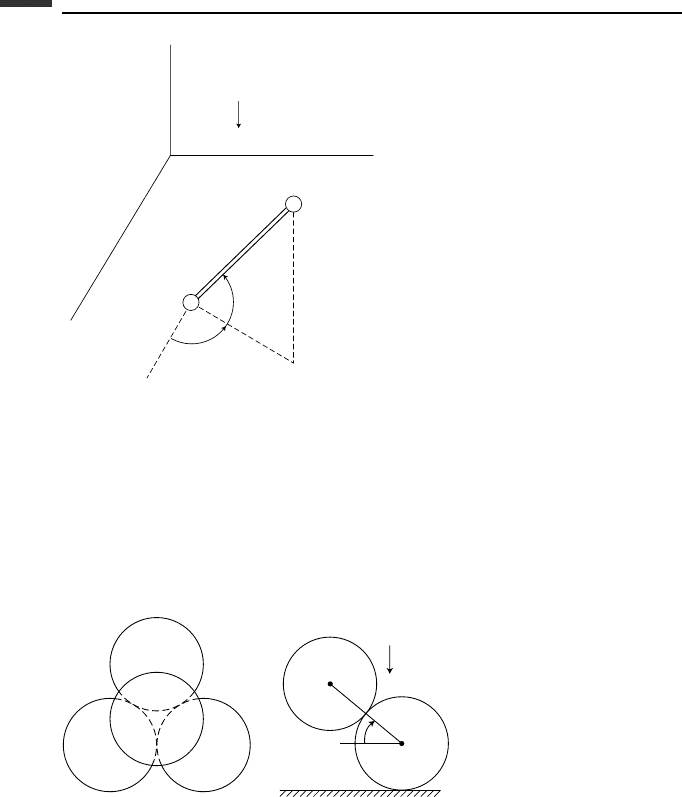
2.22. Four frictionless uniform spheres, each of mass m and radius r , are placed in the

form of a pyramid on a horizontal surface. They are released from rest with the upper

sphere moving downward and the lower spheres moving radially outward without

rotation. Because of the symmetry, the angle θ to the top sphere is the same for all

three lower spheres. (a) Find the differential equation for θ, assuming that sphere

1 remains in contact with the lower spheres. (b) Find the angle θ at which the top

sphere loses contact with the others. (c) What is the ﬁnal velocity of sphere 2?

side view

top view

Figure P 2.22.

Kinematics and dynamics of a rigid body

A rigid body may be viewed as a special case of a system of particles in which the particles

are rigidly interconnected with each other. As a consequence, the basic principles which

apply to systems of particles also apply to rigid bodies. However, there are additional

kinematical and dynamical formulations which are speciﬁcally associated with rigid bodies,

and which contribute greatly to their analysis. This chapter will be primarily concerned with

a discussion of these topics.

3.1 Kinematical preliminaries

Degrees of freedom

The conﬁguration of a rigid body can be expressed by giving the location of an arbitrary point

in the body and also giving the orientation of the body in space. This can be accomplished

by ﬁrst considering a Cartesian body-axis frame to be ﬁxed in the rigid body with its origin

at the arbitrary reference point for the body. The location of the origin of this xyz body-axis

frame can be given by the values of three Cartesian coordinates relative to an inertial XYZ

frame. The orientation of the rigid body is speciﬁed by giving the orientation of the body

axes relative to the inertial frame. This relative orientation is frequently expressed in terms

of three independent Euler angles which will be deﬁned.

The number of degrees of freedom of a rigid body is equal to the number of independent

parameters required to specify its conﬁguration which, in effect, speciﬁes the locations of all

the particles comprising the body. In this case, there are three Cartesian coordinates and three

Euler angles, so there are six degrees of freedom for the rigid body. Alternative methods are

available for specifying the orientation, but in each case the number of parameters minus the

number of independent constraining relationships is equal to three, the number of degrees of

freedom associated with orientation. To summarize, a rigid body has six degrees of freedom,

three being translational and three rotational.

Rotation of axes

Let r be an arbitrary vector. We seek a relationship between its components in the primed

and unprimed coordinate systems of Fig. 3.1. This relationship must be linear, so we can

141 Kinematical preliminaries

z′

y′

x′

Figure 3.1.

write the matrix equation



= Cr (3.1)

In detail, we have





























(3.2)

where

r = xi + yj + zk = x



+ y



+ z



(3.3)

The matrix C is called a rotation matrix and it speciﬁes the relative orientation of the two

coordinate systems. An element c



is equal to the cosine of the angle between the positive



and j axes, and is called a direction cosine. By convention, the ﬁrst subscript refers to the

ﬁnal coordinate system, and the second subscript refers to the original coordinate system.

In order to transform a given set of components to a new coordinate system, premultiply by

the corresponding rotation matrix.

In general, the nine elements of a rotation matrix are all different. The ﬁrst column of the

C matrix gives the components of the unit vector i in the primed frame. Similarly, the second

142 Kinematics and dynamics of a rigid body

and third columns of C represent j and k respectively, in the primed frame. Hence, the sum

of the squares of the elements of a single column must equal one. In other words, the scalar

product of a unit vector with itself must equal one. On the other hand, the scalar product of

any two different columns must equal zero, since the unit vectors are mutually orthogonal.

Altogether, there are three independent equations for single columns, and three independent

equations for pairs of columns, giving a total of six independent constraining equations. The

number of direction cosines (nine) minus the number of independent constraining equations

(six) yields three, the number of rotational degrees of freedom.

By interchanging primed and unprimed subscripts, we see that the transposed rotation

matrix C

is the rotation matrix for the transformation from the primed frame to the unprimed

frame. Hence, the sequence of transformations C and C

, in either order, will return a

coordinate frame to its original orientation. We ﬁnd that

r = C



(3.4)

and, using (3.1) and (3.4),

C = CC

= U (3.5)

where U is a 3 × 3 unit matrix, that is, with ones on the main diagonal and zeros elsewhere.

From (3.5) it is apparent that

= C

−1

(3.6)

Matrices such as the rotation matrix whose transpose and inverse are equal are classed as

orthogonal matrices. The determinant of any rotation matrix is equal to +1.

In general, a rotation of axes given by C

followed by a second rotation C

is equivalent

to a single rotation

C = C

(3.7)

The order of matrix multiplications is important, indicating that the order of the correspond-

ing ﬁnite rotations is also important. As we shall see, the deﬁnitions of the various Euler

angle systems used in specifying rigid body orientations always require a particular order

in making the rotations.

Euler angles

The rotation of a rigid body from some reference orientation to an arbitrary ﬁnal orientation

can always be accomplished by three rotations in a given sequence about speciﬁed body

axes. The resulting angles of rotation are known as Euler angles. Many Euler angle systems

are possible, but we will consider only two, namely, aircraft Euler angles and classical Euler

angles.

Type I (aircraft) Euler angles are shown in Fig. 3.2 and represent an axis-of-rotation

order zyx, where each successive rotation is about the latest position of the given body

axis. Assume that the xyz body axes and the XYZ inertial axes coincide initially. Then three

143 Kinematical preliminaries

x′′, x

y′, y′′

x′

Line of nodes

z′′

Z, z′

Figure 3.2.

rotations are made in the following order: (1) ψ about the Z -axis, resulting in the primed

axis system; (2) θ about the y



-axis (line of nodes) resulting in the double-primed system;

(3) φ about the x



-axis, resulting in the ﬁnal xyz body-ﬁxed frame.

Incremental changes in the Euler angles are indicated by the corresponding angular

velocity vectors; namely,

ψ about the Z -axis,

θ about the y



-axis (line of nodes), and

about the x -axis. The absolute angular velocity of the xyz body-axis frame is

ω =

ψ +

θ +

φ (3.8)

Note that the vectors

ψ and

φ are not orthogonal. In terms of body-axis components,

ω = ω

i + ω

j + ω

k (3.9)

For an aircraft, ω

is the roll rate, ω

is the pitch rate, and ω

is the yaw rate. A rotation

matrix C, deﬁned in terms of direction cosines, was given by (3.2). For rotations about

individual Cartesian axes, we have the following results. A rotation φ about the x-axis is

144 Kinematics and dynamics of a rigid body

represented by the matrix

 =





10 0

0 cos φ sin φ

0 −sin φ cos φ





(3.10)

A rotation θ about the y-axis is

 =





cos θ 0 −sin θ

01 0

sin θ 0 cos θ





(3.11)

A rotation ψ about the z-axis is

 =





cos ψ sin ψ 0

−sin ψ cos ψ 0

001





(3.12)

Noting that successive rotations are represented by successive premultiplications by the

corresponding rotation matrices, the overall rotation matrix for type I Euler angles is

C =  (3.13)

or, in detail,

C =







cos ψ cos θ sin ψ cos θ −sin θ

(−sin ψ cos φ

+cos ψ sin θ sin φ)

(cos ψ cos φ

+sin ψ sin θ sin φ)

cos θ sin φ

(sin ψ sin φ

+cos ψ sin θ cos φ)

(−cos ψ sin φ

+sin ψ sin θ cos φ)

cos θ cos φ







(3.14)

Usually, we consider that the ranges of the Euler angles are

0 ≤ ψ<2π, −

≤ θ ≤

, 0 ≤ φ<2π

The body-axis components of the absolute angular velocity in terms of Euler angle rates

are

φ −

ψ sin θ

ψ cos θ sin φ +

θ cos φ (3.15)

ψ cos θ cos φ −

θ sin φ

Conversely, the Euler angle rates in terms of angular velocity components are

ψ = sec θ (ω

sin φ + ω

cos φ)

θ = ω

cos φ − ω

sin φ

(3.16)

φ = ω

ψ sin θ

= ω

+ ω

tan θ sin φ + ω

tan θ cos φ

145 Kinematical preliminaries

We see from (3.15) that ω

, ω

are well-deﬁned for arbitrary Euler angles and Euler

angle rates. But if θ =±π/2, equation (3.16) shows that

ψ and

φ can be inﬁnite even if

ω is ﬁnite. Furthermore, the angles ψ and φ are not well-deﬁned if the x -axisofFig.3.2

points vertically upward or downward in this singular situation. If θ = π/2, for example,

ψ and φ are undeﬁned, but (ψ − φ) is the angle between the Y and y axes.

All types of Euler angle systems are subject to singularity problems which occur when

two of the Euler angle rates represent rotations about the same axis in space. Thus, in

Fig. 3.2 the

ψ and

φ rotations occur about the same vertical axis if θ =±π/2. When

combined with a

θ rotation about a horizontal axis, this limits the ω vector to a deﬁnite

vertical plane when using this Euler angle representation, even though the actual motion

may have no such constraint. For these reasons and the associated problems of maintain-

ing accuracy in numerical computations, it is the usual practice to choose an Euler angle

system such that the rotational motion of the rigid body does not come near a singular

orientation.

Type II Euler angles are shown in Fig. 3.3. The order of rotation is as follows: (1) φ about

the Z-axis; (2) θ about the x



-axis; (3) ψ about the z



-axis. The usual ranges of the Euler

angles are

0 ≤ φ<2π, 0 ≤ θ ≤ π, 0 ≤ ψ<2π

y′′

y′

x′, x′′

z′′, z

Line of nodes

Z, z′

Figure 3.3.

146 Kinematics and dynamics of a rigid body

The absolute angular velocity of the xyz frame is

ω =

φ +

θ +

ψ (3.17)

with the body-axis components

φ sin θ sin ψ +

θ cos ψ

φ sin θ cos ψ −

θ sin ψ (3.18)

ψ +

φ cos θ

Conversely, we obtain

φ = csc θ (ω

sin ψ + ω

cos ψ)

θ = ω

cos ψ − ω

sin ψ (3.19)

ψ = ω

−

φ cos θ

=−ω

cot θ sin ψ − ω

cot θ cos ψ + ω

Singular orientations of the body occur for θ = 0orπ, and both

φ and

ψ become inﬁnite

even with ﬁnite ω

and ω

. Furthermore, we note that the

φ and

ψ rotations occur about

the same vertical axis in Fig. 3.3.

The overall rotation matrix for Type II Euler angles is

C =  (3.20)

where

 =





cos φ sin φ 0

−sin φ cos φ 0

001





(3.21)

 =





10 0

0 cos θ sin θ

0 −sin θ cos θ





(3.22)

 =





cos ψ sin ψ 0

−sin ψ cos ψ 0

001





(3.23)

In detail, we obtain

C =







(cos φ cos ψ

−sin φ cos θ sin ψ)

(sin φ cos ψ

+cos φ cos θ sin ψ)

sin θ sin ψ

(−cos φ sin ψ

−sin φ cos θ cos ψ)

(−sin φ sin ψ

+cos φ cos θ cos ψ)

sin θ cos ψ

sin φ sin θ −cos φ sin θ cos θ







(3.24)

147 Kinematical preliminaries

Euler angles are true generalized coordinates and, as such, can be used as qs in Lagrange’s

equations. We shall ﬁnd, however, that other methods may be more convenient in obtaining

the dynamical equations for the rotational motion of a rigid body.

Axis and angle of rotation

An important result in rigid body kinematics is expressed by Euler’s Theorem: The most

general displacement of a rigid body with a ﬁxed point is equivalent to a single rotation

about some axis through that point.

Because a ﬁxed point is assumed, any motion involves a change of orientation. Hence,

Euler’s theorem is concerned with orientation changes. On the basis of this theorem, we

conclude that, although any Euler angle system expresses an orientation change in terms of

a sequence of three rotations about coordinate axes, the same change of orientation could

have been obtained by a single rotation about a ﬁxed axis. Hence, if one can specify the

direction of the axis of rotation, as well as the angle of rotation about this axis, it is equivalent

to specifying three Euler angles or a rotation matrix consisting of nine direction cosines.

Suppose we let the direction of the axis of rotation be given by the unit vector

a = a

i + a

j + a

k (3.25)

where i, j, k are Cartesian unit vectors and the scalar as are constrained by the relation

+ a

= 1 (3.26)

These ashavethesame values in either the inertial or the body-ﬁxed frame, and remain

constant during the rotation because the rotation axis is ﬁxed in both frames. Let φ be the

angle of rotation of the body-ﬁxed frame relative to the inertial frame, where positive φ is

measured in a right-hand sense about the unit vector a. The values of the four parameters

, a

,φ) specify the orientation of the rigid body and its body-ﬁxed frame. These are

the axis and angle variables.

Now suppose that we are given a rotation matrix C and we desire the corresponding

values of the axis and angle variables. First, the angle of rotation φ is found from the trace

of the rotation matrix, that is,

tr C = c

+ c

= 1 + 2 cos φ, 0 ≤ φ ≤ π (3.27)

Then, knowing φ, we can ﬁnd the direction cosines of the axis of rotation from

− c

2 sin φ

− c

2 sin φ

(3.28)

− c

2 sin φ

For convenience, the primes have been dropped from the subscripts of the cs. Note that

the limits on φ given in (3.27) imply that sin φ is positive or zero. This is always possible

148 Kinematics and dynamics of a rigid body

because a rotation φ is equivalent to a rotation (2π − φ) about an oppositely directed

a axis.

If the value of φ is near 0 or π, then |sin φ| << 1 and (3.28) leads to inaccurate results.

In this case, better accuracy can be obtained by using

− c

)

− c

) (3.29)

− c

)

where

d = [(c

− c

)

+ (c

− c

)

+ (c

− c

)

]

A comparison of (3.28) and (3.29) shows that

sin φ =

d (3.30)

For values of φ near 0 or π , this equation is more accurate than (3.27) in determining φ.

Note that (3.27) uses the main diagonal terms of C to evaluate φ, whereas (3.30) uses the

off-diagonal terms. For these small positive values of sin φ, (3.27) is used to determine the

quadrant.

Now consider the case in which the axis and angle variables are given, and we wish to

ﬁnd the corresponding rotation matrix. First, let us write the rotation matrix C as the sum

of its symmetric and antisymmetric parts.

C = C

+ C

(3.31)

The symmetric matrix is

(C +C

) (3.32)

and the antisymmetric (or skew-symmetric) matrix is

(C −C

) (3.33)

It can be shown that, in terms of axis and angle variables, the symmetric portion of the

rotation matrix is

= cos φ U + (1 − cos φ)aa

(3.34)

or, in detail,

= cos φ







100

010

001







+ (1 − cos φ)













(3.35)