Greenwood D.T. Advanced Dynamics

Подождите немного. Документ загружается.

109 Dissipative and gyroscopic forces

–

cone of

friction

Figure 2.10.

where the coefﬁcient of

θ is equal to the distance from C to the particle.

The kinetic energy is

T =



+ cos θ



(2.267)

The potential energy is

V = mg



−rθ sin α +

r cos(θ + α)



= mgr



−

θ +

√

cos θ −

sin θ



(2.268)

We ﬁnd that



∂T

∂



= mr



+ cos θ



− mr

sin θ (2.269)

∂T

∂θ

=−

sin θ (2.270)

∂V

∂θ

=−mgr



√

sin θ +

cos θ



(2.271)

From (2.265) the differential equation of motion, assuming no slipping, is found to be



+ cos θ



−

sin θ − mgr



√

sin θ +

cos θ



= 0 (2.272)

110 Lagrange’s and Hamilton’s equations

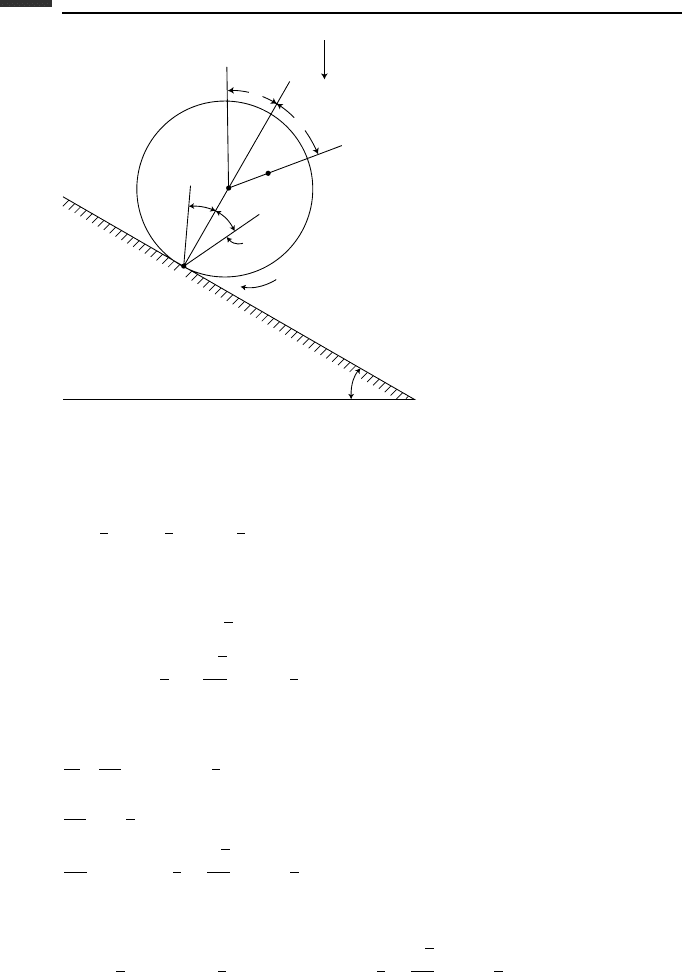
The angle θ at which slipping begins can be obtained directly by using the cone of friction.

First, note that since the disk is massless there is no resistance to angular acceleration about

the particle. Hence, there can be no applied moment about the particle. This means that the

line of action of the force at the contact point C must pass through the particle. If this line

of action lies within the cone of friction, there is no slipping. But slipping begins when θ

reaches 90

◦

, at which time

tan φ =

= µ (2.273)

and the particle lies on the cone of friction.

Slipping will continue as long as the particle is outside the cone of friction but will end

when it re-enters the cone at

θ = 90

◦

+ 2φ = 143.1

◦

(2.274)

During the period when the particle is outside the cone of friction, the force at C must drop

to zero since the line of action of any force must pass through the particle and lie on or

within that cone. Thus, the particle moves in free fall under the action of gravity during the

slipping period, and continuously approaches the inclined plane. It is reasonable to assume

that the disk maintains contact with the plane during the free fall of the particle since

θ is

continuously positive and one might consider the effect of an inﬁnitesimal rotational inertia

about the particle.

At the instant when the particle re-enters the cone of friction, the sliding suddenly stops

and the particle velocity must be perpendicular to the cone of friction. This means that an

impulse must be applied to the particle to cause a sudden change in velocity, namely, the

velocity component toward C due to sliding must be canceled. Finally, notice that the range

of values of θ over which slipping occurs turns out to be independent of the inclination

angle α.

2.5 Conﬁguration space and phase space

Conﬁguration space

In Chapter 1 we introduced the idea of conﬁguration space. We deﬁned the conﬁguration

of a system to be speciﬁed by the values of its n generalized coordinates. Thus, at any given

time, the conﬁguration is represented by a conﬁguration point C having a position vector q

in an n-dimensional conﬁguration space or q-space. As time proceeds, the point C traces

a solution path or trajectory in conﬁguration space (Fig. 1.19).

If the system has m holonomic constraints of the form

(q, t) = 0(j = 1,...,m) (2.275)

each constraint is represented by a surface in conﬁguration space on which the conﬁguration

point C must move. Thus, for m independent holonomic constraints, the point C is conﬁned

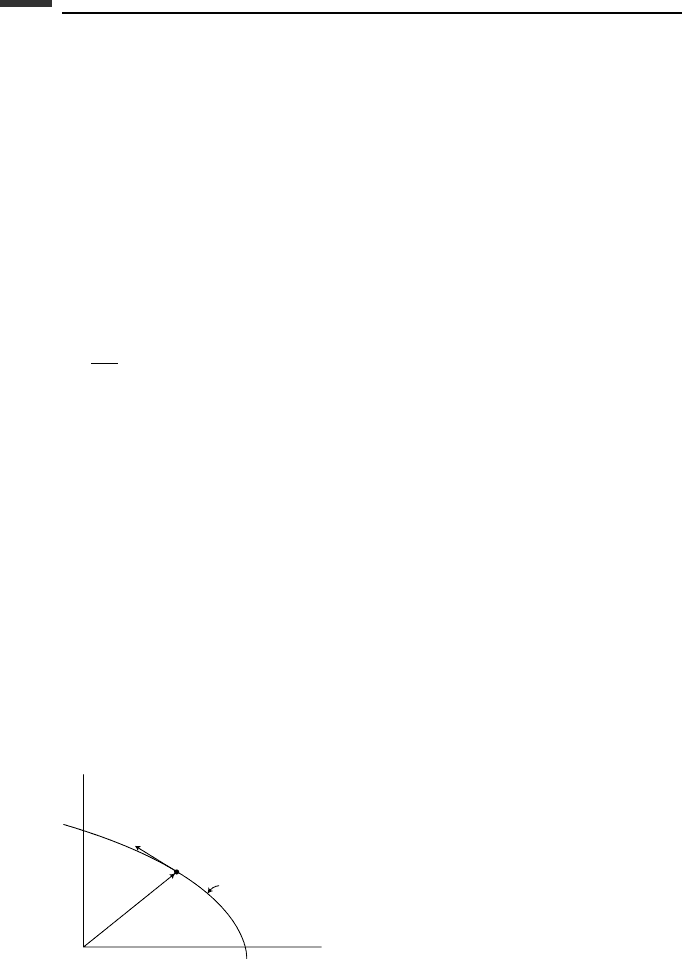
111 Conﬁguration space and phase space

to the common intersection of these surfaces, which is itself a subspace of (n − m) dimen-

sions. In general, the constraint surfaces are moving, but they are ﬁxed if the constraints are

scleronomic of the form φ

(q).

It is always possible to give the location of C within the constraint intersection subspace

by deﬁning (n − m) new generalized coordinates which are independent and specify the

conﬁguration of the system. In other words, it is always possible, in theory, to ﬁnd a set of

(n − m) independent generalized coordinates which are consistent with the constraints and

deﬁne the conﬁguration of a holonomic system. These independent qs can then be used in

writing equations of motion by means of Lagrange’s equations.

A virtual displacement δq which is consistent with the holonomic constraint

,...,q

, t) = 0 (2.276)

must satisfy the instantaneous constraint equation



i=1

∂φ

∂q

δq

= 0 (2.277)

The coefﬁcients of ∂φ

/∂q

are components of the gradient vector which is perpendicular

to the constraint surface. Equation (2.277) states that the dot product of the gradient vector

and δq in conﬁguration space is equal to zero. Hence, the two vectors are orthogonal and

δq must lie in the tangent plane at the operating point C (Fig. 2.11).

Now let us suppose there are m nonholonomic constraints acting on the system. The

constraints have the general form

(q,

q, t) = 0(j = 1,...,m) (2.278)

or, in the usual linear case,



i=1

(q, t)

+ a

(q, t) = 0(j = 1,...,m) (2.279)

There are no constraint surfaces in conﬁguration space because the constraint equations

are not integrable. Since there are no constraint surfaces, the entire n-dimensional space

is accessible to the conﬁguration point C. We see that nonholonomic constraints, for any

(q, t) = 0

δq

Figure 2.11.

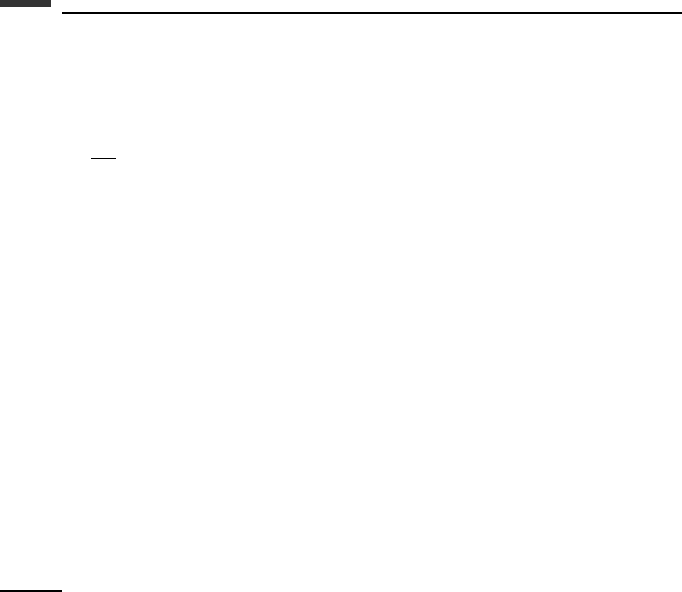
112 Lagrange’s and Hamilton’s equations

given conﬁguration and time, are essentially restrictions on the possible velocities of the

system. For the common case of catastatic constraints (a

= 0), the restrictions are on the

possible directions of

q rather than on its magnitude.

Any virtual displacements of a nonholonomic system must satisfy the Chetaev equation



i=1

∂ f

∂

δq

= 0(j = 1,...,m) (2.280)

or, more commonly,



i=1

(q, t)δq

= 0(j = 1,...,m) (2.281)

which is the instantaneous or virtual constraint equation. The coefﬁcients a

represent

components of a vector associated with the j th constraint and which is normal to the

differential surface in which any virtual displacement δq must lie. By properly steering

the conﬁguration point C and its associated (n − m)-dimensional differential surface, it is

always kinematically possible to go between any two points of conﬁguration space if all

the constraints are nonholonomic and there are at least two degrees of freedom.

It is sometimes convenient to represent solution paths in an extended conﬁguration space

or event space of n + 1 dimensions consisting of the nqs and time. In this space, a solution

path will never cross itself. Also, constraint surfaces corresponding to rheonomic holonomic

constraints will be ﬁxed rather than moving. When one considers variational methods in

dynamics, some procedures are more easily visualized in extended conﬁguration space.

Phase space

We have seen that Lagrange’s equations for a dynamical system are n second-order differ-

ential equations whose solutions q

(t) are conveniently expressed as paths in conﬁguration

space. For a given dynamical system, there is more than one possible path through a given

conﬁguration point because of the variety of possible velocities.

Now consider Hamilton’s canonical equations for a holonomic system. They are 2n ﬁrst-

order differential equations giving

qs and

ps as functions of (q, p, t ). We can consider the

qs and ps together to form a 2n-vector x = (q

,...,q

, p

,..., p

) and then the equations

of motion have the form

= X

(x , t )(i = 1,...,2n) (2.282)

The motion of the system can be represented by the path of a phase point P moving in

the 2n-dimensional phase space. Note that a point in phase space speciﬁes not only the

conﬁguration but also the state of motion as represented by the ps.

Phase space is particularly convenient in presenting the possible motions of a conservative

holonomic system. In this case the Hamiltonian function is not an explicit function of time,

and the equations of motion have the form

= X

(x )(i = 1,...,2n) (2.283)

113 Conﬁguration space and phase space

or, in detail,

∂ H (q, p)

∂p

=−

∂ H (q, p)

∂q

(i = 1,...,2n) (2.284)

Because the system is conservative the Hamiltonian function is constant, that is

H(q, p) = h (2.285)

where h is usually evaluated from the initial conditions. This equation represents a surface

in phase space, and the corresponding trajectory must lie entirely on this surface. From

(2.283) or (2.284) we see that the direction of motion is given at all ordinary points where

the velocity is not zero. Hence, there is only one trajectory through each point, and every

trajectory is ﬁxed. Thus, the whole of phase space with its trajectories represents the totality

of all possible motions of a conservative system.

A point in phase space at which all the

qs and

ps are zero is known as an equilibrium point

or singular point. The corresponding trajectory consists of the equilibrium point only. If we

make the usual assumption that the Hamiltonian function has at least two partial derivatives

with respect to the qs and ps, it can be shown that an inﬁnite time is required to enter or

leave an equilibrium point. Thus, although more than one trajectory may apparently pass

through an equilibrium point, it cannot do so in a ﬁnite time.

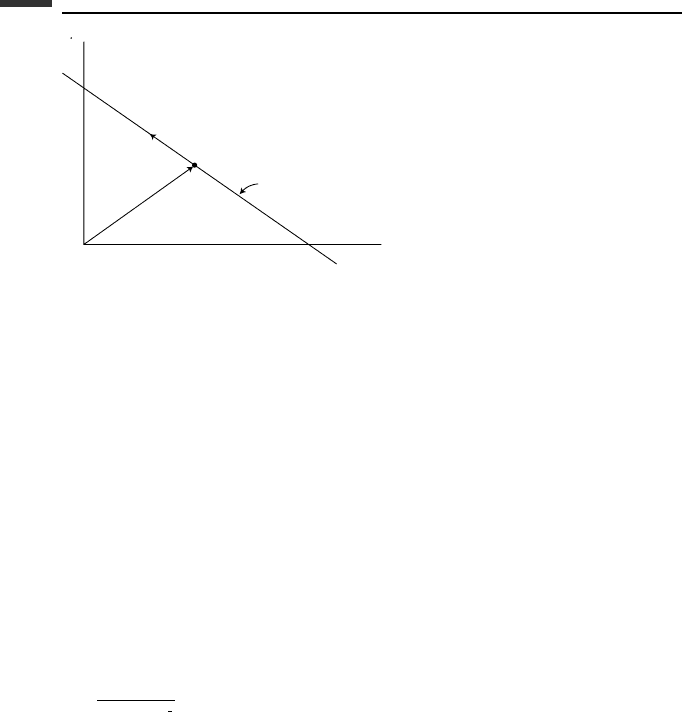
As a simple example of phase space methods, consider the phase plane diagram of

Fig. 2.12 which shows the possible solution paths in qp-space for a simple pendulum. Here

q is the pendulum angle and p is the corresponding angular momentum. There is a position

of stable equilibrium at A, corresponding to θ = 0. Points B and C represent unstable

equilibrium positions at θ =±π.

Now suppose that solution curves are traced in a 2n-dimensional state space consisting

of the nqs and n

qs. If one knows the state of a system at a certain initial time t

, then the

differential equations will determine its further motion. This is equivalent to knowing the

Figure 2.12.

114 Lagrange’s and Hamilton’s equations

initial values of the qs and ps in phase space. Thus, the trajectories in state space are similar

to those in phase space. In particular, the equilibrium points of conservative holonomic

systems occur at the same values of qs in both spaces.

Velocity space

The concept of velocity space is important in the analysis of nonholonomic systems. Non-

holonomic constraints are essentially constraints on the velocities (

qs) of a system for a

given conﬁguration and time, whereas holonomic constraints restrict the possible conﬁgu-

rations (qs) at a given time. Thus, the role of

qs for nonholonomic constraints is similar to

that of qs for holonomic constraints.

Velocity space is the n-dimensional space of the

qs. Nonholonomic constraints can be

represented as surfaces in velocity space, where the qs and t are regarded as parameters.

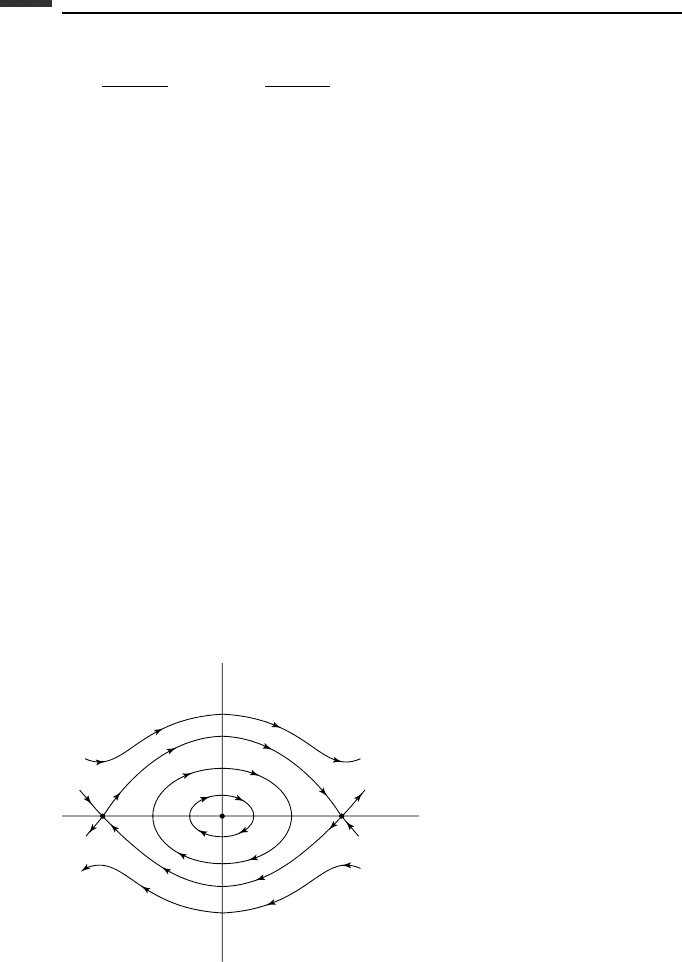
For example, consider a general nonholonomic constraint of the form

(q,

q, t) = 0 (2.286)

which is represented as a curved surface in velocity space (Fig. 2.13).

The constraint force C

is perpendicular to the constraint surface; that is, its components

are proportional to ∂ f

/∂

(i = 1,...,n) which are the components of the gradient vector

in velocity space. A virtual velocity vector δw must lie in the tangent plane at the operating

point P. Therefore, δw and C

are orthogonal, implying that



i=1

δw

= 0 (2.287)

similar to a virtual work expression, or



i=1

∂ f

∂

δw

= 0 (2.288)

δw

(q, q, t) = 0

Figure 2.13.

115 Conﬁguration space and phase space

δw

constraint

plane

Figure 2.14.

Comparing (2.288) with the Chetaev expression of (2.280) for virtual displacements, we

see that the virtual velocity vector δw and the virtual displacement vector δq are constrained

to the same allowable directions in space.

Now consider the common case where there are nonholonomic constraints of the linear

form



i=1

(q, t)

+ a

(q, t) = 0(j = 1,...,m) (2.289)

Each constraint is represented by a plane in velocity space (Fig. 2.14). The virtual velocity

δw can be considered as a variation δ

q with q and t ﬁxed, and must satisfy



i=1

(q, t)δw

= 0(j = 1,...,m) (2.290)

Therefore, it must lie in the (n − m)-dimensional intersection of the constraint planes.

The distance d from the origin of a constraint plane in velocity space is

d =







(2.291)

We see that if the nonholonomic constraint is catastatic (a

= 0), then the constraint plane

goes through the origin. In this case, if a velocity

q satisﬁes the constraints, then

q multiplied

by an arbitrary scalar constant also satisﬁes the constraints. Thus, for the rather common

case of catastatic constraints, the effect of nonholonomic constraints on a system is to

restrict the possible directions of

q but not its magnitude.

When one considers conservative systems which also have catastatic nonholonomic con-

straints, there is a temptation to consider the energy integral as an additional nonholonomic

constraint. There are, however, qualitative differences between ordinary kinematic con-

straints and energy constraints. For a given conﬁguration and time, an energy constraint is

actually a constraint on the kinetic energy, and is represented in velocity space by a closed

116 Lagrange’s and Hamilton’s equations

surface which surrounds the origin. This means that an energy constraint does not restrict

the direction of

q, but for any given direction, its magnitude is speciﬁed. On the other hand,

we found that linear catastatic constraints restrict the possible directions of

q but not the

magnitude.

As a natural application of velocity space methods, let us consider the derivation of

Jourdain’s principle. We start with Lagrange’s principle as expressed in (2.33), namely,



i=1





∂T

∂



−

∂T

∂q

− Q



δq

= 0 (2.292)

where the δqs satisfy the instantaneous constraints expressed in (2.280) or (2.281).

Lagrange’s principle applies to holonomic or nonholonomic systems and leads to (n − m)

differential equations of motion if there are m constraints. A comparison of (2.281) which

constrains the δqs in conﬁguration space with (2.290) which constrains the δws in velocity

space shows that the corresponding δqs and δws are proportional. Hence, we can substitute

δw

for δq

in (2.292). We obtain



i=1





∂T

∂



−

∂T

∂q

− Q



δw

= 0 (2.293)

This is Jourdain’s principle. The variation δw is considered to take place in velocity space

at an operating point P on the common intersection of the constraint planes. By choosing

(n − m) independent sets of δws which satisfy the constraints expressed in (2.290), one can

use Jourdain’s principle to obtain (n − m) second-order differential equations of motion.

In addition, there are m constraint equations, making a total of n equations to solve for the

nqs.

Example 2.12 Let us apply Jourdain’s principle to the nonholonomic system (Fig. 2.3)

which was studied previously in Example 2.3 on page 83. The conﬁguration of a dumbbell

that moves in the horizontal xy-plane is given by the generalized coordinates (x, y,φ).

There is a knife-edge constraint at particle 1 which has the Cartesian coordinates (x, y),

and the relative position of particle 2 with respect to particle 1 is given by the angle φ.

The nonholonomic constraint equation is

−

x sin φ +

y cos φ = 0 (2.294)

which states that the velocity of particle 1 is limited to the longitudinal direction. Hence,

the virtual velocity components must satisfy

−sinφδw

+ cos φδw

= 0 (2.295)

where δw

≡ δ

x and δw

≡ δ

y. The kinetic energy of the unconstrained system is

T = m



−l

φ sin φ + l

φ cos φ



(2.296)

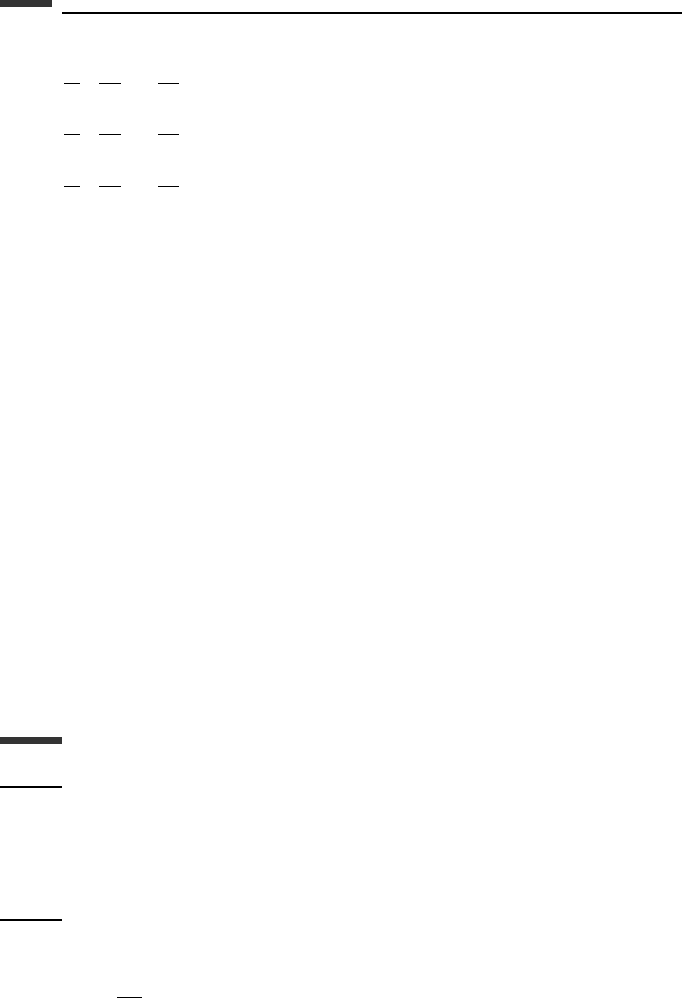
117 Impulse response, analytical methods

and we obtain



∂T

∂



−

∂T

∂x

= m(2

x −l

φ sin φ − l

cos φ) (2.297)



∂T

∂



−

∂T

∂y

= m(2

y +l

φ cos φ − l

sin φ) (2.298)



∂T

∂



−

∂T

∂φ

= ml(−

x sin φ +

y cos φ + l

φ) (2.299)

In this example, n = 3 and m = 1 so there are two independent sets of δws which satisfy

(2.295). We can choose

δw = (cos φ,sin φ,0) (2.300)

and

δw = (0, 0, 1) (2.301)

Notice that these components of δw are not necessarily inﬁnitesimal.

Using Jourdain’s principle and the ﬁrst set of δws, we obtain

m(2

x cos φ + 2

y sin φ − l

) = 0 (2.302)

which is the ﬁrst equation of motion. The second equation of motion is obtained by using

the second set of δws, resulting in

ml(−

x sin φ +

y cos φ + l

φ) = 0 (2.303)

These differential equations of motion are the same as those obtained by ﬁrst using

the nonholonomic Lagrange equations with Lagrange multipliers, and then algebraically

eliminating the λs. However, the use of Jourdain’s principle appears to be more direct.

In addition to the two equations of motion, (2.302) and (2.303), a third equation is obtained

by differentiating the constraint equation with respect to time, with the result

−

x sin φ +

y cos φ −

φ cos φ −

φ sin φ = 0 (2.304)

These three equations are sufﬁcient to solve for x (t ), y(t), and φ(t).

2.6 Impulse response, analytical methods

In the previous discussion of impulse methods in Chapter 1, Newton’s law and vectorial

methods were used. In this chapter we will use the analytical methods of Hamilton and

Lagrange, and will pay particular attention to constrained systems.

Hamiltonian approach

Consider an unconstrained system whose dynamical equation of motion has the Hamiltonian

form

=−

∂ H

∂q

+ Q



(i = 1,...,n) (2.305)

118 Lagrange’s and Hamilton’s equations

where Q



is the ith generalized applied force which is not derived from the potential energy

portion of the Hamiltonian function.

Now let us assume that very large forces are applied to the system over an inﬁnitesimal

time interval t, beginning at time t

. Let us integrate (2.305) over the interval t .We

obtain



+t



∂ H

∂q



dt =



+t



dt (i = 1,...,n) (2.306)

The term ∂ H/∂q

remains ﬁnite during the impulse, so its integral can be neglected. Thus

we obtain

p

(i = 1,...,n) (2.307)

for this unconstrained system. The generalized impulse is



+t



dt (i = 1,...,n) (2.308)

and

p



+t

dt =



j=1



(i = 1,...,n) (2.309)

where we assume that the qs are ﬁxed during the impulse. Thus, the 

qs can be obtained

by solving



j=1



(i = 1,...,n) (2.310)

as we found earlier in (1.360).

Now consider an unconstrained system of N particles whose positions are given by

the Cartesian coordinates x

,...x

. Suppose that corresponding impulses

,...,

are applied to the system during the inﬁnitesimal interval t. The generalized impulse

associated with q



k=1

∂x

∂q



j=1

· γ

(2.311)

in agreement with (1.359).

Lagrangian approach

Let us begin with the fundamental form of Lagrange’s equation, namely,



∂T

∂



−

∂T

∂q

= Q

(i = 1,...,n) (2.312)