Greenwood D.T. Advanced Dynamics

Подождите немного. Документ загружается.

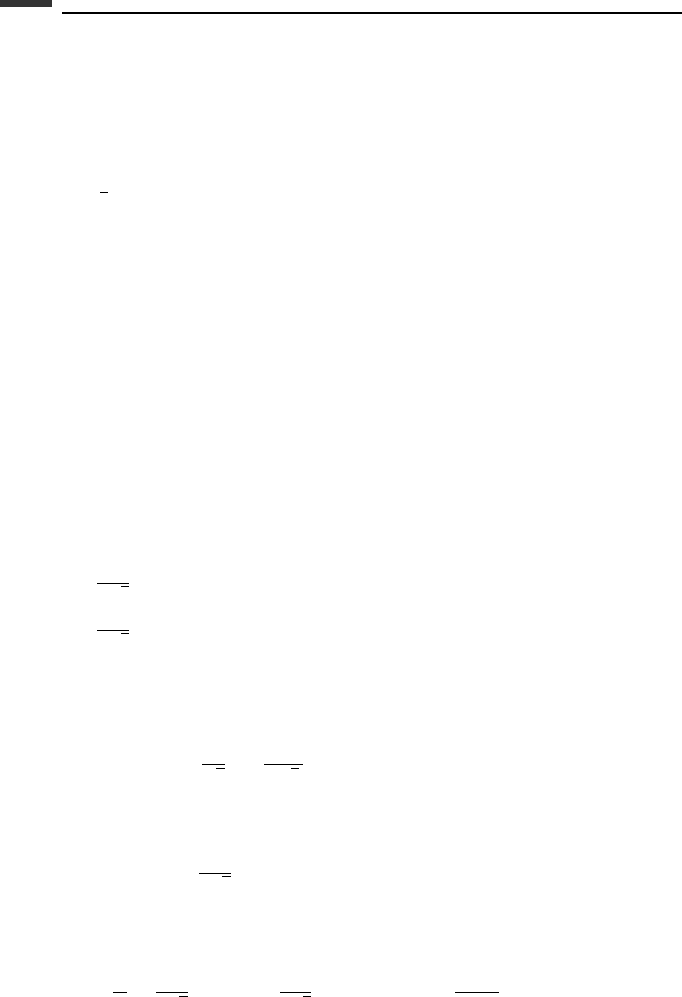
129 Impulse response, analytical methods

Let us use the basic equation (2.365), namely,



i=1



j=1

(

−

)δw

= 0 (2.381)

and thereby avoid having to evaluate Lagrange multipliers. The kinetic energy at t = 0

T =

) (2.382)

which leads to

= m

= m, m

= m

= 0 (2.383)

In accordance with (2.366) the virtual velocities must satisfy

δw

+ δw

= 0 (2.384)

Let us take δw

= 1 and δw

=−1. Then (2.381) results in

[

(

r − v

) −(

y + v

)

]

= 0

r −

y − 2v

= 0 (2.385)

Upon solving (2.380) and (2.385) we obtain

r =

lω

√

+ v

(2.386)

y =

lω

√

− v

(2.387)

These

qs apply at t = 0

The impulse

is obtained by using the principle of impulse and momentum in the

vertical direction.

= m



y + v

lω

√



3mlω

√

(2.388)

Similarly, from the principle of impulse and momentum in the horizontal direction, we

obtain

= m(

r − v

) =

mlω

√

(2.389)

Now let us consider the kinetic energy of this system with a suddenly moving constraint.

The increase in kinetic energy is

T =





lω

√

+ v





lω

√

− v





− mv

(2.390)

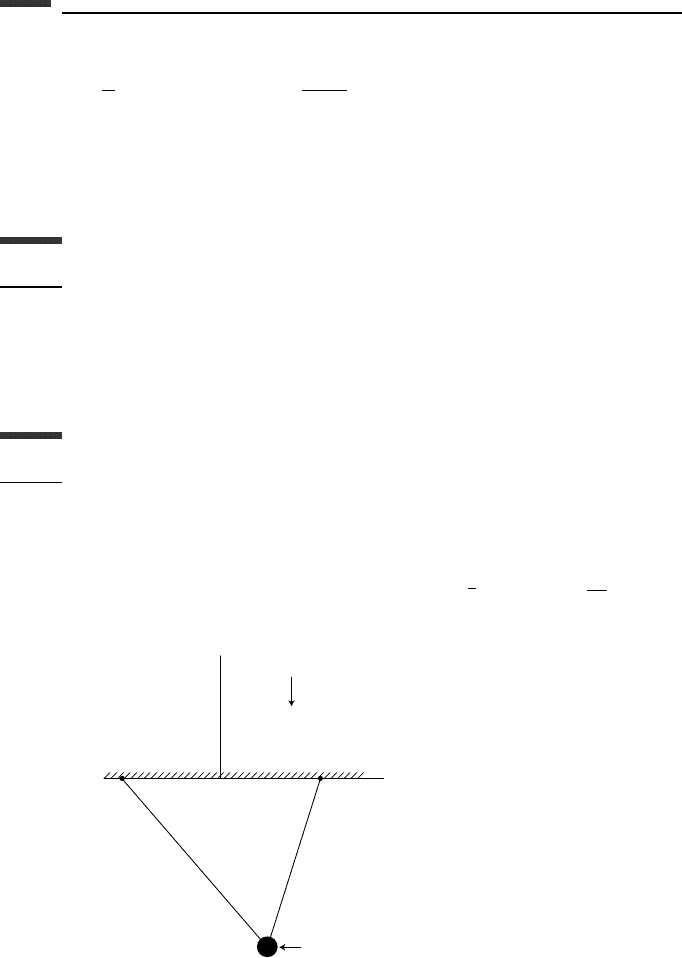
130 Lagrange’s and Hamilton’s equations

From (2.369) the kinetic energy of relative motion is

K =

[(

r − v

)

+ (

y + v

)

] =

(2.391)

We see that

T = K (2.392)

for this system with an acatastatic constraint given by (2.380).

2.7 Bibliography

Desloge, E. A. Classical Mechanics, Vol. 1. New York: John Wiley and Sons, 1982.

Ginsberg, J. H. Advanced Engineering Dynamics, 2nd edn. Cambridge, UK: Cambridge University

Press, 1995.

Greenwood, D. T. Principles of Dynamics, 2nd edn. Englewood Cliffs, NJ: Prentice-Hall, 1988.

Pars, L. A. A Treatise on Analytical Dynamics. London: William Heinemann, 1965.

2.8 Problems

2.1. A string of length 2L is attached at the ﬁxed points A and B which are separated by

a horizontal distance L. A particle of mass m can slide without friction on the string

which remains taut, resulting in an elliptical path. (a) Using Lagrange’s equation

and (x , y) as the particle coordinates, ﬁnd the differential equations of motion. (b)

Assume the initial conditions x(0) = 0, y(0) =−(

√

3/2)L,

x(0) =

√

gL,

y(0) = 0.

Solve for x

max

during the motion and the initial string tension P.

(x, y)

Figure P 2.1.

131 Problems

2.2. Consider the dumbbell system of Example 2.3 on page 83. Suppose there is a Coulomb

friction coefﬁcient µ for skidding, that is, sliding in a direction perpendicular to the

knife edge, but there is no friction for sliding along the knife edge. (a) What are

the differential equations of motion, assuming that skidding occurs? (b) Write an

inequality of the form |f (q,

q)| > C which is the necessary and sufﬁcient condition

for skidding to occur.

2.3. A particle of mass m can slide on a smooth rigid wire in the form of the parabola

y = x

under the action of gravity. (a) Obtain the x and y differential equations of

motion and solve for

x as a function of (x,

x). (b) Assuming the initial conditions

x(0) = x

x(0) = 0, solve for

x(x ).

Figure P 2.3.

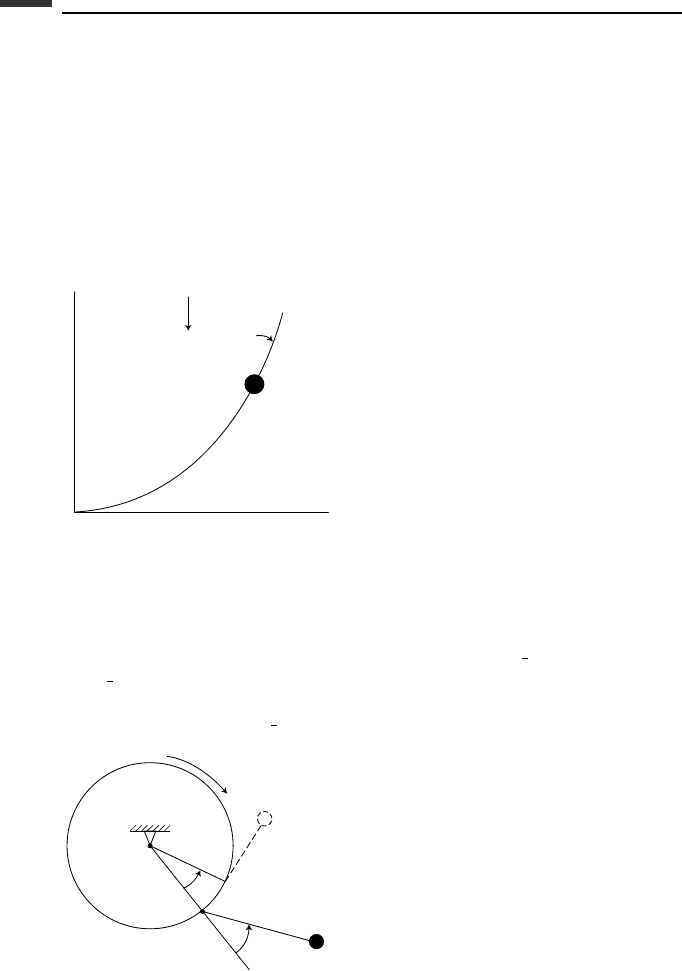
2.4. A cylinder of radius r rotates at a constant rate ω about its ﬁxed central axis. A particle

of mass m is attached to point P on its circumference by a ﬂexible rope of length L.

(a) Assume that the initial value φ(0) = 0 and the absolute velocity of the particle is

zero at this time. Solve for

φ as a function of φ for 0 ≤ φ ≤

π. (b) After φ reaches

π the rope begins to wrap around the cylinder and its straight portion is of length

l = L − r θ . Assuming that the initial value of

θ for this phase of the motion is equal

to the value of

φ at φ =

π,solvefor

θ as a function of l and show that

θ = r

Figure P 2.4.

132 Lagrange’s and Hamilton’s equations

2.5. A particle P of mass m is attached by a ﬂexible massless string of constant length L

to a point A on the rim of a smooth ﬁxed vertical cylinder of radius R. The string can

wrap around the cylinder, but leaves at point C, creating a straight portion CP.At

any given time, all portions of the string maintain the same slope angle φ relative to

a horizontal plane. (a) Using (θ,φ) as generalized coordinates, obtain the differential

equations of motion. (b) Solve for the tension in the string. Assume that the string

remains taut and the distance CP > 0.

Figure P 2.5.

2.6. A particle of mass m moves on the surface of a spherical earth of radius R which

rotates at a constant rate . Linear damping with a damping coefﬁcient c exists for

motion of the particle relative to the earth’s surface. Choose an inertial frame at the

center of the earth and use (θ,φ) as generalized coordinates, where θ is the latitude

angle (positive north of the equator) and φ is the longitude angle (positive toward the

east). (a) Obtain the differential equations of motion. (b) Show that the work rate

of the damper acting on the particle plus its work rate

acting on the earth plus the

energy dissipation rate

D sums to zero.

2.7. A dumbbell consists of two particles, each of mass m, connected by a massless rod of

length l. A knife edge is located at particle 1 and is aligned at 45

◦

to the longitudinal

direction, as shown in Fig. P 2.7. Using (x, y,φ) as generalized coordinates, ﬁnd the

differential equations of motion of the system.

2.8. Two particles, each of mass m, can slide on the horizontal xy-plane (Fig. 2.8).

Particle 1 at (x, y) has a knife-edge constraint and is attached to a massless rigid

rod. Particle 2 can slide without friction on this rod and is connected to particle 1

by a spring of stiffness k and unstressed length l

. Using (x , y,φ,s) as generalized

coordinates, obtain the differential equations of motion.

133 Problems

(x, y)

+ s

Figure P 2.7. Figure P 2.8.

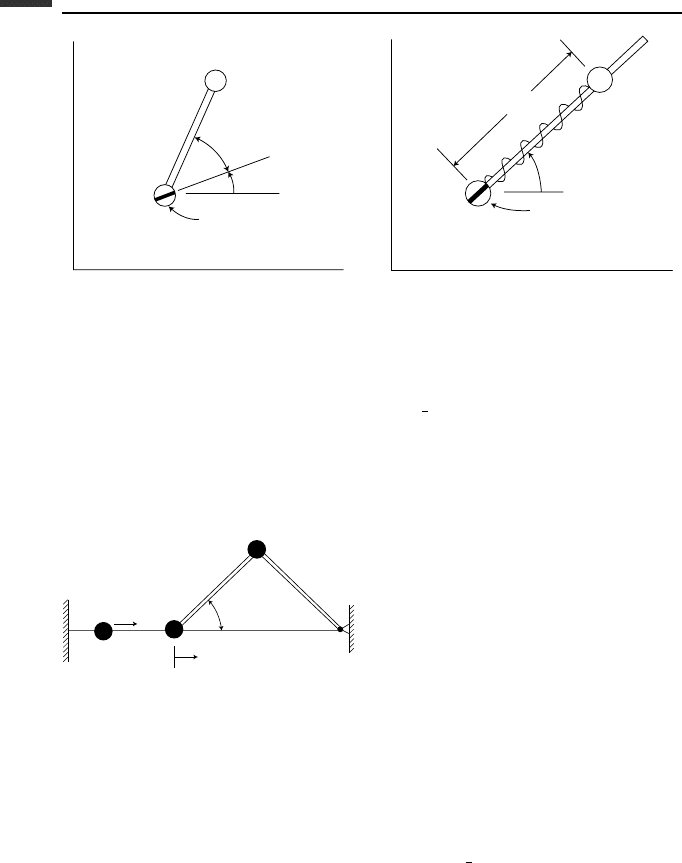
2.9. Particles B and C, each of mass m, are motionless in the position shown in Fig. P 2.9

when particle B is hit by particle A, also of mass m and moving with speed v

. The

coefﬁcient of restitution for this impact is e =

. Particles A and B can move without

friction on a ﬁxed rigid wire, the displacement of B being x. There is a joint at C

and the two rods of length l are each massless. (a) Find the velocity

x of particle B

immediately after impact. (b) What is the impulse

P transmitted by rod BC?

45°

e = −

Figure P 2.9.

2.10. Three particles, each of mass m, are connected by strings of length l to form an equi-

lateral triangle (Fig. P 2.10). The system is rotating in planar motion about its ﬁxed

center of mass at an angular rate

φ = ω

when string BC suddenly breaks. (a) Take

(φ,θ) as generalized coordinates and use the Routhian procedure to obtain the differ-

ential equation for θ in the motion which follows. (b) Solve for the value of

θ when the

system ﬁrst reaches a straight conﬁguration with θ =

π, assuming the strings remain

taut.

2.11. A rigid wire in the form of a circle of radius r rotates about a ﬁxed vertical diameter

at a constant rate  (Fig. P 2.11). A particle of mass m can slide on the wire,

and there is a coefﬁcient of friction µ between the particle and the wire. Find the

differential equation for the position angle θ .

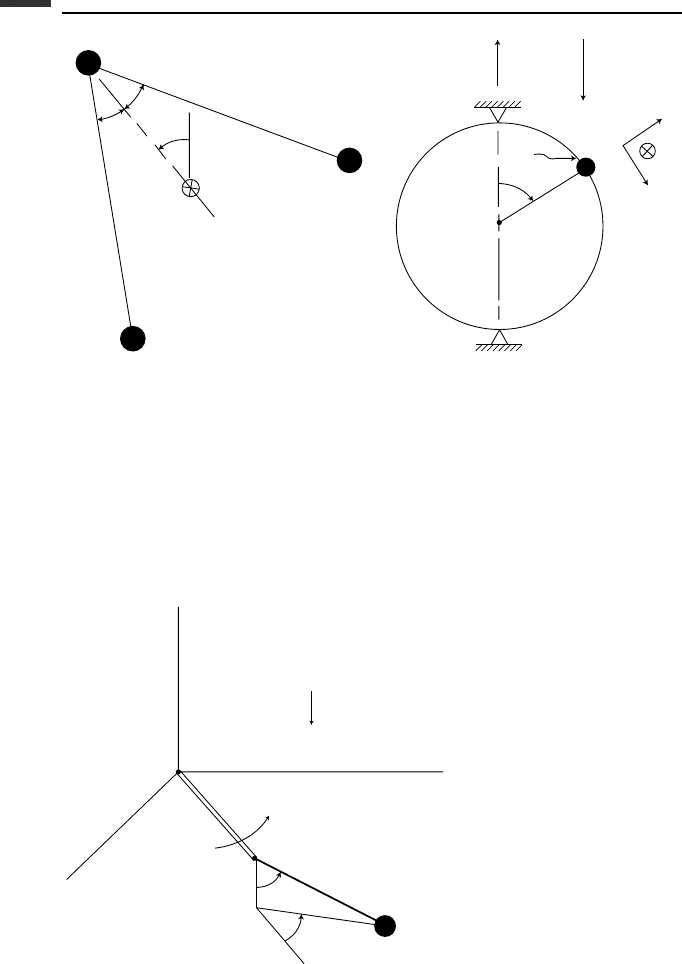
134 Lagrange’s and Hamilton’s equations

c.m.

Ω

Figure P 2.10. Figure P 2.11.

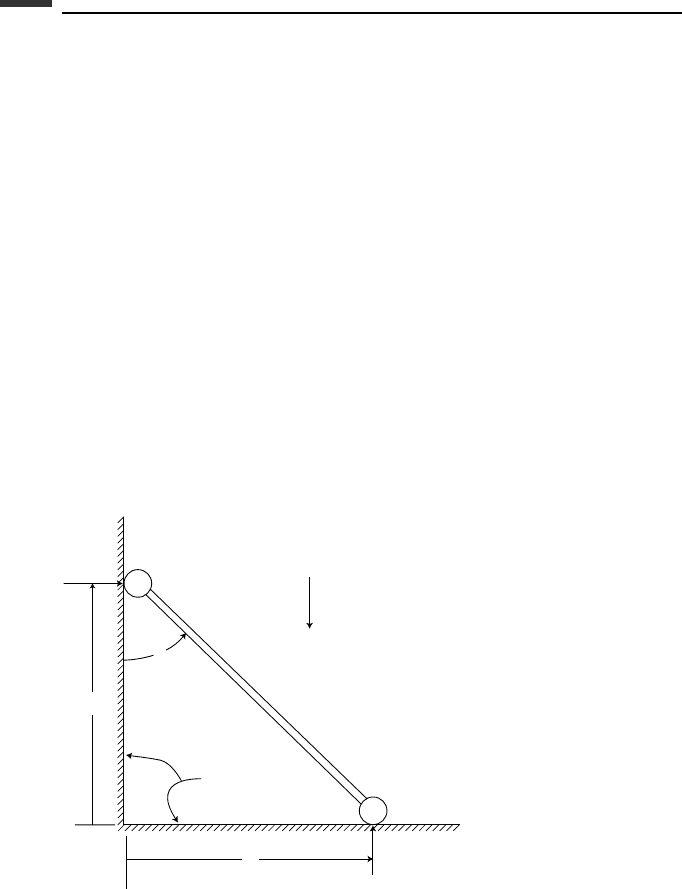
2.12. A rod of length R rotates in the horizontal xy-plane at a constant rate ω. A pendulum

of mass m and length l is attached to point P at the end of the rod. The orientation of

the pendulum relative to the rod is given by the angle θ measured from the downward

vertical and the angle φ between the vertical plane through the pendulum and the

direction OP. (a) Using (θ,φ) as generalized coordinates, obtain the differential

equations of motion. (b) Write the expression for the energy integral of this

system.

Figure P 2.12.

135 Problems

2.13. An xy Cartesian frame rotates at a constant angular rate  about the origin in planar

motion. The position of a particle of mass m is (x, y) relative to the rotating frame.

There is an impulsive constraint, discontinuous at time t

, which is given by

y = 0

(t < t

y = v

(t > t

). The position at t = t

is (x

, y

) and

x(t

−

) =

. (a) Solve

for the values of the relative velocity components (

y) at time t

. (b) Find T

as well as the increase T in the total kinetic energy. (c) Solve for the constraint

impulse.

2.14. A particle of mass m can move without friction on a horizontal spiral of the form

r = kθ, as in Fig. 1.8 on page 13. (a) Choose (r,θ) as generalized coordinates and

write the differential equations of motion using Lagrange’s equation. (b) Assuming

that the particle starts at the origin with speed v

,solvefor

r and the normal

constraint force N as functions of r . (c) Now add Coulomb friction with coefﬁcient

µ and obtain a single equation of motion giving

r as a function of r and

2.15. A dumbbell AB can move in the vertical xy-plane. There is a coefﬁcient of friction

µ for sliding at A and B. The normal constraint forces are N

and N

,asshown.(a)

Assuming downward sliding (

x > 0), write the differential equations of motion in

the forms

x =

x(x , y,

y) and

y =

y(x, y,

y), that is, eliminate λ, N

, and N

by expressing them in terms of these variables. (b) Use θ as a single generalized

coordinate and write the differential equation for θ in the form

θ =

θ(θ,

θ).

Figure P 2.15.

2.16. Four particles, each of mass m, are connected by massless rods of length l,asshown

in Fig. P 2.16. There is a joint at each particle. Assume planar motion with no

136 Lagrange’s and Hamilton’s equations

external forces, so the center of mass can be considered ﬁxed in an inertial frame.

(a) Using (r

, r

,θ) as generalized coordinates, obtain the differential equations of

motion. Reduce these equations to three equations of motion, each involving a single

variable and its time derivatives. (b) Assuming an initially square conﬁguration with

(0) = v

(0) =−v

, θ(0) = 0,

θ(0) = ω

,solveforr

, r

, and θ as functions of

time.

c.m.

Figure P 2.16.

2.17. The polar coordinates (r,θ) deﬁne the position of a particle of mass m which is initially

constrained to move at a constant angular rate

θ = ω

along a frictionless circular path

of radius R. Then, at time t = 0, the radius of the circular constraint starts increasing

at a constant rate

r = v

. When t = R/v

the expansion of the constraint suddenly

stops, and r = 2R for t > R/v

. (a) Solve for the constraint impulses at times t = 0

and t = R/v

. (b) What is the ﬁnal velocity of the particle? (c) Find the work done

on the particle by each of the constraint impulses and by the nonimpulsive constraint

force.

2.18. Particles A and B can slide without friction on the vertical y-axis (Fig. P 2.18). Particle

C can slide without friction on the horizontal x-axis. Particles B and C are connected

by a massless rod of length l while particles A and C are connected by a massless rod

of length

√

3l. There are joints at the ends of the rods. (a) Use (θ

,θ

) as generalized

coordinates and write the holonomic constraint equation. (b) Obtain expressions

for the kinetic and potential energies in terms of θ

and

; that is, eliminate θ

and

by using the constraint equation. (c) Assume the initial conditions θ

(0) = 30

◦

(0) = 0, θ

(0) = 60

◦

(0) = 0. Solve for the velocity of particle B when it

ﬁrst passes through the origin. (d) Solve for the acceleration of particle A at this

time.

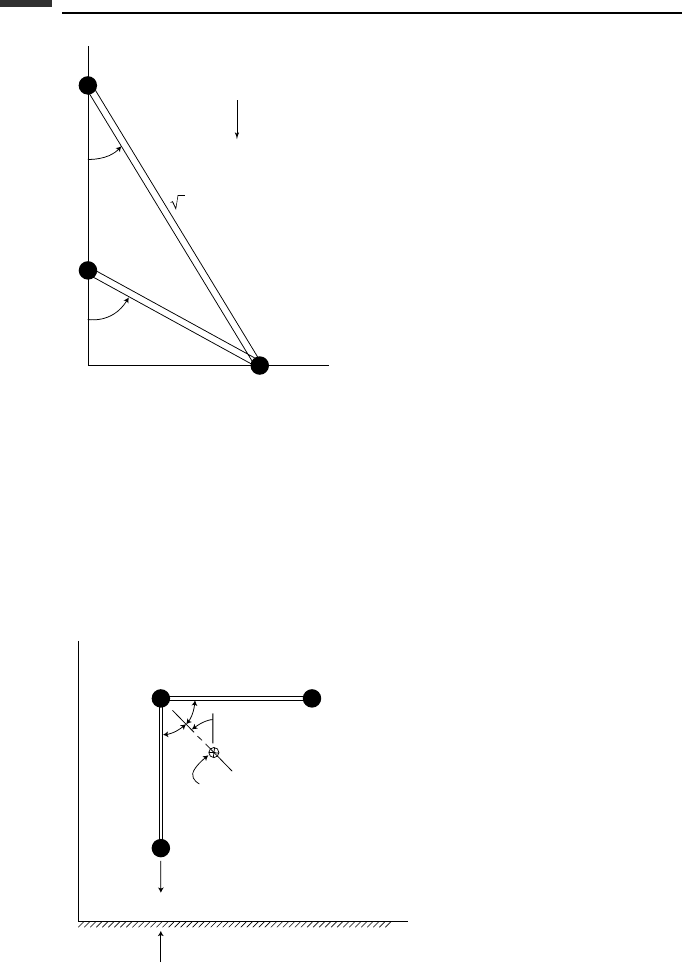
137 Problems

3 l

Figure P 2.18.

2.19. Three particles, each of mass m, are connected by massless rods AB and AC with

a joint at A. The system is translating in the negative y direction with speed v

when particle C hits a ﬁxed smooth wall and there is a coefﬁcient of restitution

e = 1. Use the generalized coordinates (θ,φ,x, y). Assume that the conditions just

before impact are θ(0

−

) = 45

◦

θ(0

−

) = 0,φ(0

−

) = 45

◦

φ(0

−

) = 0,

x(0

−

) = 0,

y(0

−

) =−v

. Find: (a) the constraint impulse

N during impact and the initial

conditions just after impact; (b) the θ and φ equations of motion; (c) the minimum

value of θ and the value of

φ at this time.

c.m.

(x, y)

Figure P 2.19.

138 Lagrange’s and Hamilton’s equations

2.20. Four particles, each of mass m, can move on the horizontal xy-plane without friction.

They are connected by four massless rods of length l with joints at the particles.

(a) Using (x , y,θ,φ) as generalized coordinates, obtain the differential equations

of motion. (b) Assuming the initial conditions x(0) = y(0) = 0,

x(0) =

y(0) =

0,θ(0) = φ(0) = 0,

θ(0) =

> 0,

φ(0) =

> 0, solve for the tensile forces in

the rods. (c) Assuming that any particle collisions are purely elastic, ﬁnd the period

of the motion in φ.

c.m.

(x, y)

Figure P 2.20.

2.21. Two particles, each of mass m, are connected by a rigid massless rod of length l

(Fig. P2.21). Particle 1 slides without friction on the horizontal xy-plane. Because of

the conservation of horizontal momentum, an inertial frame can be found such that the

motion of the center of mass is strictly vertical. (a) Using (θ,φ) as generalized coordi-

nates, obtain the differential equations of motion. (b) Assuming the initial conditions

θ(0) = π/4,

θ(0) = 0,φ(0) = 0,

φ(0) =

, solve for the value of

θ at the instant

just before θ reaches zero. Assume that particle 1 remains in contact with the xy-plane.

such that particle 1 will leave the xy-plane at

t = 0.