Greenwood D.T. Advanced Dynamics
Подождите немного. Документ загружается.


149 Kinematical preliminaries
The antisymmetric part of the rotation matrix is
C
a
= sin φ
0 a
z
−a
y
−a
z
0 a
x
a
y
−a
x
0
(3.36)
Let us introduce the tilde matrix notation
˜
a ≡
0 −a
z
a
y
a
z
0 −a
x
−a
y
a
x
0
(3.37)
Then
C
a
=−sin φ
˜
a (3.38)
and the complete rotation matrix is
C = C
s
+ C
a
= cos φ U + (1 − cos φ)aa
T
− sin φ
˜
a (3.39)
In detail, we find that
c
xx
= (1 − cos φ)a
2
x
+ cos φ = a
2
x
+
a
2
y
+ a
2
z
cos φ
c
yy
= (1 − cos φ)a
2
y
+ cos φ = a
2
y
+
a
2
z
+ a
2
x
cos φ
c
zz
= (1 − cos φ)a
2
z
+ cos φ = a
2
z
+
a
2
x
+ a
2
y
cos φ
c
xy
= (1 − cos φ)a
x
a
y
+ a
z
sin φ
c
yx
= (1 − cos φ)a
y
a
x
− a
z
sin φ (3.40)
c
xz
= (1 − cos φ)a
x
a
z
− a
y
sin φ
c
zx
= (1 − cos φ)a
z
a
x
+ a
y
sin φ
c
yz
= (1 − cos φ)a
y
a
z
+ a
x
sin φ
c
zy
= (1 − cos φ)a
z
a
y
− a
x
sin φ
Euler parameters
Another method of specifying the orientation of a rigid body is by the use of four Euler
parameters. The Euler parameters are based on the mathematics of quaternions and are
closely related to axis and angle variables. We shall define the Euler parameters in terms of
axis and angle variables as follows:
x
= a
x
sin
φ
2
y
= a
y
sin
φ
2
(3.41)
z
= a
z
sin
φ
2
η = cos
φ
2
150 Kinematics and dynamics of a rigid body
where we recall that 0 ≤ φ ≤ π. These four parameters are constrained by the single equa-
tion
2
x
+
2
y
+
2
z
+ η
2
= 1 (3.42)
Euler parameters have the advantages of having no singular orientations and only one
equation of constraint. Thus, they exhibit a good balance between overall accuracy and
computational efficiency.
Let us define the Euler 3-vector as
=
x
i +
y
j +
z
k = a sin
φ
2
(3.43)
whose magnitude is
=
2
x
+
2
y
+
2
z
1
2
(3.44)
Then
2
+ η
2
= 1 (3.45)
To convert from the direction cosines of the rotation matrix to Euler parameters, we can
use
x
=
1
4η
(c
yz
− c
zy
)
y
=
1
4η
(c
zx
− c
xz
)
(3.46)
z
=
1
4η
(c
xy
− c
yx
)
η =
1
2
√
1 +tr C, 0 ≤ φ ≤ π
Conversely, to convert from Euler parameters to the rotation matrix, we obtain
C =
1 −2
2
y
+
2
z
2(
x
y
+
z
η)2(
x
z
−
y
η)
2(
y
x
−
z
η)1− 2(
2
z
+
2
x
)2(
y
z
+
x
η)
2(
z
x
+
y
η)2(
z
y
−
x
η)1− 2
2
x
+
2
y
(3.47)
Another form of this result is the matrix equation
C = (1 −2
T
)U + 2
T
− 2η ˜ (3.48)
where
T
=
2
x
+
2
y
+
2
z
and we see that
1 −2
T
= η
2
−
2
x
+
2
y
+
2
z
= cos
2
φ
2
− sin
2
φ
2
= cos φ (3.49)

151 Kinematical preliminaries
Successive rotations
In the earlier discussion of rotation matrices, we found that successive rotations of a co-
ordinate frame are accomplished by successive premultiplications by the corresponding
rotation matrices. The question arises whether a similar procedure is available for use with
Euler parameters. The answer is that such a procedure is indeed available, and consists in
premultiplying the current Euler 4-vector by the matrix
R =
η
z
−
y
x
−
z
η
x
y
y
−
x
η
z
−
x
−
y
−
z
η
(3.50)
where the components of are taken in the body-fixed frame.
As an example, suppose a first rotation “a”, represented by (
xa
,
ya
,
za
,η
a
), is followed
by a second rotation “b” given by (
xb
,
yb
,
zb
,η
b
). These two rotations are equivalent to
a single rotation given by
x
y
z
η
=
η
b
zb
−
yb
xb
−
zb
η
b
xb
yb
yb
−
xb
η
b
zb
−
xb
−
yb
−
zb
η
b
xa
ya
za
η
a
(3.51)
An alternate form involving the vector and the scalar η is given by the two equations
= η
b
a
+ η
a
b
+
a
×
b
(3.52)
η = η
a
η
b
−
a
·
b
(3.53)
where the vectors are again expressed relative to the body-fixed frame. Notice that the
overall axis of rotation depends on the order of the individual rotations, but the angle of
rotation does not.
In terms of axis and angle variables, the sequence of two rotations is equivalent to a single
rotation φ about an axis a where
cos
φ
2
= cos
φ
a
2
cos
φ
b
2
− sin
φ
a
2
sin
φ
b
2
a
a
· a
b
(3.54)
and, using this value of φ,
a =
1
sin
φ
2
sin
φ
a
2
cos
φ
b
2
a
a
+ cos
φ
a
2
sin
φ
b
2
a
b
+ sin
φ
a
2
sin
φ
b
2
a
a
× a
b
(3.55)
in agreement with (3.52) and (3.53). Again, for a sequence of two given rotations about
specified axes, the final equivalent angle φ is independent of the order of rotation, but the
final axis of rotation is not.

152 Kinematics and dynamics of a rigid body
Angular velocity
Consider the rotation matrix which gives the orientation of a body-fixed xyz frame relative
to an inertial XYZ frame. Let (i, j, k) be the unit vectors for the xyz frame and let (I, J, K)
be the corresponding unit vectors for the inertial frame. Then we can write
C =
i · Ii· Ji· K
j · Ij· Jj· K
k · Ik· Jk· K
(3.56)
that is, c
xx
= i · I, c
xy
= i · J, and so on in accordance with the direction cosine definitions.
Now suppose that the xyz frame has an angular velocity
ω = ω
x
i + ω
y
j + ω
z
k (3.57)
This will result in changing values of the elements of the rotation matrix. For example,
˙
c
xx
=
di
dt
· I = (ω × i) · I
= (ω
z
j − ω
y
k) ·I = c
yx
ω
z
− c
zx
ω
y
(3.58)
A similar procedure results in the complete set of Poisson equations.
˙
c
xx
= c
yx
ω
z
− c
zx
ω
y
˙
c
xy
= c
yy
ω
z
− c
zy
ω
y
˙
c
xz
= c
yz
ω
z
− c
zz
ω
y
˙
c
yx
= c
zx
ω
x
− c
xx
ω
z
˙
c
yy
= c
zy
ω
x
− c
xy
ω
z
(3.59)
˙
c
yz
= c
zz
ω
x
− c
xz
ω
z
˙
c
zx
= c
xx
ω
y
− c
yx
ω
x
˙
c
zy
= c
xy
ω
y
− c
yy
ω
x
˙
c
zz
= c
xz
ω
y
− c
yz
ω
x
These equations can be written in the matrix form
˙
C =−˜ωC (3.60)
where
˜ω =
0 −ω
z
ω
y
ω
z
0 −ω
x
−ω
y
ω
x
0
(3.61)
Upon solving (3.60) for ˜ω, we obtain
˜ω =−
˙
CC
T
= C
˙
C
T
(3.62)

153 Kinematical preliminaries
which results in
ω
x
= c
zx
˙
c
yx
+ c
zy
˙
c
yy
+ c
zz
˙
c
yz
ω
y
= c
xx
˙
c
zx
+ c
xy
˙
c
zy
+ c
xz
˙
c
zz
(3.63)
ω
z
= c
yx
˙
c
xx
+ c
yy
˙
c
xy
+ c
yz
˙
c
xz
Now consider the angular velocity of a rigid body in terms of axis and angle variables. It
can be shown that
ω =
˙
φa + sin φ
˙
a + (1 −cos φ) a×
˙
a (3.64)
where the three terms represent mutually orthogonal components.
We can solve for
˙
φ and
˙
a in terms of ω by first taking the dot product of a with (3.64),
obtaining
˙
φ = a · ω (3.65)
Next, noting that a × (a ×
˙
a) =−
˙
a, we obtain from (3.64) that
a × ω = sin φ a×
˙
a − (1 −cos φ)
˙
a (3.66)
and
a × (a × ω) =−sin φ
˙
a − (1 −cos φ) a×
˙
a (3.67)
Recall that
cot
φ
2
=
sin φ
1 −cos φ
=
1 +cos φ
sin φ
(3.68)
so
cot
φ
2
a × (a × ω) =−(1 + cos φ)
˙
a − sin φ a×
˙
a (3.69)
Then
a × ω + cot
φ
2
a×(a × ω) =−2
˙
a (3.70)
or
˙
a =−
1
2
a × ω + cot
φ
2
a×(a × ω)
(3.71)
It is convenient for computational reasons to find the component rates (
˙
a
x
,
˙
a
y
,
˙
a
z
)ofa
relative to the rotating body axes. Using vector notation, we have
(
˙
a)
r
=
˙
a − ω × a =
1
2
a × ω − cot
φ
2
a × (a × ω)
(3.72)
where
(
˙
a)
r
=
˙
a
x
i +
˙
a
y
j +
˙
a
z
k (3.73)
154 Kinematics and dynamics of a rigid body
Similar equations in terms of Euler parameters can be obtained by first recalling
that
= a sin
φ
2
,η= cos
φ
2
(3.74)
and
˙η =−
1
2
˙
φ sin
φ
2
(3.75)
Then
˙η =−
1
2
a · ω sin
φ
2
=−
1
2
· ω (3.76)
A differentiation of (3.74) with respect to time and the use of (3.65) results in
˙ =
1
2
cos
φ
2
(a · ω)a + sin
φ
2
˙
a (3.77)
Now substitute for
˙
a from (3.71) and note that a × (a × ω) = (a · ω)a − ω. We obtain
˙ =
1
2
cos
φ
2
(a · ω)a −
1
2
sin
φ
2
a × ω + cot
φ
2
(
(a · ω)a − ω
)
=−
1
2
sin
φ
2
a × ω +
1
2
cos
φ
2
ω
=−
1
2
× ω +
1
2
ηω (3.78)
The basic Euler parameter rates are given by (3.76) and (3.78). However, for computa-
tional purposes we need to find ( ˙)
r
, that is, the values of ˙
x
,˙
y
, and ˙
z
. We obtain
(˙)
r
= ˙ + × ω =
1
2
× ω +
1
2
ηω (3.79)
or, in detail,
˙
x
=
1
2
(ω
z
y
− ω
y
z
+ ω
x
η)
˙
y
=
1
2
(ω
x
z
− ω
z
x
+ ω
y
η)
(3.80)
˙
z
=
1
2
(ω
y
x
− ω
x
y
+ ω
z
η)
˙η =−
1
2
(ω
x
x
+ ω
y
y
+ ω
z
z
)
These kinematic differential equations are widely used and, upon numerical integration,
yield the orientation of a rigid body as a function of time. Note that, in contrast to the
comparable (
˙
a)
r
equations, they do not involve trigonometric functions. They require the
body-axis components of ω as inputs, and these are often obtained from the solution of the
dynamical equations.

155 Kinematical preliminaries
Conversely, the body-axis components of the angular velocity ω can be obtained from
(3.80) and the Euler parameter constraint equation (3.42). They are
ω
x
= 2(η ˙
x
+
z
˙
y
−
y
˙
z
−
x
˙η)
ω
y
= 2(η ˙
y
+
x
˙
z
−
z
˙
x
−
y
˙η) (3.81)
ω
z
= 2(η ˙
z
+
y
˙
x
−
x
˙
y
−
z
˙η)
Infinitesimal rotations
Consider a body-fixed xyz frame and an inertial XYZ frame which initially coincide. Then
let the xyz frame undergo a sequence of three infinitesimal rotations; namely, θ
x
about the
x-axis, θ
y
about the y-axis, and θ
z
about the z-axis. The overall rotation matrix is equal to
the product of the three individual rotation matrices. If we retain terms to first order in the
small θs, we obtain
C =
1 θ
z
0
−θ
z
10
001
10−θ
y
01 0
θ
y
01
10 0
01θ
x
0 −θ
x
1
=
1 θ
z
−θ
y
−θ
z
1 θ
x
θ
y
−θ
x
1
(3.82)
or
C = U −
˜
θ (3.83)
where
˜
θ =
0 −θ
z
θ
y
θ
z
0 −θ
x
−θ
y
θ
x
0
(3.84)
and U is a 3 × 3 unit matrix.
It is important to realize that the order of the infinitesimal rotations does not matter,
in contrast to the situation for finite rotations, where the order must be specified. We can
express a general infinitesimal rotation as a vector
θ = θ
x
I + θ
y
J + θ
z
K (3.85)
where I, J, K are inertial unit vectors. To first order in terms of body-fixed unit vectors,
θ = θ
x
i + θ
y
j + θ
z
k (3.86)
The component infinitesimal rotations θ
x
, θ
y
, θ
z
can be taken in any order. Hence, a sequence
of several infinitesimal rotations is equivalent to a single rotation equal to their vector sum.

156 Kinematics and dynamics of a rigid body
The angular velocity of the rigid body is equal to an infinitesimal rotation θ divided by
the corresponding time interval t, in the limit as θ and t approach zero. Thus, to first
order,
ω = lim
t→0
θ
t
=
˙
θ =
˙
θ
x
i +
˙
θ
y
j +
˙
θ
z
k (3.87)
where ω is finite, in general. We see that
ω
x
=
˙
θ
x
,ω
y
=
˙
θ
y
,ω
z
=
˙
θ
z
(3.88)
Upon differentiation of (3.83), we obtain
˙
C =−
˜
˙
θ =−˜ω (3.89)
for infinitesimal rotations.
If we use axis and angle variables, we find that
θ = φa (3.90)
where
φ =
θ
2
x
+ θ
2
y
+ θ
2
z
(3.91)
Thus,
a
x
=
θ
x
φ
, a
y
=
θ
y
φ
, a
z
=
θ
z
φ
(3.92)
The angular velocity of the rigid body is
ω =
˙
θ =
˙
φa + φ
˙
a =
˙
φa (3.93)
where we note that φ
˙
a is infinitesimal.
In terms of Euler parameters, we have, from (3.43) and (3.90) for small φ,
=
1
2
θ (3.94)
or
x
=
1
2
θ
x
,
y
=
1
2
θ
y
,
z
=
1
2
θ
z
,η= 1 (3.95)
The angular velocity is
ω =
˙
θ = 2˙ (3.96)
where
˙ = ˙
x
i + ˙
y
j + ˙
z
k (3.97)

157 Kinematical preliminaries
Instantaneous axis of rotation
Euler’s theorem states that the most general displacement of a rigid body with a fixed base
point is equivalent to a single rotation about some axis through that point. A completely
general displacement of a rigid body, however, would require a displacement of all points in
the body. So, if one is given a base point fixed in the body, then the most general displacement
is equivalent to (1) a translation of the body resulting in the correct final position of the
base point, followed by (2) a rotation about an axis through the final position of the base
point which gives the correct final orientation. Now, for a given base point, it is apparent
that the translation and rotation are independent and can take place in any order or possibly
together. Furthermore, for any nonzero rotation angle φ and a given axis orientation, it is
always possible to choose a location of the axis of rotation such that any given base point
in the body will undergo a prescribed translation in a plane perpendicular to the axis of
rotation. Hence, all that remains is to give the base point the required translation parallel
to the axis of rotation. Thus we obtain Chasles’ Theorem: The most general displacement
of a rigid body is equivalent to a screw displacement consisting of a rotation about a fixed
axis plus a translation parallel to that axis.
Now suppose that a rigid body undergoes a general infinitesimal displacement during
the time interval t. Then, in accordance with Chasles’ theorem, the motion in the limit as
t approaches zero can be considered as the superposition of an angular velocity ω about
some axis plus a translational velocity v in a direction parallel to ω. All points in the body
that lie on this axis have the same velocity v along the axis. This axis exists for all cases in
which ω = 0 and is known as the instantaneous axis of rotation.
For the special case of planar motion, the velocity v is equal to zero; and the in-
stantaneous axis becomes the instantaneous center of rotation. The instantaneous axis
of rotation, or the instantaneous center for planar motion, can move relative to the
body and relative to inertial space. However, at the instant under consideration these
points in the rigid body have no velocity component normal to the instantaneous axis of
rotation.
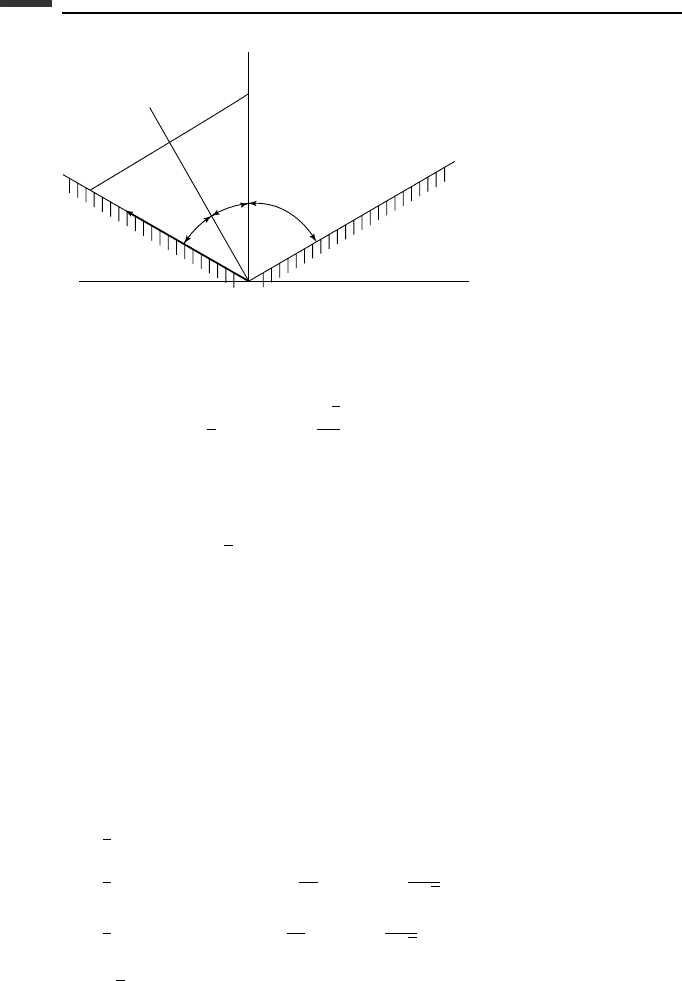
Example 3.1 A solid cone of semivertex angle 30
◦
rolls without slipping on the inside
surface of a conical cavity with a semivertex angle at O equal to 60
◦
(Fig. 3.4). The cone
has an angular velocity ω with a constant magnitude ω
0
. We wish to determine the values
of the Euler angles, axis and angle variables, Euler parameters, and their rates of change
when the configuration is as shown in the figure.
Let us use Type II Euler angles. The three successive rotations about the Z, x, and z
axes, respectively, are φ = 0, θ = 30
◦
, and ψ = 0. From (3.24), or directly by observation
of Fig. 3.4, we find that the rotation matrix is
C =
10 0
0
√
3
2
1
2
0 −
1
2
√
3
2
(3.98)
158 Kinematics and dynamics of a rigid body
Z
y
O
Y
z
cone
30˚
30˚
60˚
w
Figure 3.4.
The cone rotates about its line of contact. Therefore, the body-axis components of its
angular velocity ω are
ω
x
= 0,ω
y
=−
1
2
ω
0
,ω
z
=
√
3
2
ω
0
(3.99)
Then, using (3.19), the Euler angle rates are
˙
φ = csc θ (ω
x
sin ψ + ω
y
cos ψ) =−ω
0
˙
θ = ω
x
cos ψ − ω
y
sin ψ = 0 (3.100)
˙
ψ = ω
z
−
˙
φ cos θ =
√
3 ω
0
Next, consider axis and angle variables, where φ is now the rotation angle about the
rotation axis a. Since the first and third Euler angle rotations were equal to zero, we see that
the required rotation is 30
◦
about the x -axis. Hence,
a
x
= 1, a
y
= 0, a
z
= 0,φ= 30
◦
(3.101)
This is in agreement with (3.27) and (3.28) which use values from the rotation matrix.
The values of the Euler parameters can now be obtained from (3.41). They are
x
= sin 15
◦
,
y
= 0,
z
= 0,η= cos 15
◦
(3.102)
The corresponding Euler parameter rates are found from (3.80).
˙
x
=
1
2
(ω
z
y
− ω
y
z
+ ω
x
η) = 0
˙
y
=
1
2
(ω
x
z
− ω
z
x
+ ω
y
η) =−
ω
0
2
sin 45
◦
=−
ω
0
2
√
2
(3.103)
˙
z
=
1
2
(ω
y
x
− ω
x
y
+ ω
z
η) =
ω
0
2
cos 45
◦
=
ω
0
2
√
2
˙η =−
1
2
(ω
x
x
+ ω
y
y
+ ω
z
z
) = 0
