Greenwood D.T. Advanced Dynamics

Подождите немного. Документ загружается.

159 Dyadic notation

Now consider the rates of the axis and angle variables. From (3.65) we ﬁnd that

φ = a · ω = 0 (3.104)

Next, recall from (3.71) that

a =−



a × ω + cot

a × (a × ω)



(3.105)

where, for this example,

a × ω =−ω



√

j +



(3.106)

cot

a × (a × ω) =−ω cot

= (2 +

√

3)ω



j −

√



(3.107)

Thus, we obtain

a = ω



−

j +



1 +

√





(3.108)

To ﬁnd the components of

a in the inertial frame, multiply by C

and obtain

a =



1 +

√



(−J + K) (3.109)

The time derivative of a with respect to the rotating body axes is, from (3.72),

(



a × ω − cot

a × (a × ω)





1 +

√



(−j + k) (3.110)

= 0,

=−



1 +

√





1 +

√



(3.111)

Notice that these components are equal to the corresponding components of

a in the inertial

frame. This is explained by the fact that the axis a about which the rotation φ takes place is

ﬁxed in both frames during the rotation, and these frames coincide initially.

3.2 Dyadic notation

Deﬁnition of a dyadic

Dyadics are used in vector equations to represent the second-order tensors that are often

expressed as 3 × 3 matrices. A dyad consists of a pair of vectors such as ab written in a

particular order. A dyadic is the sum of dyads.

160 Kinematics and dynamics of a rigid body

Each vector in 3-space may be expressed in terms of an orthogonal set of unit vectors. If

we choose the same set of unit vectors for a and b, we obtain

a = a

+ a

b = b

+ b

(3.112)

We can deﬁne the dyadic

A = ab =



i=1



j=1

(3.113)

where A

= a

. Thus A consists of the sum of nine terms, each containing a pair of unit

vectors.

Now let us deﬁne the conjugate dyadic by interchanging the vectors in each term. We

obtain



i=1



j=1

(3.114)

A dyadic is symmetric if A = A

;itisskew-symmetric if A =−A

.Anexampleofa

symmetric dyadic is the inertia dyadic.

I = I

ii + I

ij + I

ik + I

ji + I

jj + I

jk + I

ki + I

kj + I

kk (3.115)

The moments of inertia I

, I

, and I

are deﬁned as follows:



ρ(y

+ z

)dV



ρ(z

+ x

)dV (3.116)



ρ(x

+ y

)dV

where ρ is the mass density and dV is a volume element of the rigid body. The products of

inertia are deﬁned with a minus sign, that is,

= I

=−



ρxydV

= I

=−



ρxzdV (3.117)

= I

=−



ρyzdV

Dyadic operations

In general, the order of the dot product of a dyadic and a vector is important, that is,

A · b = b · A (3.118)

161 Dyadic notation

for an arbitrary vector b. On the other hand, for a symmetric dyadic such as the inertia

dyadic I, we ﬁnd that

I · ω = ω · I = H (3.119)

where ω is an arbitrary angular velocity and H is the angular momentum about the origin of

the body-axis frame. Notice that the dot product of a vector and a dyadic results in a vector

having a different magnitude and direction, in general.

The cross product of a dyadic and a vector results in another dyadic. Again, the order is

important, that is,

A × b = b × A (3.120)

in general.

The deﬁning equation for a unit dyadic is

U = ii + jj + kk (3.121)

where one can use any orthogonal set of unit vectors. For an arbitrary vector b we see that

U · b = b · U = b (3.122)

A deﬁning equation for the inertia dyadic of a rigid body is

I =



[

(

ρ · ρ

)

U − ρρ

]

dm (3.123)

where ρ = x i + yj + zk is the position vector of the mass element dm relative to the origin

of the body axes.

Consider next the time derivative of a dyadic. As an example, suppose a rigid body has

an angular velocity ω. Its inertia dyadic is

I =



i=1



j=1

(3.124)

where the unit vectors are mutually orthogonal and rotate with the body. Upon differentiation

with respect to time, we obtain

I =



i=1



j=1

(

+ I

) (3.125)

For a rigid body the moments and products of inertia are constant scalar quantities, so

= 0. Also,

= ω × e

(3.126)

=−e

× ω (3.127)

Hence we see that

I = ω × I − I × ω (3.128)

162 Kinematics and dynamics of a rigid body

As another example of the use of dyadic notation, one can write the rotation matrix C in

dyadic form. This rotation dyadic is

C = c



i + c



j + c



k + c



i + c



j + c



i + c



j + c



k (3.129)

The ﬁrst subscript and unit vector in each term refer to an axis of the new primed coordinate

system after rotation, while the second subscript and unit vector refer to an axis of the

original unprimed system. Then, corresponding to (3.1) and (3.4), we obtain



= C · r (3.130)

and

r = C

· r



(3.131)

In order to obtain the transformation equations relating the inertia dyadic of a rigid body

with respect to primed and unprimed reference frames, let us begin with (3.123) and note

that

ρ = C

· ρ



= ρ



· C (3.132)

ρ · ρ = ρ



· ρ



(3.133)

U = C

· U



· C (3.134)

where U



is the unit dyadic expressed in terms of primed unit vectors. We obtain

I = C

· I



· C (3.135)

or, conversely,



= C · I · C

(3.136)

3.3 Basic rigid body dynamics

Kinetic energy

In accordance with Koenig’s theorem, the kinetic energy of a rigid body is equal to the sum

of (1) the kinetic energy due to the translational velocity of the center of mass and (2) the

kinetic energy due to rotation about the center of mass. Thus,

T = T

+ T

rot

(3.137)

where

(3.138)

rot

ω · I

· ω (3.139)

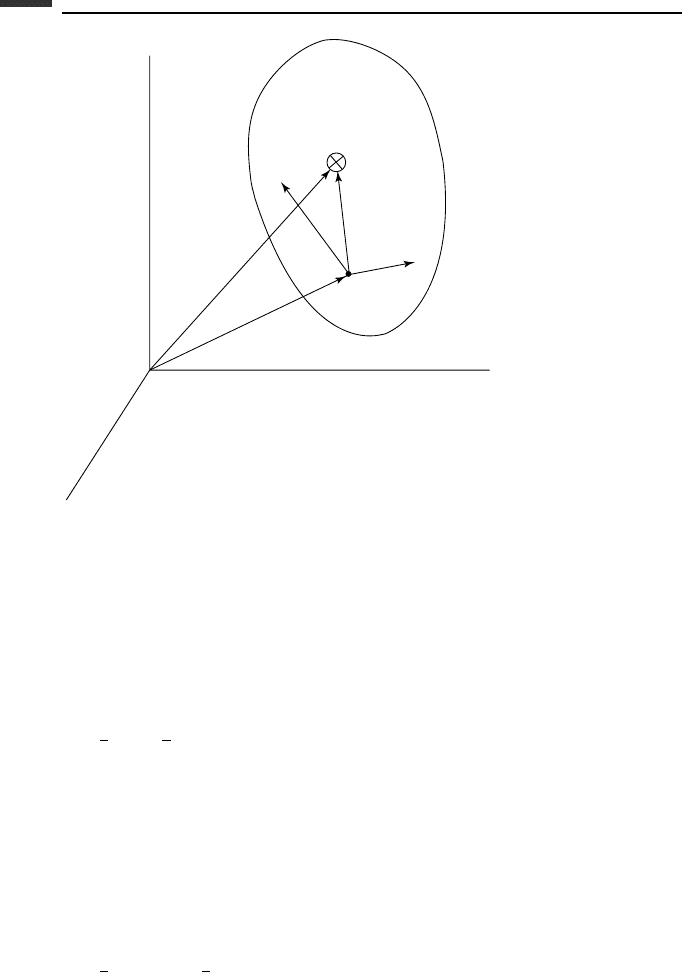
163 Basic rigid body dynamics

c.m.

rigid body

Figure 3.5.

Here v

is the velocity of the center of mass, I

is the inertia dyadic about the center of

mass, and ω is the angular velocity of the rigid body.

Frequently it is convenient to write the kinetic energy of a rigid body in terms of the

velocity of a reference point in the body. Suppose that a point P is ﬁxed in a rigid body

and moves with a velocity v. The position vector of the center of mass relative to P is ρ

(Fig. 3.5). Then, recalling (1.127), the kinetic energy of the rigid body is

T =

ω · I · ω + mv · ˙ρ

(3.140)

where the inertia dyadic I is taken about the reference point P.

Example 3.2 A comparison of methods for obtaining the kinetic energy of a system of

rigid bodies can be shown by considering the physical double pendulum of Fig. 3.6. Two

identical rigid bodies, supported by joints at A and B, move with planar motion. The bodies

each have mass m, length l, and moment of inertia I

about the center of mass.

In general, Koenig’s theorem applied to a system of N rigid bodies gives

T =



i=1



i=1

· I

· ω

(3.141)

164 Kinematics and dynamics of a rigid body

c.m.

(a)

c.m.

(b)

Figure 3.6.

First, consider Fig. 3.6a where absolute angular displacements are used. Noting that

= m

= m (3.142)

= I

(3.143)

= a

= l

+ a

+ 2al

cos(θ

− θ

) (3.144)

we obtain the total kinetic energy

T =

+ ma

)

+ ma

)

+ mal

cos(θ

− θ

) (3.145)

Another approach is to invoke (3.140) for a system of N rigid bodies, namely,

T =



i=1



i=1

· I

· ω



i=1

· ˙ρ

(3.146)

where v

is the velocity of the reference point of the ith body. In this case, we take reference

points at A and B, respectively, for the two bodies. The velocities of the reference points

are

= 0,v

= l

(3.147)

and the moments of inertia about the reference points are

= I

= I = I

+ ma

(3.148)

Noting that

˙ρ

= ω

× ρ

(3.149)

165 Basic rigid body dynamics

we obtain

T =





+ mal

cos(θ

− θ

) (3.150)

This result agrees with that obtained earlier in (3.145) but the use of (3.146) is somewhat

more direct. Thus, it is sometimes advantageous to use a reference point which is not at the

center of mass.

The kinetic energy expression can be used to ﬁnd the inertia coefﬁcients. They are given

∂

(3.151)

which results in

= I + ml

, m

= I, m

= m

= mal cos(θ

− θ

) (3.152)

Here m

is equal to the moment of inertia about A due to the ﬁrst body plus the mass of

the second body considered as a particle at B. Furthermore, m

is the moment of inertia

of the second body about its reference point B.

Now let us consider the case illustrated in Fig. 3.6b in which θ

is measured relative to the

ﬁrst body rather than having a ﬁxed reference. With the aid of (3.146), the kinetic energy is

found to be

T =

I (

)

+ mal

(

) cos θ

(2I + ml

+ 2mal cos θ

)

+ (I + mal cos θ

)

(3.153)

Then (3.151) yields

= 2I + ml

+ 2mal cos θ

, m

= I , m

= m

= I + mal cos θ

(3.154)

In this case, notice that m

is equal to the moment of inertia about A of the rigidly connected

bodies. Again, m

is equal to the moment of inertia of the second body about B.

Vectorial dynamics, Euler equations

The translational equation of motion for a rigid body has the vector form

ma = F (3.155)

where a is the acceleration of the center of mass and F is the total force acting on the body,

including any constraint forces. For a given total force acting on the body, this equation has

the same form as if the total mass m were concentrated as a particle at the center of mass.

Most of our attention, however, will be given to the rotational motion of a rigid body. A

fruitful approach is to use the vector equation

H = M (3.156)

166 Kinematics and dynamics of a rigid body

which applies if the reference point for the angular momentum H and the total moment M

acting on the body is either (1) ﬁxed or (2) at the center of mass. Let us choose a body-ﬁxed

coordinate system and let the reference point be at the origin O. The angular momentum is

H = I · ω (3.157)

or, in terms of body-axis components,

= I

+ I

= I

+ I

(3.158)

= I

+ I

Upon differentiation with respect to time, and referring to (3.128), we obtain

H = I · ˙ω +

I · ω

= I · ˙ω + (ω × I − I × ω) · ω

= I · ˙ω + ω × I · ω (3.159)

where we note that

(I × ω) ·ω = 0 (3.160)

From (3.156) and (3.159) we obtain

I · ˙ω + ω × I · ω = M (3.161)

Written in detail, we have the generalized Euler equations:

˙ω

+ I

(˙ω

− ω

) + I

(˙ω

+ ω

) + (I

− I

)ω

+ I



− ω



= M

(˙ω

+ ω

) + I

˙ω

+ I

(˙ω

− ω

) + (I

− I

)ω

+ I



− ω



= M

(˙ω

− ω

) + I

(˙ω

+ ω

) + I

˙ω

+ (I

− I

)ω

+ I



− ω



= M

(3.162)

These equations apply for an arbitrary orientation of the body axes relative to the rigid body.

Equations (3.161) or (3.162) can also be written in the matrix form

I ˙ω + ˜ωI ω = M (3.163)

where ˜ω is given by (3.61) and represents the cross product of ω.

Usually it is convenient to choose body axes which are also principal axes. Then the

products of inertia vanish and we obtain the familiar Euler equations:

˙ω

+ (I

− I

)ω

= M

˙ω

+ (I

− I

)ω

= M

(3.164)

˙ω

+ (I

− I

)ω

= M

Here the reference point for H and M is the origin O of the body-ﬁxed frame, and this

point is located at the center of mass or at an inertially ﬁxed point. If the applied moments

are known, these nonlinear ﬁrst-order differential equations can be integrated numerically

167 Basic rigid body dynamics

to give the ω components as functions of time. To obtain the orientation as a function of

time, the ωs are substituted into the kinematic equations (3.16) or (3.19) or (3.80), and these

are integrated numerically to give Euler angles or Euler parameters as functions of time.

As an extension of this vectorial approach to the rotational dynamics of a rigid body, let

us consider the case of a reference point P which is ﬁxed in the body, but it is neither at

the center of mass nor at a ﬁxed point in space. The angular momentum with respect to

P is

= I

· ω (3.165)

where I

is the inertia dyadic of the rigid body about P. The equation of motion corre-

sponding to (3.156) is

= M

− ρ

× m

(3.166)

in agreement with (1.115) which was obtained for a system of particles. The last term of

(3.166) can be interpreted as the moment about P due to an inertia force −m

acting

through the center of mass, and due to the acceleration of the reference point. Thus we

obtain

· ˙ω + ω × I

· ω + ρ

× m

= M

(3.167)

This result may be regarded as an extension of Euler’s equation for the case of an accelerating

reference point.

In general, the angular momentum H

about an arbitrary reference point P is equal to

the angular momentum H

about the center of mass plus the angular momentum due to the

translational velocity of the center of mass relative to the reference point. For this case in

which the reference point P is ﬁxed in the rigid body, we have (see Fig. 3.5)

= H

+ mρ

× ˙ρ

= H

+ mρ

× (ω × ρ

) (3.168)

Hence, we obtain

· ω = I

· ω + mρ

ω − m(ρ

· ω)ρ

= I

· ω + m



U − ρ



· ω (3.169)

Since ω is arbitrary, we see that

= I

+ m



U − ρ



(3.170)

where, in terms of body-axis components,

= x

i + y

j + z

k (3.171)

In detail, the moments and products of inertia about P due to a translation of axes are

= (I

)

+ m



+ z



= (I

)

+ m



+ x



(3.172)

= (I

)

+ m



+ y



168 Kinematics and dynamics of a rigid body

and

= (I

)

− mx

= (I

)

− mx

(3.173)

= (I

)

− my

We see that a translation of axes away from the center of mass always increases the moments

of inertia, but the products of inertia may increase or decrease.

Ellipsoid of inertia

Consider the kinetic energy of a rigid body rotating about a ﬁxed reference point. It is,

similar to (3.139),

T =

ω · I · ω (3.174)

where I is the inertia dyadic about the reference point and ω is the angular velocity vector.

An alternate expression for the kinetic energy due to rotation about a ﬁxed reference point

T =

I ω

(3.175)

where the scalar I is the moment of inertia about the axis of rotation and ω is the magnitude

of the angular velocity. This is apparent from (3.174) for the case where ω is directed along

one of the coordinate axes.

From (3.174) and (3.175) we obtain

ω · I · ω =

I ω

(3.176)

or, dividing by the right-hand side,

ρ · I · ρ = 1 (3.177)

where

ρ =

√

(3.178)

We see that ρ has the same direction as ω and a magnitude that is inversely proportional to

√

I or the radius of gyration. Suppose we consider ρ to be a vector drawn from the origin

of the body-ﬁxed frame to the point (x, y, z), that is,

ρ = xi + yj + zk (3.179)

Then, (3.177) takes the form

+ I

+ 2I

xy + 2I

xz + 2I

yz = 1 (3.180)

This is the equation of an ellipsoidal surface and is known as the ellipsoid of inertia.

The ellipsoid of inertia is ﬁxed relative to the rigid body and the body-ﬁxed frame. It is