Greenwood D.T. Advanced Dynamics

Подождите немного. Документ загружается.

179 Basic rigid body dynamics

The differential equations of rotational motion are obtained by using Lagrange’s equation

in the form



∂T

∂



−

∂T

∂q

= Q

(3.252)

These equations of motion are

sin

θ + (I

sin

φ + I

cos

φ) cos

θ]

ψ + (I

− I

)

θ cos θ sin φ cos φ

− I

φ sin θ + 2[I

− (I

sin

φ + I

cos

φ)]

θ sin θ cos θ

+ 2(I

− I

)

φ cos

θ sin φ cos φ + (I

− I

)

sin θ sin φ cos φ

+ [−I

+ (I

− I

)(cos

φ − sin

φ)]

φ cos θ = Q

− I

)

ψ cos θ sin φ cos φ + (I

cos

φ + I

sin

φ)

− [I

− (I

sin

φ + I

cos

φ)]

sin θ cos θ

+ [I

+ (I

− I

)(cos

φ − sin

φ)]

φ cos θ + 2(I

− I

)

φ sin φ cos φ = Q

(3.253)

− I

ψ sin θ + I

φ + (I

− I

)

cos

θ sin φ cos φ

− [I

+ (I

− I

)(cos

φ − sin

φ)]

θ cos θ

+ (I

− I

)

sin φ cos φ = Q

In accordance with the virtual work approach to ﬁnding generalized forces, we see that

a total applied moment M is associated with a virtual work

δW = M · e

δψ + M · e

δθ + M · e

δφ (3.254)

where es are unit vectors in the directions of the respective rotation axes (Fig. 3.2). Thus,

= M · e

, Q

= M · e

, Q

= M · e

(3.255)

The three second-order differential equations given in (3.253) are relatively complicated.

Furthermore, they must be solved for the individual accelerations

ψ,

θ, and

φ before being

integrated numerically. This involves an inversion of the mass matrix m. By comparison,

the use of the three ﬁrst-order Euler equations given in (3.164) to solve for ω

, ω

, and ω

followed by the three ﬁrst-order kinematic equations of (3.16) to obtain the Euler angles ψ,

θ, and φ, appears to be much simpler.

The use of type II Euler angles and Lagrange’s equation would result in equally compli-

cated equations of motion.

Angular velocity coefﬁcients

The state of motion of the i th rigid body can be expressed by giving the velocity v

of a

reference point P

ﬁxed in the body and also giving its angular velocity ω

. In terms of

qs,

180 Kinematics and dynamics of a rigid body

the velocity v

can be written in the form



j=1

(q, t)

+ γ

(q, t) (3.256)

as in (1.43). The γs are called velocity coefﬁcients and, in particular, γ

is a vector coefﬁcient

representing the sensitivity of the reference point velocity v

to changes in

In a similar manner, the angular velocity ω

of the ith body can be expressed as



j=1

(q, t)

+ β

(q, t) (3.257)

where the βs are called angular velocity coefﬁcients.

We see that

∂v

∂

(3.258)

and

∂ω

∂

(3.259)

Furthermore, for the case of a scleronomic system, we ﬁnd that all γ

and all β

are equal

to zero.

Now, let us consider virtual work as it applies to a rigid body. An arbitrary set of forces

acting on the ith body is dynamically equivalent to a total force F

acting at the reference

point plus a couple of moment M

which may be applied anywhere on the body. The virtual

work of this force system due to an arbitrary virtual displacement is

δW

= F

· δr

+ M

· δθ

(3.260)

where δr

is a small displacement of the reference point and δθ

represents a small rotation

of the body. Now

δr



j=1

δq

(3.261)

and

δθ



j=1

δq

(3.262)

Therefore, for the ith body,

δW



j=1

· γ

+ M

· β

)δq

(3.263)

For a system of N rigid bodies, the total virtual work is

δW =



i=1

δW



i=1



j=1

· γ

+ M

· β

)δq

(3.264)

181 Basic rigid body dynamics

Thisisoftheform

δW =



j=1

δq

(3.265)

where the generalized force associated with q



i=1

· γ

+ M

· β

)(j = 1,...,n) (3.266)

As an illustration of the meaning of the βs in (3.266), consider a rigid body whose

orientation is given by three Euler angles, as in Example 3.6 on page 178. Referring to

(3.255), we see that

= e

, β

= e

, β

= e

(3.267)

where the es are unit vectors in the directions of the respective rotation axes. In general,

however, the angular velocity coefﬁcients need not be of unit magnitude.

We have deﬁned the velocity coefﬁcients and angular velocity coefﬁcients with respect to

true velocities (

qs), but one can also deﬁne these coefﬁcients with respect to quasi-velocities.

Thus, when using quasi-velocities (us) as velocity variables, we write

∂v

∂u

(3.268)

∂ω

∂u

(3.269)

Furthermore, we ﬁnd that



j=1

(q, t)u

+ γ

(q, t) (3.270)



j=1

(q, t)u

+ β

(q, t) (3.271)

The generalized force Q

associated with u

is given by (3.266) where the γs and βsare

obtained from (3.268) and (3.269).

If the velocity variables are a mixture of quasi-velocities and true velocities, one can use

quasi-velocity notation and identify some of the us with

qs as a special case of (3.245).

Free rotational motion

The rotational motion of a rigid body is free if the system of applied forces results in a

zero moment about the reference point which is inertially ﬁxed or at the center of mass.

Our approach to solving for the free rotational motion will be to use integrals of the motion

directly, rather than starting with second-order differential equations.

Let us represent the orientation of the body by type II Euler angles (Fig. 3.3). Since there

are no applied moments, the angular momentum is constant in magnitude and direction. Let

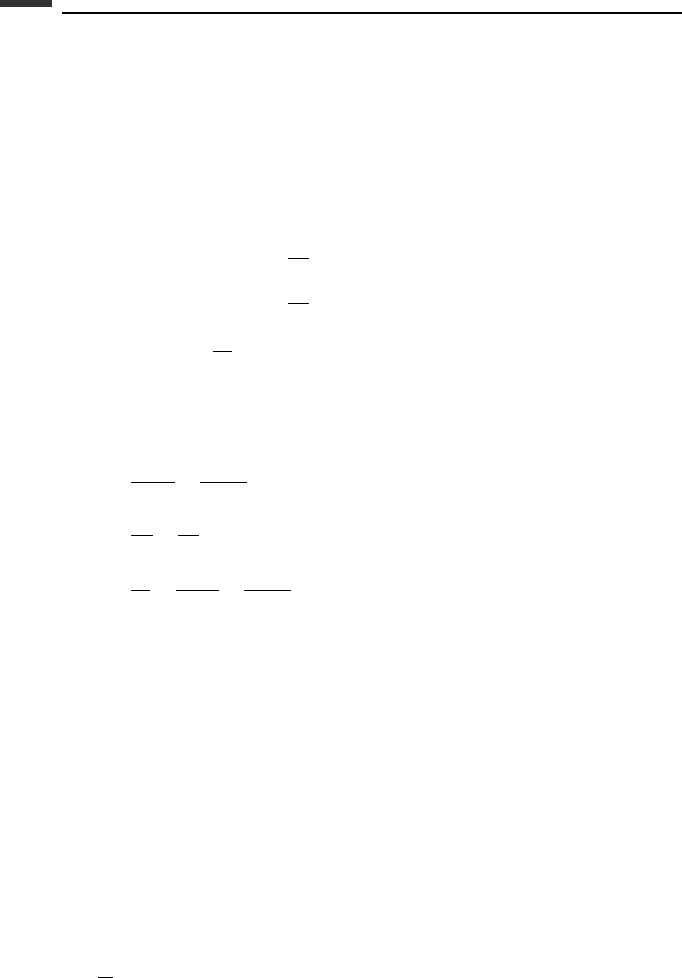
182 Kinematics and dynamics of a rigid body

us deﬁne the vertical direction as the direction of the H vector, that is, H can be considered

to lie along the positive Z -axis. Then, assuming that the xyz body axes are principal axes,

we see from the geometry that

= I

= H sin θ sin ψ (3.272)

= I

= H sin θ cos ψ (3.273)

= I

= H cos θ (3.274)

where H is a positive constant. Thus, we obtain

φ sin θ sin ψ +

θ cos ψ =

sin θ sin ψ (3.275)

φ sin θ cos ψ −

θ sin ψ =

sin θ cos ψ (3.276)

φ cos θ +

ψ =

cos θ (3.277)

These three equations represent the integrals of the motion; that is, we can write three

independent functions of the qs and

qs which are equal to zero. Finally, solving (3.275)–

(3.277) for the type II Euler angle rates, we obtain

φ = H



sin

cos



(3.278)

θ = H



−



sin θ sin ψ cos ψ (3.279)

ψ = H



−

sin

−

cos



cos θ (3.280)

Note that the precession rate

φ is always positive, but the nutation rate

θ and the relative

spin

ψ may have either sign. If the z-axis is an axis of either maximum or minimum moment

of inertia, we ﬁnd that 0 ≤ θ ≤ π/2 for any physically realizable body. If I

is the minimum

moment of inertia,

ψ is positive; if I

is maximum, then

ψ is negative.

Axial symmetry

Now suppose that the body-ﬁxed z-axis is a symmetry axis. Let

= I

, I

= I

(3.281)

First, we note from (3.279) that

θ = 0orθ = const (3.282)

From (3.278), the constant precession rate is

φ =

(3.283)

183 Basic rigid body dynamics

The relative spin rate, from (3.280), is also constant, that is,

ψ = H



−



cos θ (3.284)

where

H =



cos θ

(3.285)

and the total spin  is

 = ω

φ cos θ +

ψ (3.286)

which is constant. Thus, we ﬁnd that

ψ =



1 −



 (3.287)

For the prolate case (I

< I

) we ﬁnd that

ψ is positive; whereas, for the oblate case

> I

ψ is negative. Here we take the positive direction of the symmetry axis in this

free motion so that the total spin  is always positive or zero.

Notice that, since θ is constant, the symmetry axis will sweep out a conical surface as it

precesses about the H vector which lies on the Z-axis. This is called a coning motion and

is typical of the free rotational motion of an axially-symmetric body.

The Poinsot method

The Poinsot method is a geometrical method of representing the free rotational motion of

a rigid body. It is exact and is based upon the conservation of angular momentum and of

kinetic energy.

Let us choose a set of principal axes at the center of mass as the xyz body-ﬁxed frame.

Then, if I

, I

, and I

are the principal moments of inertia, (3.180) representing the ellipsoid

of inertia reduces to

+ I

= 1 (3.288)

The Poinsot construction (Fig. 3.9) pictures the free rotational motion of a rigid body

as the rolling of its ellipsoid of inertia on an invariable plane which is perpendicular to

the constant angular momentum vector H drawn from the ﬁxed center O. To see how this

comes about, recall from (3.178) that the vector ρ from O to P is

ρ =

√

(3.289)

Also, from (3.176) we note that the rotational kinetic energy is

rot

ω · H =

I ω

(3.290)

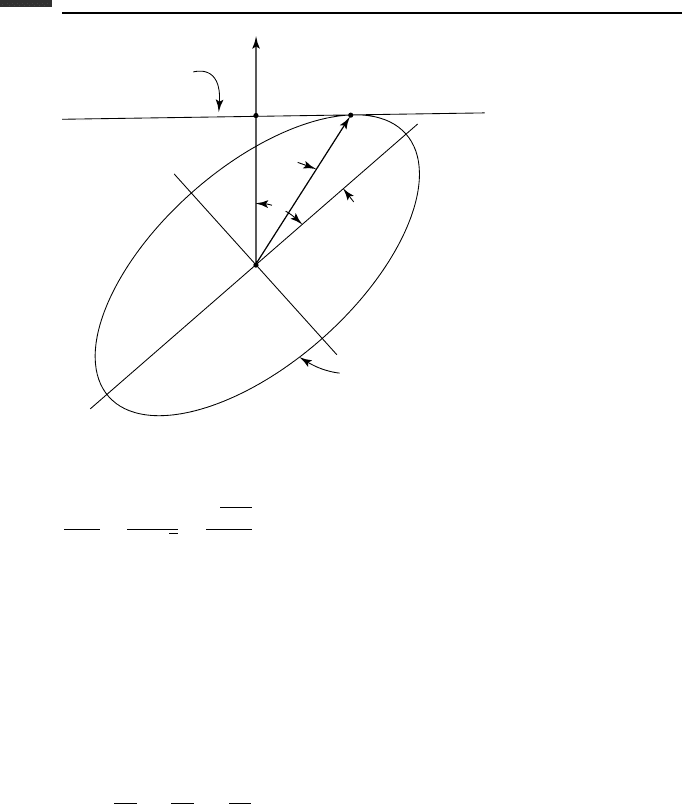
184 Kinematics and dynamics of a rigid body

invariable

plane

ellipsoid

of inertia

Figure 3.9.

Thus, we ﬁnd that the length OS is

ρ · H

ω · H

ωH

√

rot

(3.291)

which is constant as P moves. This means that the point P moves in a plane that is

perpendicular to the angular momentum vector H and intersects it at S. This plane is ﬁxed

in space and is known as the invariable plane.

Next, we need to show that the invariable plane is tangent to the inertia ellipsoid at P.

The ellipsoid has the form

F(x , y, z) = I

+ I

= 1 (3.292)

The direction of the normal to the ellipsoid at P is found by evaluating the gradient ∇F at

that point. Now

∇F =

∂ F

∂x

i +

∂ F

∂y

j +

∂ F

∂z

= 2I

xi + 2I

yj + 2I

zk (3.293)

We see that ∇F is parallel to H since

H = I

i + I

j + I

k (3.294)

and

: ω

= x : y : z (3.295)

185 Basic rigid body dynamics

that is, ω and ρ have the same direction in space. We conclude that the invariable plane is

tangent to the inertia ellipsoid at P. The instantaneous axis of rotation passes through the

contact point P, so the ellipsoid of inertia rolls without slipping on the invariable plane.

Because ω has a component normal to the invariable plane, there is also some pivoting

about P. Of course, the actual rigid body goes through the same rotational motions as the

ellipsoid of inertia.

It is interesting to consider the path of the contact point P on both the invariable plane

and the inertia ellipsoid. The path of P on the invariable plane is called the herpolhode.It

is not a closed curve, in general, as P moves continuously between two circles centered on

S and corresponding to extreme values of (θ − α). During successive intervals of π/2in

ψ, P moves from tangency with one circle to tangency with the other.

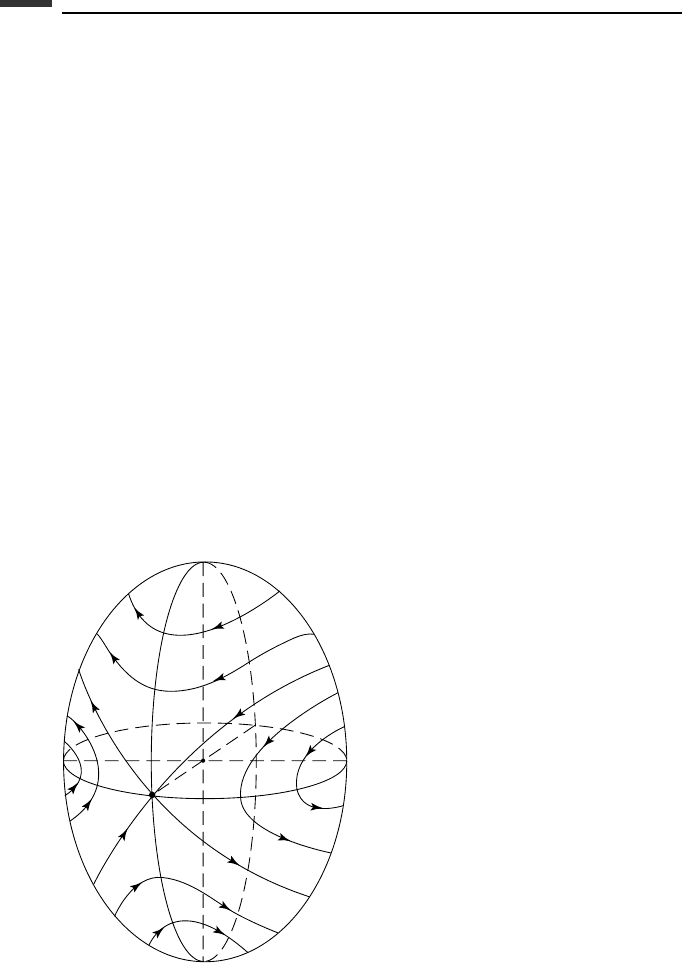
The curve traced by P on the ellipsoid of inertia is called a polhode. For any rotation

not exactly about a principal axis, the polhode curves are closed and encircle either the

axis of minimum moment of inertia Ok or the axis of maximum moment of inertia On

(Fig. 3.10).

The polhode curves are formed by the intersection of two ellipsoids, namely, the inertia

ellipsoid and the momentum ellipsoid. The inertia ellipsoid relative to principal axes was

given by (3.288). To obtain the momentum ellipsoid we start with the expression for the

square of the angular momentum.

+ I

= H

(3.296)

Figure 3.10.

186 Kinematics and dynamics of a rigid body

However, from (3.289) and (3.290) we see that

= x ω

√

I = x



rot

= yω

√

I = y



rot

(3.297)

= zω

√

I = z



rot

Hence we obtain the momentum ellipsoid

+ I

rot

= D (3.298)

where H and T

rot

are constants which are usually evaluated from the initial conditions.

The polhode curve for a given case of free rotational motion is determined by the values of

(x , y, z) satisfying the initial value of ρ as well as (3.288) and (3.298). It can be shown that

if D < I

, assuming I

< I

, the polhode encircles the axis Ok corresponding to the

minimum moment of inertia. If D > I

, the polhode encircles the axis On corresponding

to the maximum moment of inertia.

Now consider the stability of rotational motion about a principal axis. The polhodes in

the vicinity of k and n are tiny ellipses indicating stability, that is, a small displacement

of the axis of rotation relative to the body will remain small. On the other hand, polhodes

near m are hyperbolic in nature, indicating instability. The axis of rotation relative to the

body will suddenly ﬂip over to nearly the opposite direction and then return back again,

only to repeat the cycle. Meanwhile the angular momentum vector H remains constant in

space. Thus the rotational motion of the body in space is quite irregular. In theory it takes

an inﬁnite time for the point P to leave m but, practically speaking, there are enough small

disturbances that the instability of rotational motion about the intermediate axis Om is

immediately apparent.

The above analysis has assumed an ideal rigid body without internal losses. However,

an actual body will have structural damping with some energy loss due to slight elastic

deﬂections during the motion. As a result, there will be a decline in kinetic energy consistent

with the constant angular momentum. Finally, there will be a steady rotational motion about

the axis On corresponding to the maximum moment of inertia and minimum kinetic energy.

This explains why a spin-stabilized rigid body in space must rotate about its axis of maximum

moment of inertia.

Axial symmetry

Now assume an axially-symmetric rigid body is undergoing free rotational motion. In this

case the inertia ellipsoid is an ellipsoid of revolution and the polhodes are circles centered

on the axis of symmetry. First consider the case in which Ok of Fig. 3.10 is the axis of

symmetry and I

= I

, I

= I

and I

< I

, that is, the axis of symmetry corresponds

to the minimum moment of inertia. The inertia ellipsoid is a prolate spheroid and, as it rolls

on the invariable plane, the ω vector sweeps out a cone relative to the body and also a cone

in space. This is conveniently represented by a body cone rolling on the outside of a ﬁxed

space cone (Fig. 3.11a). Notice that the symmetry axis Oz and the angular velocity vector

187 Basic rigid body dynamics

body cone

< I

space cone

(a)

body cone

> I

space

cone

(b)

Figure 3.11.

ω lie on the same side of the angular momentum vector H. Also the precession rate

φ is

smaller than ω.

If, on the other hand, the axis of symmetry corresponds to the maximum moment of

inertia, the inertia ellipsoid is an oblate spheroid and we can take I

= I

, I

= I

with I

> I

. Again the polhodes are circles and, in this case, the axis of symmetry is On.

Because of the oblateness, the symmetry axis and the ω vector lie on opposite sides of the

H vector. This leads to the rolling cone model shown in Fig. 3.11b in which the inside of

the body cone rolls on the outside of the ﬁxed space cone. Usually the precession rate

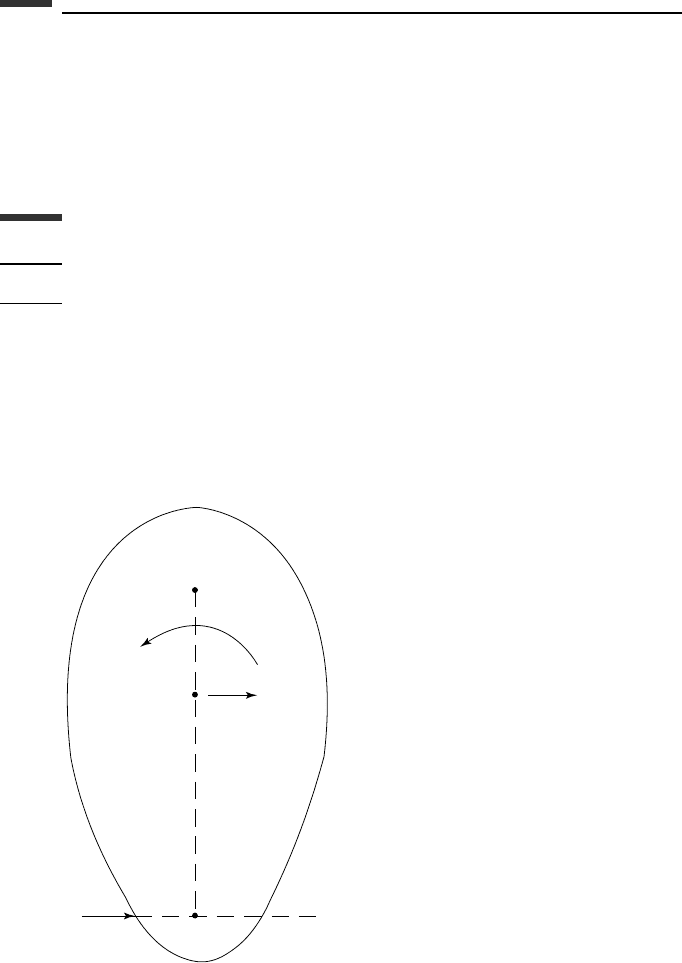
188 Kinematics and dynamics of a rigid body

is larger than ω. In both the prolate and oblate cases the rolling cone model gives an exact

representation of the free rotational motion of an axially symmetric body.

From Fig. 3.11 we see that, for a given angular velocity ω, the precession rate

φ for the

prolate case is smaller than for the oblate case. Furthermore, notice that the relative spin

rate

ψ is positive, that is, in the direction of the symmetry axis Oz for the prolate case but

ψ is negative for an oblate body. This is in agreement with (3.287).

3.4 Impulsive motion

Planar rigid body motion

Let us begin with the relatively simple case of the planar impulsive response of a rigid

body. Suppose an impulse

F is applied to a rigid body along one of its principal planes.

The response will be the same as if

F were applied to a lamina having the same mass m

and moment of inertia I about the center of mass C (Fig. 3.12).

Assume that the lamina is initially motionless. An impulse

F is applied with a line of

action through B and perpendicular to the line AB that passes through the center of mass.

The principle of linear impulse and momentum is used to obtain the velocity v of the center

Figure 3.12.