Greenwood D.T. Advanced Dynamics

Подождите немного. Документ загружается.

209 Problems

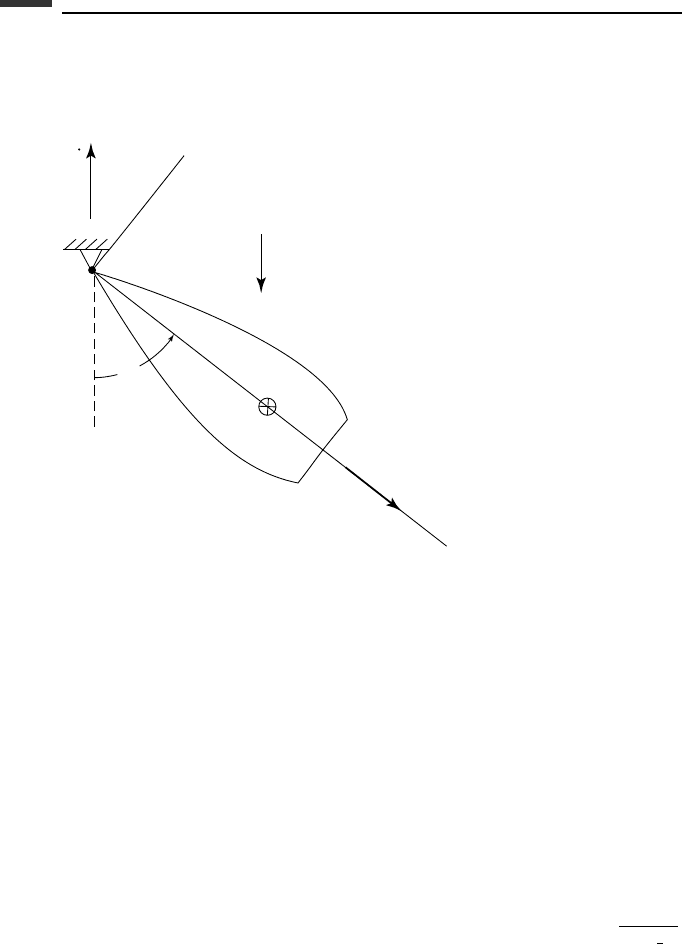
and the xy-plane is vertical. (a) Find the θ and φ differential equations of motion. (b)

Assume the initial conditions θ (0) = 60

◦

θ(0) =

φ(0) = 0, ω

(0) =  and solve for

the minimum value of θ during the motion. Assume that I



= 2I

mgl.

c.m.

Ω

Figure P 3.10.

3.11. A rigid body with xyz principal body axes is suspended by a massless gimbal system

associated with type I Euler angles. The outer gimbal can rotate freely about the

vertical ψ-axis. Assume that the inner gimbal is locked relative to the outer gimbal,

and the Euler angle θ is constant. A motor drives the rigid body relative to the inner

gimbal and produces a constant moment Q

about the x-axis. Assume axial symmetry,

that is, I

= I

, I

= I

. (a) Write the differential equations of motion. (b)

Show that the vertical angular momentum is constant, even though Q

has a vertical

component. Explain.

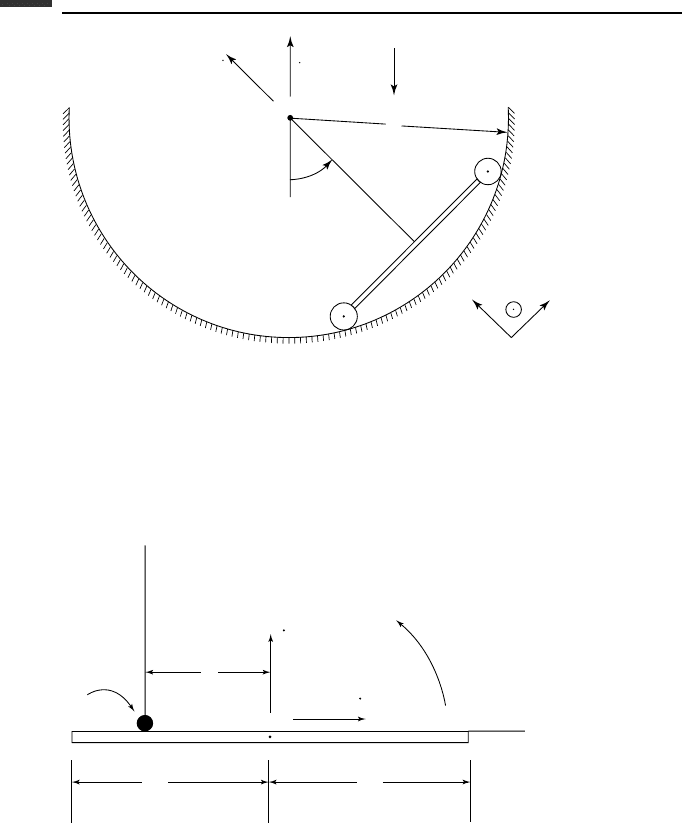
3.12. A dumbbell consists of particles A and B, each of mass m, connected by a massless

rigid rod of length l (Fig. P 3.12). It can slide without friction on a ﬁxed spherical

depression of radius r under the inﬂuence of gravity. The conﬁguration of the system

is given by the type II Euler angles (φ,θ,ψ), where ψ is the angle between the rod

AB and the vertical plane which includes the center O and the center of mass. Note

that the center of mass of the dumbbell moves on a sphere of radius R =



−

Obtain the equations of motion using the Lagrangian method.

210 Kinematics and dynamics of a rigid body

–

Figure P 3.12.

3.13. A rod of mass m and length l is in general planar motion when it has inelastic impact

withasmoothﬁxedpegP at a distance a from the center. The initial conditions just

before impact are

x(0) =

y(0) =

, ω(0) = ω

. Solve for the velocity components

(

y) of the center of mass as well as the angular velocity ω just after impact.

peg

–

Figure P 3.13.

3.14. The angles (θ,φ) describe the orientation of a uniform rod of mass m and length

l which is spinning with one end in contact with a smooth ﬂoor (Fig. P 3.14). (a)

Use the Routhian method to obtain a differential equation of the form

θ(θ,

θ) = 0.

(b) Assume the initial conditions θ (0) = 45

◦

θ(0) = 0,

φ(0) = ω

and solve for the

initial value of the ﬂoor reaction N .

211 Problems

–

Figure P 3.14.

3.15. An axially-symmetric top with mass m, and with axial and transverse moments of

inertia I

and I

, respectively, about the center of mass has a total spin rate  about its

symmetry axis. Its center of mass is located at a distance l from its point O which can

slide without friction on a horizontal ﬂoor. (a) Use type I Euler angles as coordinates

and the modiﬁed Euler equations to obtain the θ and ψ equations of motion. (b) Let

= ml

/12, I

= ml

/6, and 

= 72g/l. Assume that the top is initially vertical

and is disturbed slightly. Solve for θ

min

in the motion which follows. (c) What is the

precession rate

ψ when θ = θ

min

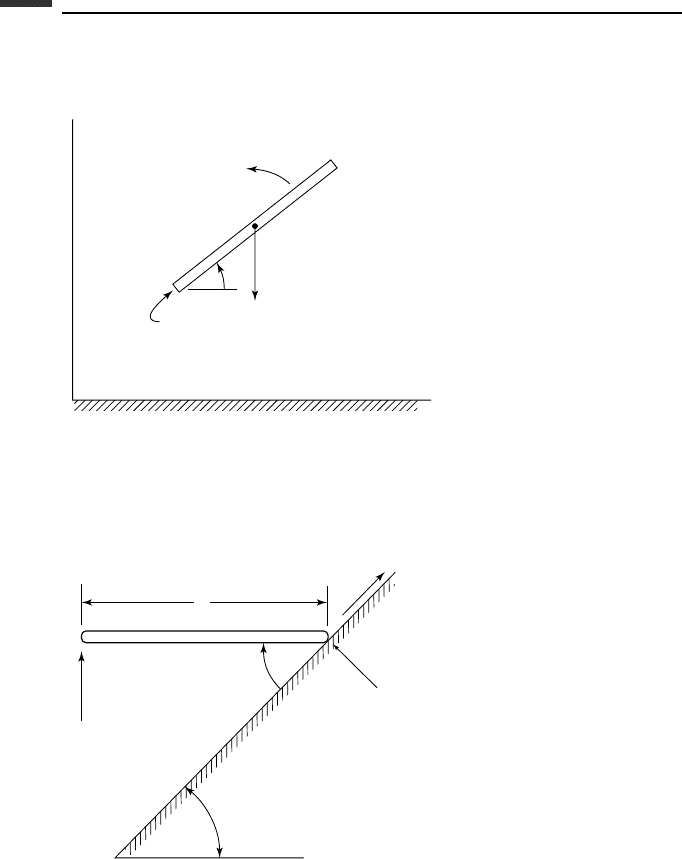
3.16. Two thin disks, each of mass m and radius r , are connected by a thin rigid axle of

mass m

and length L, and roll without slipping on the horizontal xy-plane. (a) Using

(v,

φ) as velocity variables, ﬁnd the kinetic energy and the mass matrix. (b) If the

system is initially at rest, solve for v and

φ due to a transverse horizontal impulse

which is applied to the axle at a distance c from its center.

Ω

–

Figure P 3.16.

212 Kinematics and dynamics of a rigid body

3.17. A rod of mass m and length l is dropping vertically with speed v

and angular velocity

, when end A hits a smooth ﬂoor inelastically at y = 0. Solve for the values of

and

θ immediately after impact, as well as the constraint impulse.

(x, y)

Figure P 3.17.

3.18. A uniform rod of mass m and length l is at rest with θ = 45

◦

and end B touching

a smooth plane surface. Then a transverse impulse

F is applied at end A. (a) Solve

for u

and u

≡

θ immediately after the impulse. (b) Find the value of the constraint

impulse

C. End B remains in contact with the plane.

45°

Figure P 3.18.

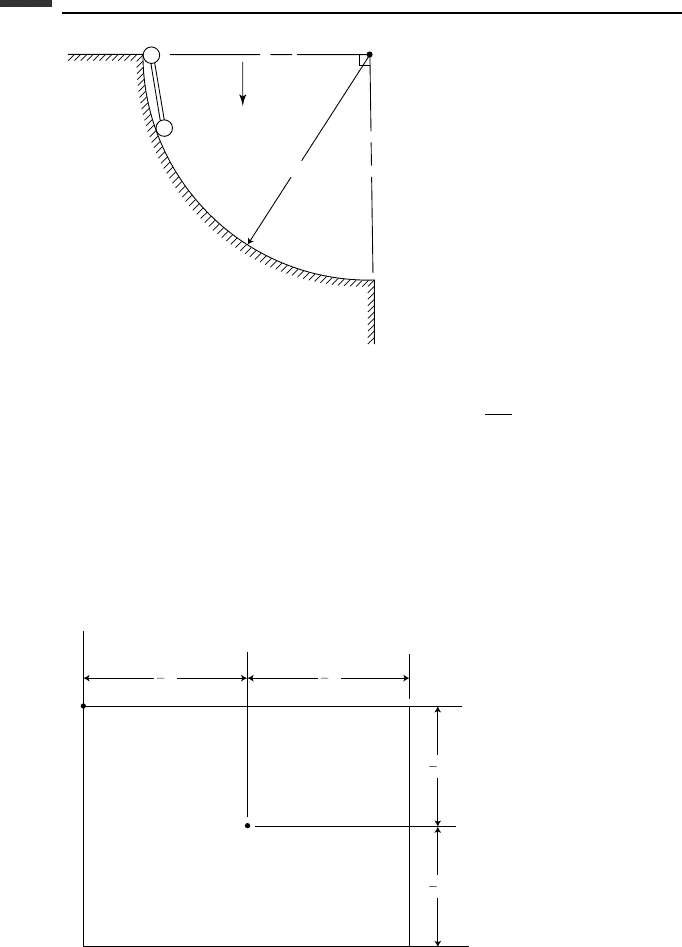
3.19. A dumbbell is released from the position shown in Fig. P 3.19 and slides without

friction down a circular track of radius R. Assume that the dumbbell length l << R

and keep terms to ﬁrst order in l/R. Find the angular velocity of the dumbbell when:

(a) particle 1 leaves the track; (b) particle 2 leaves the track.

213 Problems

Figure P 3.19.

3.20. A thin disk of mass m and radius r is spinning at ω

√

g/r about a vertical diameter

on a frictionless ﬂoor. Then it is disturbed slightly. (a) Find the maximum value of the

angle θ between the plane of the disk and the vertical in the motion which follows.

(b) What is the minimum value of ω

for stability of the initial motion?

3.21. A thin horizontal rectangular plate is translating downward (into page) with a velocity

when its corner A is suddenly stopped at a ﬁxed point. Assuming the rigid plate

can rotate freely about A, solve for its angular velocity ω and the velocity v

of its

center immediately after impact.

Figure P 3.21.

214 Kinematics and dynamics of a rigid body

3.22. A dumbbell is composed of two smooth spheres, each of mass m, radius r, and central

moment of inertia I

. They are connected by a rigid massless rod of length

L. Just before perfectly elastic impact the dumbbell has a longitudinal velocity v

an angle 45

◦

relative to the ﬂoor. (a) Solve for the velocities of the two spheres just

after impact. (b) What is the angular impulse applied to sphere 1 about its center? (c)

Solve for the shear impulse normal to the rod.

e = 1

45°

Figure P 3.22.

3.23. A system consists of three rods, each of mass m and length l, which are connected by

joints at B and C. The system is initially motionless with θ

= θ

= 45

◦

and θ

= 0

when the velocities v

and v

are suddenly applied, as shown. Solve for the resulting

immediate values of

and

Figure P 3.23.

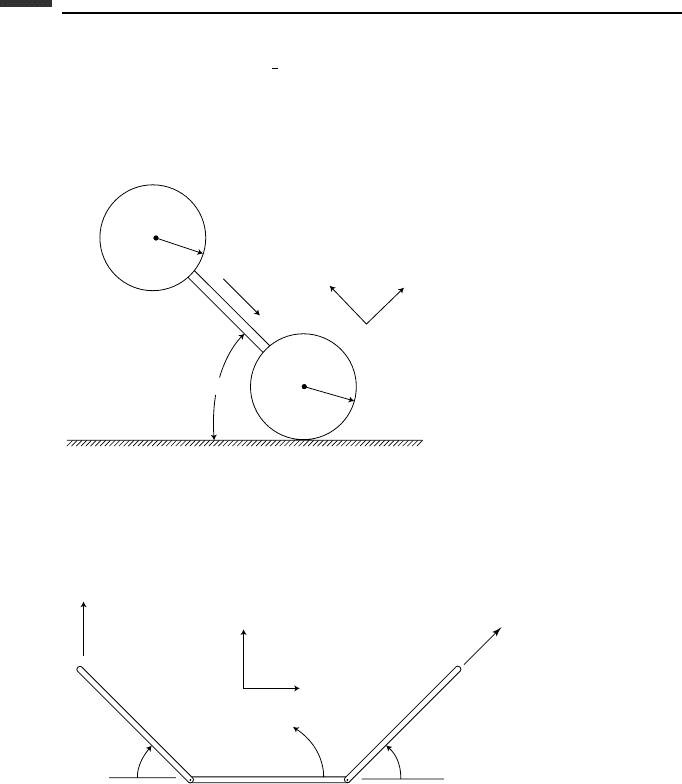
3.24. A uniform rod of mass m and length l has a ﬁxed spherical joint at end B (Fig. P 3.24).

End C rests against a vertical wall having a friction coefﬁcient µ. The rod can rotate

with a constant angle α about a horizontal axis AB which is perpendicular to the wall.

(a) Obtain the differential equation for the position angle θ. (b) Assume µ =0,α =

◦

with the initial conditions θ(0) = 0,

θ(0) = 0. The rod is disturbed slightly

in the positive θ direction. Solve for the angle θ at which the rod leaves the wall.

215 Problems

Figure P 3.24.

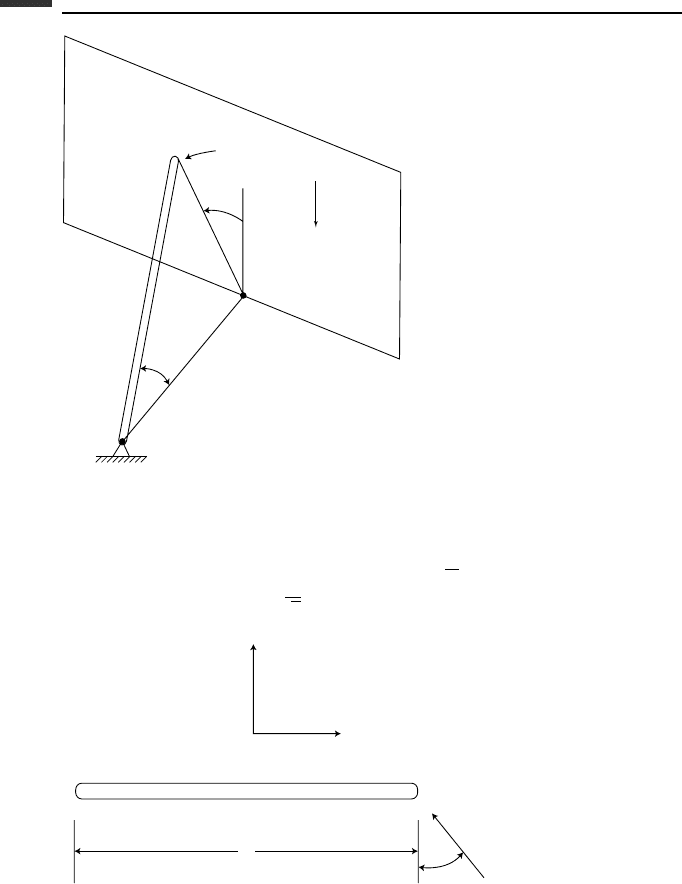
3.25. End B of a uniform rod of mass m and length l is initially at rest and then is hit

by an impulse

F at an angle α from the transverse direction, as shown. (a) Find the

resulting velocity at B and the driving-point mass

m associated with

F. (b) Show that

the kinetic energy is T =

Figure P 3.25.

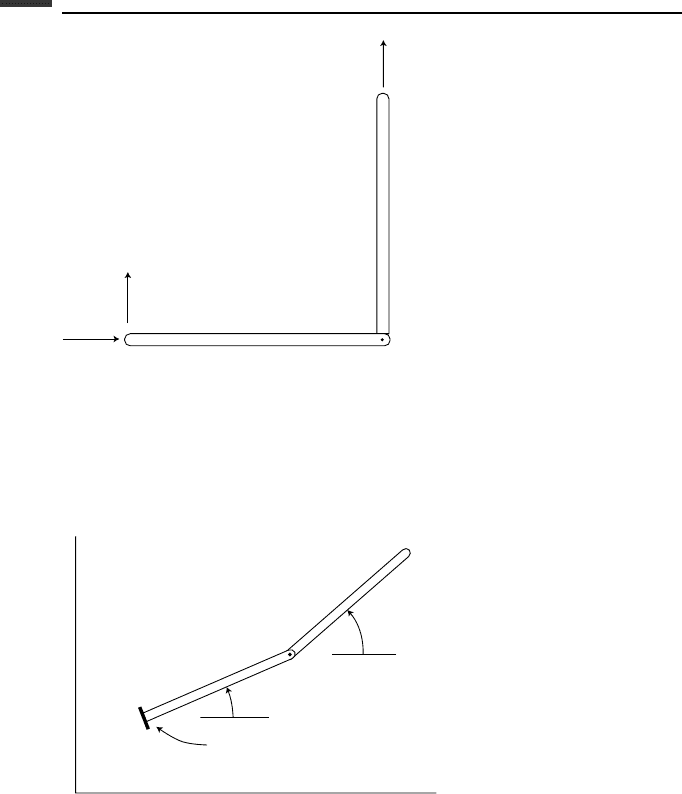
3.26. Find the input mass at A for the directions u

and u

(Fig. P 3.26). There is a pin joint

at B connecting the two rods.

216 Kinematics and dynamics of a rigid body

Figure P 3.26.

3.27. Two rods, each of mass m and length l are connected by a joint at B and move in a

horizontal plane. A knife-edge constraint requires that any motion at A be perpen-

dicular to the rod. Choose (x, y,θ

,θ

) as generalized coordinates and obtain three

second-order differential equations of motion by using Jourdain’s principle.

(x, y)

Figure P 3.27.

Equations of motion: differential approach

In the previous chapters, we have considered relatively familiar methods of obtaining the

differential equations of motion for a mechanical system. In this chapter, we shall introduce

a number of other methods, partly in order to give the student a broader view of dynamics,

and partly to present some practical and efﬁcient approaches to obtaining the differential

equations of motion. The results presented here are applicable to holonomic and nonholo-

nomic systems alike, but the emphasis will be on nonholonomic systems because greater

insight is needed in ﬁnding applicable theoretical approaches for these systems. As we pro-

ceed, we will show the advantages of using quasi-velocities in the analysis of nonholonomic

systems.

4.1 Quasi-coordinates and quasi-velocities

Transformation equations

It is often possible to simplify the analysis of dynamical systems by using quasi-velocities

(us) rather than

qs as velocity variables. An example is the use of Euler’s equations for

the rotational motion of a rigid body. Here the velocity variables are the body-axis com-

ponents of the angular velocity ω rather than Euler angle rates. The ω components are

quasi-velocities, whereas the Euler angle rates are true

qs whose time integrals result in

generalized coordinates. As we showed in Chapter 3, the Euler equations are simpler than

the corresponding Lagrange equations written in terms of Euler angles and Euler angle

rates.

The transformation equations relating the us and

qs can be obtained by starting with the

differential form

dθ



i=1



(q, t) dq

+ 

(q, t) dt ( j = 1,...,n) (4.1)

where the θs are called quasi-coordinates and dθ

= u

dt or u

. In general, the right-

hand expressions in (4.1) are not integrable; if they were integrable, the θswouldbetrue

generalized coordinates.

218 Equations of motion: differential approach

If (4.1) is divided by dt, it has the form



i=1



(q, t)

+ 

(q, t)(j = 1,...,n) (4.2)

as in (3.245). We assume that these n equations can be solved for the

qs, resulting in



j=1



(q, t)u

+ 

(q, t)(i = 1,...,n) (4.3)

Notice that for this unconstrained case, there are the same number of us and

qs. For

example, the rotational dynamics of a rigid body might have ω

,ω

as us and the Euler

angles ψ, θ, φ as qs. The dynamical equations would be written in terms of us and then the

qs would be generated by integrating (4.3) which are kinematic equations.

Constraints

Now let us impose m nonholonomic constraints of the linear form



i=1

(q, t)

+ a

(q, t) = 0(j = 1,...,m) (4.4)

as in (1.15). This will be accomplished by changing the notation and setting the last mus

in (4.2) equal to zero. Thus, we can write



i=1



(q, t)

+ 

(q, t)(j = 1,...,n − m) (4.5)



i=1



(q, t)

+ 

(q, t) = 0(j = n − m + 1,...,n) (4.6)

The ﬁrst (n − m) usareindependent quasi-velocities, while the last mus are set equal to

zero to enforce the m nonholonomic constraints.

As before, we assume that the (n × n) Ψ matrix is invertible and we can solve for the

in the form

n−m



j=1



(q, t)u

+ 

(q, t)(i = 1,...,n) (4.7)

The upper limit on the summation is (n − m) because the last mus are equal to zero. Note

that the (n × n) matrix Φ is

Φ = Ψ

−1

(4.8)

Furthermore,



=−



j=1





(i = 1,...,n) (4.9)

If there are any holonomic constraints, we have