Greenwood D.T. Advanced Dynamics

Подождите немного. Документ загружается.

239 The general dynamical equation

␾

␪

⍀

⭈

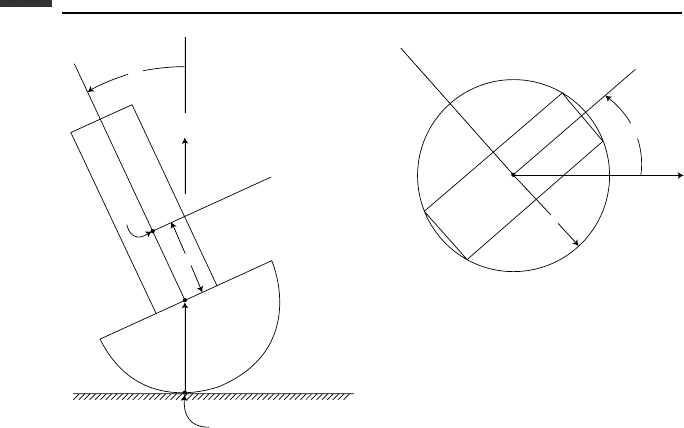
Figure 4.4.

Example 4.5 We can illustrate the use of (4.144) by considering the motion of a top with a

ﬁxed point O (Fig. 4.4). Let us use the type II Euler angles φ and θ to specify the orientation

of the xyz reference frame and its corresponding unit vectors i, j, k.

For quasi-velocities, let us choose

φ, u

θ, u

=  (4.147)

where the ﬁrst two are actually the time derivatives of true coordinates, and  is the total

angular velocity about the axis of symmetry z. The angular velocity of the xyz reference

frame is

θi +

φ sin θ j +

φ cos θ k (4.148)

whereas the angular velocity of the body is

ω =

θi +

φ sin θ j + k (4.149)

The angular velocity of the body relative to the xyz frame is the Euler angle rate

ψ, that is,

 =

φ cos θ +

ψ (4.150)

All the γ

velocity coefﬁcients are zero because the reference point O is ﬁxed. The βs

are

∂ω

∂

= sin θ j, β

∂ω

∂

= i, β

∂ω

∂

= k (4.151)

The angular momentum about O is

H = I

i + I

j + I

k = I

θi + I

φ sin θ j + I

k (4.152)

240 Equations of motion: differential approach

The xyz frame rotates at ω

i = ω

× i =

φ cos θ j −

φ sin θ k

j = ω

× j =−

φ cos θ i +

θk

k = ω

× k =

φ sin θ i −

θj

(4.153)

Thus, we ﬁnd that

H = (I

θ − I

sin θ cos θ + I



φ sin θ )i

+(I

φ sin θ + 2I

θ cos θ − I



θ) j + I

k (4.154)

The Qsare

= Q

= 0, Q

= Q

= mgl sin θ, Q

= Q



= 0 (4.155)

The general dynamical equation in the form of (4.144) is used to obtain, ﬁrst, the φ

equation from the j component of

φ sin

θ + 2I

θ sin θ cos θ − I



θ sin θ = 0 (4.156)

Assuming that sin θ = 0, we can divide by sin θ to obtain

φ sin θ + 2I

θ cos θ − I



θ = 0 (4.157)

Similarly, the θ equation is

θ − I

sin θ cos θ + I



φ sin θ = mgl sin θ (4.158)

Finally, the  equation is

 = 0 (4.159)

indicating that  is constant in the previous two equations of motion.

The motion of the xyz reference frame has physical signiﬁcance. The precession rate

of the top is

φ and its nutation rate is

θ. The rotation rate of the top relative to the xyz

frame is the third Euler angle rate

ψ, given by (4.150). However, because we chose the

quasi-velocity  rather than

ψ as u

, the ﬁnal equations of motion turned out to be simpler

in form than if we had used the Lagrangian approach with

qs as velocity variables. Thus,

the ﬂexibility in the choice of us can often lead to a simpliﬁed analysis.

Example 4.6 Let us apply the general dynamical equation to the problem of the motion

of a thin uniform disk rolling on a horizontal plane (Fig. 4.2). We shall use the general form



i=1

[

· γ

+ (

+ m

) ·β

] = Q

( j = 1,...,n − m) (4.160)

Choose the reference point of the disk at its center, implying that ρ

= 0. Type II Euler

angles specify the orientation of the disk. Its angular velocity is

ω =

θe

+ ω

+ e

(4.161)

241 The general dynamical equation

where ω

φ sin θ and where e

, e

are mutually orthogonal unit vectors. Noting that

remains horizontal, we ﬁnd that the angular velocity of the unit vectors is

φ +

θ or

φ(sin θ e

+ cos θ e

) +

θe

+ ω

cot θ e

(4.162)

Assuming no slipping, the velocity of the center of mass is

v =−re

θe

(4.163)

Let the independent usbe

θ, u

= ω

, u

=  (4.164)

The γsare

∂v

∂

= r e

, γ

∂v

∂ω

= 0, γ

∂v

∂

=−re

(4.165)

From (4.161), the βsare

∂ω

∂

= e

, β

∂ω

= e

, β

∂ω

∂

= e

(4.166)

The translational momentum of the disk is

p = mv =−mre

+ mr

θe

(4.167)

Its moments of inertia are

, I

(4.168)

and the angular momentum about the center is

H =

θe

e

(4.169)

In order to ﬁnd

p and

H, we need ﬁrst to evaluate the time derivatives of the unit vectors.

= ω

× e

= ω

cot θe

− ω

= ω

× e

=−ω

cot θe

θe

(4.170)

= ω

× e

= ω

−

θe

Then we obtain

p = mr[(−

 +

θω

− (

+ ω

cot θ)e

+ (

θ + ω

]

(4.171)

H =



(

θ − ω

cot θ + 2ω

+ (˙ω

θω

cot θ − 2

θ)e

+ 2

e



(4.172)

The generalized applied forces are

=−mgr cos θ, Q

= 0, Q

= 0 (4.173)

242 Equations of motion: differential approach

Then, using (4.160), the θ equation is

θ −

cot θ +

 =−mgr cos θ (4.174)

Similarly, the ω

equation is

˙ω

θω

cot θ −

θ = 0 (4.175)

and the  equation is

 − mr

θω

= 0 (4.176)

Equations (4.174)–(4.176) are a minimum set of ﬁrst-order dynamical equations in the

us. They are identical with the equations obtained by the Boltzmann–Hamel method, but

here they are found by a much simpler procedure. Notice that the constraint equations do

not enter explicitly.

The coefﬁcients of the us in the dynamical equations are functions of θ only; and θ can be

generated by integrating u

with respect to time. So, one can obtain θ as a function of time

by integrating four ﬁrst-order equations. However, to obtain the complete conﬁguration as

a function of time, we need a total of ﬁve ﬁrst-order kinematical equations for the

qs. First,

we see from (4.162) that ω

φ sin θ or

φ =

sin θ

(4.177)

Also,

θ = u

(4.178)

and

ψ =  −

φ cos θ =−u

cot θ + u

(4.179)

Finally, the contact point C moves with a speed r

ψ having the components

x =−r

ψ cos φ = ru

cos φ cot θ − ru

cos φ (4.180)

y =−r

ψ sin φ = ru

sin φ cot θ − ru

sin φ (4.181)

These ﬁve kinematical equations plus the three dynamical equations completely determine

the motion of the disk.

For scleronomic systems such as this, the kinematical equations have the matrix form

q = Φu (4.182)

where Φ = Ψ

−1

and where Ψ is the coefﬁcient matrix in

u = Ψ

q (4.183)

For this example, we have

θ (4.184)

φ sin θ (4.185)

243 The general dynamical equation

(X, Y )

c.m.

(a)

␾

⭈

␪

(b)

⭈

Figure 4.5.

=−

φ cos θ +

ψ (4.186)

= r

ψ cos φ +

x = 0 (4.187)

= r

ψ sin φ +

y = 0 (4.188)

where the last two equations are the nonholonomic constraint equations, representing the

nonslip condition at the contact point C.

Example 4.7 As an example of a more complex nonholonomic system, consider the

motion of an unsymmetrical top with a hemispherical base, which rolls without slipping on

a horizontal plane (Fig. 4.5). Let us use the general dynamical equation in the form



i=1

(

+ ¨ρ

) ·γ

+ (I

· ˙ω

+ ω

× I

· ω

+ m

) ·β

] = Q

( j = 1,...,n − m) (4.189)

Choose the reference point O at the center of mass, implying that ρ

= 0. The xyz body

axes are principal axes at the center of mass. The orientation of the body is given by type

II Euler angles (φ,θ,ψ). These three Euler angles plus the inertial location (X, Y )ofthe

contact point on the horizontal plane constitute the ﬁve qs.

As independent us, let us choose the quasi-velocities

= ω

, u

= ω

, u

= ω

(4.190)

244 Equations of motion: differential approach

where the angular velocity of the body is

ω = ω

i + ω

j + ω

k (4.191)

The nonholonomic constraint equations, indicating no slip at the contact point, are

=−r

θ sin φ + r

ψ cos φ sin θ +

X = 0 (4.192)

= r

θ cos φ + r

ψ sin φ sin θ +

Y = 0 (4.193)

where φ is the angle between the positive X -axis and the

θ vector.

We wish to ﬁnd the velocity of the reference point O.Itis

v = ω × (r +lk) = ω × [r sin θ sin ψ i + r sin θ cos ψ j + (r cos θ + l) k]

= [(r cos θ +l) ω

−rω

sin θ cos ψ] i + [−(r cos θ +l) ω

+r ω

sin θ sin ψ] j + (rω

sin θ cos ψ − r ω

sin θ sin ψ) k (4.194)

The velocity coefﬁcients are

∂v

∂ω

=−(r cos θ + l) j +r sin θ cos ψ k

∂v

∂ω

= (r cos θ + l) i − r sin θ sin ψ k

∂v

∂ω

=−r sin θ cos ψ i + r sin θ sin ψ j

(4.195)

Similarly, the angular velocity coefﬁcients are

∂ω

= i, β

∂ω

= j, β

∂ω

= k (4.196)

We wish to ﬁnd

v and, in the process, we note that

i = ω

j − ω

j =−ω

i + ω

k = ω

i − ω

j (4.197)

The Euler angle rates are

φ = csc θ (ω

sin ψ + ω

cos ψ) (4.198)

θ = ω

cos ψ − ω

sin ψ (4.199)

ψ =−ω

cot θ sin ψ − ω

cot θ cos ψ + ω

(4.200)

Then a differentiation of (4.194) results in

v = [(r cos θ + l)˙ω

−r ˙ω

sin θ cos ψ + lω

] i

+[−(r cos θ + l)˙ω

+r ˙ω

sin θ sin ψ + lω

] j



r ˙ω

sin θ cos ψ − r ˙ω

sin θ sin ψ − l



+ ω



k (4.201)

after the cancellation of numerous terms.

245 The general dynamical equation

In the evaluation of strictly rotational terms, we ﬁnd that

· ˙ω

+ ω

× I

· ω

= [I

˙ω

+ (I

− I

)ω

] i

+[I

˙ω

+ (I

− I

) ω

] j + [I

˙ω

+ (I

− I

) ω

] k (4.202)

Furthermore, the gravitational moment about the

θ axis is

= mgl sin θ (4.203)

Hence, we obtain

= mgl sin θ cos ψ, Q

=−mgl sin θ sin ψ, Q

= 0 (4.204)

which are the generalized forces corresponding to ω

, ω

, and ω

, respectively.

Now, we are ready to ﬁnd the dynamical equations by substituting into (4.189). The ω

equation is

+mr

sin

θ cos

ψ + m(r cos θ + l)

]˙ω

− mr

˙ω

sin

θ sin ψ cos ψ

−mr(r cos θ + l)˙ω

sin θ sin ψ + [I

− I

− ml(r cos θ +l)] ω

−mrl



+ ω



sin θ cos ψ = mgl sin θ cos ψ (4.205)

Similarly, the ω

equation is

−mr

˙ω

sin

θ sin ψ cos ψ + [I

+ mr

sin

θ sin

ψ + m(r cos θ + l)

]˙ω

−mr(r cos θ + l)˙ω

sin θ cos ψ + [I

− I

+ ml(r cos θ +l)] ω

+mrl



+ ω



sin θ sin ψ =−mgl sin θ sin ψ (4.206)

The ω

equation is

−mr(r cos θ + l)˙ω

sin θ sin ψ − mr(r cos θ +l)˙ω

sin θ cos ψ

+(I

+ mr

sin

θ)˙ω

+ (I

− I

) ω

− mrlω

sin θ cos ψ

+mrlω

sin θ sin ψ = 0 (4.207)

Equations (4.205)–(4.207) are the three dynamical equations. In addition, we have three

kinematical equations for the Euler angle rates given by (4.198)–(4.200). These six equations

can be solved for (ω

,ω

,φ,θ,ψ) as functions of time. If one desires to solve for the

path of the contact point, one can write the constraint equations in the form

X = r

θ sin φ − r

ψ cos φ sin θ (4.208)

Y =−r

θ cos φ − r

ψ sin φ sin θ (4.209)

These equations are integrated to obtain X (t) and Y (t).

In this example, we have shown how the general dynamical equation can be applied using

quasi-velocities to obtain a minimum set of differential equations describing the motion of

a relatively complex nonholonomic system. This was accomplished without solving for the

constraint forces.

246 Equations of motion: differential approach

4.5 A fundamental equation

System of particles

Let us consider a system of N particles that are described by d’Alembert’s principle in the

form



i=1

− m

) ·δr

= 0 (4.210)

where r

is the inertial position vector of the ith particle, v

≡

, and F

is the applied force

acting on that particle. The δrs are consistent with any constraints.

Now suppose we express the conﬁguration of the system by using nqs with m linear

nonholonomic equations of constraint. The particle velocities are given in terms of (n − m)

independent quasi-velocities, that is,

n−m



j=1

(q, t)u

+ γ

(q, t) (4.211)

and we ﬁnd that

δr

n−m



j=1

(q, t)δθ

(4.212)

where θ

is a quasi-coordinate associated with u

. The corresponding generalized force is



i=1

· γ

( j = 1,...,n − m) (4.213)

so (4.210) takes the form

n−m



j=1



−



i=1

· γ



δθ

= 0 (4.214)

The δθs are independent, so we obtain



i=1

· γ

= Q

( j = 1,...,n − m) (4.215)

in agreement with (4.133).

Next, consider the constrained kinetic energy, written in terms of independent quasi-

velocities.

T (q, u, t) =



i=1

· v

(4.216)

247 A fundamental equation

where v

= v

(q, u, t). We ﬁnd that

∂T

∂u



i=1

∂v

∂u



i=1

· γ

( j = 1,...,n − m) (4.217)

Then



∂T

∂u





i=1

(

· γ

+ v

· ˙γ

) (4.218)



i=1

· γ



∂T

∂u



−



i=1

· ˙γ

( j = 1,...,n − m) (4.219)

Finally, from (4.215) and (4.219) we obtain



∂T

∂u



−



i=1

· ˙γ

= Q

( j = 1,...,n − m) (4.220)

This is a fundamental dynamical equation for a system of particles. It results in (n − m)

ﬁrst-order dynamical equations which are supplemented by the n ﬁrst-order kinematical

equations for the

qs. These (2n − m) equations are solved for the (n − m) us and nqsas

functions of time.

Notice that the dynamical equations are identical to those obtained by the Boltzmann–

Hamel equation but the procedure here is far simpler. Furthermore, the kinetic energy

T (q, u, t) is written for the constrained rather than the unconstrained system.

System of rigid bodies

Let us generalize the results for a system of N particles to a system of N rigid bodies. Let

us choose the reference point for each rigid body at the center of mass. Then in accordance

with Koenig’s theorem, the kinetic energy is

T (q, u, t) =



i=1

· v

+ ω

· I

· ω

) (4.221)

where v

is the velocity of the center of mass of the ith body and I

is its inertia dyadic

about the center of mass. The (n − m) us are independent.

We see that

∂T

∂u



i=1

· γ

+ ω

· I

· β

)(j = 1,...,n − m) (4.222)

where

∂v

∂u

, β

∂ω

∂u

(4.223)

248 Equations of motion: differential approach

Hence, we obtain



∂T

∂u





i=1

· γ

+ (I

· ˙ω

+ ω

× I

· ω

) ·β

]



i=1

· ˙γ

+ ω

· I

)(j = 1,...,n − m) (4.224)

Now recall the general dynamical equation for center-of-mass reference points, that is, for

= 0. From (4.142), we have



i=1

· γ

+ (I

· ˙ω

+ ω

× I

· ω

) ·β

] = Q

( j = 1,...,n − m) (4.225)

Finally, from (4.224) and (4.225), we obtain



∂T

∂u



−



i=1

· ˙γ

+ ω

· I

) = Q

( j = 1,...,n − m) (4.226)

This is a fundamental equation for a system of rigid bodies. Using the kinetic energy

T (q, u, t)fortheconstrained system, it results in a minimum set of (n − m) ﬁrst-order

dynamical equations.

An alternate form of (4.226) is



∂T

∂u



−



i=1

· ˙γ

+ H

) = Q

( j = 1,...,n − m) (4.227)

where p

is the linear momentum of the i th body and H

is its angular momentum about

its center of mass. This form of the equation is more ﬂexible in that the angular momentum

may be expressed in terms of arbitrary unit vectors rather than being tied to the body-ﬁxed

unit vectors of the inertia dyadic. This is particularly useful in the dynamic analysis of

axially symmetric bodies.

If we compare (4.227) with the Boltzmann–Hamel equation, as given by (4.82), we ﬁnd

that



i=1

· ˙γ

+ H

) =



i=1

∂T

∂q



−



i=1



j=1



k=1

n−m



l=1

∂T

∂u



∂

∂q

−

∂

∂q





−



i=1



j=1



k=1

∂T

∂u



∂

∂q

−

∂

∂q





−



i=1



j=1

∂T

∂u



∂

∂t

−

∂

∂q





(r = 1,...,n − m) (4.228)

where T (q, u, t) is written for the unconstrained system. Since the differential equations

of motion produced by the two methods are identical, we conclude that the fundamental