Greenwood D.T. Advanced Dynamics

Подождите немного. Документ загружается.

279 Problems

4.10 Problems

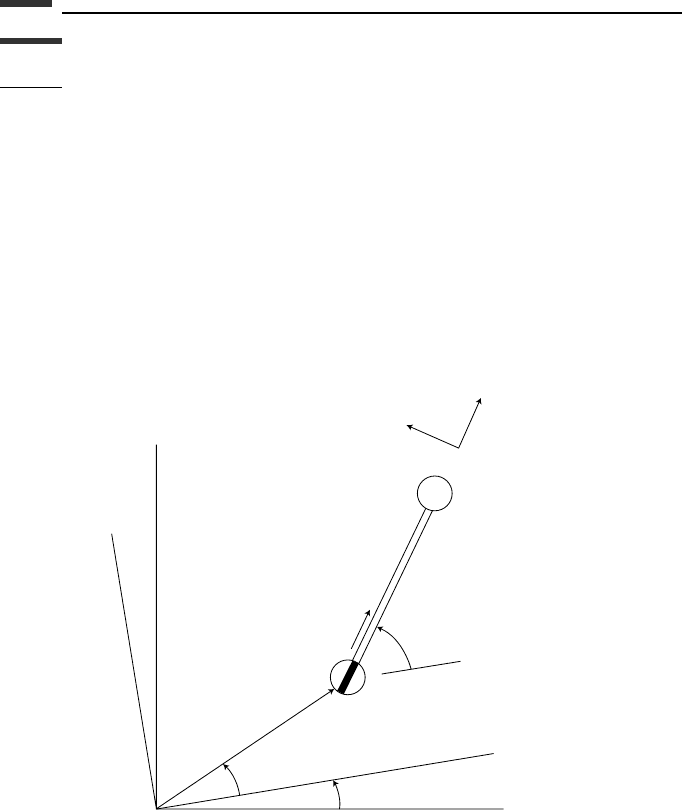
4.1. Suppose we wish to analyze the unsymmetrical top of Example 4.7, using Maggi’s

equation. Referring to Fig. 4.5 on page 243, let the generalized coordinates be

(φ,θ,ψ, X, Y ) where φ is the angle between the positive X-axis and the

θ vector.

Let the independent usbeu

φ, u

θ, and u

ψ. (a) Obtain the unconstrained

kinetic energy T (q,

q) and the potential energy V (q). (b) Write the constraint equa-

tions. (c) Find Q

and 

for i = 1,...,5 and j = 1, 2, 3.

4.2. Two particles, each of mass m, are connected by a massless rod of length l. They can

move on a horizontal turntable which rotates at a constant rate . There is a knife-edge

constraint at particle 1 which allows no velocity relative to the turntable in a direction

normal to the knife edge. Use (r,θ,φ)asqs and (v

φ) as independent us, where v

is the speed of particle 1 relative to the turntable. (a) Find the differential equations of

motion. (b) Evaluate the energy rate

Ω

Figure P 4.2.

4.3. A sphere of mass m, radius r, and central moment of inertia I rolls without slipping in

a ﬁxed horizontal cylinder (Fig. P 4.3). Choose (ω

,ω

) as quasi-velocities, where

ω is the angular velocity of the sphere. Use the Gibbs–Appell equation to obtain the

differential equations of motion.

280 Equations of motion: differential approach

Figure P 4.3.

4.4. A sphere of radius r,massm, and central moment of inertia I can roll without slipping

on a wedge of mass m

and wedge angle α. The XY Z frame is inertial with the Z -axis

vertical. The xyz frame is ﬁxed in the wedge; the xy-plane forms the slanted surface

on which the contact point C moves. The wedge can slide on the horizontal XY-plane

without friction, but in the Y -direction only. Its speed in this direction is v. There is

no rotation of the wedge. (a) Use the general dynamical equation or the Gibbs–Appell

equation to ﬁnd the differential equations of motion. Let the sphere be body 1 with the

reference point at its center. The wedge is body 2. Choose (ω

,ω

,v)asus, where

ω is the angular velocity of the sphere. (b) If the contact point C is located at (x, y)

relative to the wedge, write the kinematic equations for

x and

wedge

sphere

x, X

(x,y)

Figure P 4.4.

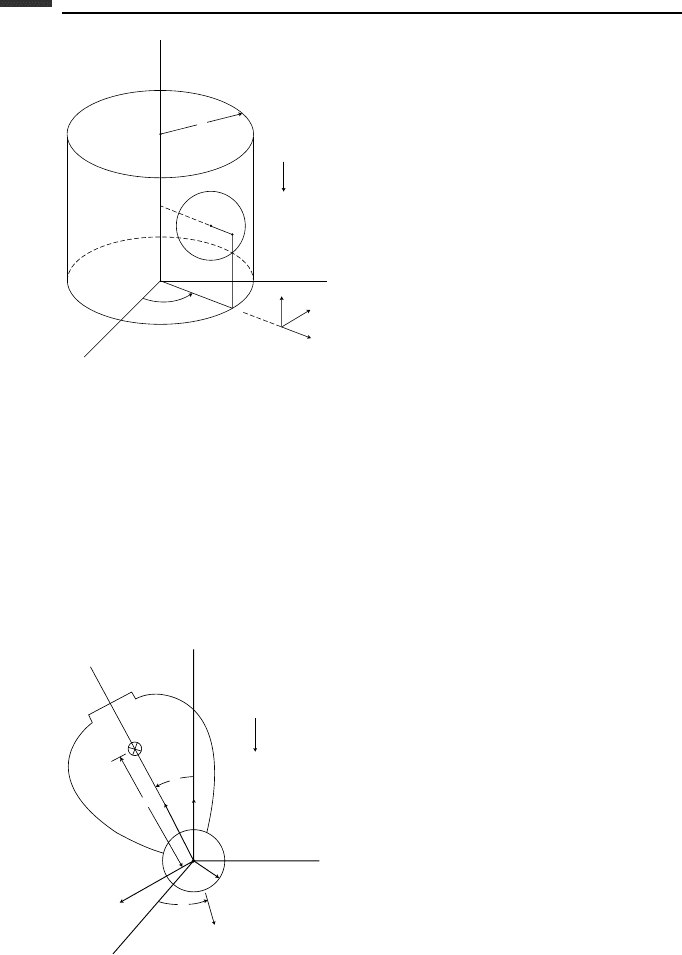
4.5. Consider a sphere of mass m, radius r , and central moment of inertia I which rolls

without slipping on the inside surface of a ﬁxed vertical cylinder of radius R (Fig. P4.5).

(a) Choose the angular velocity components (ω

,ω

) as quasi-velocities and obtain

the differential equations of motion. (b) Show that the vertical motion of the sphere is

sinusoidal.

281 Problems

sphere

Figure P 4.5.

4.6. An axially-symmetric top with a spherical point moves without slipping on a horizontal

plane. The xy-plane remains horizontal and there is no rotation of the xyz frame about

its vertical z-axis. Classical Euler angles (φ,θ,ψ) are used to specify the orientation of

the top. The orthogonal e

unit vector triad has e

along the symmetry axis and e

remains horizontal. The center of mass C is located at a distance l from P, the center of

the spherical point. The top has mass m and moments of inertia I

about the symmetry

axis and I

about a transverse axis through P. Choose angular velocity components

(ω

,ω

) of the top as quasi-velocities and obtain the differential equations of

motion by using the general dynamical equation.

q,e

␾

Figure P 4.6.

282 Equations of motion: differential approach

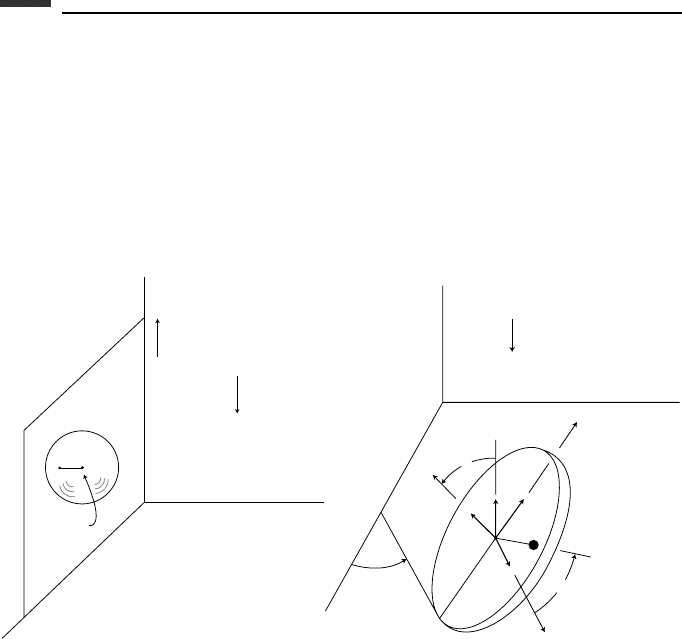
4.7. A uniform sphere of radius r ,massm, and central moment of inertia I rolls without

slipping on the vertical xz-plane which rotates about the ﬁxed z-axis at a constant

rate >0. The sphere has a center C at (x, y, z) and P is the contact point. Choose

the components (ω

,ω

) of the angular velocity ω of the sphere as independent

quasi-velocities. (a) Find the differential equations of motion by using the fundamental

dynamical equation. (b) Assume the initial conditions x(0) = x

> 0,

x(0) = v

> 0,

y(0) = r ,

y(0) = 0, z(0) = z

z(0) = 0, ω

(0) = 0. Show that the vertical velocity

is a sinusoidal function of time. (c) What is the minimum value of v

that will ensure

that the sphere will remain in contact with the xz-plane?

Ω

(x, y, z)

sphere

␪

␾

␻

⍀

Figure P 4.7. Figure P 4.8.

4.8. A thin uniform disk of mass m and radius r rolls without slipping on the horizontal

xy-plane. A particle of mass m

is attached at a distance l from its center. Choose the

classical Euler angles (φ,θ,ψ)asqs and let the usbe(

θ,ω

,). Consider the disk

and particle as separate bodies and take the reference point of the disk at its center.

Use the general dynamical equation to obtain the equations of motion.

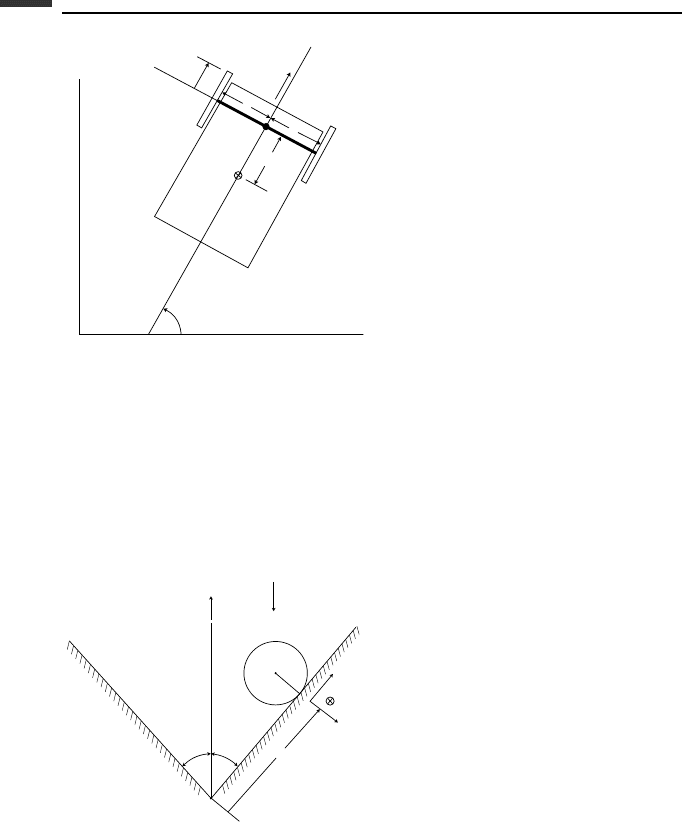
4.9. A two-wheeled cart consists of body 1 of mass m

and moment of inertia I

about its

center of mass C , plus wheels 2 and 3, each a thin uniform disk of mass m and radius r .

The wheels roll without slipping, and the body slides without friction on the horizontal

XY-plane. The center of mass C of the body is at a distance l from P, where P is the

midpoint of the rigidly attached axle of length 2b. Obtain the differential equations of

motion using (v,

θ) as quasi-velocities, where v is the speed of P in the direction of

the x -axis.

283 Problems

Figure P 4.9.

4.10. A uniform sphere of mass m, radius r, and central moment of inertia I rolls without

slipping on the inside surface of a cone that has a vertical axis and a vertex angle

α. Let

φ be the angular velocity of the center C about the vertical axis, and let ω

be the angular velocity of the sphere. Use the components (ω

,ω

)asquasi-

velocities and obtain the differential equations of motion. To simplify the algebra,

use the notation b ≡ r/(R sin α − r cos α) which is ratio of r to the distance of the

center C from the vertical axis.

␾

Figure P 4.10.

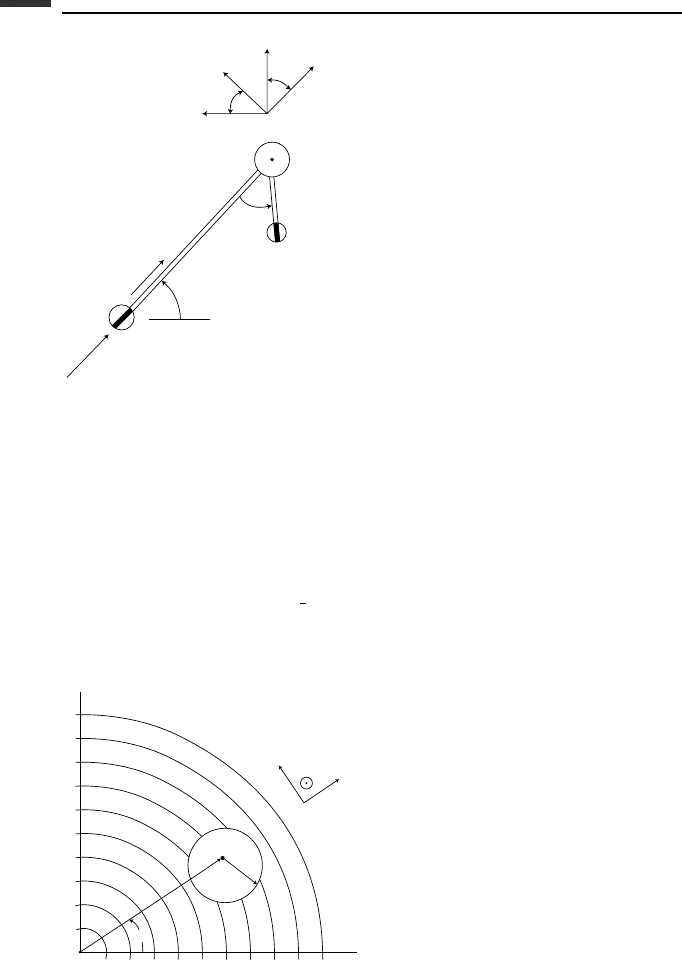
4.11. The system of three particles (Fig. P 4.11) approximates the dynamical characteristics

of a cart with castered wheels. Particle 1 with its knife edge represents the rear wheels.

Particle 3 with its knife edge represents the front wheels that have an offset l. There is

a joint at particle 2. The force F is constant in magnitude and is directed longitudinally

along e

.Use(v,

θ) as quasi-velocities and obtain the differential equations of motion.

284 Equations of motion: differential approach

Figure P 4.11.

4.12. A sphere of mass m, radius r , and central moment of inertia I rolls on the horizontal

xy-plane which has a system of concentric knife edges embedded in it. At the contact

point (R,θ) between the sphere and the horizontal plane, there is no slipping in the

radial direction, but slipping can occur without friction in the e

direction. (a) Obtain

the differential equations of motion using (v

,ω

) as quasi-velocities, where

v is the velocity of the center of the sphere and ω is its angular velocity. (b) Find

the angular momentum about the origin O and show that it is conserved. (c) Assume

that m = 1, r = 1, and I =

in a consistent set of units. If the initial conditions are

R(0) = 10, θ(0) = 0, v

(0) = 1 and ω(0) = 0, solve for the ﬁnal values of θ, v

, ω

and ω

Figure P 4.12.

285 Problems

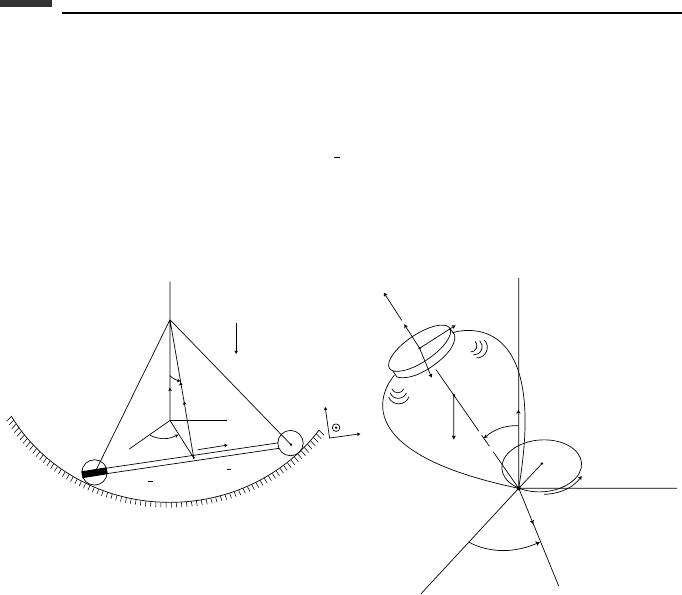
4.13. A dumbbell consists of two particles, each of mass m, connected by a massless rod of

length l. It moves on a smooth spherical depression of radius r. The conﬁguration of

the system is given by the generalized coordinates (α, θ, φ), where θ>0 and where

the positive

φ vector is in the e

direction. Let φ = 0 when the rod is horizontal. The

unit vectors e

and e

lie in the plane of triangle O12. The center of mass C moves

on a sphere of radius R = (r

−

)

1/2

. A knife-edge constraint allows no velocity

component of particle 1 in the e

direction. Choose (v, ω

) as independent us, where

v is the velocity component of C in the e

direction and ω

is the e

component of the

angular velocity ω of O12. (a) Find the differential equations of motion. (b) Obtain

the kinematic expressions for ˙α,

θ, and

φ as functions of the qs and us.

␻

␣

␾

Ω

Figure P 4.13. Figure P 4.14.

4.14. The point P of an axially symmetric top moves with a constant angular velocity ω

around a horizontal circular path of radius r .Attimet = 0, the line OP has the

direction of the positive X -axis. The frame XY Z is nonrotating and translates with

P. Use type II Euler angles as qs and (

φ,

θ,)asus, where  is the total angular

velocity about the symmetry axis. (a) Find the differential equations of motion. (b)

Obtain the energy rate

E as a function of (q, u, t), assuming that the kinetic energy

is calculated relative to the XYZ frame. (c) Find the possible steady precession

rates, that is,

φ = ω

with the top leaning outward at a constant angle θ

and with

φ − ω

t = π/2. Assume that 

is sufﬁciently large to ensure stability.

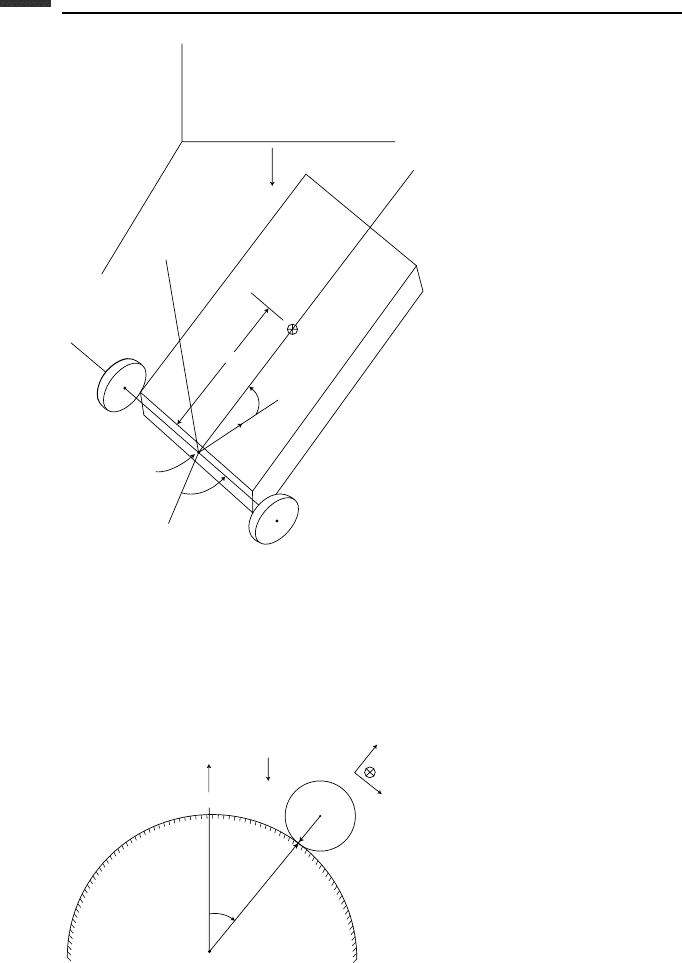
4.15. A rectangular block of mass m has a massless axle and wheels attached along its base,

and can roll without slipping on the horizontal XY-plane (Fig. P 4.15). The origin O

of the xyz body-ﬁxed principal axis system is the reference point at the midpoint of

the axle. The y-axis is horizontal and the x-axis makes an angle θ with the horizontal

plane. Choose (X, Y,φ,θ) as generalized coordinates and (v,

φ,

θ)asus. (a) Obtain

the differential equations of motion. (b) Find the kinematic equations for

X and

Y .

286 Equations of motion: differential approach

(X,Y )

c.m.

Figure P 4.15.

4.16. A uniform sphere of mass m, radius r, and central moment of inertia I rolls without

slipping on a ﬁxed sphere of radius R. Let the coordinates (φ,θ) specify the location

of the center C and choose (ω

,ω

) as quasi-velocities, where ω is the angular

velocity of the sphere. (a) Obtain the differential equations of motion. (b) Show that

the motion of the line OC is similar to that of the symmetry axis of a top with a ﬁxed

point.

Figure P 4.16.

287 Problems

4.17. A particle of mass m moves relative to a ﬁxed Cartesian xyz frame under the action

of a constant force F

that is directed parallel to the positive x-axis. There is a

nonholonomic constraint of the form

z − k



= 0

where k is a positive constant. Note that k = tan β where β is the constant angle of the

velocity vector v above the horizontal xy-plane. Let (x, y, z) denote the position of

the particle and choose (v, φ)asus, where v = (

)

1/2

and tan φ =

Obtain the differential equations of motion.

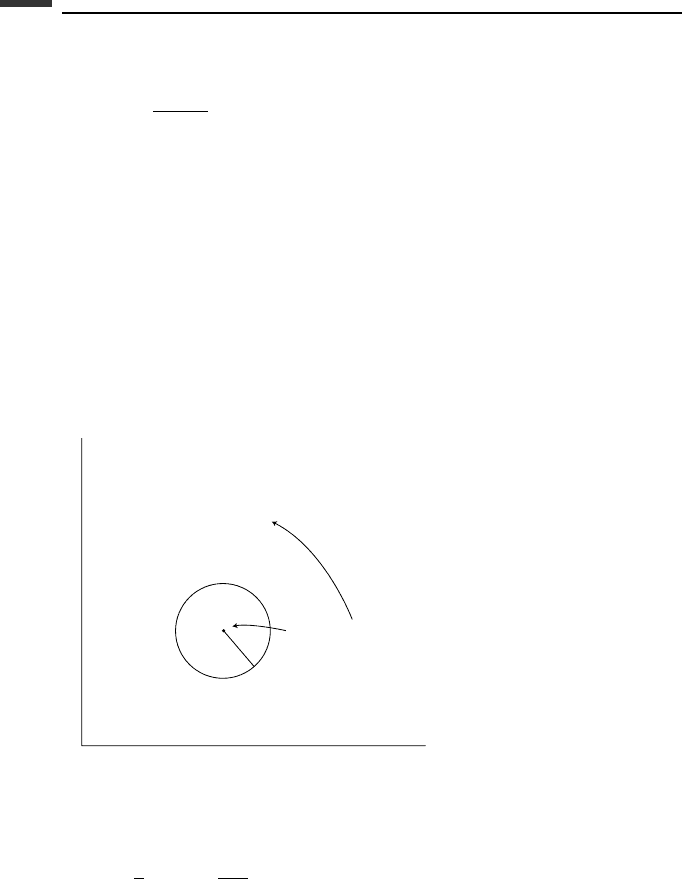
4.18. A uniform sphere of mass m, radius r, and central moment of inertia I rolls without

slipping on a horizontal turntable which rotates at a constant rate  about its center

O. The xyz frame is inertial and the coordinates of the center C of the sphere are

(x , y, r). Let ω be the angular velocity of the sphere and choose (ω

,ω

)as

quasi-velocities. (a) Obtain the differential equations of motion. (b) Assuming general

initial conditions x(0) = x

, y(0) = y

x(0) =

y(0) =

, show that the path of

C is circular by solving for x(t) and y(t ). (c) Show that the horizontal component of

the angular momentum about O is constant.

(x, y)

Ω

Figure P 4.18.

4.19. A uniform sphere of mass m, radius r, and central moment of inertia I rolls without

slipping on a ﬁxed wavy surface described by

z =



1 −cos

2π y



where h/L << 1 (Fig. P 4.19). (a) Choose the angular velocity components

(ω

,ω

) of the sphere as quasi-velocities and use the general dynamical equation

to obtain the differential equations of motion. Retain terms to ﬁrst order in the small

parameter h/L. (b) Give the kinematic differential equation for

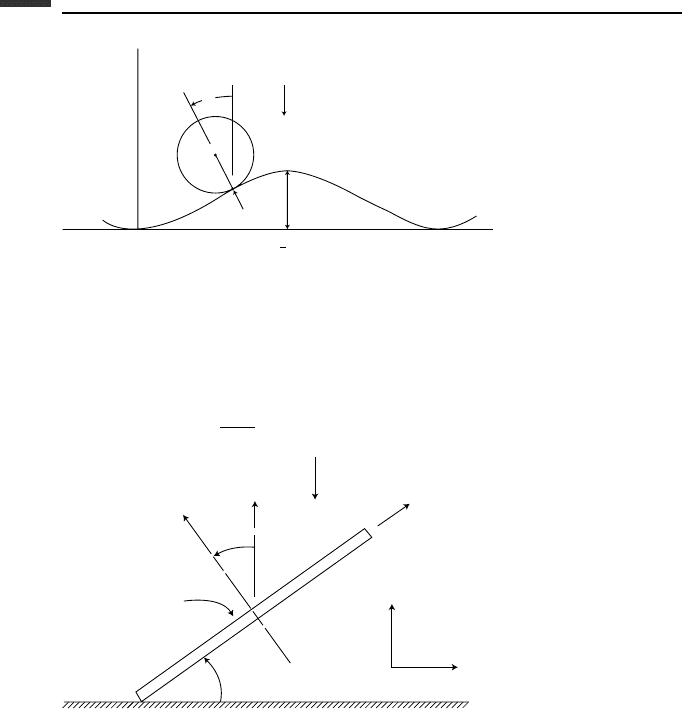
288 Equations of motion: differential approach

(x, y, z)

Figure P 4.19.

4.20. A thin uniform disk of mass m and radius r moves on a frictionless horizontal plane.

Choose type II Euler angles (φ, θ,ψ) as generalized coordinates. The usare(

θ,ω

,)

where  is the total angular velocity about the symmetry axis and ω

is the angular

velocity about a diameter through the contact point. (a) Obtain the differential equa-

tions of motion. (b) Consider the case of motion with small positive θ, positive ω

and let  =−

√

2g/r. Solve for ω

and the precession rate

φ.

Ω,ψ

disk

Figure P 4.20.