Грачева М.В. и др. Моделирование экономических процессов

Подождите немного. Документ загружается.

ливо и для графика прибыли PR(jc

,jc

) при х\ >

и х

0. Для того

чтобы функция -PR(x

) (или функция -f(x

)) была выпукла

вниз,

необходимо и достаточно, чтобы все главные миноры матрицы

f(x

) d

f(x

)

dxt

дх\дх

д f(x

) д f(x

)

дх

дх\

т.е.

миноры

f(x

)

дх

д f(x

)

dx?

д f(x

)d f(x

)

дх

f(x

{

)

дх

построенные на элементах, расположенных на пересечении строк и

столбцов этой матрицы с одинаковыми номерами, были неотрица-

тельными при всех х\ > 0 и х

> 0.

Если последовательно повышающие порядок угловые миноры

вышеприведенной матрицы строго положительны, т.е. при всех х\ > 0,

> 0 справедливы неравенства:

f(x

) _ d

f(x

) d

f(x

)

(.&

dxt

<0,

dxt

dxl

f(x

)

dxidx?

>o,

то производственная функция y

f(x

) есть функция (строго)

выпуклая вверх, график производственной функции у ~А

трехмерном пространстве Ojqjx^ есть поверхность (строго) выпук-

лая вверх. График прибыли PR(JCI, Х

)

получаемый путем вычита-

ния из графика функции /?о/(*ь

т) плоскости у = р\Х\ +

(ко-

торая является графиком издержек), имеет вид «шапочки», у кото-

рой есть «макушка». Макушка соответствует глобальному максиму-

му прибыли:

PR(x

) = pof(x

) - (р\х

{

Для строго выпуклой вверх производственной функции у = f(x

)

система (4.1) имеет единственное решение (х® , х

)

которое являет-

ся тонкой не только локального, но и глобального (искомого нами)

максимума прибыли PR(jq, х

). Вектор (х,°, х

) затрат ресурсов,

который является решением задачи глобальной максимизации при-

были PR(x

) = РоА

2) "" (Р\Х\ + P2

i)> называется локальным

(частичным) рыночным равновесием фирмы (в случае долговременно-

110

го промежутка). Термин «локальный применительно к рыночному

равновесию» здесь используется в связи с тем, что рассматривается

единственная фирма, функционирующая на рынках ресурсов и на

рынке готовой продукции.

График прибыли PR(X|, х

) в трехмерном пространстве, вообще

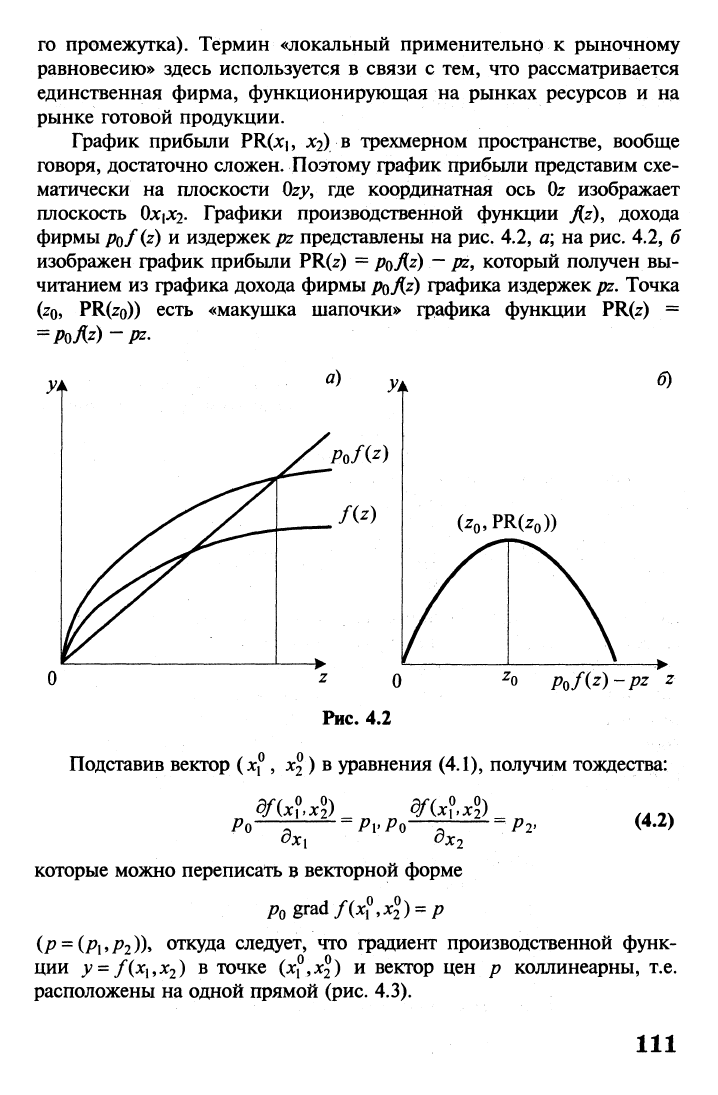
говоря, достаточно сложен. Поэтому график прибыли представим схе-

матически на плоскости Ozy, где координатная ось Oz изображает

плоскость 0JC|JC2- Графики производственной функции fiz), дохода

фирмы Pof(z) и издержек pz представлены на рис. 4.2, а; на рис. 4.2, б

изображен график прибыли PR(z) =

РоЛ

)

Р*,

который получен вы-

читанием из графика дохода фирмы

p^fiz)

графика издержек

pz.

Точка

PR(zo))

есть

«макушка шапочки» графика функции PR(z) =

PoAz)-pz.

б)

Pof(

)~P

z z

Рис. 4.2

Подставив вектор (xf, х

) в уравнения (4.1), получим тождества:

Ро

dfixUl)

PvPo

dfixUi)

(4.2)

дх

5JC

которые можно переписать в векторной форме

gmdf(xi,x%)~p

= (Pi>p

))>

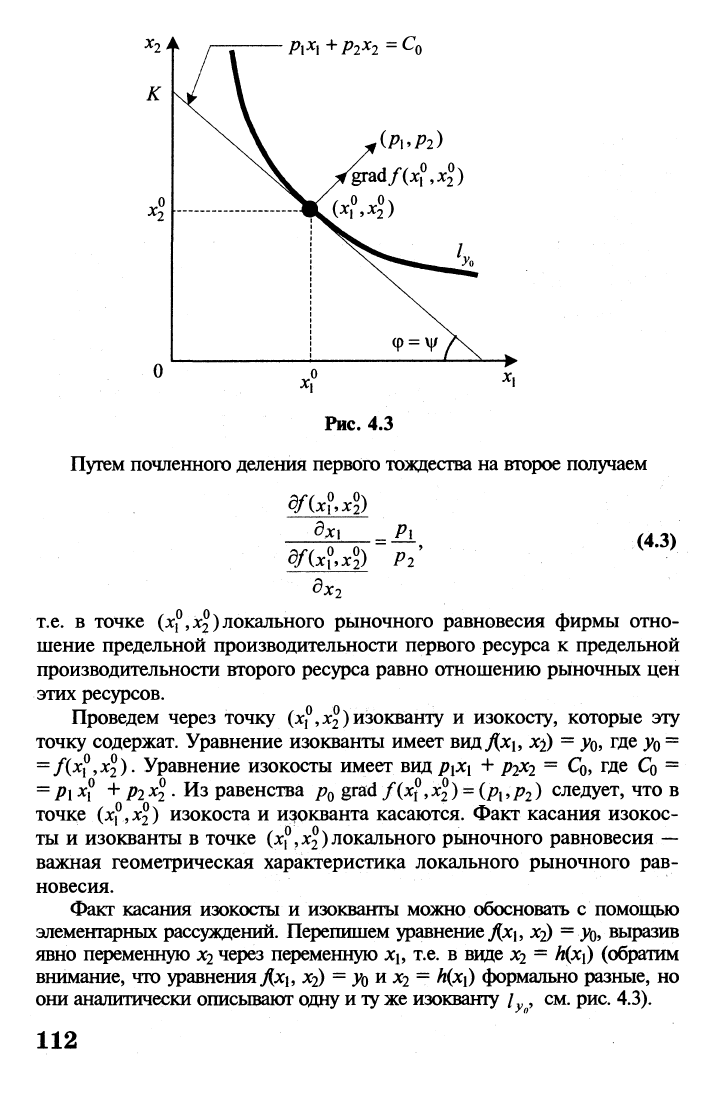
откуда следует, что градиент производственной функ-

ции y

f(x

) в точке (xi

x$) и вектор цен р коллинеарны, т.е.

расположены на одной прямой (рис. 4.3).

111

А г—

= С

х°

1 (Xj , Х

)

х>-Л

¥/\

Рис.

4.3

Путем почленного деления первого тождества на второе получаем

дх\

Р\

dfixUD Pi

(4.3)

т.е.

в точке (х

,х

)локального рыночного равновесия фирмы отно-

шение предельной производительности первого ресурса к предельной

производительности второго ресурса равно отношению рыночных цен

этих ресурсов.

Проведем через точку (х^х^изокванту и изокосту, которые эту

точку содержат. Уравнение изокванты имеет вид/хь х^) =

уо,

где у

/(х

,х

Уравнение изокосты имеет вид

р\Х\

= Q, где Q =

= р\ xf + р

х\

Из равенства р

grad f(x^,x

)

{р

,р

) следует, что в

точке (х

,х

) изокоста и изокванта касаются. Факт касания изокос-

ты и изокванты в точке (х

Х}

)локального рыночного равновесия

—

важная геометрическая характеристика локального рыночного рав-

новесия.

Факт касания изокосты и изокванты можно обосновать с помощью

элементарных рассуждений. Перепишем уравнение/xj, х

) =

уо,

выразив

явно переменную х

через переменную х\, т.е. в виде х

— h(x{)

(обратим

внимание, что уравнения Дхь х

) =

Уо

и х

h(x{)

формально разные, но

они аналитически описывают одну и

ту же

изокванту /

Уд

, см. рис. 4.3).

112

Из математического анализа известно, что

„-*£-

{

а»

дх

(4.4)

Для изокосты

р\Х\

/>2*2

Q имеем отношение —

tgy. Из ра-

Рг

венств (4.3) и (4.4) следует, что

tgq>

= tg\|/, что означает, что касательная

К к изокванте / в точке (х

Х9

) совпадает с изокостой, т.е. в точке

(х®

) изокванта /^обязательно касается изокосты А'(см. рис. 4.3).

Отметим, что, приступая к решению задачи максимизации при-

были, мы не имели конкретных изокванты и изокосты, которые ка-

саются друг друга в точке

(х

Х9

)

ибо не имели самой этой точки.

Касающиеся друг друга изокванта и изокоста появляются после того,

как аналитически найдено локальное рыночное равновесие (xf,

JC^

)

путем решения системы уравнений (4.1).

Левая («четырехэтажная») дробь в (4.3) есть не что иное, как

Rn(xi,x

) — предельная норма замены первого ресурса вторым в

точке

(х

Х9

Равенство (4.3) выражает следующий фундаментальный факт тео-

рии фирмы: в точке локального рыночного равновесия (х

,х

) пре-

дельная норма замены

Я\2(х?

)

пе

В0Г0

ресурса вторым равна отно-

Р\

шению —

рыночных цен этих ресурсов.

Поскольку Xi и х

получаются в виде решения системы уравне-

ний (4.1), постольку

х®

и х

есть функции цен

(ро,

р\

pi), т.е.

*л =d

)\ х

). (4.5)

Выражения (4.5) называются

функциями спроса

на

ресурсы

{затра-

ты) со стороны фирмы на рынках ресурсов. Их значения х® и х

выражают оптимальный выбор ресурсов как функции цены выпус-

каемой продукции и цен на ресурсы.

Подставив функции (4.5) в производственную функцию у=/(х\

л^),

получим выражение:

У*

f{dx(Po,PuP

))

s(p

)

которое называется

функцией предложения выпуска

фирмы на рынке.

113

Функции спроса на ресурсы и функция предложения выпуска яв-

ляются однородными нулевой степени по всем своим аргументам ро,

Рх

Р2,

т.е.

di(ypo,

урь

УР2)

diipo,

pi);

(ypo,

ур

УР2)

pi);

s(yPo> УРь

У Pi)

= s

(Аь

PI) дая любого числа у > 0. Свойство одно-

родности означает, что одновременное изменение всех цен ро,Ри Pi

одно и то же число раз у (т.е. при изменении масштаба, но не струк-

туры цен) не меняет jq

, x

° и/, что важно с содержательной точки

зрения. С математической точки зрения однородность нулевой степе-

ни функции спроса и функции предложения является простым фак-

том, ибо максимизация прибыли PR(x

) = уРоА*ь х

)

(УР\Х\

уР2Х

)

сводится к системе уравнений (4.2), ибо на множитель у > 0

можно сократить.

Вернемся к задаче глобальной максимизации прибыли фирмы:

РоЛхи х

) -

Р\х\

= PR(x

) => max.

Вполне возможно, что фирма имеет определенный лимит К на при-

обретение ресурсов, т.е. фирма может приобретать ресурсы, количе-

ства которых х\ и х

должны удовлетворять ограничению:

P\Xi+p

В этом случае задача глобальной максимизации прибыли приобретает вид:

/>о/(*ь х

) - V = PR -* max,

что эквивалентно глобальной максимизации выпуска Л

\, х

)

И на

личии лимита на ресурсы

р\Х\

= V.

Таким образом, получаем задачу глобальной максимизации вы-

пуска фирмы при наличии лимита на ресурсы:

fix\,

)

з=> max;

Р\х\

= V.

Выписанная задача (она анализируется в параграфе 4.4) пред-

ставляет собой частный случай известной задачи рационального

распределения ограниченных ресурсов.

Рассмотрим еще одну корректировку задачи глобальной макси-

мизации прибыли фирмы.

Если фирма получает фиксированный заказ на свою продукцию

в объеме у (у = J{x\, x

))

который фирма должна выполнить в те-

чение временного периода, то задача глобальной максимизации

прибыли фирмы приобретает вид:

Роу -Р\х\ - Pix

=PR =>• max,

что эквивалентно глобальной минимизации издержек фирмы

С(х\,

) =

Р\Х\

при наличии фиксированного заказа в объеме у еди-

ниц выпускаемой фирмой продукции.

114

Таким образом, получаем задачу глобальной минимизации из-

держек фирмы при фиксированном объеме выпускаемой ею про-

дукции:

Р\Х\ +

Р2*2

С-> min,

у =/(х

Вьшисанная задача анализируется в параграфе 4.5.

В случае, когда число факторов п

2, условия первого порядка

(4.1) имеют следующий вид:

д/(х) д/(х)

Ро~т—

Л>->А)-Т—

Рп>

(х

...

дх

{

дх

Как и в случае п = 2 выпуклость вверх функции fix\, ...,

JCn)

экви-

валента выпуклости вниз функции

-Д*1,

..., х

Для того, чтобы функция -f(x

...

) была выпукла вниз (а

функция f(x

...

) выпукла вверх), необходимо и достаточно, что-

бы все главные миноры матрицы Гессе функции -f(x

...

)

/(х)

дх}

f(x)

дх

Дх)

дх

Дх)

дх

X — ^Xj

...

)

т.е.

миноры, построенные на элементах, расположенных на пересе-

чении строк и столбцов этой матрицы с одинаковыми номерами,

были неотрицательными при всех х\

О, ...,

x-i

Если последовательно повышающие порядок угловые миноры

вышеприведенной матрицы Гессе строго положительны, т.е. при всех

Х[ > 0, ..., Х

> 0

f(x

)

дх?

>0,

Ях)

дх

f(x)

dxi

f{x)\

дх^дх

Дх)

дх\

>0,.

Ах)

дх

f(x)

дх„дх

Дх)

дх

{

дх„

/(х)

dxi

>0,

производственная функция f(x)

f(x

...,x„) строго выпукла

вверх.

115

Для строго выпуклой вверх производственной функции

f(x

...,x

) условиям первого порядка удовлетворяет единствен-

ная точка х° =(х,°,...,х^) глобального (искомого) максимума при-

были PR(jt,,...,x

Как и при

= 2, точка (вектор)

JC°

=(лг

°,...,х^) называется ло-

кальным

рыночным

равновесием фирмы (в случае долговременного

промежутка).

Подставив точку х° =(X

,...,JC^) в условия первого порядка, полу-

чим равенства:

df(x°)_

df(x°) _

откуда следует, что

grad Дх°) = р (р

(р

...,р

)),

т.е.

градиент производственной функции у = f(x

,...,x

) в точке локаль-

ного рыночного равновесия х° = (xf, ...,х^) и вектор цен р

..., р

)

коллинеарны, а это означает, что в пространстве ресурсов поверх-

ность постоянного вьшуска у° = f(x°)

(т.е.

изокванта) и (п

—

1)-мерная

плоскость постоянных издержек (т.е. изокоста), содержащие точку

х°

(х,°,...,

х%),

касаются.

4.3.

Функции спроса на факторы (ресурсы)

в случае краткосрочного промежутка

В случае

краткосрочного

промежутка (s

) рассмотрим конкрет-

ный пример, когда первый ресурс (капитал) фирма может исполь-

зовать только в объеме, равном х

{

> 0. Тогда задача максимиза-

ции прибыли превращается в задачу максимизации функции од-

ной переменной

PR(х

{

,х

)

/(*,,

)

(р

[

и вместо системы уравнений (4.1) появляется только одно урав-

нение

d?R(x

)

df(x

) ,. ..

i-^-li

= 0, или

Ро

yv 1? 2/

= р

. (4.6)

ОХ

116

Как и в параграфе 4.2, считаем (исходя из содержательных эко-

номических соображений), что уравнение (4.6) имеет единственное

решение х

—

(х

зависит от х

, т.е. х

= x

(*i

))>

следовательно,

в случае краткосрочного промежутка локальное рыночное равнове-

сие есть вектор (х

{

, Зс

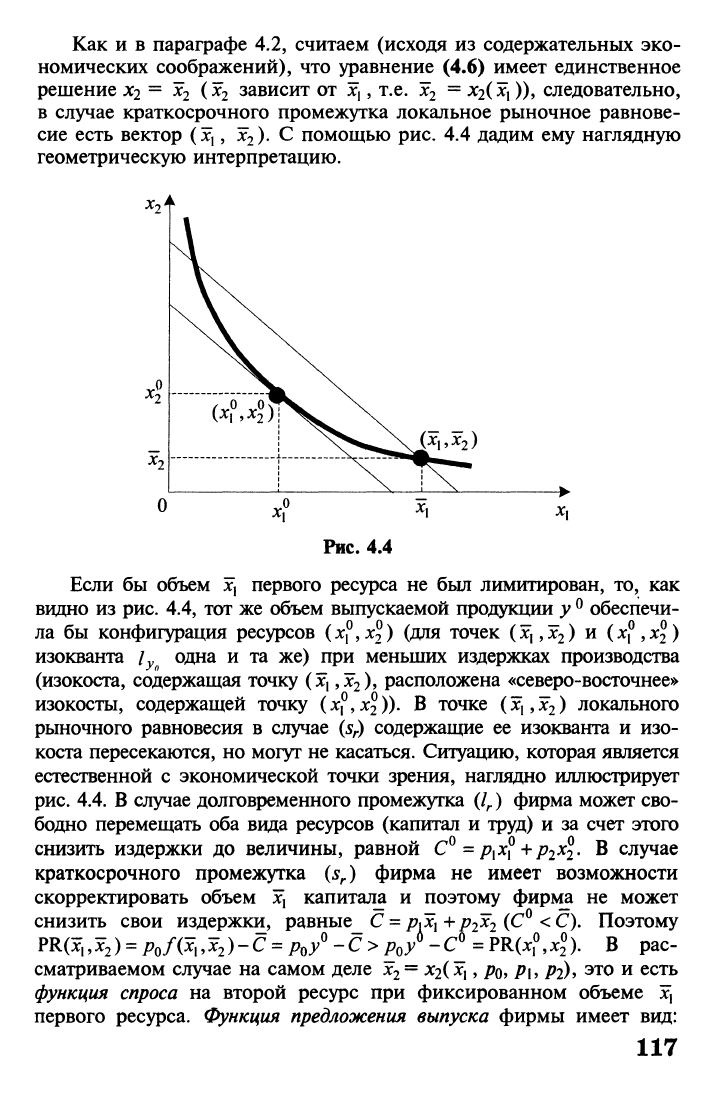
). С помощью рис. 4.4 дадим ему наглядную

геометрическую интерпретацию.

Рис. 4.4

Если бы объем Зс, первого ресурса не был лимитирован, то, как

видно из рис. 4.4, тот же объем выпускаемой продукции у

обеспечи-

ла бы конфигурация ресурсов (х®,х

) (для точек (х

) и (х? ,х

)

изокванта 1

одна и та же) при меньших издержках производства

(изокоста, содержащая точку (3tj ,3с

), расположена «северо-восточнее»

изокосты, содержащей точку (х®,х

)). В точке (Зс,,3с

) локального

рыночного равновесия в случае (s

) содержащие ее изокванта и изо-

коста пересекаются, но могут не касаться. Ситуацию, которая является

естественной с экономической точки зрения, наглядно иллюстрирует

рис.

4.4. В случае долговременного промежутка (/

) фирма может сво-

бодно перемещать оба вида ресурсов (капитал и труд) и за счет этого

снизить издержки до величины, равной С

= Р[Х°

+р

х%.

В случае

краткосрочного промежутка (s

) фирма не имеет возможности

скорректировать объем х

капитала и поэтому фирма не может

снизить свои издержки, равные_ С =

р,

Зс,

(С

С).

Поэтому

РК(х

) =

/(х

)-С = /?

/-С>^

/--С^==РК(л:

,х

). В рас-

сматриваемом случае на самом деле х

(х

{

/>о,

Р\, />

эт

о и есть

функция спроса на второй ресурс при фиксированном объеме Зс,

первого ресурса. Функция

предложения

выпуска фирмы имеет вид:

117

f(x

)). Может случиться так, что точки (х

{

,х

) и

(х,°,Х2) сольются в одну, и тогда получится та ситуация, которая

уже была проанализирована в параграфе 4.2.

4.4.

Комбинация ресурсов (факторов

производства), максимизирующая объем

выпуска при ограничении на затраты

Для случая

долговременного

промежутка

)

сначала рассмотрим за-

дачу глобальной максимизации объема вьшускаемой продукции при

наличии лимита на ресурсы (при ограничении затрат на приобретение

ресурсов (факторов)) в следующем виде:

f(x\,

X2>->

max (4.7)

при условии, что

Р\х\

Р2*2

£ V, (4.8)

0, х

0. (4.9)

Величина Кне обязательно равна величине Q (см. параграф 4.2).

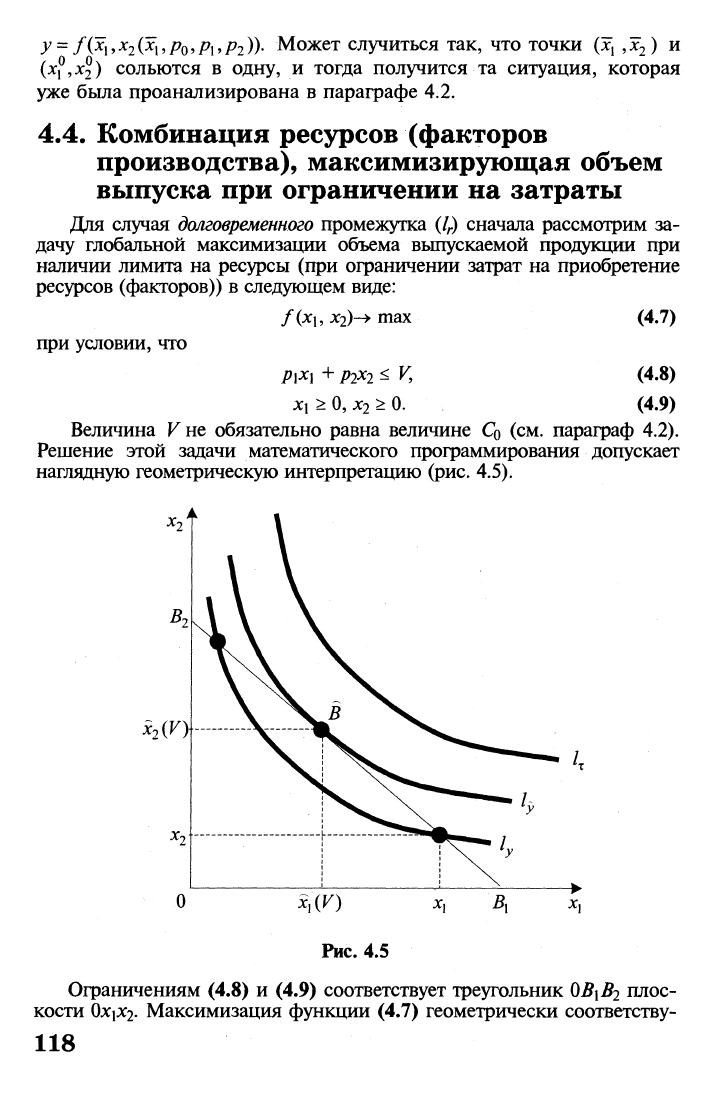
Решение этой задачи математического программирования допускает

наглядную геометрическую интерпретацию (рис. 4.5).

•^2

0 x,(V) х, В, х.

Рис. 4.5

Ограничениям (4.8) и (4.9) соответствует треугольник OBify плос-

кости Охрсг- Максимизация функции (4.7) геометрически соответству-

118

ет тому, что мы переходим на все более «северо-восточные» изокван-

ты,

пока они имеют еще общие точки с треугольником 0В\В

(прямая

В\В

имеет уравнение

р\Х\

—

V). Изокванты — гладкие линии,

выпуклые к точке 0 (а это так, ибоДх^ х

)

—

не произвольная функ-

ция двух переменных, а

производственная

функция, т.е. функция,

удовлетворяющая определенным требованиям гладкости и выпукло-

сти),

поэтому решению задачи (4.7)—(4.9) соответствует изокванта

1^,

которая касается гипотенузы (изокосты) В\В

в точке В. Любая

изокванта /

, расположенная «северо-восточнее» этой изокванты

(т > т), содержащей точку В, не подходит, ибо не имеет общих точек

с треугольником О!?^. Координаты х, (V) и x

(V) точки В дают ре-

шение задачи (4.7)—(4.9), ибо y

f(x

)<y

f(x

) (линия 1

у9

расположена «северо-восточнее» линии / (y

f(x

)).

В связи с тем, что это решение (х

{

(V),x

{V)) обращает ограни-

чение (4.8) в равенство р\

= V, вместо задачи (4.7)—(4.9)

можно рассмотреть более простую задачу на условный экстремум

Дх

)->тах (4.7)

при наличии ограничения

Р\Х{

Р2*2

= У

(jq > 0, х

0), (4.10)

заданного в виде равенства. (Эта задача была сформулирована выше в

параграфе 4.2).

Задачи (4.7)—(4.9) и (4.7), (4.10) разные, но решение (x,(F), x

(V))

у них одно и то же. Поскольку сумма р

х\ +

равна издержкам про-

изводства, постольку целесообразно заменить К на Си формально пе-

рейти к задаче максимизации объема выпускаемой продукции для

случая

долговременного

промежутка (/

) при

фиксированных издержках

производства

С (величина С играет роль параметра и не обязательно

равна величине Q (см. параграф 4.2):

/(*!, х

)-+

max (4.7)

при условии, что

Р\Х\ + />2*2= С/

(х,

> 0, х

0). (4.11)

Геометрическое решение задачи (4.7), (4.11) также наглядно очевидно

(рис.

4.6): следует переходить на все более «северо-восточные» изокванты

f(x

)) до тех пор, пока они продолжают иметь общие точки

(х

) с изокостой, соответствующей фиксированным издержкам про-

изводства С. Ясно, что решением задачи максимизации выпуска будет

точка (jq (C),x

(C)) касания последней из допустимых изоквант 1

фиксированной изокосты

р\Х\

р^к

= С Эта точка касания зависит от

величины издержек

(поэтому и написано (х

(С), х

(С)). Если издерж-

ки С изменятся, то изменится, вообще говоря, и точка (х

(С),х

(С)).

Множество точек (х

{

(С),х

(С)), соответствующих различным значение

119