Грачева М.В. и др. Моделирование экономических процессов
Подождите немного. Документ загружается.

В параграфе 4.2 в точке локального рыночного равновесия
(х
Х9
х
2
) был определен объем выпуска у
0
=
f(x
{
°
9
x
2
).
ЕСЛИ
В ограни-
чении (4.23) положить у
=
у
0
, то несложно показать, что x
x
(y
0
)
=
x
l9
х
2
(у
0
)
=
х
29
а также \х(у
0
)
=
Ро>
те
- множитель Лагранжа \л(у
0
) ра-
вен рыночной цене р
0
единицы выпускаемой продукции.
Имея выражение С = С(у\ выпишем в явном виде представление
прибыли PR(^) в случае долговременного промежутка как функции
объемов у выпускаемой продукции:
Ж(у) = РоУ-С(у),
Выражение FR(y)-р
0
у-С(у) играет важную роль в микроэко-
номике. Полезно сравнить это выражение с выражением для прибыли
фирмы в терминах объемов х
{
и х
2
затрачиваемых (используемых)
ресурсов в случае долговременного промежутка (см. параграф 4.1).
Пустая =\|/j(p
x
,p
2
,y\ x
2
=\\f
2
(p
l9
p
2
,y)
9
C = g(PuP
2
,y) —реше-
ние и значение задачи глобальной минимизации (4.22), (4.23).
Положим в задаче глобальной максимизации (4.7), (4.11) С
=
С, то-
гда, очевидно, х
]
=(р
]
(р
]9
р
29
С) = \у
]
(р
]9
р
29
у) = х
]9
х
2
=у
2
(р
и
р
2
,С) =
=
Щ(Р\>Р2>У)
=
Х2
и
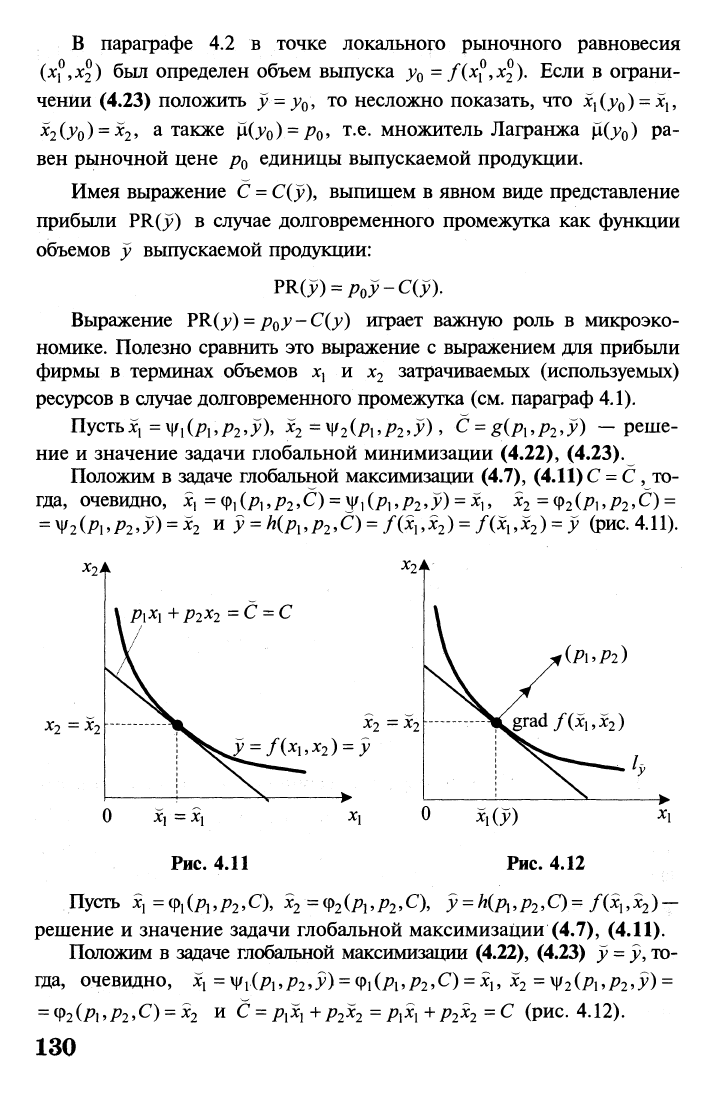
y = KP\>P2>C) = Axi,x
2
) = f(x
l9
x
2
) = y (рис. 4.11).
х
2+
Р\
х
\
+ Р2
Х
2 =С = С
х
2
—
х
2
х
2
х
2
—
х
2
= f(x
u
x
2
) = y
(Р\>Рг)
*\(У)
Рис.
4.11
Рис.
4.12
Пусть х
г
=ф
1
(/7
1
,/?
2
,С), х
2
=(р
2
(р
и
р
2
,С\ y = h(p
]
,p
2
,C)- f(x
]9
x
2
)
—
решение и значение задачи глобальной максимизации (4.7), (4.11).
Положим в задаче глобальной максимизации (4.22), (4.23) у = у
9
то-
гда, очевидно, х
х
= \\f
{
(p
x
,
р
2
9
у) =
ф!
(/?!,
р
2
,
С)
=
х
{
9
х
2
= \|/
2
(р
х 9
р
2
,у) =
=
(
?2(Р\>Р2>С)
=
Х2
и С =
р
х
х
х
+
р
2
х
2
=
р
х
х
х
+
р
2
х
2
= С (рис. 4.12).
130
Таким образом, наблюдается взаимозависимость задач (4.7), (4.11)
и (4.22), (4.23).
Задача глобальной минимизации издержек производства при фик-
сированном объеме у выпускаемой продукции для случая кратко-
срочного промежутка, когда фиксирован объем xj первого ресурса,
имеет вид (у играет роль параметра):
Р\Х\
+
р
2
х
2
=
C(xj,
х
2
)
(min) (4.27)
при условии, что
У
=
/(*.,
х
2
)
(4.28)
(х
{
>0).
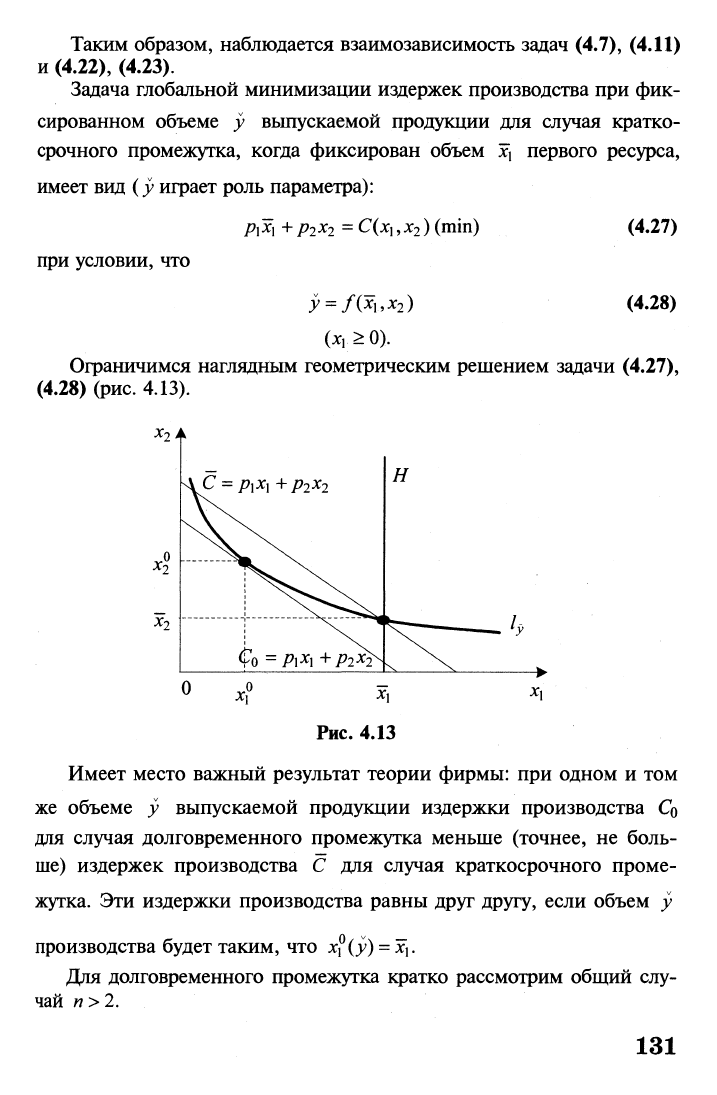
Ограничимся наглядным геометрическим решением задачи (4.27),
(4.28) (рис. 4.13).
х
2 А
Рис. 4.13
Имеет место важный результат теории фирмы: при одном и том
же объеме у выпускаемой продукции издержки производства Q
для случая долговременного промежутка меньше (точнее, не боль-
ше) издержек производства С для случая краткосрочного проме-
жутка. Эти издержки производства равны друг другу, если объем у
производства будет таким, что
х®(у)
- xj.
Для долговременного промежутка кратко рассмотрим общий слу-
чай п>2.
131

Задача (4.22), (4.23) глобальной минимизации издержек фирмы
при фиксированном объеме ее выпуска в общем случае имеет вид:
/*!*!+...
+
р„х„
= C(min) (4.29)
при наличии ограничения
j> = /(*,,...,*„)
(х, >0,...,JC„ >0). (4.30)
Для функции Лагранжа
L(x
l9
...
9
x
n9
\i)
= p
l
x
l
+...
+
p
n
x
n
+\i(y-f(x
l9
...
9
x
n
)) (4.31)
задачи (4.29), (4.30) на условный (локальный) экстремум условия
первого порядка имеют вид:
feHUo....,
^^
=
0,
^М)
= 0
(*
=
(*,
*„)),
дх
х
дх
п
д\х
или в развернутом виде
Рх
=цШ?±,...,
Рп
=Ж
y-f(x)
= 0
(*
= (*,,...,*„)).
(4.32)
дх
х
дх
п
Для производственной функции у = /(*), удовлетворяющей усло-
виям гладкости и выпуклости, критическая точка (х
{9
...
9
х
п9
\х) функ-
ции Лагранжа, взятая без последней координаты, т.е. точка
(x
l9
...
9
x
n
)
9
есть точка глобального условного минимума функций (4.29) при на-
личии ограничения (4.30).
Критическая точка (х
{9
...
9
х
п9
\х) функции Лагранжа является ре-
шением системы уравнений (4.32), поэтому при подстановке ее в эти
уравнения она обращает их в тождества:
Д-4^..,А,=Д-4^
{х
=
(х
{
,...,х
п
))
9
дх
х
дх
и
которые в компактной векторной форме имеют вид:
/? = pgrad/(x) (/? = (/?,,...,/?„)),
откуда следует, что в точке х
=
(х
{9
...
9
х
п
) изокванта выпуска у и
изокоста ((п -1) -мерная плоскость условных минимальных издержек)
касаются.
Функции x
]
=\^
l
(p
l9
...
9
p
n9
y)
9
...
9
x
n
=\\f
n
(p
l9
...
9
p
n9
y) являются функ-
циями условного спроса (по Хиксу) со стороны фирмы на рынках ресур-
сов.
Функция С = #(/>„...
9
р
п9
у)
= p
l
x
l
+...
+
p
n
x
n
=PiWi(P\,~>P„
9
У) +
•••
+
132

+p
n
v|/
w
(/?,,...,/?„,
j>)
представляет собой минимальные условные издерж-
ки фирмы.
Как и в случае и = 2, все функции x
l
=\\f
l
(p
l9
...
i
p
n
,y),...
9
x
n
=
=
Уп(Р\>—>Рп>У)
являются однородными нулевой степени по всем
переменным
р
и
...,р
п
,
а минимальные условные издержки фирмы
С = g(p\
9
...,p
n
,y) являются однородной функцией первой степени по
переменным
р
1
,...,р
п
.
Как и в случае п = 2, множитель Лагранжа
Д
= i|/
3
(A>
—>Р
п
>У)
яв
~
ляется скорее относительно большой величиной («слоном»).
4.6. Предельные (маржинальные)
свойства максимального выпуска
и минимальных издержек
Справедливы следующие важные равенства:
dh(p
l9
p
2
,C)
дС
•
=
Х; (4.33)
дкь.ъ.с):
£
^акъ.ъо
%
.
(434)
др
х
8р
2
dC(p
l9
p
29
y)
=fi;
(435)
ду
дс^.м) defray)
(4М)
fy\
д
Рг
Здесь h(p\, P2, О
=
Ах\
9
х
2
) — максимальное значение целевой
функции/xi, xi) задачи на условный экстремум (4.7), (4.11) (см. пара-
граф 4.1), С(р
и
р
2
,у)
=
р
{
х
х
+р
2
х
2
— минимальное значение целевой
функции С = р\Х\ +
р
2
х
2
задачи на условный экстремум (4.22) и (4.23)
(см.
параграф 4.5).
Равенства (4.34) называются тождествами Роя, равенства (4.36)
(которые также являются тождествами) представляют собой лемму
Шепарда. Левая часть равенства (4.33) есть предельный выпуск фир-
мы по лимиту. Из равенства (4.33) следует, что он равен множителю X
Лагранжа.
Проанализируем и докажем равенство (4.33).
133

Справедливо приближенное равенство:
dh(
P]
,p
2
,C) ^ h(p
{9
p
2
,C
+
AC)-h(p
u
p
2
,C)
дС АС
если величина АС относительно мала.
Из (4.33) и (4.37) следует, что
h(
Pl
,p
2
,C
+
AC)-h(
Pu
p
2
,C) „^
АС
откуда получаем
*0>1,
Ръ С+АС) - к(р
и
р
2
, Q
= ХАС .
(4.38)
Приближенное равенство (4.38) означает, что если лимит на ре-
сурсы
увеличится
на одну единицу (АС =1, которая относительно
мала),
то максимальный выпуск фирмы
увеличится
на величину, при-
ближенно равную множителю Лагранжа X, что естественно, ибо с
ростом величины С фирма увеличит объем приобретаемых на рынке
ресурсов и, следовательно, увеличит свой максимальный выпуск.
Следовательно, множитель X Лагранжа позволяет (приближен-
но) оценить новый условный максимальный выпуск
h(j>\,
ръ C+AQ
фирмы, если лимит С на ресурсы увеличился на относительно ма-
лую величину АС:
h(Pu
Ръ С + АС) £ h(p
u
р
ъ
Q + ^АС
.
(4.39)
Оценка А(р
ь
pj, C + AQ тем точнее, чем меньше АС.
Особо отметим, что нет необходимости решать новую задачу глобаль-
ной максимизации вьшуска фирмы при новом лимите С+
АС на
ресурсы,
ибо новый максимальный выпуск
дает
приближенная формула (4.39).
В связи с тем, что множитель Лагранжа X скорее мал, из при-
ближенного равенства (4.38) следует, что для значительного увеличе-
ния максимального выпуска требуется значительно увеличить АС
(прирост лимита на ресурсы).
Докажем равенство (4.33).
Конфигурация ресурсов jf, = щ(ри Ръ Q\
*2
=
Фг(Рь Ръ О при
подстановке в ограничение р
х
х\
+ДО2
=
С обращает его в тождество по
Р\,Р2,
С, т.е.
Рт(Ри Ръ Q +
PKPiiPh
Ръ О =
С.
(4.40)
В тождествах (но не в равенствах!) можно переходить к производ-
ным (к частным производным):
1 =£?£= n d<Pi(A>l2>
c
) д<р
2
(р
и
р
29
С)
DC
l
дС
2
дС
134

Имеем (используя теорему о частных производных сложной
функции):
dh(p
l9
p
2
,C)
=
д/(у
х
(р
х
,
р
2
,
С),
ф
2
(р
х
,
р
2
,
С))
=
#"(*!, х
2
)
=
ВС дС дС
&, 5С 5х
2
5С
!
дС
2
дС
*
дС
2
дС
т.е.
получили равенство (4.33).
В равенстве, отмеченном символом «*» (звездочка) были исполь-
зованы формулы:
дх
х
v
' дх
2
:
^1 (=^Ф1(А,Р2»
С
)); У*
2
=^2 (=^Ф2(Л>Р2>
С
))
(4.42)
(см.
(4.12) при х
х
=
х
х
,
JC
2
= i
2
,
A,
= X).
Проанализируем и докажем первое равенство (4.34).
Справедливо приближенное равенство:
dh(p
x
,p
2
,C) ^ h(p
x
+
Ap
x
,p
2
,C)-h(p
x
,p
2
,C)
др
х
~ Ар
{
если величина Ар
х
относительно мала.
Из (4.34) и (4.42) следует, что
КР\ + 4ft ,Р
2
>
с
) -
h
(P\ ,Р
2
, С) _
Л
г
= —Xi A ,
откуда получаем приближенное равенство:
h(p
x
+ Ар
х
, р
2
, Q ~ h(p
h
р
2
, Q = -х
х
Х Ар
х
. (4.43)
Приближенное равенство (4.43) означает, что если цена единицы
первого ресурса увеличится на одну единицу (Ар
х
= 1 и эта единица
относительно мала), то максимальный выпуск фирмы уменьшится на
величину, приближенно равную х
х
Х, что естественно, ибо при повы-
шении цены на первый ресурс фирма его приобретет в меньшем объ-
еме,
что, в свою очередь, уменьшит ее максимальный вьшуск.
Следовательно, Цроизведение х
х
Х позволяет (приближенно) оценить
довый максимальный вьшуск фирмы h(p
x
+
Ар
ъ
Р2,
С), если цена едини-
цы первого ресурса увеличится на относительно малую величину Ар
х
:
h(j>i
+ Ар
ь
р
2
, Q = h(p
h
р
2
, С) - х
х
Х Ар
{
. (4.44)
Оценка h(p
x
+ Лр
х
, р
2
, Q тем точнее, чем меньше Ар
х
.
135

Аналогично предыдущему случаю
нет
необходимости решать новую
задачу глобальной максимизации выпуска
при
новой цене
р
х
+
Ар
х
на
единицу первого ресурса,
ибо
новый глобальный максимальный
ус-
ловный выпуск
h(p\
+
A/?i,
р
ъ
Q
дает (приближенно) формула (4.44).
Докажем первое равенство
из
(4.34).
Найдем частные производные по
р\
всех слагаемых тождества (4.40):
рх
ду
х
(р
Х9
р
29
С)
+ ъ(рьръ
Q
+
р2
д^2(Р
11
Р2^1
=i£ =о,
др
х
др
х
др
х
откуда получаем
pl
db<J>i,P2,C)
+р2
дч>
2
(
Р]
,р
2
,С)
=
-
ъ(рьръ
Q.
(
4.45)
ty\
д
Р\
На основании теоремы
о
частных производных сложной функ-
ции имеем:
ЩР\
>Pi >
С)
=
5/(ф!
(д,
р
2
,
С),
ф
2
(р
х
,
р
2
,
С))
=
df(x
u
x
2
)
=
др
х
др
х
др
х
Sxj
9/?! 9х
2
др
х
др
х
др
х
др
х
др
х
=-Хц>
х
(р
х
,р
2
,С)
=
Л5с
х
,
Ибо Х
Х
= ф! (р
Ь
/?
2
, О-
Таким образом, первое равенство (4.34) доказано. Второе
ра-
венство (4.34) доказывается аналогично.
Равенство
(*)
аналогично равенству
(*) в
доказательстве равен-
ства (4.33).
Равенства (4.35)
и
(4.36) анализируются
и
доказываются анало-
гично.
Только
в
этом случае используются равенства (4.24)
при
Xi
—
Xi, X2 — Х
2
,
Л<
— JLI.
4.7. Максимизация выпуска фирмы
и минимизация ее издержек в случае
производственной функции
с постоянной эластичностью
замены ресурсов
Везде далее
а
0
>
0,
а
х
>
0,
а
2
>
0.
Производственную функцию
с
постоянной эластичностью
за-
мены ресурсов
(ПФ
ПЭЗР),fix\,
х^) =
ао(
а
\
х
\
а
+
а
2
х
2
а
У
я
а
следует
преобразовать
так:
136

A*i,*
2
)
= а
х
х
х
+а
2
х
2
Поэтому задача глобальной максимизации
Лх[,х
2
) ->тах,
Р\х\
+
Р2*2
= У
эквивалентна задаче глобальной минимизации (здесь а > 0, q
>
0)
а
х
х
х
а
+ а
2
х
2
а
-» min,
р
Х
Х
Х
+р
2
*2 = V.
Для задачи минимизации выписываем функцию Лагранжа
L = а
х
х
х
а
+a
2
x^
a
+ X(V
—
p\ Х\
—
р
2
х
2
)
и условия первого порядка для функции Лагранжа:
—
=
-аа
х
х
х
а
OXi
dL
Хр
х
- 0, = -аа
2
х
2
а
- Хр
2
= 0,
дх
1
дХ
=
V-p
x
x\
-p
2
x
2
= 0.
Имеем:
-ая,
х.
-a-l
1
Л
1
-аа
2
х
2
-a-l
~^Р\ _
-Ь-Рг х\
a+l
2 _ Р\
а
2
р
2
а
х
_. a+l _ Р\
а
2
v
a+l
•Х
7
=
Р\
а
2
р
2
а
х
a+l
ДС,.
Подставив выражение ддя х
2
в ограничение р
х
х\ + /?
2
Х2 = К, будем
иметь:
0=
V-piXi
-p
2
Р\
а
2
р
2
а
х
)
a+l
Х\
V(p
2
a,)
1_
a+l
•=>
^(^a^a+t +/7
2
(/?
1
a
2
)a+l
a+l /^a+1
F/7
2
a+1
a.
_L _1Л
(
A
a
a,)
a+,
+(P24)
a+1
^a+1
n
a+l
137
=
v
(<*A
a+l
Pi J
(p^)^
+
(p^a
2
)
a+l
:
9I(A^2^)-
Для x
2
имеем:
x, =
{P\
a
i)
a+l
V{PI*L)
a+l
2-
jj-*l j_ j_
(/>2*1
)
a+1
A (/Vl)
a+1
+ ft> (P\
a
2)
a+l
f \
=
v
Pi
Таким образом,
a+l 1
i —
= Ф2
(PuPl
>
V
\
(pfar^+ipZa^
f
a^
X =
\P\)
1
a+l
1
J_ _^_ _L _A_ '
X7 — •
^2
a+l
1 a
1 a '
a
a+l
p
a+l +
a
CL+\
p
*+\
y
=
h(p
{9
p
2
,V)
=
f(x
l
,x
2
)--
=
a
0
KPXJ
a+l
1 1
(A%)
a+1
+(p?*z)
a+1
+ач
( „ \
Pi)
a+l
1 1
138
= а
п
у-а
Г
_1_ J_V
a
/
\
Р\)
а+1
у-а
г j_ j_v
a
(^,)
а+1
+(лЧ)
а+1
( X
.Рг)
а+1
к
-а
I
1
_((
А
%)
а+,
+(^2%)
а+1
Г
а
-.-^
\Р\
а+1
/^
V
+ а
9
Рг)
а+1
=
а
п
А
1 i Y
(д
а
о,)^+(р
2
а
а
2
)^
1
а 1 a q
ца+l^a+l
+а
о+1ра+1)
а
=
= a
0
V>
1
Л
(А
а
Л.)
в+,
+0£«2)
а+1
(р,
а
«
1
)
а+1
+(Р2
а
«2)
а+1
:а
0
Г
^а+1
n
a+l i^a+l
п
а+1
"1
Z
7
!
+a
2 Pi
а+1
-<7-
f
1
=
a
0
V*
1
Y
tf,
a+,
/?f + а
2
а+1
/?2
(
i
>h(p
l
,p
29
V)
= a
0
V
i
!
1
Л
a,
a+1
/?f
+
а
2
а+1
/?2
139
