Грачева М.В. и др. Моделирование экономических процессов
Подождите немного. Документ загружается.

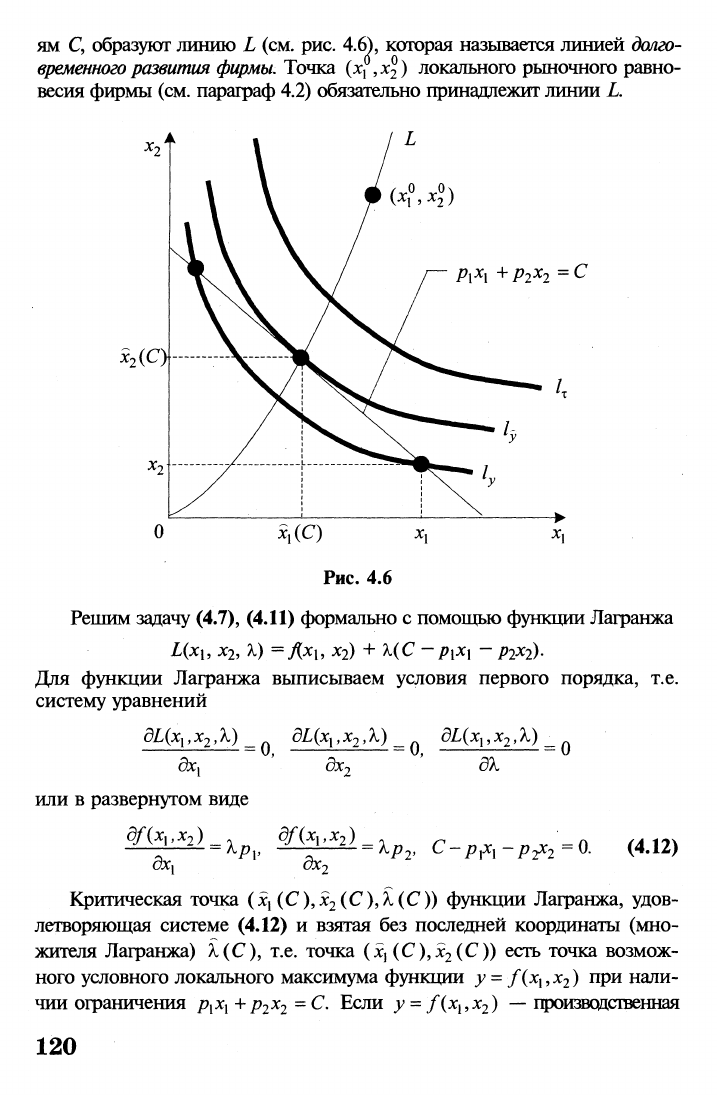
ям С, образуют линию L (см. рис. 4.6), которая называется линией
долго-
временного развития
фирмы.
Точка (х
{
,х
2
) локального рыночного равно-
весия фирмы (см. параграф 4.2) обязательно принадлежит линии L.
хЛ 1
L
х
2
(С)
1
1 \ W У
х
\
>
х
2)
\\\ х /
Г~
Р]Х
*
+Р2
*
2
=
\Л>^/^ '—•
/т
Л\д^-^
^— ' * — •
х
х
(С)
Рис. 4.6
Решим задачу (4.7), (4.11) формально с помощью функции Лагранжа
Цх
ь
х
2
,
X)
=А*ь х
2
) + ЦС -р\х
х
-
р
2
х
2
).
Для функции Лагранжа выписываем условия первого порядка, т.е.
систему уравнений
8L(x
x
,x
2
,X) дЬ(х
х
,х
2
,Х) дЬ{х
х
,х
2
,Х) _
дх
{
или в развернутом виде
дх
п
дХ
<№hib)
=
Xpv
df(x
x
,x
2
)
= Xp
^
С
-
Рх
х
х
-
Р
?
2
=0. (4.12)
дхл йх
9
Критическая точка (jq (С),
х
2
(С )Д (С)) функции Лагранжа, удов-
летворяющая системе (4.12) и взятая без последней координаты (мно-
жителя Лагранжа) Х(С), т.е. точка (х
х
(С),х
2
(С)) есть точка возмож-
ного условного локального максимума функции у = f(x
x
,x
2
) при нали-
чии ограничения
р
х
х
х
+р
2
х
2
=
С.
Если у
=
f(x
x
,x
2
)
—
производственная
120
функция, т.е. функция, удовлетворяющая условиям гладкости и выпукло-
сти,
то вьшолняются достаточные условия второго порядка локального
условного максимума функции (4.7) при наличии ограничения (4.11).
При этом точка (х
х
(С), х
2
(С)) условного локального максимума являет-
ся точкой условного глобального максимума функции (4.7) при наличии
ограничения (4.11). Если у =
f(x
x
,x
2
),
то х
х
(С)
> О,
х
2
(С)
> О,
Х(С)
>
0.
Подставив точку х
х
(С) > 0, х
2
(С)
>
0, ^(С)) в первые два равенства
системы (4.12), получим два тождества:
df(x
x
(C),x
2
(Q)
дх
х
df(5c
t
(C),x
2
(C))
dx?
= Х(С)
Рх
;
•ЧС)р
2
,
(4ЛЗ)
(4.14)
откуда следует коллинеарность градиента gradf((x
x
(C), x
2
(C)) и век-
тора цен р
=
(р
и
р
2
):
grad f((x
x
(C), х
2
(С))
=
ЦС)(
Рх
,
р
2
)
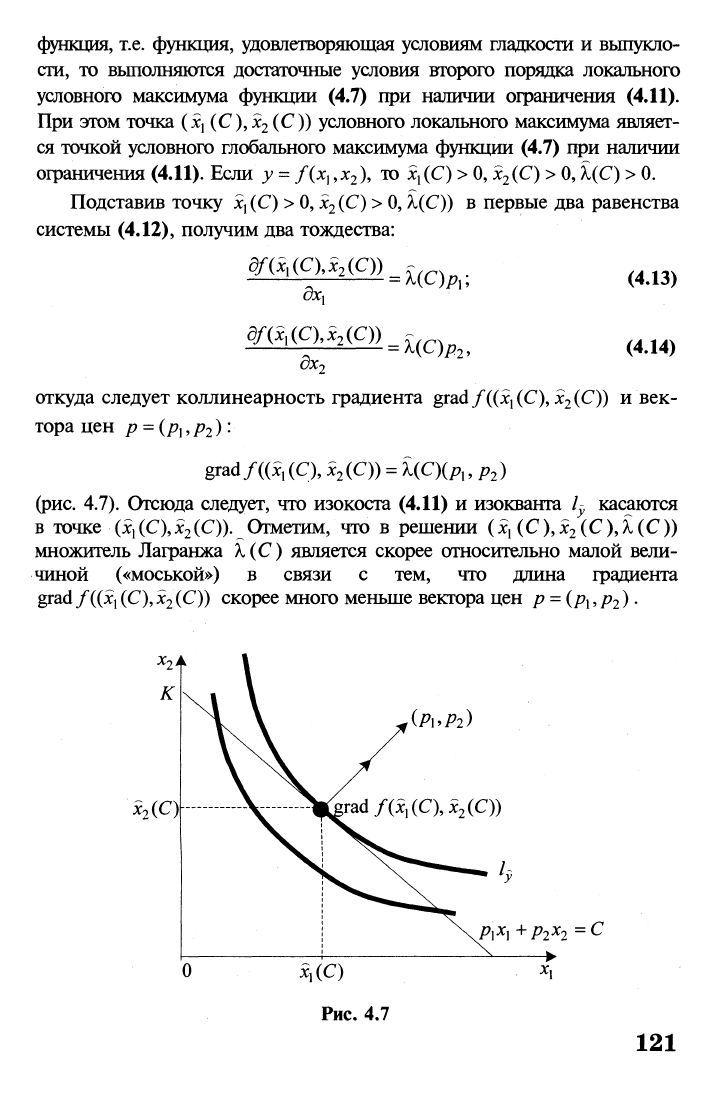
(рис.
4.7). Отсюда следует, что изокоста (4.11) и изокванта Ц касаются
в точке (х
х
(С\х
2
(С)). Отметим, что в решении (х
х
(С),х
2
(С)Д (С))
множитель Лагранжа Х(С) является скорее относительно малой вели-
чиной («моськой») в связи с тем, что длина градиента
gradf((x
x
(C\x
2
(C)) скорее много меньше вектора цен р
=
(Р\,р
2
)-
х?А
х
2
(С)\
(PuPi)
f(x
x
(C\x
2
(Q)
р
х
х
х
+
р
2
х
2
=
С
121

Если положить р
п
=
- , то для задачи глобальной максимиза-
Х(С)
ции прибыли
Pof(
x
\
>
х
2)
-
(Р\
х
\
+
Pi
x
2) = PR -> max
условия первого порядка (4.1) приобретут вид:
_ Qf(xi,X2) _ „ „ df(xi,x
2
)
__
_
PO—Q^—PP Ро-ъГ-Pr
1
откуда, принимая во внимание равенство р
0
=- , эти условия
ЦС)
первого порядка следует переписать так:
— =ЦС)/?
г
, — = Л(С)р
2
.
ОХ\ ОХ2
Этой системе уравнений удовлетворяет х
х
=х
х
(С) и х
2
=х
2
(С)
((4.13) и (4.14)). Следовательно, решение х,(С) = х
1
°,х
2
(С) =
Х2
пред-
ставляет собой локальное рыночное равновесие фирмы при
р
0
=-
, т.е. решение (jt,(C),3c
2
(C)) задачи (4.7), (4.11) условной
Х(С)
глобальной максимизации совпадает с решением (х{\х
2
) задачи
глобальной максимизации прибыли, если цена р
0
выпускаемой
фирмой продукции равна р
0
= - .
Таким образом, предложена естественная экономическая ин-
терпретация множителя Лагранжа ЦС).
В параграфе 4.2 в точке локального рыночного равновесия (х
{
°
9
х
2
)
фирмы были определены издержки Q = р\
х
х
+ р
2
х
2
. Если в ограни-
чении (4.11) положить С = Q, то очевидно
х
}
(Co) = xf , х
2
(Q) = х
2
,
а также - =
/?
п
,
т.е. величина, обратная множителю Лагранжа
X
(С
0
),
ЧСо)
равна рыночной цене р
0
единицы выпускаемой фирмой продукции.
Подставив х
{
(С), х
2
(С) в выражение у = J{x
h
xfc), получим, что
у = /(х
1
(С),х
2
(С)) = ДС), (4.15)
122

т.е.
получим, что максимальный выпуск y = F(C) фирмы по существу
есть функция издержек С. Выражение (4.15) является
значением
зада-
чи (4.7), (4.11).
Так построенная функция у = F(C) соответствует случаю долго-
временного
промежутка.
Имея функцию у = F(C), можно выписать выражение для при-
были в терминах
издержек
PR(C) = p$F(C) - С (сравнить с выраже-
нием для прибыли фирмы в терминах
затрачиваемых (используемых)
ресурсов,
см. параграф 4.2).
Таким образом, задача максимизации прибыли фирмы в случае
долговременного промежутка может иметь три постановки:
• в терминах объемов х
х
и х
2
затрачиваемых (используемых) ре-
сурсов:
РоА*ь *2> ~Р\Х\ ~
Р2*2
= PR(*b *2> -> шах;
• в терминах объема у выпускаемой фирмой продукции:
А) У
~
С(У)
= PRO
7
) -> max;
• в терминах издержек С фирмы:
/>
0
ДС) - С = PR(C) -> max.
Строго говоря, координаты х
{
(С) и х
2
(С) являются функциями
всех параметров
р
х
,р
2
,С
задачи (4.7), (4.11), т.е. х
х
=
у
х
(р
х
,р
2
,С),
х
2
=ц
2
(р
х
,р
2
,С).
Эти функции называются функциями условного
спроса
(по
Маршаллу)
со стороны фирмы на ресурсы. Фирма предъ-
являет спрос на каждый ресурс на рынке этого ресурса. Спрос на-
зывается
условным,
потому что есть условие
р
х
х
х
+р
2
х
2
=С, которое
появляется в связи с лимитом на ресурсы. Отметим также, что
Ъ =
у
3
(р
{
,р
2
,С).
Максимальный выпуск/(х
х
,х
2
) фирмы имеет вид:
у = /(х
х
,х
2
)=/(щ(р
х
,
Р2,
С),
(р
2
(Р\,Р2,
С) = h(p
h
p
2
, С).
Выписанная функция представляет собой условное предложение
фирмой своего выпуска на рынке выпускаемого ею продукта.
Функции условного спроса (по Маршаллу) х
х
=
<р
х
(р
х
,р
2
,С),
х
2
=<р
2
(р
х
,р
2
,С) и функции условного предложения фирмы
y
=
h(p
x
,p
2
,C) однородны нулевой степени, т.е. для любого числа
у
> 0 справедливы равенства:
<Pi
(УА,
УА>
>
УС)
=
cpi
(А,
Р
2
,
С),
ф
2
(ур
х
,
УР
2
, уС) = ф
2
(А > Pi > Q,
Kw\ > Wi, УО
=
К
р
х
, р
2
,
с).
123
С одной стороны, задача глобальной максимизации (4.7), (4.11)
имеет решение щ{р\,р
2
,С\ (р
2
(р
]9
р
2
,С), задача глобальной макси-
мизации (4.7) при наличии ограничения ур
х
х
х
+
ур
2
х
2
=
уС имеет ре-
шение <Р\(ур\,ур
2
,уС),
<Р
2
(УР\>УР
2
>уС)-
С другой стороны, эти две за-
дачи глобальной максимизации эквивалентны (сократив ограничение
УР\
Х
\
+УР2
Х
2
- У С
на
У 9
получим ограничение (4.11)), поэтому
9I(YA>YP2>YO = 9I(A>/?2>
C
)>
<Р2(УР\>УР2>УС) =
Ч>2(Р\>Р2>
С
)-
Равенство й(УА,ур
2
,уС) = h(p
l
,р
2
,С) также очевидно, ибо
%A>Y/?2>YO
=
/(9I(YA>Y/?2>YO>
<P2(YPi,Y/?2>YC))
=
-f($\(P\>Pl>
C
\
<P2(Pl>P2>
C
))
==h
(Pl>P2>
C
)-
Задача максимизации объема выпускаемой фирмой продукции
при фиксированных издержках С для случая краткосрочного промежут-
ка (s
r
), когда лимитирован объем xj первого ресурса, имеет вид:
f(x
x
, х
2
) -» max (4Л6)
(4.17)
при условии, что
РЛ
+ Р2
Х
2
=
С
(Х
2
>
0).
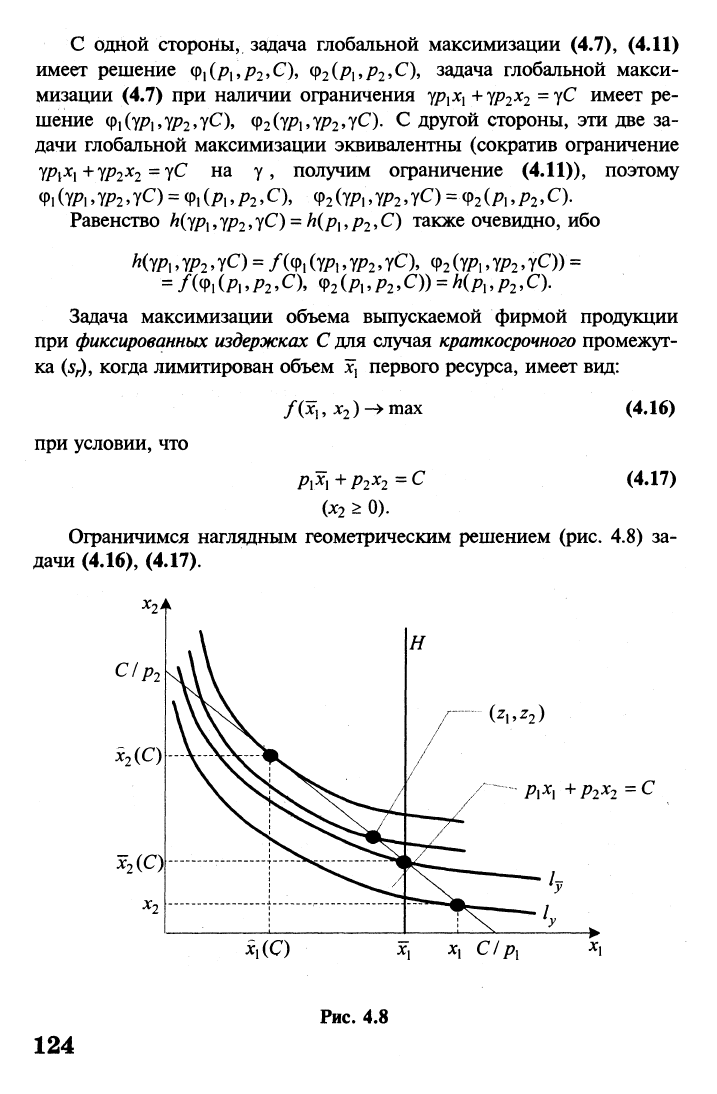
Ограничимся наглядным геометрическим решением (рис. 4.8) за
дачи (4.16), (4.17).
X
2
i
С1р
2
х
2
(С)
х
2
(С)
х
2
к
1
х
4
***—-^*.
Ч
^
4
^/
Я
/ (z
l9
z
2
)
/ РЛ +Р2
/
/
'\У
-Si—
h
г^—
•>
,
*i(C)
х, CIр
х
*\
124
Рис. 4.8

Перемещаемся
по
изоквантам
1
у
(у
=
f{x
x
,x
2
))
на
«северо-восток»
до того момента, пока изокванта 1у
(у
=
f(x
x
,x
2
))
не
пройдет через
точку (х
х
,х
2
(С))
9
которая
и
есть решение задачи (4.16), (4.17).
От
этой изокванты
Ц
далее
на
«северо-восток» идти нельзя, ибо
в
точках
z —
(z
b
z
2
)
пересечения новых изоквант
и
фиксированной изокосты
Р\Х\
+
/?2*2
==
С имеет место неравенство
2
Х
ФХ
Х
.
Если
бы
условия
х\ =
х
х
не
было,
то
решением задачи максимиза-
ции объема выпускаемой продукции была
бы
точка
(х
х
(С),Зс
2
(С)),
которая соответствует случаю долговременного промежутка. Очевид-
но,
/
(
JCJ
(С),
х
2
(С))
>
f
(3cj,
х
2
(С)),
ибо
изокванта, проходящая через
точку (х
1
(С),Зс
2
(С)), расположена «северо-восточнее» изокванты,
проходящей через точку /(х
х
, х
2
(С).
Получен важный результат теории фирмы:
при
одних
и тех же
издержках
С
объем выпускаемой фирмой продукции
в
случае долго-
временного промежутка больше (точнее
не
меньше) объема выпускае-
мой фирмой продукции
в
случае краткосрочного промежутка.
Эти объемы сравняются, если издержки производства
С
будут
та-
кими,
что
х
х
(С) = х
х
.
Вертикальная прямая
х\ = х
х
называется лини-
ей краткосрочного развития фирмы (см. рис. 4.8).
Для долговременного промежутка кратко рассмотрим общий
случай п
>
2.
Задача (4.7), (4.11) глобальной максимизации выпуска фирмы
при лимите на ресурсы в общем случае имеет вид:
/(*!,...,*„)-» max (4.18)
при наличии ограничения
р
х
х
х
+...
+
р
п
х
п
=С
(4.19)
(х,>0,...,^>0).
Для функции Лагранжа
Цх
х
, ...,х
п
)
=
f(x
x
,
...
9
х
п
)
+
Х(С-<р
х
х
}
-...
-р
п
х
п
) (4.20)
задачи (4.18), (4.19)
на
условный (локальный) экстремум условия
первого порядка имеют вид:
дЦх,Х) _ аЦхД)
дЦх,Х)
__
дх
х
дх
п
ЭХ
(х
=
(х
х
,...,х
п
))
или
в
развернутом виде:
dL(x,X) dL(x,X)
— =
Vi>->
— =
*р
2
.
С
-Л
дс
1---Л
дг
я=
0
<
4
-
21
>
дх
х
дх
п
(х
=
(х
]9
...,х
п
)).
125

Для производственной функции
у
=
f(x)
9
удовлетворяющей усло-
виям гладкости
и
выпуклости, (x
l9
...
9
x
n9
X) — критическая точка
функции (4.18)
при
наличии ограничения (4.19).
Критическая точка (x
l9
...
9
x
n9
X) функции Лагранжа является
ре-
шением системы уравнений (4.21), поэтому
при
подстановке
ее в эти
уравнения
она
обращает
их в
тождества:
дЦх
9
Х)
~
дЦх
9
Х)
~ „ „
— =
^р,,...,—
=
Хр
п
(х
=
(х
19
...
9
х
п
)
9
дх
х
дх
п
которые
в
компактной векторной форме имеют вид:
grad/(x)
= V (p
=
(p
l9
...
9
p
n
))
9
откуда следует,
что в
точке x==(x
l9
...
9
x
n
) изокванта максимального
выпуска
и
изокоста
((п
-1) -мерная плоскость постоянных издержек)
касаются.
Функции
х
х
=q>!(p
l9
...
9
p
n9
С),...,х
п
=
ср„(р
и
...
9
р
п9
С) являются функ-
циями условного спроса
(по
Маршаллу)
со
стороны фирмы
на
рынках
ресурсов. Функция
у
=
h(p
l9
...
9
р
п9
С) = f(x
{9
...
9
x
n
)
=
f(q>i(#,».,/>„,C\...
9
Ф„(p
l9
...,р„,С)) есть функция предложения фирмы
на
рынке
вы-
пускаемой фирмой продукции.
Как
и в
случае
п
=
2 все
функции x
l
=<p
l
(p
l9
...
9
p
n9
C)
9
...
9
х
п
=<Рп(Р\>->Р*>
с
)>-
У
=
ЧР\9->Р
п
>С) являются однородными нуле-
вой степени
по
всем переменным
р
Х9
..:
9
р
п9
С.
Как
и в
случае
л = 2
множитель Лагранжа Х
=
<р
3
(р
]9
...
9
р
п9
С)
яв-
ляется скорее относительно малой величиной («моськой»).
4.5. Комбинация ресурсов (факторов
производства), минимизирующая
издержки при фиксированном (общем)
объеме выпуска
Для случая долговременного промежутка
(1
Г
)
рассмотрим задачу
глобальной минимизации издержек
при
фиксированном объеме
у вы-
пускаемой продукции:
Р\Х\
+
Р2Х2
—
С (х\
9
Х2)->
min (4.22)
при условии,
что
y=f(x
h
x
2
)
(4.23)
(*i
> 0, х
2
>
0).
126
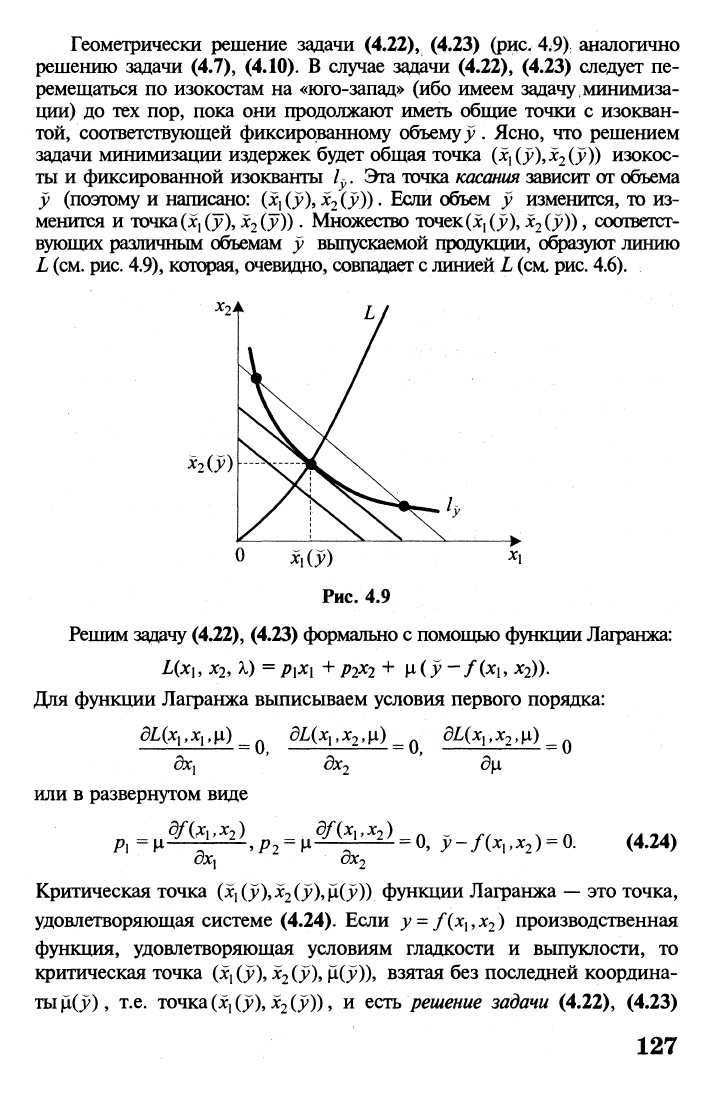
Геометрически решение задачи (4.22), (4.23) (рис. 4,9)
;
аналогично
решению задачи (4.7), (4.10). В случае задачи (4.22), (4.23) следует пе-
ремещаться по изокостам на «юго-запад» (ибо имеем задачу.минимиза-
ции) до тех пор, пока они продолжают иметь общие точки с изокван-
той, соответствующей фиксированному объему .у . Ясно, что решением
задачи минимизации издержек будет общая точка (х
х
(у),х
2
(у)) изокос-
ты и фиксированной изокванты Ц. Эта точка касания зависит от объема
у (поэтому и написано:
(х
х
(у),
х
2
(у)).
Если объем у изменится, то из-
менится и точка(х
х
(у),
х
2
(у)).
Множество точек(х
х
(у\
х
2
(у)),
соответст-
вующих различным объемам у выпускаемой продукции, образуют линию
L (см. рис. 4.9), которая, очевидно, совпадает с линией L (см. рис. 4.6).
*2'
*2 09
0 х
х
(у) *i
Рис.
4.9
Решим заддчу (4.22), (4.23) формально с помощью функции Лагранжа:
Цх\, х
2
, X) = р\х
х
+
р
2
х
2
+ ii(y~f(x\, х
2
)).
Для функции Лагранжа вьшисываем условия первого порядка:
ЭЦхрХрц) Щх
1
,х
2
,\х) _ • дЦх
х
,х
2
,\л) _^
дх
х
дх
2
д\х
или в развернутом виде
df(x
x
,x
2
) df{x
x
,x
2
) ~ ~ s,
ч л
,л<%л\
р
х
=\х
Jy
?
2
\p
2
= »
J
\
l 2
=0,
y-f(x
x
,x
2
)
=
0. (4.24)
ох
х
ох
2
Критическая точка (x
x
(y),x
2
(y)
9
]i(y)) функции Лагранжа — это точка,
удовлетворяющая системе (4.24). Если y
=
f(x
l9
x
2
) производственная
функция, удовлетворяющая условиям гладкости и выпуклости, то
критическая точка
(х
х
(у),
х
2
(у\ Д00)> взятая без последней координа-
ты
ДСу),
т.е. точка(х
х
(у)
9
х
2
(у))
9
и есть решение задачи (4.22), (4.23)
127
глобальной минимизации издержек при данном фиксированном объ-
еме выпуска у. Подставив координаты точки
(х
х
(у)
9
х
2
(у),\х(у)) в
первые два уравнения системы (4.24), получим два тождества:
_^df(x
u
x
2
) _
ri
df(x
l
,x
2
)
Р\
- и ~ у Рг -
у>
dXi
дх>у
(4.25)
которые в компактной векторной форме можно переписать так:
(р
х
,
р
2
) =
Д
grad
/(*,, x
2
).
(4.26)
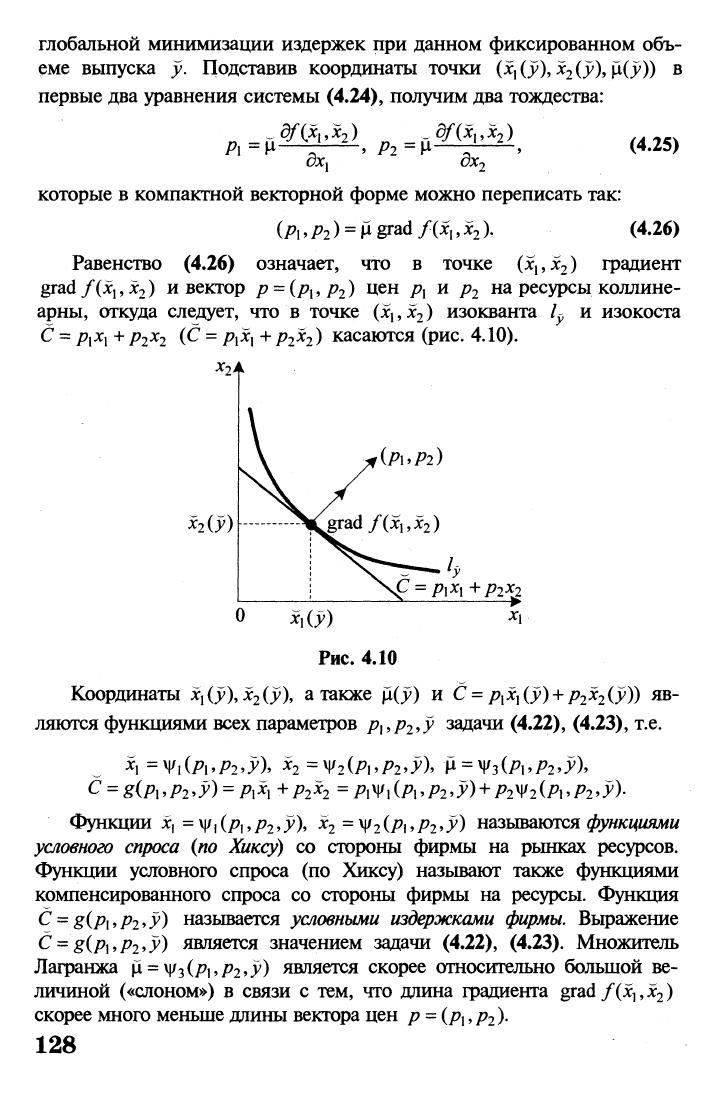
Равенство (4.26) означает, что в точке (х
Х9
х
2
) градиент
grad f(x
X9
х
2
) и вектор р
=
(р
х
, р
2
) цен р
х
и р
2
на ресурсы коллине-
арны, откуда следует, что в точке (х
Х9
х
2
) изокванта Ц и изокоста
С =
р
х
х
х
+ р
2
х
2
(С =
р
х
х
х
+
р
2
х
2
)
касаются (рис. 4.10).
Х
2
А
(РиРг)
ЫУ)
ЫУ)
Рис. 4.10
Координаты
х
х
(у%х
2
(у),
а также ji(y) и С
=
р
х
х
х
(у)
+
р
2
х
2
(у))
яв-
ляются функциями всех параметров
р
х
>р
2
,у
задачи (4.22), (4.23), т.е.
х
х
=У
х
(Р1,р
2
,У)>
x
2
=\]f
2
(p
x
,p
29
y),
& = Уз(Р\>Р2>У)>
С = g(P\
>Рг*У) =
Р\Х\
+
р
г
х
2
=
РхЧ\
(р
х
,р
2
>У) +
РгУг (Р\>Рг >
У)-
Функции х\ =\\!
х
(р
х
,р
2
,у), х
2
=у
2
(р
]9
р
29
у)
называются функциями
условного спроса
(по Хиксу) со стороны фирмы на рынках ресурсов.
Функции условного спроса (по Хиксу) называют также функциями
компенсированного спроса со стороны фирмы на ресурсы. Функция
С = g(p
x
,p
2
,y) называется
условными издержками
фирмы.
Выражение
С
=
g(p
x
,p
2
>y) является значением задачи (4.22), (4.23). Множитель
Лагранжа
\л =
^^(р
]9
р
29
у) является скорее относительно большой ве-
личиной («слоном») в связи с тем, что длина градиента grad/(x
1
,jc
2
)
скорее много меньше длины вектора цен р
=
(р
х
, р
2
).
128

Функции х\ -
\j/,
(p
x
, p
2
, y), x
2
=
\\f
2
(P\, Ръ
У)
условного спроса (по
Хиксу) однородны нулевой степени по переменным д и р
2>
а
функция С
=
g(P],p
2
,y) условных издержек однородна первой сте-
пени по переменным р
х
и р
2
.
Действительно, задача глобальной минимизации (4.22), (4.23)
имеет решение
У\(р\
9
р
29
у)
и х
2
=у
2
(Р\
9
р
29
у)
9
задача глобальной
минимизации ур
х
х
х
+
ур
2
х
2
=yC(min) при наличии ограничения (4.23)
имеет решение \|/, (ур
х
,
ур
2
,у) и
\\f
2
(ур
х
, ур
2
, у)- Однако эти две задачи
глобальной минимизации эквивалентны, ибо вторая получается из
первой умножением целевой функции
р
х
х
х
+
р
2
х
2
=
С на число у > 0.
ПОЭТОМУ Vi(yPi
9
yp
2
,y)
=
V\(Pi>P2>y)
И
У2(УР\>УР2>У) =
У2(Р\>Р2>У)-
Однородность первой степени функции С = g(p
x
,p
2
,y) условных из-
держек очевидна:
g(YP\,yP2>y) =
yP\V\(Wi>yP2J)
+
W2^(Wi>W2>y) =
= y(P\V\(yP\,yP2>y)
+ P2V2(YP\>yP2>y)) =
yg(P\>P2>y)'
Если положить р
0
=
Д, то для задачи глобальной максимизации
прибыли
Pof(*\
>
х
2)
- (Р\
х
\ + Р2
Х
2) = PR -> max,
условия первого порядка (4.1) приобретают вид:
„ д/(х\Л
2
)_ „ „ д/(х
х
,х
2
) _ _•
Ро I ~^' Р° а -
Р2>
дх
х
дх
2
откуда, принимая во внимание равенства р
0
=
Д, эти условия первого
порядка следует переписать так:
rt
df(x
x
;x
2
) _ _ ~df(x
l9
x
2
)_ „
И " -
Р\>
И
I -Л-
Этой системе уравнений удовлетворяют jq = х
х
и х
2
= х
2
(см. ра-
венства (4.25)). Следовательно, решение х
х
=х
х
, х
2
= х
2
представляет
собой локальное рыночное равновесие фирмы при р
0
=
Д, т.е. реше-
ние (х
х
,х
2
) задачи (4.22), (4.23) условной глобальной минимизации
совпадает с решением (xf, x
2
) задачи глобальной максимизации при-
были, если цена р
0
выпускаемой фирмой продукции равна р
0
=
Д.
Таким образом, предложена естественная экономическая интер-
претация множителя Лагранжа
Д
= \л(р
х
, р
2
, у).
129
