Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications
Подождите немного. Документ загружается.

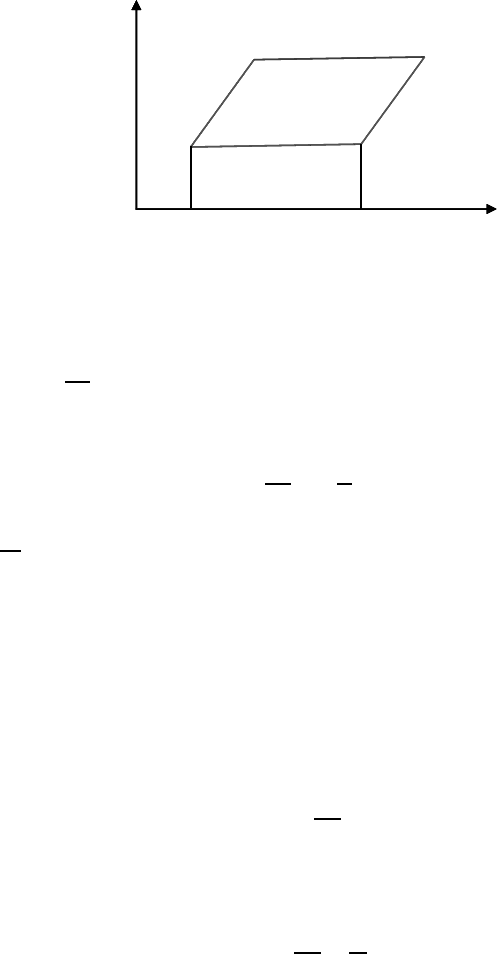
598 8Solutions
A
B
C
D
S
1
S
2
S
γ
A
B
C
D
S
1
S
2
S
γ
FIGURE 8.1
Carnot’s cycle for a thin film.
The ratio
Q
ΔS
, as mentioned previously, is the specific heat to form a unit of
area of the grain boundary.
Finally, the expression for the temperature coefficient of grain boundary
surface tension reads
dγ
dT
= −
q
T
(8.4)
It is known from experiment that q is positive (it is absorbed by a surface),
so
dγ
dT
is negative.
At last we would like to emphasize one issue. It is clear that it is impossi-
ble to change the area of a grain boundary independently of the bulk of the
grains. However, it should be intimated that the change in the area of a liquid
film is connected with the interaction between the surface layer and the bulk
of the liquid film as well; there is no surface in the uncombined state.
PROBLEM 1.2
The number of grain boundaries over the length of the rivet is equal to
n =
D
0
(8.5)
Then the change of the length of the rivet in the course of annealing (due to
graingrowth)canbeexpressedas
Δ
gg
=
1
D
0
−
1
D
V
ex
(8.6)
The change of the length of the rivet due to thermal expansion of Al reads
Δ
T Al
= αΔT (8.7)
© 2010 by Taylor and Francis Group, LLC
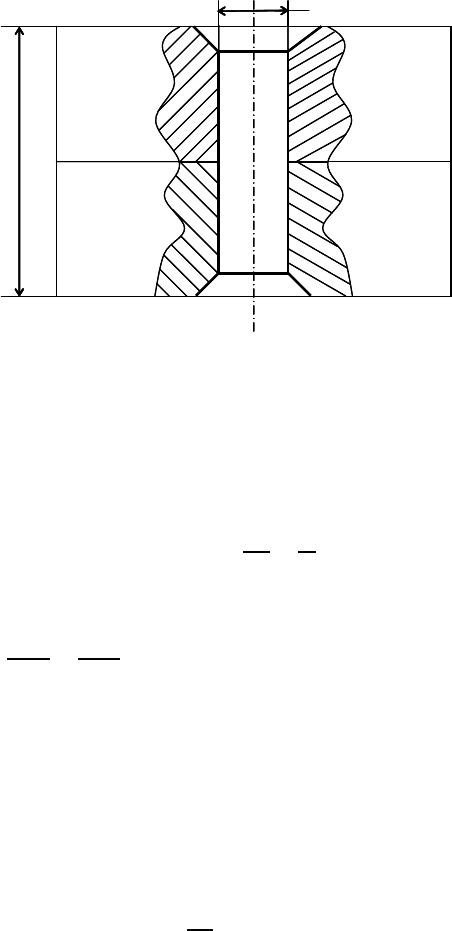
8Solutions 599
d
d
FIGURE 8.2
Diagram of two pieces of material connected by a rivet.
From Eqs. (8.6) and (8.7) we arrive at the expression for the resulting change
in length of the rivet
¯
Δ =Δ
gg
− Δ
T Al
=
1
D
0
−
1
D
V
ex
− αΔT
(8.8)
For the values of the parameters given in the problem we arrive at
¯
Δ =
1
10
−8
−
1
10
−7
· 1.35 · 10
−10
− 2 · 10
−5
· 200
=8· 10
−3
(8.9)
One can see that the total shortening of the rivet is rather large, in the range
of 1% of the length. The stresses which occur in the rivet depend on the
thermal expansion of the connected materials as well
¯
Δ =Δ
gg
− Δ
T Al
− (Δ
T Al
− Δ
T con
) (8.10)
where the term Δ
T con
describes the thermal expansion of the connected ma-
terials. For the simplest case (the last term on the right-hand side of Eq. (8.10)
is zero) we obtain
σ = E
¯
Δ
=8· 10
−3
E (8.11)
We stress that the major peculiarity of the construction proposed is the pos-
sibility of controlling the value of the stresses matching the initial and final
mean grain size.
PROBLEM 1.3
© 2010 by Taylor and Francis Group, LLC
600 8Solutions
1. Using the Henry isotherm for adsorption of vacancies at the grain boundary
we arrive at
zBc
eq
v
= V
ex
(8.12)
where z is the adsorption capacity of the grain boundary, B = B
0
exp
Q
kT
is
the adsorption constant, c
eq
v
is the equilibrium concentration of the vacancies.
Considering the width of the grain boundary equal to three atomic layers,
the adsorption capacity can be defined as
z =
3
(2.86 · 10
−10
)
2
=3.6 · 10
19
at/m
2
=6· 10
−5
mol/m
2
(8.13)
The adsorption constant B can be defined as
B =
V
ex
zc
eq
v
=
V
ex
z
(c
eq
v
)
−1
(8.14)
One can see that the adsorption heat Q is equal to the enthalpy of vacancy
formation in the bulk H
f
.ForAlH
f
=0.76 eV, S
f
=0.7K.Fora40
◦
111
grain boundary in Al V
ex
=6.4 · 10
−6
mol/m
2
. Then at the melting temper-
ature B =6.2 · 10
2
.
2. The enrichment coefficient β is equal to
β =
Γ
zc
eq
v
= B (8.15)
Let us plot this value against the volume solubility of the vacancies (c
eq
v
)on
the Seah-Hondros diagram (Fig. 1.3) for the melting temperature. Evidently,
the agreement is poor.
3. All our calculations were carried out in the framework of the simplest
adsorptional isotherm — the Henry isotherm. Let us extract the value B
from the Zhuchovitskii-McLean isotherm (1.144). Then
zBc
eq
v
1 − c
eq
v
+ Bc
eq
v
= V
ex
(8.16)
and
B =
V
ex
(1 − c
eq
v
)(c
eq
v
)
−1
z − V
ex
(8.17)
For T = T
m
we obtain B = 712. Comparing this result with the previous one,
which was derived in the framework of the Henry isotherm, one can see that
the difference is in the range of ∼ 10%.
PROBLEM 1.4
1. The excess grain boundary free volume V
ex
fora40
◦
111 tilt boundary
canbeexpressedasV
ex
= −Γ
0
Ω
0
=6.4 ·10
−11
m
3
/m
2
. In other words, every
grain boundary increases the size of a polycrystal by Δδ =6.4 · 10
−11
m. Let
© 2010 by Taylor and Francis Group, LLC

8Solutions 601
us consider a cubic sample with the side of the cube equal to L. Under the
assumption that the grains are uniform and cubic as well with the grain size
a we arrive at
V = L
3
;
L = L
0
+
L
a
Δδ
and
L =
L
0
1 −
Δδ
a
∼
=
L
0
1+
Δ δ
a
(8.18)
where L
0
is the size of a side of the corresponding single crystal.
2. The free energy of polycrystals can be expressed as
G = G
s
+ G
grav
(8.19)
where G
s
is the surface (grain boundary) part of the free energy, G
grav
is the
gravitational part of the free energy.
The total number of grains in the polycrystal can be represented as
N =
L
3
0
1+
Δδ
a
3
a
3
(8.20)
(N 1).
The total grain boundary area is equal to
S =
1
2
6Na
2
=
3
a
L
3
0
1+
Δδ
a
3
(8.21)
and, respectively, the “grain boundary” part of the free energy is equal to
G
s
=
3
a
γL
3
0
1+
Δδ
a
3
(8.22)
γ is the grain boundary surface tension.
The gravitational part of the free energy of the polycrystal can be repre-
sented as follows: for a polycrystal which rests on a support
G
grav
I
=
1
2
L
0
1+
Δδ
a
V
0
ρg (8.23)
for the suspended polycrystal
G
grav
II
=
H
0
−
1
2
L
0
1+
Δδ
a
V
0
ρg (8.24)
where V
0
is a volume of the corresponding single crystal, ρ is the density of
the perfect crystal, g is the gravity acceleration.
© 2010 by Taylor and Francis Group, LLC
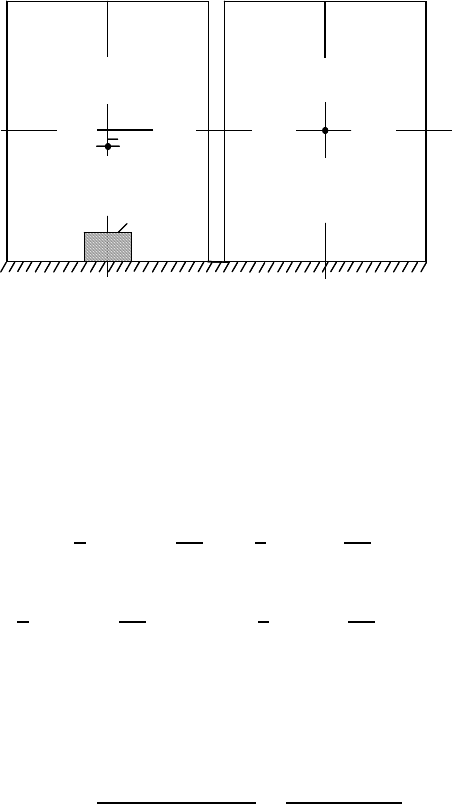
602 8Solutions
h
sugar
h
sugar
(a)
(b)
FIGURE 8.3
Two glasses with water and sugar: (a) a piece of sugar in water; (b) sugar is
dissolved in water.
The expression for the free energy of the polycrystal can be written corre-
spondingly as
G
I
=
3
a
γL
3
0
1+
Δδ
a
3
+
1
2
L
0
1+
Δδ
a
V
0
ρg (8.25)
G
II
=
3
a
L
3
0
γ
1+
Δδ
a
3
+
H
0
−
1
2
L
0
1+
Δδ
a
V
0
ρg (8.26)
One can see that for the polycrystal which rests on the support (Eq. (8.25))
there is no equilibrium grain size, the minimum of the free energy is achieved
at a →∞.
The relation for the equilibrium grain size for the suspended polycrystal
reads
a
∗
=
L
3
0
γΔδ
L
0
ΔδV
0
ρg − 3L
3
0
γ
∼
=
γΔδ
L
0
Δδρg − 3γ
(8.27)
A positive value of a
∗
can be obtained only for L
0
≥ 10
6
m.
3. In the examples considered the system includes the polycrystal and the
earth. The position of the center of masses of this system — the polycrystal
+ the earth — remains unchanged. To better understand the core of the prob-
lem let us consider a cylindrical glass with tea and a piece of sugar (Fig. 8.3).
The center of gravity of the glass with the undissolved piece of sugar is sit-
uated a little bit below the geometrical center of the glass due to the larger
density of sugar in comparison to water.
When the sugar dissolves in water the center of the gravity rises by the
distance h. However, the position of the system the earth + the glass remains
© 2010 by Taylor and Francis Group, LLC
8Solutions 603
unchanged. In cosmic space during dissolution the glass will change its po-
sition with respect to the coordinates connected with the earth, the sun or
the stars. The energy of this motion is the reduction of the free energy of the
system due to the formation of the dissolution of sugar in water.
The situation with a polycrystal is in perfect analogy with the considered
one. The annealing of the homogeneous polycrystal will lead to a single crystal
with the same coordinates of the center of masses, whereas the polycrystal
with grains distributed along the length will change the position of the center
of the masses in the course of grain growth.
PROBLEM 1.5
1. The change of the melting temperature can be evaluated by Eq. (1.203)
ΔT
∼
=
γ · T
m
qD
(8.28)
where q is the specific heat of melting. For Al q =10
9
J/m
3
, γ =0.45 J/m
2
and for D =10nmΔT is equal to
∼
=
0.05 T
m
. The melting temperature for
the nanocrystalline sample considered is 0.05 T
m
lower than that for a single
crystal of Al.
2. To derive the Clausius-Clapeyron equation for a nanocrystalline material
we do not have to consider an equal chemical potential of the two phases —
solid and liquid — but the free energy of the polycrystal and of the relevant
amount of liquid. If N is the number of atoms in the polycrystal, we arrive at
Nμ
s
+ Aγ= Nμ
(8.29)
where μ
s
and μ
are the chemical potentials of the atoms in the solid and
liquid, respectively. A is the total grain boundary area of the polycrystal. We
neglect hereby the surface energy of the nanocrystalline specimen in the liquid
state.
Then
N
∂μ
s
∂T
p
dT + N
∂μ
s
∂P
T
dP + A
∂γ
∂T
p
dT + A
∂γ
∂T
T
dP
= N
dμ
∂T
p
+ N
dμ
∂p
dp (8.30)
Taking into account that −
∂γ
∂T
p
= S
b
is the grain boundary entropy and
∂γ
∂p
= V
ex
is the excess volume,
1
relation (8.30) can be expressed as
[N ΔS
L−S
− AS
b
] dt =[N Ω
L−S
− AV
ex
] dP (8.31)
1
We would like to remind the reader that the grain boundary excess free volume (Chapter 1)
is equal to V
ex
= −Γ
0
Ω
s
ˆ
m
3
/m
2
˜
where Γ
0
is the autoadsorption.
© 2010 by Taylor and Francis Group, LLC
604 8Solutions
The Clausius-Clapeyron equation for the nanocrystalline sample then reads
dP
dT
=
q
T
−
A
N
S
b
ΔΩ −
A
N
V
ex
(8.32)
The grain boundary entropy is on the order of ∼−10
−3
J/m
2
K.
The ratio
A
N
can be extracted from the following considerations. If spherical
(or cuboidal) grains are assumed, the total grain boundary area of a sample
with volume V is equal to
A =
3V
D
(8.33)
and the total number of atoms N canbeexpressedas
N =
V
1 −
3 V
ex
D
Ω
s
(8.34)
and the ratio
A
N
reads
A
N
=
3Ω
s
D
1 −
3 V
ex
D
(8.35)
Finally, the Clausius-Clapeyron relation for nanocrystals can be expressed as
dP
dT
=
q
T
+
3Ω
s
D
[
1−3
V
ex
D
]
·
∂γ
∂T
p
ΔΩ −
3Ω
s
V
ex
D
[
1−
3 V
ex
D
]
(8.36)
One can see that the impact of grain boundaries can change qualitatively the
behavior of the system at the melting point. This is evident from the influence
of the denominator of Eq. (8.36). Actually, the grain boundary excess free vol-
ume decreases, and “compensates” the change of the atomic volume during
melting of “normal” metals, where ΔΩ
L−S
> 0 and promotes the “abnormal”
behavior in cases that ΔΩ
L−S
< 0(Bi,Ga).
3. Let us consider Eq. (8.36) for nanocrystalline Al. As can be seen the ef-
fect connected with the grain boundary excess free volume does not change
essentially the numerator of (8.36), so the expression (8.36) can be rewritten
as
dT
dP
=
ΔΩ
Ω
s
−
3V
ex
D−3V
ex
q
Ω
s
· T (8.37)
For D =7nm
dT
dP
∼
=
4.5 · 10
−3
Ω
s
q
and for D =25nm
dT
dP
∼
=
0.05
Ω
s
q
T
© 2010 by Taylor and Francis Group, LLC

8Solutions 605
For D = 5 nm the melting temperature decreases with increasing pressure,
like for water, Ga, Bi; for D = 7 nm the melting temperature is nearly inde-
pendent of pressure, and for D = 25 nm the polycrystal qualitatively behaves
like a coarse-grained Al polycrystal.
PROBLEM 2.1
In order to determine the surface tension of the low-angle tilt grain boundary
let us invoke the Read-Shockley relation (2.3) in a form which is convenient
for calculation
γ = γ
0
ϕ (A
0
− lnϕ) (8.38)
where
γ
0
=
μb
2π(1 − ν
),A
0
=0.5
For 112 tilt grain boundaries the Burgers vector b =
a
2
110,wherea =
4.5 · 10
−10
m is the lattice constant; b =
a
√
2
2
=2.86 · 10
−10
m
μ =26.46 Pa
Then for ϕ =0.5
◦
we obtain γ =0.082 J/m
2
,forϕ =3
◦
γ =0.323 J/m
2
,for
ϕ =5
◦
γ =0.46 J/m
2
,forϕ =8
◦
γ =0.62 J/m
2
.
PROBLEM 2.2
For mechanical equilibrium at a triple junction, given that the grain bound-
ary surface tension does not depend on the orientation of the boundaries, the
surface tensions should satisfy Young’s theorem (1.162)
γ
1
sinα
1
=
γ
2
sinα
2
=
γ
3
sinα
3
Then, the desired angles should satisfy the system of equations
α
1
+ α
2
+ α
3
=2π
γ
1
sinα
1
=
γ
3
sin (2π − α
1
− α
3
)
γ
1
sinα
1
=
γ
3
sinα
3
For the given values of grain boundary surface tension
α
1
= 150
◦
α
2
= 103
◦
α
3
= 107
◦
© 2010 by Taylor and Francis Group, LLC

606 8Solutions
PROBLEM 2.3
As stressed in Sec. 1.4.1 grains in a polycrystal play the role of a source of
pressure to confine a boundary in the deformed state. It was mentioned as
well that since the material in a grain boundary is stretched the pressure p
0
applied to a grain boundary should be negative: p
0
< 0. Thus, our problem
is reduced to a quantitative evaluation of the pressure which is necessary to
confine a liquid layer at a temperature which is much lower than the melting
point.
The Clausius-Clapeyron equation in our case reads
dP
dT
=
ΔH
L→S
T Δ
L−S
(8.39)
where ΔH
L→S
is the change in enthalpy of the two phases at the melting
point
ΔH = H
solid
− H
liquid
(8.40)
ΔH
L−S
T
=ΔS
L−S
(8.41)
The enthalpy change is identical to the specific heat of melting, ΔΩ is the
change in the atomic volume at the melting point.
To study Eq. (8.39) in a rather wide temperature range the dependencies
ΔH
L−S
(T )andΔV
L−S
(T ) should be known
dH
L−S
=ΔCpdT +Δ[Ω(1− T
α
)] dp (8.42)
where
Δc
p
= c
sol
p
− c
liq
p
(8.43)
is the difference of the specific heat for the liquid and solid phase, respectively,
ΔV (1 − Tα)=
Ω
solid
1 − Tα
solid
−
Ω
liquid
1 − Tα
liquid
(8.44)
However, for our purpose — the evaluation of the pressure — we will ignore
the change in the enthalpy and atomic volume with temperature.
Then, from Eq. (8.39) we arrive at
ΔP = P − P
0
=
q
ΔΩ
ln
T
T
0
(8.45)
where q is the specific heat of melting, P
0
is the atmospheric pressure (1 atm).
Using the reference values for the parameters of (8.45) we obtain
Al :ΔP = −5.4 · 10
4
atm
∼
=
−5.4GPa
Pb :ΔP = −2.2 · 10
3
atm
∼
=
−0.22GPa (8.46)
Au :ΔP = −9.4 · 10
5
atm
∼
=
−9.46GPa
© 2010 by Taylor and Francis Group, LLC

8Solutions 607
α
a
b
αα
a
b
FIGURE 8.4
Configuration of a 2D quadruple junction (bold lines) and an energetically
more favorable configuration (thin lines).
Such negative pressure should act from the bulk on the grain boundary to
confine it as a liquid.
PROBLEM 2.4
Let us consider a quadruple junction in a 2D square (Fig. 8.4). The length of
the sides is a.
The total length of the grain boundaries which form the quadruple junction
(bold lines) is equal to L
0
=2a
√
2.
However, the same grains can be connected in another way, namely as shown
in Fig. 8.4. In this case the total length of grain boundaries, which border the
grains, is equal to
L =2a
1
sinα
+ a −
a
tanα
(8.47)
This length reaches the minimal value at α =60
◦
. Indeed:
dL
dα
= −
2cosα
sin
2
α
+
1
sin
2
α
= 0 (8.48)
The new length of the grains is equal to
L =
4a
√
3
+ a −
a
√
3
=
√
3+1
∼
=
2.73a (8.49)
while the initial length is equal to L
0
∼
=
2.83a. In other words, the new con-
figuration is energetically more acceptable.
We would like to draw the attention of the reader to the point that the dif-
ference between the initial and energetically favorable length is rather small.
© 2010 by Taylor and Francis Group, LLC
