Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

628 8Solutions

If the particles are rather small then their motion should be controlled by

interface diﬀusion (see Sec. 3.5), and the particle mobility can be expressed

(r)=

πr

(8.168)

where δ is the eﬀective thickness of the surface layer, δ

∼

−9

m, D

an interface diﬀusion coeﬃcient (D

∼

−11

/s), Ω is an atomic volume

(Ω = 10

−5

/mol). Finally, the expression for the criterion λ

part,b

reads

part,b

4δD

rkTc<D>m

(8.169)

Taking <D>for the initial grain microstructure equal to <D>

∼

3·10

−5

we obtain

part,b

∼

0.2 (8.170)

The results of the computer simulation of grain growth in Al at the same

values of the parameters [623] are expressed in the time dependency of the

mean grain size <D>. Basically the criterion λ is the ratio of the rate of

grain growth under the action of a drag factor and free grain growth. In other

words, we should ﬁnd the ratio of

d<D>

for the grain growth with the mobile

particles and in the case of a pure grain boundary. The results for diﬀerent

<D>are given in Table 8.1. One can see that the agreement between the

evaluation given by Eq. (8.169) and the experiment is reasonable.

TABLE 8.1

Eﬃciency of Grain Growth Inhibition by Second-Phase Particles

<D> λ

part,b

from Eq. (8.169) from computer simulation [623]

7 · 10

−5

m 0.1 0.36

5 · 10

−5

m 0.14 0.16

PROBLEM 3.11

Let us consider the grain growth inhibited by second-phase particles. If the

particles are rather small there are two ways of inhibiting grain growth: Zener

drag, where the interaction between particles and grain boundary reduces

the driving force of grain growth, and the joint motion of particles and grain

boundary.

For the sake of simplicity we consider the single size distribution. Using

relation (3.61) (see Chapter 3) the grain growth kinetics for Zener dragging

canbeexpressedas

d<D>

= m



<D>

−

3cγ



(8.171)

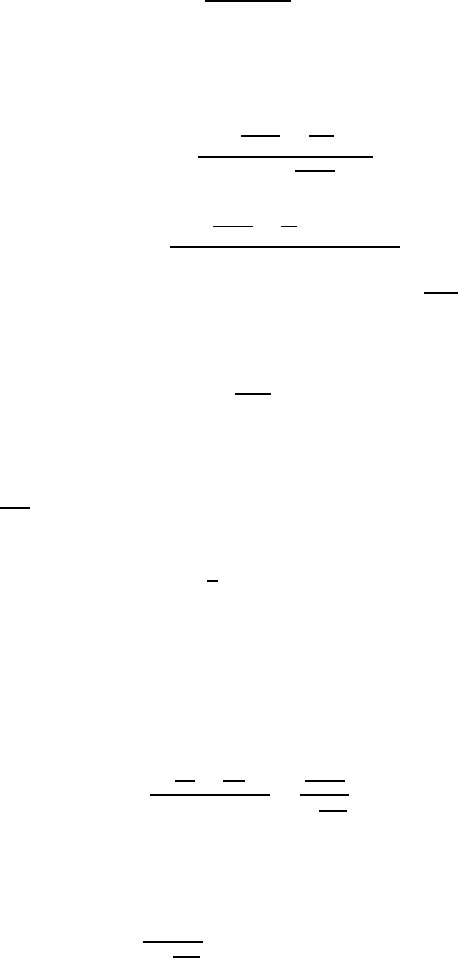
8Solutions 629

where <D>is the mean grain diameter of the polycrystal.

The grain growth kinetics for the joint motion of grain boundary and par-

ticles is given by Eq. (3.71) (see Chapter 3)

V =

γm

)

<D>n

(8.172)

is the number of the particles per unit area of the boundary. The criterion

λ, which determines the relative eﬃciency of these two ways of dragging (see

Chapter 6) can be constructed as

Zener, part



<D>

−

3cγ



)

<D>

(8.173)

Zener, part



<D>

−



<D>

)

(8.174)

The number of particles per unit area of the boundary n

2πr

.Forrather

small particles the dominant mechanism of the mass transfer is interfacial

diﬀusion; that is why the particle mobility is inversely proportional to r

(Chapter 3, Eq. (3.35))

πr

(8.175)

The expression for λ

Zener, part

can be transformed into

Zener, part

= M



− 3cr

<D>



(8.176)

where M =

Relation (8.176) has a minimum at

c<D> (8.177)

Such radius of second-phase particles in a single size distribution complies

with the maximal relative eﬃciency of Zener drag.

PROBLEM 3.12

1. The slope of the line H/k−lnA

can be determined by analytical geometry

— the straight line which passes through two points

−

lnA

− lnA

ΔH

(8.178)

where H

, H

, A

are the activation enthalpies and the pre-exponential

factors of the two considered grain boundaries, respectively.

For grain boundaries I and II we arrive at

ΔH

kln

= 672 K (399

◦

C) (8.179)

630 8Solutions

for grain boundaries I and III the compensation temperature is equal to 681

K (408

◦

C) and for the pair II-III boundaries T

= 667 K (394

◦

C).

1. Let us now ﬁnd the compensation temperature as the point of intersection

of two (or more) kinetic dependencies in coordinates ln

−

,namely

x + B

y + C

x + B

y + C

= 0 (8.180)

+lnA

− lnA

= 0 (8.181)

Solution by matrix algebra yields

, lnA

(8.182)

or for the pair GBI–GBIII we arrive at

1 −4.6

1 −9.2

1.62 · 10

1.92 · 10

, lnA

−4.61.62 · 10

−9.21.92 · 10

1.62 · 10

1.92 · 10

(8.183)

−9.2+4.6

1.62 · 10

− 1.93 · 10

=1.48 · 10

−3

−1

= 674 K (401

◦

C); A

=4· 10

−9

/s.

For the grain boundaries II-III and I-II we get, respectively,

= 667 K(394

◦

C; A

=2· 10

−9

= 676 K(403

◦

C; A

=3· 10

−9

2. The condition that three grain boundaries intersect in one point is

= 0 (8.184)

− B

− C

− A

− B

(8.185)

The sum in Eq. (8.185) is equal to ∼ 592.

Eq. (8.185) gives an assessment of the deviation of the pair intersection

points from the virtual triple point. It is noteworthy that the magnitude of

every term in (8.185) is in the range of 10

. So the intersection points are very

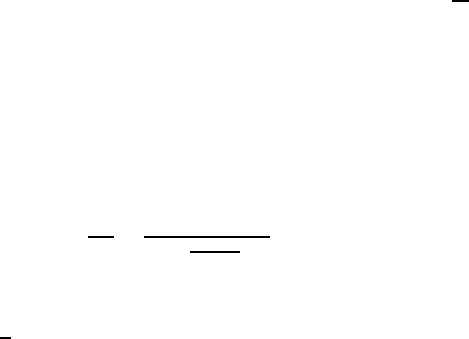
8Solutions 631

close to each other.

3. The mobilities of the grain boundaries at 320

◦

C are equal, respectively:

GBI : A

=1.3 · 10

−10

GBII : A

=2.0 · 10

−11

GBIII : A

=2.4 · 10

−7

The mobilities of these grain boundaries at 520

◦

Care

GBI A

=1· 10

−7

GBII A

=1.0 · 10

−6

GBIII A

=2.4 · 10

−7

At a temperature lower than T

the boundaries with low energy of activation

are most mobile, whereas at temperatures higher than T

grain boundaries

with a high energy of activation are the fastest ones.

PROBLEM 3.13

From Eq. (3.234) we arrive at

m = m

(1 − αV ) (8.186)

where m

is the grain boundary mobility without magnetic ﬁeld α =

σ

From Eq. (8.186) we obtain the relation for the grain boundary mobility in

a magnetic ﬁeld in the case that the driving force of grain boundary motion

is a capillary driving force

m = m

[1 − α (mγκ)] (8.187)

where κ is the curvature.

Then the kinetic equation for grain growth in a polycrystal in a magnetic

ﬁeld reads



αm



(8.188)

and the time dependency for the mean grain radius R can be expressed as



−−R



+ αm

γ (R − R

)=m

γt (8.189)

where R

is the mean grain radius at t = 0. (The mean grain size (twice the

radius R) and the radius of the curvature of the moving grain boundary are

not identical. Here we do not make a distinction between these parameters

since we are looking for a qualitative result.)

It should be stressed that, as describedinChapter3,thereareseveralcon-

tributions to the total drag force, some of which can be characterized by a

strong dependency of the mobility change on the grain boundary migration

rate. Eq. (8.186) represents the simplest one.

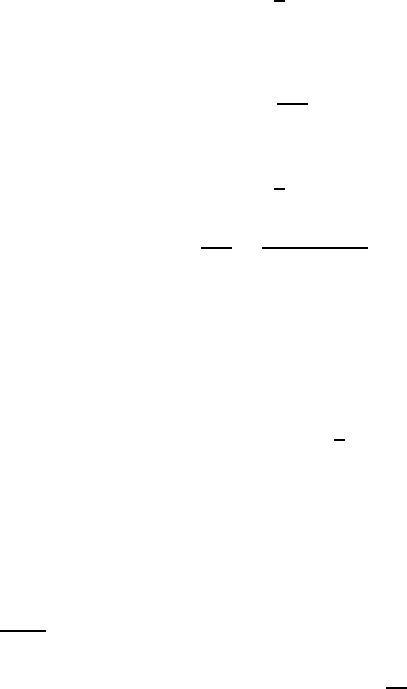
632 8Solutions

PROBLEM 4.1

(a) The volume fraction c of the particles is equal to

c =

πr

∼

4 · 10

−3

Then the maximum pinning force

3cγ

=6· 10

J/m

(b)

c =

πr

N =5·10

−3

3cγ

3 · 10

−3

· 0.5

5 · 10

−9

=1.4 · 10

J/m

(8.190)

PROBLEM 4.2

(a) If a spherical particle with radius r intersects a triple line the total reduc-

tion of grain boundary energy and the line energy of the triple junction can

be expressed as

ΔG = γ



1 −

πr



− 2rγ



(8.191)

where γ



is the line tension of the triple junction.

Correspondingly, the maximum attraction force f

∗

=3πrγ +2γ



(8.192)

The particles in contact with the triple junction are conﬁned to a volume

π(2r)

.1m=πr

, i.e. the number of particles per 1m of triple junction length

is equal to

¯n = πr

· N =

(8.193)

Thus, the maximum pinning force f

∗

max

∗

max

=¯nf

∗

L (8.194)

where

L is the length of the triple junction per 1 m

of a grain boundary.

The number of a triple junctions N

in a polycrystal per unit volume is

equal to [551]

≈ 12n (8.195)

where n is the number of grains per unit volume.

Let us consider the grains as spheres with diameter <D>. Then the

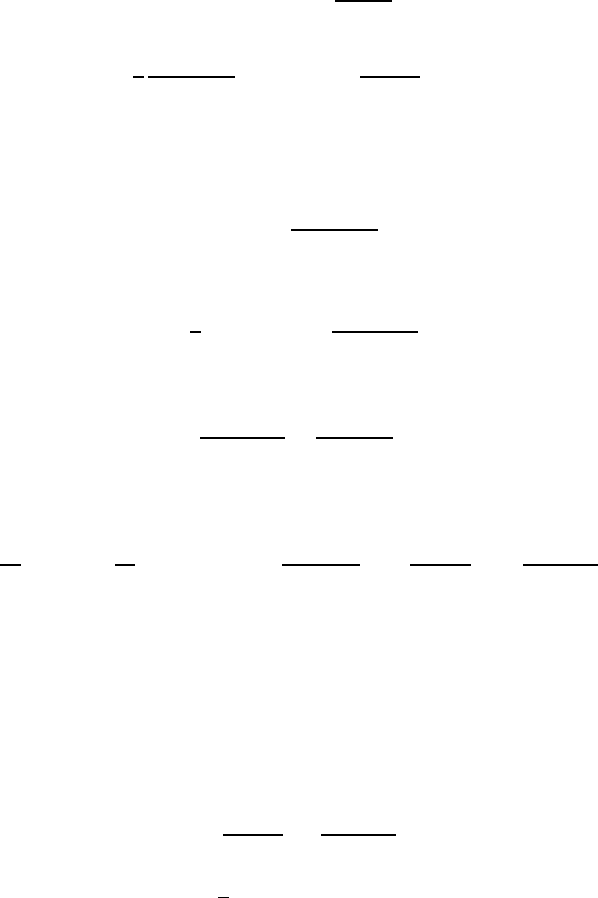
8Solutions 633

number of grains per unit volume is equal to

π<D>

and the total area of the

grain boundaries is

π<D>

· π<D>

<D>

(8.196)

The coeﬃcient 1/2 is introduced due to the fact that one boundary belongs

to two grains.

Then N

can be expressed as

=12n =

π<D>

(8.197)

The total length of the triple junctions per unit volume can be evaluated as

∼

<D>N

π<D>

(8.198)

The desired ratio of the length of the triple junctions to grain boundary area

L reads

L =

3/<D>

π<D>

(8.199)

Finally, the maximal pinning force by particles on triple junctions can be

expressed as

· f

∗

L =



3πrγ +2γ





π<D>

∼

γc

<D>

+6·



r<D>

(8.200)

∼

50 · 10

J/m

+25· 10

J/m

∼

5.3 · 10

J/m

(8.201)

As can be seen for the given parameters, the pinning force of the particles on

the triple junctions is at least an order of magnitude smaller than the pinning

force from the particles on the grain boundary. The general pinning force is

equal to the sum of these pinning forces. The force f

is the pinning force

when the particles are located exactly on the triple line.

(b) The pinning force is equal to (see Eq. (8.201) in the previous problem):

=25

γc

<D>



r<D>

c =

πr

∼

5 · 10

−3

∼

9 · 10

J/m

634 8Solutions

PROBLEM 4.3

(a) If a spherical particle with radius r is located at a quadruple point the

total reduction of the grain boundary energy can be expressed as

ΔG = γ



1 − 2πr



(8.202)

Since nothing is known about the energy of a quadruple junction we assume

that we can neglect the eﬀect of this parameter on the energetics of the system.

From (8.202) we obtain the maximum attraction force f

∗

=4πrγ (8.203)

If we assume that a quadruple junction can be occupied by only one particle,

then the maximum pinning force f

will be equal to

=4πrγc ·

quad

(8.204)

where

quad

is the number of quadruple junctions per unit grain boundary

area.

The number of quadruple junctions in a polycrystal with n grains per unit

volume is equal to [551]

quad

∼

6n (8.205)

Since n =

π<D>

,where<D>is the diameter and 3/<D>is the total

grain boundary area per unit volume

quad

π<D>

(8.206)

and

quad

36 <D>

π<D>

·3

π<D>

(8.207)

Then for the maximum pinning force f

we arrive at

=4πrγc

N =

64πr

γN

<D>

(8.208)

Substituting the parameters given in the problem we come to

∼

J/m

(8.209)

Note that the force f

depends very strongly on the size of the second-phase

particles.

(b) Substituting the parameters of the problem into Eq. (8.208) yields

=10

J/m

8Solutions 635

PROBLEM 4.4

The total grain boundary area of a sample with the mean grain size <D>

is equal to

S =

<D>

(8.210)

On the other hand, the rate of grain boundary motion is equal to

R =

mγ

(8.211)

where R is the radius of the curvature of the moving boundary; R ∼<D>.

Then

= −

<D>

d<D>

∼−

3mγ

<D>

∼−

mγS

(8.212)

PROBLEM 4.5

The rate of grain area change is given by the Von Neumann-Mullins relation

= −A

[2π − n(π − 2θ)] (8.213)

As shown in Chapter 4 for a system with triple junctions of ﬁnite mobility

the angle θ is a function of the dimensionless parameter Λ (Λ =

). The

equilibrium value θ = π/3 is obtained for Λ →∞

γ(n − 6) (8.214)

To ﬁnd the dependence of the grain area change rate for Λ = ∞ aconsidera-

tion of the relation (8.213) in the vicinity of “equilibrium” (θ = π/3) can be

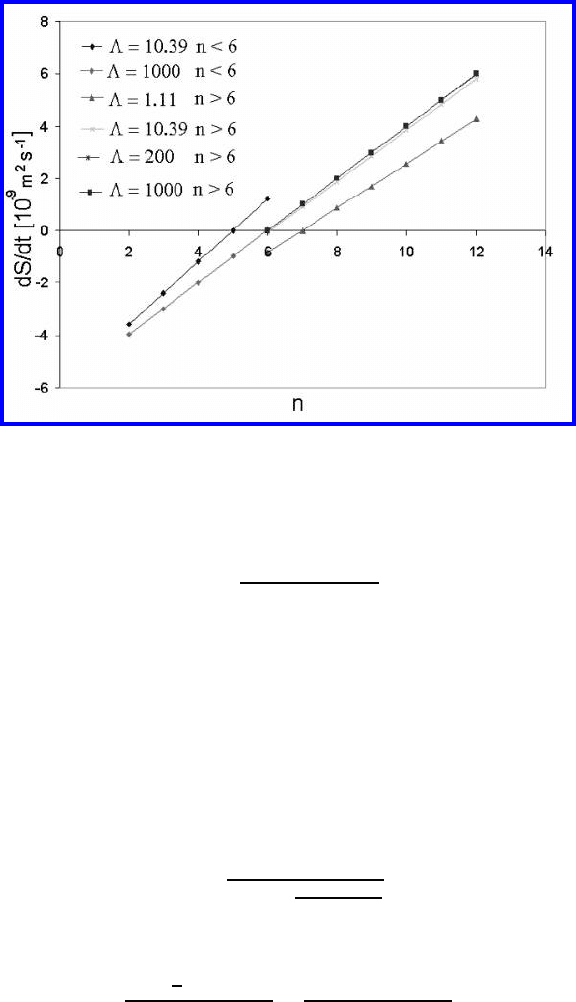
invoked (Eqs. (4.82) and (4.85)). The diagram of

for diﬀerent Λ is given

in Fig. 8.10.

For Λ

∼

10 and grains with n<6 the topological class which meets the con-

dition

= 0 is equal to 5 instead of 6 as for Λ →∞. A similar phenomenon

can be observed qualitatively for grains with n>6, however, quantitatively

it manifests itself as less pronounced. For example, the line

(n)forn>6

intersects the axis n in the point n =7atΛ=1.11. For rather large Λ both

the lines — for n<6andn>6 — merge, as can be seen for Λ = 10

PROBLEM 4.6

As shown in Chapter 3 for the steady-state motion of a grain boundary half-

loop the following relations for the grain boundary velocity and the velocity

of the facet hold:

V =

γ(θ − ϕ)

a/2 −  sin θ

(8.215)

636 8Solutions

FIGURE 8.10

Diagram “grain area change vs. topological class” for diﬀerent values of the

criterion Λ.

V =

γ sin ϕ sin θ



(8.216)

In the case that the grain boundary system includes a triple junction

(Fig. 8.11) the velocity of the triple junction can be expressed as

V = m

(2γ cos ϕ cos θ − γ) (8.217)

It is stressed that for a steady-state motion the faceted and the curved

segments of the half-loop along with the triple junction have to move with the

same velocity.

Combining Eqs. (8.215) and (8.216) yields the length of a moving facet

 =

a/2

sin θ +

(θ−ϕ)

sinϕ·sinθ

(8.218)

From Eqs. (8.215) and (8.217) we arrive at



−  sin θ



θ − ϕ

2cosϕ cos θ −1

(8.219)

One can see that the left hand-side of Eq. (8.219) constitutes the criterion

Λ for a grain boundary system with triple junction and a facet. However,

8Solutions 637

FIGURE 8.11

Grain boundary system with facets and triple junction.

contrary to the criterion Λ considered in Chapter 4, there is one distinctive

property of the criterion analyzed here. Namely, since the right-hand side of

Eq. (8.219) is a constant value, by deﬁnition, the changes in grain boundary

and triple junction mobility have to be compensated by a variation of the

facet length .

If the ratio

increases  tends to its maximal value  =

2sinθ

.By

contrast, when the decrease of the ratio

causes the disappearance of the

facet  = 0, the grain boundary system transforms into the well-known grain

boundary conﬁguration with a triple junction (Fig. 4.2). Indeed, in this case

ϕ = 0 and Eq. (8.219) converts to

2θ

2cosθ − 1

(8.220)

Combining Eqs. (8.216) and (8.217) we arrive at



sin ϕ sin θ

2cosϕ cos θ −1

(8.221)

Again, as discussed above, the left-hand side of relation (8.221) is a criterion

Λ for a grain boundary half-loop with facet and triple junction; this criterion

is expressed in terms of triple junction and facet mobility. Contrary to the

criterion (8.219), an increase in the ratio

in (8.221) leads to a reduction

of . One can see that at  = 0 the right-hand side tends to zero as well: at

 =0theangleϕ =0.