Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications
Подождите немного. Документ загружается.


7.1 Appendix A 587
The expressions for the fluxes (j
i
= L
ik
X
i
) can be written using the same
restrictions used by Darken (L
11
= L
22
=0,∇n
1
= −∇n
2
, v
1
= v
2
=Ω
a
,
the atomic volume)
j
0
1
= −L
11
kT
n
1
∇n
1
+Ω
a
∇
p
j
0
2
= −L
22
−
kT
n
2
∇n
2
+Ω
a
∇
p
(7.5)
It follows from the constancy of the volume that j
0
1
+ j
0
2
=0sothat
∇p = kT
L
22
n
2
−
L
11
n
1
Ω
a
(L
11
+ L
22
)
∇n
1
(7.6)
Since L
ii
= D
ii
n
i
/(kT), then
∇p =
kT
Ω
a
D
2
− D
1
D
1
n
1
+ D
2
n
2
∇n
1
(7.7)
One can see from (7.7) that the resulting pressure gradient ∇p is propor-
tional to the difference of the diffusion coefficients (mobilities) and disappears
in the absence of a concentration gradient.
For the classical case (the mobility (diffusion coefficient) of one of the com-
ponents is equal to zero) the expression (7.7) reduces to the van’t Hoff equa-
tion.
As shown in [621], the inclusion of the osmotic pressure in the diffusion pro-
cess leads to the same equation (7.2) for the interface (inert markers) velocity,
whereas the expression for the chemical diffusion coefficient, obtained with a
consideration of the osmotic pressure, is essentially different from Darken’s
equation
1
˜
D
=
N
1
D
2
+
N
2
D
1
(7.8)
Actually, Eqs. (7.3) and (7.8) show that under the condition D
1
D
2
(N
1
∼
=
N
2
) the velocity of mixing in Darken’s theory is determined by the
diffusion of the “fast” component (
˜
D
∼
=
N
2
D
1
) whereas in the “osmotic” the-
ory it is controlled by the diffusion of the “slow” component, which is more
reasonable from a physical point of view. In some cases the relation (7.8) gives
a better agreement with experiment than (7.3).
© 2010 by Taylor and Francis Group, LLC

588 7 Appendices
7.2 Appendix B
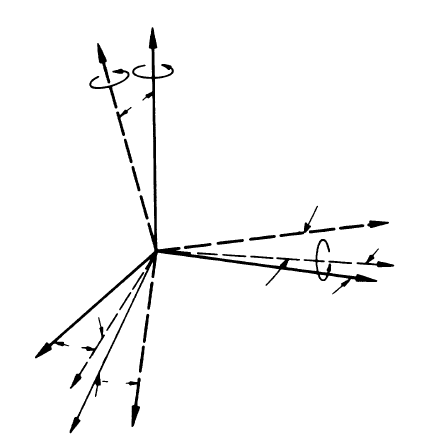
7.2.1 Calculation of the Rotation Matrix
(a) Euler angles: g (ϕ
1
, Φ,ϕ
2
)
If 2 coordinate systems {K
1
} and {K
2
} are given, the rotation of {K
1
} into
{K
2
} can be described in terms of three successive rotations about base vec-
tors of the coordinate systems according to Euler. This procedure defines the
three Euler angles ϕ
1
, Φ,ϕ
2
(Fig. 7.1).
• ϕ
1
(rotation g
1
):
rotate {K
1
} about z
1
by ϕ
1
, so that rotated x (i.e. x
1
) lies in plane
(x
1
, x
2
,). The rotated system is termed {K
1
} = {x
1
, y
1
, z
1
} with
z
1
= z
1
.
• Φ (rotation g
2
):
rotate {K
1
} about x
1
by Φ so that the rotated z
1
(i.e. z
1
) is parallel to
z
2
. The two times rotated systems is termed {K
1
} = {x
1
, y
1
, z
} with
x
1
≡ x
1
and z
2
≡ z
2
.
• ϕ
2
(rotation g
3
):
final rotation of {K
1
} about z
1
≡ z
2
by ϕ
2
so that the rotated x
1
and
y
1
(i.e. x
1
, y
1
) coincide with x
2
and y
2
, respectively.
Now all rotated base vectors of {K
1
} coincide with the base vectors of {K
2
}
and the rotation is complete. In terms of the cube axes {[100], [010], [001]}
and for rolling geometry with rolling direction RD, rolling plane normal ND
and transverse direction TD, the coordinate systems read:
{K
1
} = {RD, TD, ND}
{K
1
} = {RD
, TD
, ND}
{K
1
} = {RD
, TD
, [001]}
{K
2
} = {[100], [010], [001]}
Making use of the rule that the rotation matrix for two subsequent rotations is
given by the product of the matrices for each rotation, we obtain the rotation
matrix for the Euler rotation g(ϕ
1
, Φ,ϕ
2
)
g = g
3
· g
2
· g
1
(7.9)
© 2010 by Taylor and Francis Group, LLC
7.2 Appendix B 589
010
TD’
TD
001
100
ND
RD”
RD’
φ
ϕ
1
ϕ
2
ϕ
2
φ
ϕ
1
ϕ
1
ϕ
2
φ
RD
FIGURE 7.1
Definition of Euler angles.
The rotation g
1
is about base vectors ND and thus easy to put up (note:
right-hand convention) with
x
1
=
⎛
⎝
cos ϕ
1
sin ϕ
1
0
⎞
⎠
y
1
=
⎛
⎝
−sin ϕ
1
cos ϕ
1
0
⎞
⎠
z
1
=
⎛
⎝
0
0
1
⎞
⎠
(7.10)
g
1
=
⎛
⎝
cos ϕ
1
−sin ϕ
1
0
sin ϕ
1
cos ϕ
1
0
001
⎞
⎠
(7.11)
Note that the column vectors of the rotation matrix are the base vectors of
the rotated coordinate system with respect to the unrotated system. Since a
rotation is an orthonormal transformation g
−1
= g
. Hence the row vectors of
the rotation matrix are the base vectors of the unrotated system with respect
to the rotated system.
In analogy one obtains the rotation matrices g
2
and g
3
g
2
=
⎛
⎝
10 0
0cosΦ−sin Φ
0sinΦ cosΦ
⎞
⎠
g
3
=
⎛
⎝
cos Φ
2
−sin Φ
2
0
sin Φ
2
cos Φ
2
0
001
⎞
⎠
(7.12)
© 2010 by Taylor and Francis Group, LLC

590 7 Appendices
[hkl]
[uvw]
RD II x
2
ND II z
2
9
FIGURE 7.2
Definition of Miller indices.
which gives g according to Eq. (7.12) as
g=
2
6
6
4
cos ϕ
1
cos ϕ
2
−sin ϕ
1
sin ϕ
2
cos φ sin ϕ
1
cos ϕ
2
+cos ϕ
1
sin ϕ
2
cos φ sin ϕ
2
sin φ
−cos ϕ
1
sin ϕ
2
−sin ϕ
1
cos ϕ
2
cos φ −sin ϕ
1
sin ϕ
2
+cos ϕ
1
cos ϕ
2
cos φ cos ϕ
2
sin φ
sin ϕ
1
sin φ −cos ϕ
1
sin φ cos φ
3
7
7
5
(7.13)
This is the rotation matrix expressed in terms of the Euler angles.
The representation (hkl)[uvw] and ω[hkl] are readily related to this rotation
matrix.
(b) Miller Indices: g(hkl)[uvw]
Let [uvw] be a vector of {K
1
} that is parallel to x
2
(of {K
2
}) and [hkl] a vector
of {K
1
} parallel to z
2
(of {K
2
}). Since the column vectors of g are identical
with the rotated base vectors of {K
1
}, the rotation matrix must read
g =
⎡
⎣
u
N
1
vl−kw
N
3
h
N
2
v
N
1
hw−ul
N
3
k
N
2
w
N
1
uk−vh
N
3
l
N
2
⎤
⎦
(7.14)
with
N
1
=
!
u
2
+ v
2
+ w
2
N
2
=
!
h
2
+ k
2
+ l
2
N
3
= N
1
· N
2
By means of Eq. (7.14) [uvw] and (hkl) can be determined from g and vice
versa. An example is the representation of an orientation in a rolled sample
with respect to the rolling plane (hkl) and rolling direction [uvw] (Fig. 7.2).
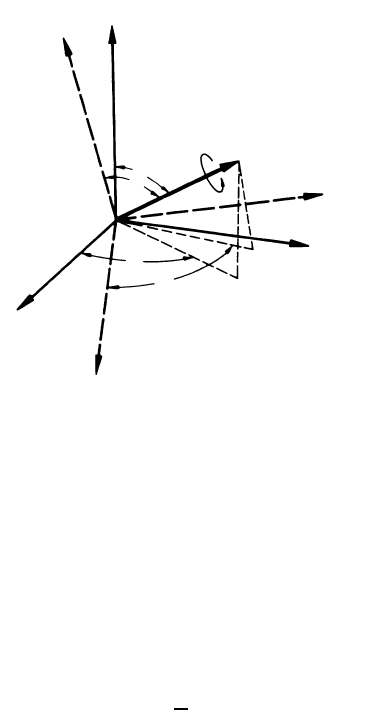
(c) Axis and angle of rotation: g(ω[HKL])
The most imaginative description of a rotation is the notation in terms of angle
and axis of rotation. It can be derived by rotating {K
1
} = {(100), (010), (001)}
and {K
2
}={RD, TD, ND} into an intermediate coordinate system {K
i
} with
the z
i
axis parallel to the rotation axis r. The rotation is then completed by
a rotation of {K
i
} about z
i
with angle ω (Fig. 7.3).
© 2010 by Taylor and Francis Group, LLC
7.2 Appendix B 591
RD
ND
001
010
100
TD
ϑ
ω
ψ
ψ
r II z
i
FIGURE 7.3
Definition of Miller indices.
The rotation axis is by definition common to both, the rotated and un-
rotated coordinate system. Thus, it has the same vector components with
respect to both lattices. Defining the rotation axis in polar coordinates Ψ and
ϑ we obtain a simple relation between axis and angle of rotation and to the
Euler angles.
In order to rotate z
1
into r around RD by ϑ,itmustbe
ϕ
1
= ψ +
π
2
, Φ=ϑ (7.15)
with respect to the Euler angles. Since in the intermediate system only the z
axis is defined to be parallel to r,thex and y axes are arbitrary. For conve-
nience they are chosen such that the rotation of the system {K
2
} coincides
with the intermediate system after (ϕ
1
, Φ, 0). Correspondingly the system
{K
1
} has to be rotated by ϕ
1
, Φ,ω.Weobtain
{K
i
} = g
1
(ϕ
1
, Φ,ω) {K
1
}
{K
i
} = g
2
(ϕ
1
, Φ, 0) {K
2
} (7.16)
{K
2
} = g
−1
2
(ϕ
1
, Φ, 0) · g
1
(ϕ
1
, Φ,ω) {K
1
}
and the components of the rotation axis r =(a
1
,a
2
,a
3
)
a
1
=sinϑ cos ψ; a
2
=sinϑ sin ψ; a
1
=cosϑ (7.17)
© 2010 by Taylor and Francis Group, LLC

592 7 Appendices
The rotation matrix in terms of axis and angle of rotation reads:
g=g
−1
2
(ϕ
1
,Φ,0)·g
1
(ϕ
1
,Φ,ω)=
=
⎡
⎣
(
1−a
2
1
)
cos ω+a
2
1
a
1
a
2
(1−cos ω)+a
3
sin ωa
1
a
3
(1−cos ω)−a
2
sin ω
a
1
a
2
(1−cos ω)−a
3
sin ω
(
1−a
2
2
)
cos ω+a
2
2
a
2
a
3
(1−cos ω)+a
1
sin ω
a
1
a
3
(1−cos ω)+a
2
sin ωa
2
a
3
(1−cos ω)−a
1
sin ω
(
1−a
2
3
)
cos ω+a
2
3
⎤
⎦
(7.18)
With the notation
g =
⎡
⎣
g
11
g
12
g
13
g
21
g
22
g
33
g
31
g
32
g
33
⎤
⎦
(7.19)
the following relations are obtained
a
1
· 2sinω = g
23
− g
32
(7.20a)
a
2
· 2sinω = g
31
− g
13
a
3
· 2sinω = g
12
− g
21
and
ω =arccos
1
2
(a
11
+ a
22
+ a
33
− 1)
(7.20b)
Since a
2
1
+ a
2
2
+ a
2
3
= 1, the rotation axis is known from g according to
Eq. (7.20a) with a constant multiplier 2sinω, which is eliminated by nor-
malization.
7.3 Appendix C
7.3.1 Indexing of Pole Figures
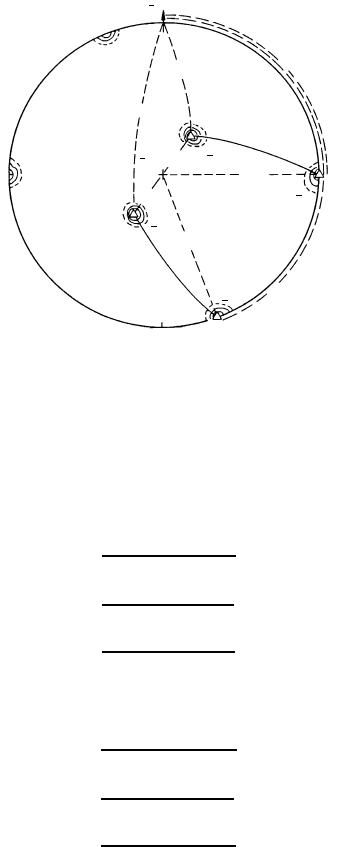
We will demonstrate the procedure to determine the orientation from a pole
figure for the orientation (0
¯
11)[211] (brass orientation in an fcc lattice), which
is supposed to be given in terms of its {111} pole figure (Fig. 7.4). If the ori-
entation of the crystal is determined, the rotation matrix is easily constructed
as shown above. In this case
{hkl} =(0
¯
11)
[uvw]=(
¯
2
¯
1
¯
1) (7.21)
[qrs]=(
¯
111)
© 2010 by Taylor and Francis Group, LLC

7.3 Appendix C 593
and according to Eq. (7.14)
g =
⎛
⎜
⎝
−2
√
6
−1
√
3
0
−1
√
6
1
√
3
−1
√
2
−1
√
6
1
√
3
1
√
2
⎞
⎟
⎠
(7.22)
The Miller indices of the orientation can be found from the pole figure as
follows. Let the specimen axes’ rolling direction (RD), normal direction (ND),
and transverse direction (TD) and the four {111} poles be defined as
a =(a
1
,a
2
,a
3
) = (111)
b =(b
1
,b
2
,b
3
)=(
¯
111)
c =(c
1
,c
2
,c
3
)=(
¯
1
¯
11) (7.23)
d =(d
1
,d
2
,d
3
)=(1
¯
11)
x =(x
1
,x
2
,x
3
)=RD
z =(z
1
,z
2
,z
3
)=ND
The orientations of the vectors a, b, c and d are denoted in the pole figure.
Since the orientation is given by the vectors of the rolling direction RD(=x)
and the rolling plane normal ND(=z) in terms of the Miller indices {hkl}
and uvw of the corresponding directions in the crystal lattice, we have to
determine the vector components of x and z. For the vector z of the rolling
plane normal in the crystal coordinate system the dot products with the four
{111} poles yield
(z, a)=|z|·|a|cos α
z
= z
1
a
1
+ z
2
· a
2
+ z
3
· a
3
(z, b)=|z|·|b|cos β
z
= z
1
b
1
+ z
2
· b
2
+ z
3
· b
3
(7.24)
(z, c)=|z|·|c|cos γ
z
= z
1
c
1
+ z
2
· c
2
+ z
3
· c
3
(z, d)=|z|·|d|cos δ
z
= z
1
d
1
+ z
2
· d
2
+ z
3
· d
3
The angles α
z
through δ
z
can be read from the pole figure by means of
a Wulff’s net. If we choose for simplicity the length of the vector z to be
|z| =1/
√
3, then we obtain from Eq. (7.24) with the vector components for
a, b, c and d according to Eq. (7.23)
cos α
z
=+z
1
+ z
2
+ z
3
cos β
z
= −z
1
+ z
2
+ z
3
(7.25)
cos γ
z
= −z
1
− z
2
+ z
3
cos δ
z
=+z
1
− z
2
+ z
3
© 2010 by Taylor and Francis Group, LLC
594 7 Appendices
x=RD
z
=
ND
ϑ
x
=118°
γ
x
=62°
β
x
=90°
γ
z
=35°
α
z
=90°
α
x
=160°
ϑ
z
=35°
d
a
b
c
β
z
=90°
{111}
FIGURE 7.4
{111} pole figure of single crystal orientation (0
¯
11)[211].
Since the four angles α
z
, β
z
, γ
z
, δ
z
are known, we can calculate the vector
components of z
z
1
=
cos α
z
− cos β
z
2
= h
∗
z
2
=
cos β
z
− cos γ
z
2
= k
∗
(7.26)
z
3
=
cos α
z
+cosγ
z
2
= l
∗
The same procedure holds for the vector x (rolling direction)
x
1
=
cos α
x
− cos β
x
2
= u
∗
x
2
=
cos β
x
− cos γ
x
2
= v
∗
(7.27)
x
3
=
cos α
x
− cos γ
x
2
= w
∗
The vectors (h
∗
,k
∗
,l
∗
)and[u
∗
,v
∗
,w
∗
] thus determined are not yet identical
with the Miller indices {hkl}, [uvw], because of their non-integer components.
One has to multiply these vectors with corresponding factors such that the
vector components become integers. In most cases the vector components are
real numbers and there is no unique factor such as to make all vector compo-
nents integers. Then a compromise has to be found between the accuracy of
the approximation and a low value of the indices. In respective tables Miller
indices are usually restricted to values of 15 or less.
© 2010 by Taylor and Francis Group, LLC

7.3 Appendix C 595
The normalized vectors [u
∗
,v
∗
,w
∗
]/
√
u
∗
+v
∗
+w
∗
and (h
∗
,k
∗
,l
∗
) /
√
h
∗
+k
∗
+l
∗
are identical according to Eq. (7.14) with the first and third
column vectors of the rotation matrix g. The second column is given accord-
ing to Eq. (7.14) by the cross product (z x a). This completely determines
the rotation matrix.
This procedure can be applied to any pole figure {hkl} by associating the
vectors a, b and so on with the respective poles {hkl} and by determining
the dot products of these vectors with x and z according to Eq. (7.25). Of
course, especially simple is the calculation of the orientation from the {100}
pole figure, since the {100} poles represent the projection of the base vectors
of the crystal coordinate system. In this case we obtain
z
1
= h
∗
=cosα
z
x
1
= u
∗
=cosα
x
z
2
= k
∗
=cosβ
z
x
2
= u
∗
=cosβ
x
(7.28)
z
3
= l
∗
=cosγ
z
x
3
= u
∗
=cosγ
x
The Miller indices and the rotation matrix follow in analogy to the example
of the {111} pole figure given above.
Conversely, if the position of a pole in the stereographic projection is to be
determined from a known rotation matrix, this is most conveniently obtained
in terms of the angles α
i
(tilt angle with regard to the rolling plane normal)
and β
i
(rotation in the rolling plane) as depicted in Fig. 7.4. These angles are
related to the vectors of the lattice plane normals N
i
(for instance (1
¯
11) by
means of the rotation matrix
⎛
⎝
sin α
i
cos β
i
sinα
i
sin β
i
cos α
i
⎞
⎠
=
⎛
⎝
g
11
g
21
g
31
g
12
g
22
g
32
g
13
g
23
g
33
⎞
⎠
⎛
⎝
x
∗
i
y
∗
i
z
∗
i
⎞
⎠
= g
−1
· N
∗
i
(7.29)
N
∗
i
=(x
∗
i
, y
∗
i
, z
∗
i
) means the unit vector of N
i
=(x
i
,y
i
,z
i
), i.e. x
∗
i
= x
i
/
!
x
2
i
+ y
2
i
+ z
2
i
. Eq. (7.29) provides another way to determine the Miller in-
dices of an orientation from the measured angles α
i
and β
i
.
When it is possible to evaluate pole figures according to the methods given
above, it is very convenient to utilize tables in which the Miller indices (lim-
ited to values of 15 or less) are listed for all possible angles between related
lattice plane normals and specimen directions [568].
© 2010 by Taylor and Francis Group, LLC

8
Solutions
“You start a question, and it’s like starting a stone.”
— Robert Louis Stevenson
PROBLEM 1.1
It is well known that the principal result of Carnot’s cycle does not depend on
the nature of the “working body” used in the cycle. Let us consider the elemen-
tary Carnot’s cycle which utlilizes a grain boundary as a working body. Let us
consider the diagram surface tension γ vs. area of the surface S (Mlodzeevski,
1939).
In the first stage, we increase the area at constant temperature from S
1
to
S
2
. Due to the constant temperature the surface tension is constant as well.
The formation of a new surface is accompanied by a cooling of the system, so
to maintain a constant temperature the grain boundary should get an amount
of the heat Q = qΔS from the heater; q is the specific heat of grain boundary
area formation.
In the second stage, from point B we increase the grain boundary area
adiabatically. The temperature of the grain boundary drops by dT and the
surface tension γ increases by dγ, respectively.
On the way C-D our grain boundary reduces the area S at constant tem-
perature T −dT . In the course of this process the heat released arrives at the
cooler. Finally, the boundary on the way D-A reduces its area adiabatically.
The work of the cycle is the product
dW =(S
2
− S
1
) dγ (8.1)
The efficiency of the cycle is equal to
η = −
(S
2
− S
1
) dγ
Q
=
dT
T
(8.2)
The “minus” sign indicates that the positive work of grain boundary reduction
is accompanied by the emission of heat; on the other hand, a positive amount
of heat from the heater is absorbed by the grain boundary when it is stretched
by the external forces.
From Eq. (8.2) we arrive at
dγ
dT
= −
Q
(S
2
− S
1
)
·
1
T
(8.3)
597
© 2010 by Taylor and Francis Group, LLC
