Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications
Подождите немного. Документ загружается.


608 8Solutions
That is why the quadruple junction configurations which are observed in 2D
microstructures might be of kinetic origin.
PROBLEM 2.5
(a) Let us consider a grain boundary system which is formed by grain bound-
aries with the surface tensions γ
1
and γ
2
, respectively (Fig. 2.20). The total
free energy of the grain boundaries can be described as
G =
2a
sin α
γ
1
+
a − a
1
tan α
γ
2
(8.50)
The minimum of the Eq. (8.50) is achieved at
cos α =
1
2
γ
2
γ
1
(8.51)
On the other hand, we are looking for the condition when the length of the
cross-piece is equal to zero
= a −
a
tan α
= 0 (8.52)
or tan α =1
α =45
◦
(8.53)
The desired solution is
cos 45
◦
=
1
2
γ
2
γ
1
γ
2
=
√
2γ
1
(8.54)
(b) In accordance with Eq. (8.54) we arrive at the equation
γ
2
(A − lnγ
2
)=
√
2γ
1
(A − lnγ
1
) (8.55)
The solution of Eq. (8.55) is
γ
2
∼
=
0.155 rad or γ
2
∼
=
9.86
◦
(8.56)
(c) The calculation in the frame work of the Read-Shockley equation gives
γ
2
∼
=
17
◦
(8.57)
Strictly speaking, this value is outside the regime of low-angle boundaries. In
other words, we are unable to find a misorientation of the grain boundary
with known surface tension. However, the deviation is rather small, and, for
the first approximation, we can accept this value.
PROBLEM 2.6
(a) Let us consider the merger of two grain boundaries with misorientation
© 2010 by Taylor and Francis Group, LLC
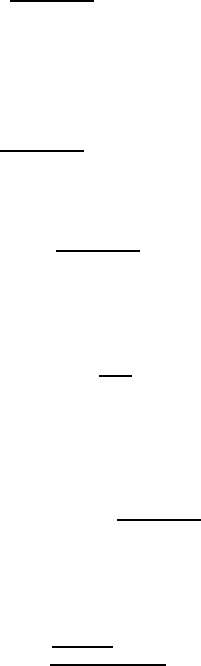
8Solutions 609
angle ϕ
n
.
The surface tension of a low-angle boundary with misorientation ϕ
n
is given
by the Read-Shockley relation (2.3)
γ
n
=
μb
4π(1 − ν)
ϕ
n
[A − lnϕ
n
] (8.58)
After combination instead of two grain boundaries with the energy (surface
tension) given by Eq. (8.58), we will have one grain boundary with misorien-
tation angle 2ϕ
n
with the energy
γ
2n
=
μb
4π(1 − ν)
2ϕ
n
[A − ln 2ϕ
n
] (8.59)
The energy gain is equal to
γ
2n
− 2γ
n
= −
2μb
4π(1 − ν)
2ϕ
n
ln 2 < 0 (8.60)
which is the required result.
(b) The driving force for grain growth can be found from the formal expression
P = −
ΔG
ΔV
(8.61)
where ΔG is the infinitesimal change of the free energy of the system when the
grain boundary sweeps a small volume ΔV . If we displace the grain boundary
by the distance Δx
n
,weobtain
ΔG =(γ
2n
− 2γ
n
) aδ =
−
2μb
4π(1 − ν)
ϕ
n
ln 2
aδ (8.62)
ΔV = aδΔx
n
(8.63)
Then the driving force P reads
P =
2μb
4π(1−ν)
ϕ
n
ln2
Δx
n
(8.64)
(c) The unification of neighboring grain boundaries will be energetically fa-
vorable because this process decreases the stress field of the dislocations. For
angles larger than 15
◦
the dislocation model fails, because the dislocation
cores tend to overlap (see Sec. 2.2.2), and the grain boundary energy remains
essentially constant.
So, with the critical angle taken as 15
◦
we arrive at
ϕ
crit
=15
◦
=0.262 rad (8.65)
On the other hand, the angle ϕ
n
can be defined as
ϕ
n
=2
n
ϕ
0
(8.66)
© 2010 by Taylor and Francis Group, LLC

610 8Solutions
where ϕ
0
is the initial angle of misorientation of two adjacent grains, n is the
number of the step of unification.
The number n can be found from the relation
ϕ
n
=2
n
ϕ
0
= ϕ
crit
(8.67)
and
n =
ln ϕ
crit
− ln ϕ
0
ln 2
(8.68)
For example, if ϕ
0
∼
=
0.001(0.06
◦
) then the number n is equal to
n =
ln0.262 − ln0.001
ln 2
= 8 (8.69)
(d) The grain size Δx
n
at the moment when grain growth will be arrested
can be found from the simple expression
Δx
n
=2
n
Δx
0
(8.70)
If ϕ
0
=0.001 rad and Δx
0
=10
−7
m
Δx
0
=2
8
· 10
−7
m=2.5 · 10
−5
m (8.71)
PROBLEM 2.7
The idea of the solution is that we should compare the energy of a twist grain
boundary with a misorientation angle Δϕ with the elastic energy of a pipe
with a length x
0
, which is twisted by the same angle Δϕ.
The twist angle can be expressed as
Δϕ =
M
k
x
μJ
p
(8.72)
where M
k
is the torque, μ is the shear modulus, J
p
is the moment of inertia.
For a thin-wall pipe (Fig. 2.22)
J
p
=0.5πR
3
δ
The elastic energy of a twisted pipe is equal to
U
el
=
M
2
k
x
2GJ
p
=
Δϕ
2
μJ
p
2x
(8.73)
On the other hand, the energy of a low-angle twist grain boundary with mis-
orientation angle Δϕ reads
γ =
2μb
4π
Δϕ (A − lnΔϕ) (8.74)
© 2010 by Taylor and Francis Group, LLC

8Solutions 611
where b =2.86 · 10
−10
m (for Al) is the Burgers vector, A =0.5 reflects the
energy of the dislocation core.
Since
2πRδγ = U
el
(8.75)
we arrive at
x
0
=
0.5πR
2
Δϕ
b (A − lnΔϕ)
(8.76)
For Δϕ =0.01(∼ 0.5
◦
) we arrive at the surprising result: x = 270m! The
rather strong dependence of x
0
on the radius of the pipe makes the situation
more reasonable for a small pipe diameter. For instance, if R =5· 10
−6
m(5
microns) the length x
0
is equal to ∼ 2.7 mm.
PROBLEM 2.8
The bending stress of a grain boundary as a beam is equal to (Fig. 2.23a)
τ(y)=E
y
ρ
(8.77)
where ρ is the radius of curvature, E is Young’s modulus
1
ρ
=
M
EJ
z
(8.78)
M is the bending moment, I
z
is the moment of inertia of the beam (boundary)
(Fig. 2.23b).
The bending angle ϕ is
dϕ =
Mdx
EJ
z
(8.79)
The free energy of the elastically deformed beam is equal to
G
el
=
−
M
2
dx
2 EJ
z
=
−
M
2
dx
2 EJ
z
=
−
EJ
z
2
1
ρ
2
dx (8.80)
The free energy of the system reads
G =
−
2Δγ
s
y +
EJ
z
2
1
ρ
2
dx (8.81)
The equilibrium shape of the boundary can be extracted from Eq. (8.81),
taking into account that
1
ρ
=
y
(1 + y
2
)
3/2
(8.82)
where y(x) is the equation of the shape of the grain boundary.
The functional of the shape of the grain boundary considered as a beam is
G =
−
2Δγ
s
y +
EJ
z
2
·
y
2
(1 + y
2
)
3
dx (8.83)
© 2010 by Taylor and Francis Group, LLC
612 8Solutions
For small deformation Eq. (8.83) can be transformed to
G
el
=
−
2Δγ
s
y +
EJ
z
2
y
2
dx (8.84)
with the boundary conditions: y(−)=0;y()=0;y
(−)=−tan θ;
y
()=tanθ.
For the sake of simplicity assume that tanθ = 0. The Euler-Poisson equa-
tion, in this case
2Δγ
s
+
d
2
dx
2
EJ
z
2
y
2
= 0 (8.85)
or
y
= −
2Δγ
s
EJ
z
(8.86)
Then we arrive at
y = −
Δγ
s
12 EJ
z
x
4
− 2
2
x
2
+
4
= −
Δγ
s
12 EJ
z
x
2
−
2
2
(8.87)
At x =0y = −
Δγ
s
12 EJ
z
4
.
On the other hand, the grain boundary is curved due to the well-known
balance between the difference of surface tensions of the two grains and the
capillary pressure created by the curved boundary (Fig. 2.23)
2Δγ
s
δ
=
γ
R
(8.88)
In this case the displacement y(0) can be expressed as (Fig. 2.23)
y(0) = R
⎛
⎝
1 −
>
1 −
R
2
⎞
⎠
(8.89)
Eqs. (8.87) and (8.89) define the desired value E as
E = −
Δγ
s
4
12J
z
R
1 −
.
1 −
R
2
(8.90)
where the radius R is defined by Eq. (8.88).
It is noted that the shape of the boundary which is considered as an elas-
tically deformed beam (Eq. (8.87)) and a curved grain boundary (Eq. (8.88))
are different, strictly speaking. However, for our purposes — rough estimation
— such neglect is acceptable. Moreover, as can be seen from Eq. (8.87), for
small x the shape of the loaded beam is a circle.
For Δγ
s
=0.05 J/m
2
, γ =0.5J/m
2
, =0.1cm;R =0.5cm,J =
λδ
3
12
,
where δ is the thickness of the sample (δ
∼
=
10
−2
m), λ is the width of the grain
© 2010 by Taylor and Francis Group, LLC

8Solutions 613
boundary (λ
∼
=
10
−9
m), E
∼
=
0.5 · 10
6
Pa. It should be noted that the elastic
modulus obtained is relevant not only for the grain boundary structure, but
also for the system.
PROBLEM 3.1
Let us consider the behavior of a polycrystal under a hydrostatic pressure
during grain growth. The reduction of the grain boundary area in the course
of grain growth decreases the volume of the specimen and, correspondingly,
decreases the free energy of the system by the value
3pV
ex
<D>
(8.91)
where
3
<D>
is the grain boundary area per unit volume, <D>is the mean
grain diameter, V
ex
is the grain boundary excess free volume and p is the
pressure.
Relation (8.92) can be derived from formal considerations: the pressure
part of grain boundary surface tension is pV
ex
, thus the driving force of grain
growth in a system with mean grain diameter <D>canbeexpressedas
P =
3γ
<D>
+
3pV
ex
<D>
(8.92)
PROBLEM 3.2
First let us calculate the grain boundary mobility under a hydrostatic pressure
m
b
= m
0b
e
−
pV
ex
kT
(8.93)
where m
0
is the grain boundary mobility at the temperature T and the pres-
sure p =0.
Substituting the parameters given in the problem into Eq. (8.93) we get:
m =1.5 · 10
−14
m
4
/Js.
The kinetic equation of grain growth in this case reads
d<D>
dt
=
2m
b
<D>
(γ + pV
ex
) (8.94)
We are interested in the time when grain II disappears, i.e., when grain bound-
ary GB
1
will “meet” grain boundary GB
2
.
From Eq. (8.94) we arrive at
<D
0
>
2
− <D>
2
=4m
b
(γ + pV
ex
) t (8.95)
and, finally
t =
<D
0
>
2
1
− <D
0
>
2
2
4m
b
[V
ex
1
− V
ex
2
]
(8.96)
© 2010 by Taylor and Francis Group, LLC

614 8Solutions
Final result: the time when grain II disappears and the sample will be trans-
formed from a tricrystal to a bicrystal is equal to t = 1333 s.
PROBLEM 3.3
For the motion of spherical boundaries Eq. (8.94) should be changed to
d<D>
dt
=
4m
<D>
(γ + pV
ex
) (8.97)
and Eq. (8.96) will be transformed correspondingly to
t =
<D
0
>
2
1
− <D
2
0
>
2
8m
b
[V
ex
1
− V
ex
2
]
(8.98)
The time t, which defines the disappearance of grain II, will be equal in this
case to
t = 666 s
PROBLEM 3.4
The conditions of thermodynamic equilibrium of a physical body in an exter-
nal field are [5]
T = const. (8.99)
μ = const. (8.100)
Contrary to the temperature and chemical potential the pressure will be dif-
ferent in the different points of the body. In particular, in a gravity field the
potential energy of a molecule u is a function of the coordinates x, y, z of its
center of gravity and does not depend on the disposition of the atoms inside
the molecule
μ = μ
0
+ μ(x, y, z) = const. (8.101)
where μ
0
(P, T ) is the chemical potential in the absence of the field.
The conditions of thermal equilibrium of a body by angular motion can be
obtained by substituting the centrifugal energy as the energy of the external
field u(x, y, z) into Eq. (8.101)
μ
0
(P, T ) −
mω
2
r
2
2
= const. (8.102)
where μ
0
is the chemical potential of the stationary body, m is the mass of
the molecule, r is the distance to the rotation axis.
If we consider the solid or part of the solid so small that it can be described
by the mass M and the radius of angular motion R,thenweget
G = G
0
− Σ
mω
2
r
2
2
= G
0
−
MΩ
2
r
2
2
(8.103)
© 2010 by Taylor and Francis Group, LLC

8Solutions 615
where G
0
is Gibbs’ free energy for a stationary solid.
The density of the grain boundary differs from the density of the bulk of a
grain. Then the driving force of grain boundary motion can be derived from
(8.103) as the difference between the free energy of angular motion of a unit
area of the boundary and the bulk of the same width
ΔG = P =
ρ
bulk
ω
2
R
2
2
−
ρ
bound
ω
2
R
2
2
(8.104)
where ρ
bulk
and ρ
bound
are the densities of the material in the bulk of the grain
and at the grain boundary, respectively. If Γ
0
is the negative autoadsorption,
δ the grain boundary width, and Ω
a
the atomic volume, the desired difference
of the densities in the numerator of (8.104) can be expressed as
ρ
bulk
− ρ
bound
= −
Γ
0
Ω
0
δ
ρ
bulk
(8.105)
Taking Γ
0
= −6.4 ·10
−11
mol/m
2
(see Chapter 1 “Grain boundary excess free
volume”), δ
∼
=
10
−9
m, and the other parameters which are characteristic for
Al, R =0.1m and ω ∼ 2 · 10
3
rad · s
−1
we arrive at
P =
Γ
0
Ω
0
δ
ρ
bulk
·
2 · 10
3
π
2
· R
2
(8.106)
As can be seen the driving force is in the range of 700 J/m
3
=7· 10
−3
MPa,
which is comparable to the capillary driving force of grain boundary motion in
bicrystals. It does no harm that under such driving force the grain boundary
will move to the rotation axis.
PROBLEM 3.5
Let us compare the time necessary to reduce the surface area by the same
value.
For a circle let us determine the time during which the circle disappears,
for the half-loop the time to shorten the area by 2πR.
The solution for the circle is
V = m
b
P =
m
b
γ
R
dR
dt
=
m
b
γ
R
(8.107)
1
2
R
2
= m
b
γt
t =
R
2
2m
b
γ
(8.108)
For the half-loop the expression for the grain boundary velocity reads
V =
πγm
b
R
(8.109)
© 2010 by Taylor and Francis Group, LLC
616 8Solutions
(e)
R
δ
δ
R
(a) (b)
Δ
x
δ
α
Δ
x
α
/2
d
L
A
a
d
δ
(c)
Direction of motion
Δ
x
α
Δ
x
δ
(d)
Δ
x
Δ
x
Δ
x
Direction of motion
(e)
R
δ
δ
R
R
δ
δ
R
R
δ
δ
R
(a) (b)
Δ
x
δ
α
Δ
x
Δ
x
δ
α
Δ
x
α
/2
d
L
A
a
dd
δ
(c)
Direction of motion
Δ
x
α
Δ
x
δ
(c)
Direction of motion
Δ
x
α
Δ
x
δ
Direction of motion
Δ
x
α
Δ
x
δ
(d)
Δ
x
Δ
x
Δ
x
Direction of motion
(d)
Δ
x
Δ
x
Δ
x
Direction of motion
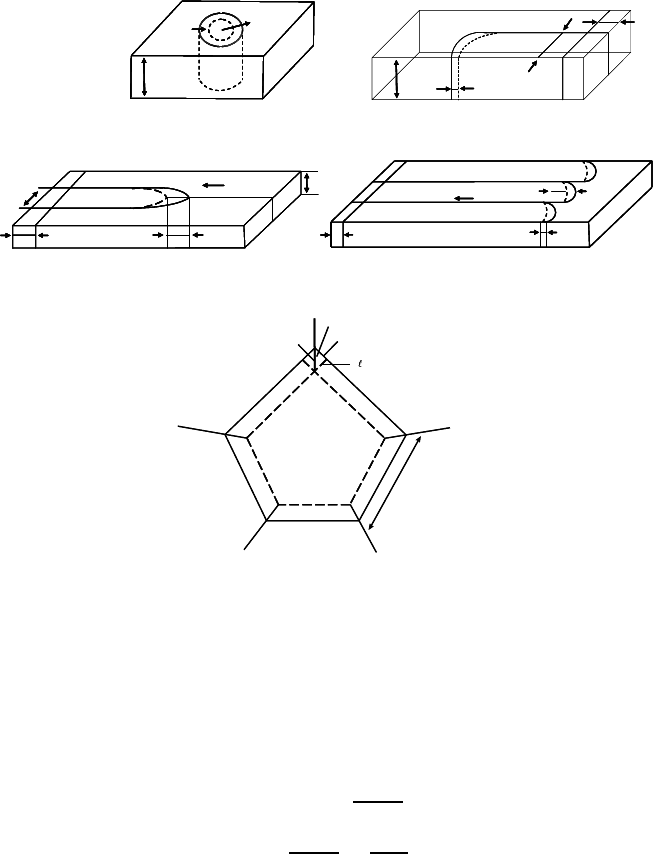
FIGURE 8.5
The diagram shows how to determine the driving force of grain boundary
motion in the “weighted mean curvature” approach for: (a) circular cylinder;
(b) grain boundary quarter-loop; (c) grain boundary system with a triple
junction (n<6); (d) grain boundary system with triple junctions (n>6);
and (e) grain growth of a regular pentagonal grain.
Vt=2πR =
πγm
b
R
t
t =
2πR
2
πγm
b
=
2R
2
γm
b
(8.110)
PROBLEM 3.6
The so-called “weighted mean curvature”-approach (WMC) was introduced
by Herring and Taylor (see Chapter 3). The weighted mean curvature is de-
fined by the reduction of the total interfacial energy (with the sign “-”) in the
course of an infinitesimal displacement divided by the volume swept by this
© 2010 by Taylor and Francis Group, LLC
8Solutions 617
displacement.
1. The driving force for grain boundary motion in a quasi-2D configuration
with circular cylinder can be defined as follows (Fig. 8.5a)
(a) The reduction of the interfacial energy as the result of an infinitesimal
displacement of the grain boundary:
ΔV = d (2πRδγ)=2πδγdR (8.111)
(b) The volume swept by the moving grain boundary:
ΔV =2πRδdR (8.112)
For the driving force we arrive at:
P =
ΔG
ΔV
=
γ
R
(8.113)
2. The driving force for a sphere can be determined in the same way:
P =
ΔG
ΔV
=
8πRγdR
4πR
2
dR
=
2γ
R
(8.114)
3. For the grain boundary quarter-loop (Fig. 8.5b) the change of the interfacial
energy is equal to
ΔG = δΔxγ (8.115)
while the swept volume is equal to
ΔV = δaΔx (8.116)
Then the driving force P is equal to
P =
γ
a
(8.117)
4. 2D uniform (γ
1
= γ
2
= γ) grain boundary system with triple junctions
(1) n<6 (Fig. 8.5c)
(2) n>6 (Fig. 8.5d)
(for the number of the sections N 1).
(1) The reduction of the interfacial energy as a result of an infinitesimal dis-
placement of the grain boundary (Fig. 8.5c) for configuration (c)
ΔG =2γΔx − γΔx = γΔx (8.118)
the swept volume is
ΔV = aΔxδ (8.119)
The driving force is
P =
γ
a
(8.120)
© 2010 by Taylor and Francis Group, LLC
