Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications
Подождите немного. Документ загружается.


618 8Solutions
(2) The reduction of the interfacial energy in the course of a displacement
(Fig. 8.5d):
ΔG = N Δxδγ (8.121)
N is the number of the sections; in Fig. 8.5d three sections are shown.
The swept volume
ΔV = NΔxδaγ (8.122)
The driving force is equal to
P =
γ
a
(8.123)
5. As shown in Chapter 4, in the course of 2D grain growth controlled by
triple junction kinetics a grain of arbitrary shape is bound to transform itself
into an equilateral polygon, and any deviation from an equilateral polygon
will generate a force to restore the equilibrium shape.
Let us consider the evolution of the area and the length of the perimeter of
the n-sided regular polygon in the course of the grain growth at junction ki-
netics in accordance with the “weighted mean curvature” concept. The driving
force P can be expressed as
P =
γ
−2nd
tan
α
2
−1
+ nd
sin
α
2
−1
n · ad
(8.124)
where d is an elementary normal displacement of a grain side, α is the internal
angle of the polygon. The second term in the brackets of the numerator of
(8.124) appears since, in accordance with the WMC, we should take into
account all changes in the course of a small displacement of a facet (side),
including the change of the length of the boundary A in a triple junction
(Fig. 8.5e). The expression (8.124) can be converted to
P =
γ
a
1 − 2sin(π/n)
cos(π/n)
(8.125)
OnecanseethatP varies inversely with the length of the grain side a:for
n<6 the driving force P<0, in other words, such a grain will vanish during
grain growth. For n>6 P>0, such grain will grow, and for n =6,P =0.It
is of interest to know how the driving force P changes with topological class
n. The answer is given by the derivative
dP
dn
dP
dn
=
γ
an
2
2 − sin(π/n)
cos
2
(π/n)
(8.126)
According to Eq. (8.126) the driving force P increases with topological class,
however, the rate of increase slows down with increasing topological class.
PROBLEM 3.7
The derivation of the L¨ucke-Detert relation for grain boundary motion in a
© 2010 by Taylor and Francis Group, LLC
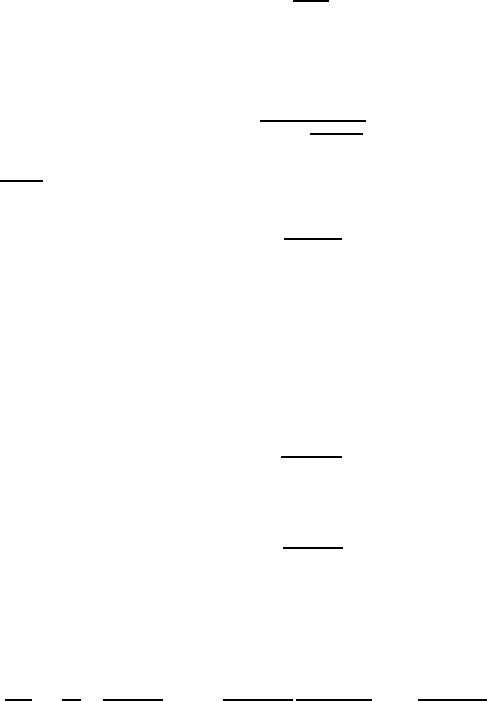
8Solutions 619
system with impurities of positive adsorption is given in Chapter 3.
Let us consider the motion of a flat grain boundary which moves under the
action of a constant driving force P in a system with impurities. The distinc-
tive property of this impurity is its negative adsorption at the grain boundary,
in other words, the concentration of the impurities at the grain boundary is
smaller than in the bulk of the grain. The velocity of grain boundary motion
can be described as
V = P
eff
m
b
(8.127)
The effective driving force P
eff
can be expressed as
P
eff
= P − f Γ (8.128)
where f is a repulsive force between grain boundary and impurity atom, Γ is
the adsorption
f =
V
D
im
(8.129)
where D is the diffusion coefficient of the impurity.
From Eqs. (8.127)–(8.129) we arrive at
V =
Pm
b
1+Γ
m
b
D
im/kT
(8.130)
At Γ
m
b
D/kT
1 we arrive at the L¨ucke-Detert relation
V =
PD
im
Γ kT
(8.131)
We note that the adsorption isotherm in the L¨ucke-Detert relation is the
Henry isotherm: Γ = zBc,wherez is the number of active sites at the grain
boundary, B is the adsorption isotherm.
Let us consider grain growth in a polycrystal with mean grain size <
¯
D>.
The total grain boundary area and the driving force P of grain growth are
equal to
S =
3
<
¯
D>
(8.132a)
and
P =
γ
<
¯
D>
(8.132b)
(The grains are represented by spheres or cubes with diameter or side equal
to <
¯
D>, respectively.)
Then the rate of change of the free energy of the system reads
dG
dt
=
d
dt
3γ
<
¯
D>
= −
3γ
<
¯
D>
2
d<
¯
D>
dt
= −
3γ
<
¯
D>
2
· V (8.133)
© 2010 by Taylor and Francis Group, LLC

620 8Solutions
From (8.130) and (8.133) we arrive at
dG
dt
−
3γ
<
¯
D>
2
·
PD
im
ΓRT
(8.134)
Taking into account that γ = γ
0
+ΓkT (we note that Γ is negative), the
condition of the extremum reads
d
dΓ
dG
dt
=
d
dΓ
−
3
<
¯
D>
3
·
(γ
0
− ΓkT )
2
D
im
Γ kT
= 0 (8.135)
and
−Γ
∗
=
γ
0
kT
(8.136)
As obvious from (8.135) at the point Γ
∗
the derivative
dG
dt
attains a maximum.
Relation (8.136) gives us the adsorption Γ
∗
at which the grain growth in
the system with impurities complies with the maximal rate of free energy re-
duction.
PROBLEM 3.8
The theoretical basis of our current understanding of solute drag is given in
Sec. 3.3.
Here, we give an example of how to apply the theoretical concept to
real experimental data. In our description we will follow the scheme of cal-
culation proposed by L¨ucke and St¨uwe (Chapter 3 [194]) and utilized in
[194, 297, 301, 613]
As the authors of [194] mentioned, they “reformulated and extended the
impurity drag theory in order to simplify the evaluation of measurements.”
That is why we first give a concise approximative approach of the L¨ucke-St¨uwe
theory. In our description we adhere to the designations given in [194], which
will alleviate the utilization of this technique in the future.
The solute drag P
F
(v) exerted on the boundary is equal to
P
F
(v)=N
∞
−∞
c(x, v)
dU
dx
dx (8.137)
where N is the atomic density, c(x, v) is the impurity concentration as a
function of the distance from the grain boundary and the boundary velocity
v,
v = m
b
[P − P
F
(v)] (8.138)
−
dU
dx
is the force exerted by the boundary on a foreign atom. We assume as
the simplest case a triangular potential U(x)ofwidth2a and depth U
0
; U
0
is
the binding energy between boundary and impurity atom (Fig. 8.6).
For this potential Eq. (8.137) reduces to
P
F
(v)=N
U
0
a
0
−a
cdx −
a
0
cdx
= NU
0
c
eff
(8.139)
© 2010 by Taylor and Francis Group, LLC
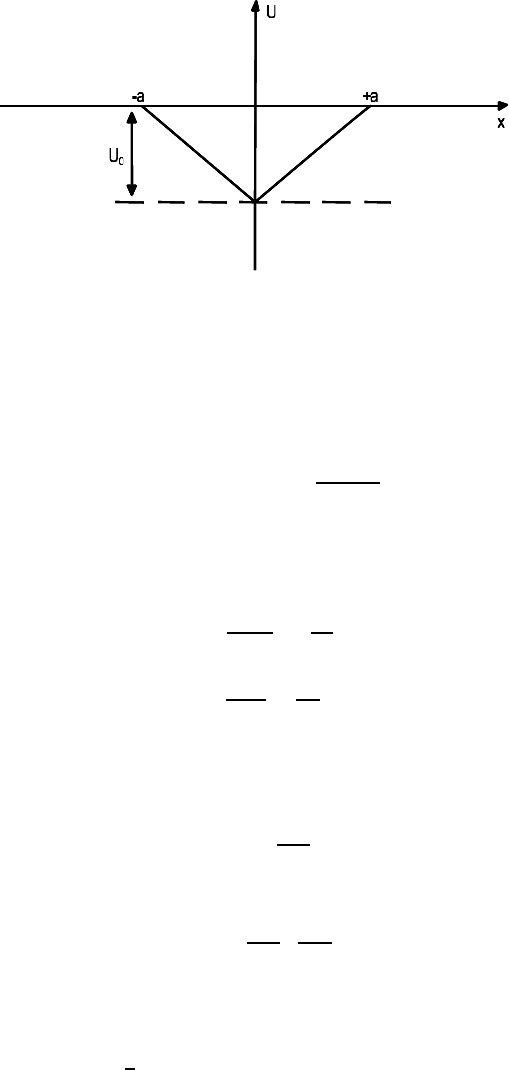
8Solutions 621
FIGURE 8.6
One-atomic boundary. Energy level of an impurity atom in the bulk and in
the boundary.
For quantitative calculations Eq. (8.138) is replaced in [194] by the approxi-
mation
P
F
(v)=NUc
eff
=
rv
1+sv
2
(8.140)
The parameters r and s which do not depend on v are obtained by equating
Eqs. (8.138) and (8.139) for very large and very small v. Then, for D(x)=
D =const and inserting Eq. (8.139) into (8.137) we arrive at the cubic equation
(see Sec. 3.3)
y
3
− y
2
+
1 − ρ
σ
2
y −
1
σ
2
= 0 (8.141)
where
y =
v
A
b
P
=
v
v
F
(8.142)
v
F
is the velocity of a free boundary
v
F
= m
b
P = b
2
PD
m
/kT (8.143)
ρ =2αK
2
D
m
D
c (8.144)
is the reduced concentration,
σ = αK
D
m
D
·
b
3
P
U
0
(8.145)
is the reduced driving force, b is the lattice constant, D = D
0
exp (−Q/kT)
is the diffusion coefficient for atoms lagging behind the grain boundary and
D
m
= D
m
0
exp (−Q
m
/kT) is the diffusion coefficient for matrix atoms cross-
ing the boundary, α =
a
δ
is half of the thickness of the grain boundary, K is
© 2010 by Taylor and Francis Group, LLC
622 8Solutions
a
a
σ
10
10
-1
1
0.1
0.01
10
3
10
2
3.10
-7
10
5
10
4
ρ
10
6
0.1
y=
0.50.97
10
-2
10
-4
10
-3
10
-5
3.10
-2
3.10
-3
3.10
-5
3.10
-4
3.10
-6
1-y=
10
1
10
3
10
2
10
5
10
4
10
6
yy∂∂
==∞
∂σ ∂ρ
a =
a
a
σ
10
10
-1
1
0.1
0.01
10
3
10
2
3.10
-7
10
5
10
4
ρ
10
6
0.1
y=
0.50.97
10
-2
10
-4
10
-3
10
-5
3.10
-2
3.10
-3
3.10
-5
3.10
-4
3.10
-6
1-y=
10
1
10
3
10
2
10
5
10
4
10
6
yy∂∂
==∞
∂σ ∂ρ
a =
FIGURE 8.7
Contour-line representation of the function y = y(σ, ρ), resulting from
Eq. (8.141) [194].
given by
K =
kT
U
0
exp
U
0
kT
− exp
−
U
0
kT
− 2
U
0
kT
1/2
(8.146)
The coefficients in Eq. (8.141) are calculated in the following manner:
1. For the lower part of the curve (Fig. 3.70) it may be assumed that V V
F
and
y =
V
V
F
1
Then
ρ
∼
=
1
y
(8.147)
From the experimental curve (Fig. 3.70) the ratio of the velocities (mobilities)
of “free” and loaded grain boundaries at the temperature of detachment for
curveIIwegetρ = 25.
2. Using the results of a numerical solution of Eq. (8.141) [194] (Fig. 8.7) we
obtain σ = 12.
3. From Eqs. (8.144) and (8.145) we arrive at
2ηK =
Pb
3
ckT
·
ρ
σ
(8.148)
© 2010 by Taylor and Francis Group, LLC

8Solutions 623
2ηK
1
10
2
10
10
4
10
3
10
6
10
5
0
1
10520
15
1
η
η
1
1.5
0
0.5
0.1
0.01
2ηK
2ηK2ηK
1
10
2
10
10
4
10
3
10
6
10
5
0
1
10520
15
1
ηη
ηη
1
1.5
0
0.5
0.1
0.01
2ηK2ηK
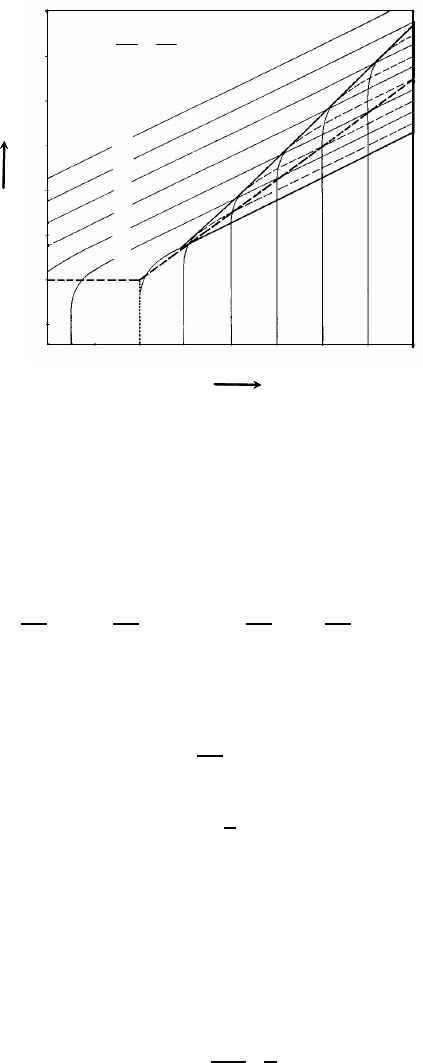
FIGURE 8.8
The function 2ηK (from Eq. (8.146) [194]).
Then, using the dependence 2ηK on η (Fig. 8.8. [194]) and the value of 2ηK
known from Eq. (8.148) we obtain the corresponding value of η
η =
U
0
kT
0
(8.149)
where T
0
is the temperature of detachment.
The determination of 2ηK requires knowledge of the impurities, which are
lost in the course of detachment. As a first approximation let us assume that
this is the impurity with the highest concentration for sample II; this concen-
tration is equal to 3 · 10
−7
.2ηK =8.6,η=2.5,U
0
=0.15 eV, K =1.75.
4. Since the upper branch of the curve (Fig. 3.70, II) characterizes the motion
of a “free” (in the framework of the Cahn-L¨ucke-St¨uwe theory) grain bound-
ary, the parameters of this branch determine the diffusion coefficient of the
matrix atoms in the vicinity of the boundary
D
m
=
V
F
kT
0
P · b
2
=1.7 · 10
−9
m
2
/s (8.150)
The diffusion activation enthalpy of a matrix atom in the vicinity of the bound-
ary [194] can be defined by the grain boundary migration activation enthalpy
E
F
after detachment
E
F
=
∂ ln V
F
∂(1/kT)
= Q
m
− kT
0
(8.151)
Q
m
=0.5eV (8.152)
© 2010 by Taylor and Francis Group, LLC

624 8Solutions
The pre-exponential factor of the matrix diffusion coefficient
D
m
0
= D
m
exp
Q
m
kT
=9.2 ·10
−6
m
2
/s (8.153)
The diffusion coefficient for the impurity atoms can be extracted from
Eq. (8.144)
D =
2αK
2
D
m
ρ
c (8.154)
where α =
a
b
is half of the grain boundary width. For α =1D =1.2 ·
10
−16
m
2
/s, the activation enthalpy of the impurity atoms is equal to
Q = E
L
+ U
0
− 2kT
0
∼
=
0.7ev (8.155)
and the pre-exponential factor D
0
is equal to
D
0
∼
=
10
−11
m
2
/s
Such characteristics of diffusion in an Al matrix are also typical for Fe, Co,
Ni, Mo and Cr. In accordance with the results of the chemical analysis we can
conclude that the most active impurity in our case is iron.
Actually, the diffusion parameters of Fe in Al are D
0
=4· 10
−13
m
2
/s,
Q =0.6eV [622] while the other impurities in Al differ markedly from the
measured values. For instance, for diffusion of Cu in Al D
0
=1.5 · 10
−5
m
2
/s,
Q =1.3eV, for diffusion of Zn along a 38
◦
111 tilt grain boundary in Al
D
0
=1.5 · 10
−3
m
2
/s, Q =0.83eV [280].
The results obtained cause us to reconsider the previous calculation in
the light of the new concentration of the active impurity — the iron atoms:
c =10
−7
.Then2ηK = 26; η =4.0; U
0
=0.25eV, K =3, 25; D =1.4 ·
10
−16
m
2
/s; D
0
=2.5 · 10
−12
m
2
/s.
6. The concentration of the active impurity in the moving grain boundary can
be found from the numerical solution of the differential equation (8.138) as a
function of the reduced velocity: Φ =
Vαb
D
=0.53.
c
eff
c
=2.5
The value of
c
eff
c
makes it possible to determine the drag force P
F
P
F
= NU
0
c
eff
=5.8J/m
2
(8.156)
In the framework of the Cahn-L¨ucke-St¨uwe theories it is assumed that the
grain boundary is homogeneous, in other words, all lattice points in the grain
boundary are potential sites for adsorption of the foreign atoms. However, it
is more likely that the adsorption of impurity atoms occurs on specific active
centers in the grain boundary. The number of such centers can be found
© 2010 by Taylor and Francis Group, LLC

8Solutions 625
10
-1
1
10
3
10
2
10
ρ
1
10
-2
10
-3
10
-5
10
-4
10
-2
10
5
10
10
-1
10
2
10
4
10
3
10
6
η=40
η=20
η=30
η=30
η=10
η=
0
.1
η
=
1
η
=
0
.
3
η
=
3
eff
c
c
10
-1
1
10
3
10
2
10
ρ
1
10
-2
10
-3
10
-5
10
-4
10
-2
10
5
10
10
-1
10
2
10
4
10
3
10
6
η=40
η=20
η=30
η=30
η=10
η=
0
.1
η
=
1
η
=
0
.
3
η
=
3
eff
c
c
eff
c
c
FIGURE 8.9
Effective concentration in the grain boundary as a function of boundary ve-
locity according to continuum theory. Solid lines — Eq. (8.138), dashed lines
— approximation by Eq. (8.139) [194].
© 2010 by Taylor and Francis Group, LLC
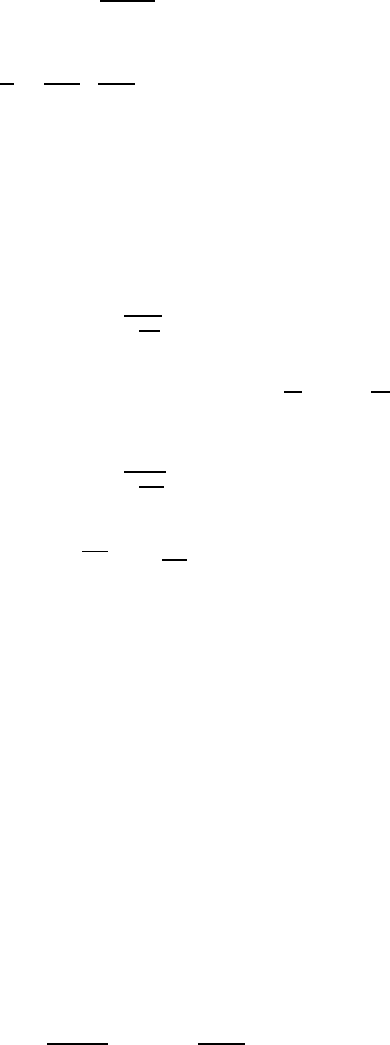
626 8Solutions
from the adsorption isotherm: Γ =
zbc
1−c+bc
(see Chapter 1). For rather small
concentrations the adsorption isotherm can be transformed into Γ = ze
U
0
/kT
c
Γ
c
=
δN
Ω
·
c
eff
c
= z · e
U
0
/kT
(8.157)
where δ is the width of the grain boundary (in [194] δ is assumed to be 2b), Ω
is the atomic volume. Then the number of adsorptionally active sites is equal
to z
∼
=
0.8 · 10
18
m
−2
. The adsorption Γ is equal to Γ
∼
=
5 · 10
12
at/m
2
.
It is useful to compare the results obtained in the framework the Cahn-
L¨ucke-St¨uwe model with the values which can be extracted from the L¨ucke-
Detert approach. In this case the velocity of grain boundary motion is equal
to (Chapter 3)
V =
P
Γ
kT
D
(8.158)
At the detachment of the moving grain boundary from the impurities the
denominator of expression (8.158) can be written as Γ ·
f
0
V
0
,f
0
=
U
0
b
,where
V
0
is the grain boundary velocity at the detachment point. Eq. (8.158) reads
V
0
=
P
Γ
U
0
bV
0
(8.159)
or
ze
U
0
kT
0
· c =
Pb
U
0
(8.160)
Expression (8.160) is an equation with two unknowns: the energy of interac-
tion between impurity atom and grain boundary U
0
and the number of active
sites z. In Fig. 3.70 the results of three independent experiments are presented,
which allows us to determine the desired parameters. The energy of interac-
tion U
0
, defined in the framework of the L¨ucke-Detert mode, is U
0
∼
=
0.5eV;
the number of adsorption sites in the grain boundary z
∼
=
10
14
−10
15
at/m
2
.
The difference between the results obtained in the framework of the Cahn-
L¨ucke-St¨uwe model and the L¨ucke-Detert model becomes apparent if we rec-
ollect the assumptions made in the L¨ucke-Detert approach: all impurity atoms
at the grain boundary interact with the grain boundary with the same force
and, what is important, the grain boundary breaks away simultaneously from
all adsorbed atoms.
PROBLEM 3.9
If the moving grain boundary sweeps all particles in the course of grain growth,
the infinitesimal change of the number n of the particles per unit grain bound-
ary area can be expressed as:
dn =
c
4/3πr
3
4πR
2
dR ·
1
4πR
2
(8.161)
© 2010 by Taylor and Francis Group, LLC

8Solutions 627
where R is the radius of the growing grain.
For the dependence n(R) we arrive at:
n
n
0
dn =
R
R
0
R
4/3πr
3
dR = n−n
0
=
c
4/3πr
3
(R − R
0
) n = n
0
+
c
4/3πr
3
(R − R
0
)
(8.162)
Using the equation for the velocity of grain boundary motion with mobile
particles (Eq. (3.71)), we come to the expression for grain growth kinetics:
dR
dt
=
2m
p
γ
Rn
=
2γm
p
R
n
0
+
c(R−R
0
)
4/3πr
3
(8.163)
Integrating expression (8.163) with regard to (8.162) gives us the desired time
dependency of the radius of the growing grain
2m
p
γt =
R
R
0
R
n
0
+
c (R − R
0
)
4/3πr
3
dR (8.164)
2m
p
γt =
1
3
R
3
− R
3
0
c
4/3πr
3
+
1
2
R
2
− R
2
0
n
0
−
1
2
R
2
R
0
− R
3
0
c
4/3πr
3
Novikov [623] studied the influence of mobile particles, located at a grain
boundary during grain growth. In particular, he discovered that the kinetics
of grain growth, affected by mobile particles can be approximated by the law
R
3
− R
3
0
∼ t.
PROBLEM 3.10
As shown in Chapter 6 the criterion λ
part,b
, which describes the efficiency of
retardation of grain boundary motion by mobile particles reads (see Chapter 3,
Eq. (3.71))
λ
part,b
=
m
p
(r)
n
·
1
m
b
(8.165)
In Eq. (8.165) the simplest case of particle distribution — a single size dis-
tribution — was utilized (see Chapter 3, Eq. (3.71)). The mobility of the
particles m
p
(r) depends on the mechanism of mass transfer during particle
motion and the radius of the particles. n is the number of the particles per
unit of grain boundary area. Let us assume that all particles are located at
the grain boundaries. The number n can be evaluated as the total number of
the particles (c/
4
3
πr
3
) divided by the total area of the grain boundaries per
unit volume (
3
<D>
, <D>is the mean diameter of the grains)
n =
c<D>
4πr
3
(8.166)
The criterion λ
part,b
can be expressed as
λ
part,b
=
m
p
(r) · 4πr
3
c<D>
·
1
m
b
(8.167)
© 2010 by Taylor and Francis Group, LLC
