Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

566 6 Applications

where n (r

) is the number of particles of size r

per unit area.

As discussed in Chapter 3 (see Table 3.2), the particle mobility is deter-

mined by its size and the mass transport mechanism. If mass transport is

conducted through the bulk of a particle m

(r) ∼

;ifitoperatesbyinter-

facial diﬀusion m

(r) ∼

In particular, for rather small particles which are moving by interfacial dif-

fusion (D

), their mobility can be derived as (Table 3.2)

(r)=

πkTr

(6.61)

where Ω

, D

, λ are the atomic volume, interfacial diﬀusion coeﬃcient, and

thickness of the interfacial layer in which the diﬀusion occurs, respectively.

Neglecting the change of grain boundary surface tension due to the depletion

of concentration of the impurity atoms in the bulk of the grains, the condition

for grain growth acceleration can be written (in the case of a uniform size

distribution r = r

) as [607]

< Ω

λ · Γ(c

)

− c

(6.62)

For D

≈ 10

−10

−1

, D

≈ 10

−14

· s

−1

,Ω

∼

−5

· mol

−1

,Γ(c

) ≈

−5

mol · m

−2

, λ ≈ 10

−9

m, c

=1,c

≈ 10

−4

, c

∼

−3

, the particle size

< 10

−6

Grain boundary motion together with the particles is bound to have a

point of detachment. As shown in [607], the detachment condition can be

represented as

f (r

) m

) <V (c

) (6.63)

>λΩ

Γ(c

)

(6.64)

For the values of the parameters given above Eq. (6.64) is followed for

> 10

−15

, for instance, by r

> 10

−7

mand

R<10

−6

Consequently, the predicted eﬀect can actually occur in systems with mo-

bile and immobile particles. From Eqs. (6.55) and (6.56) follows that the eﬀect

in samples with immobile particles is more pronounced in systems with low

solute solubility (c

and c

are small) and rather small mean grain size

R.By

contrast, for mobile particles the only constraint is the size of the particles:

they must be suﬃciently small.

The only experimental data which can be connected with this eﬀect [607]

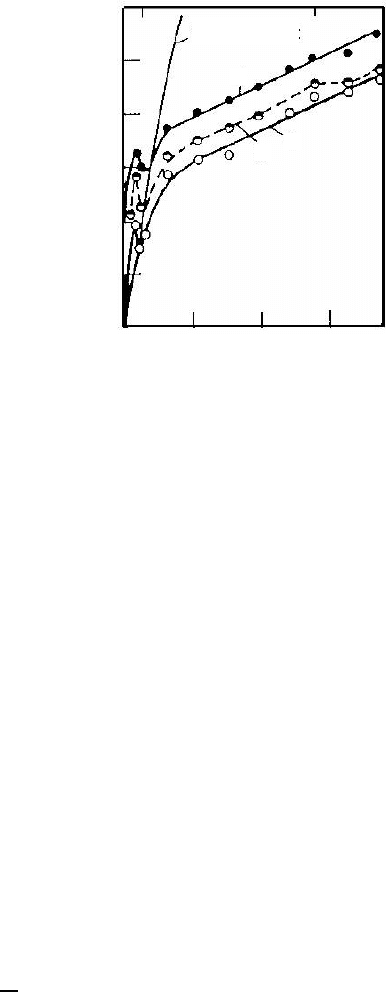
are the recrystallization of Al-Mn alloys [608] (Fig. 6.44). Fig. 6.44 shows the

concentration dependence of recrystallization in Al-Mn alloys for the temper-

ature of diﬀerent stages of recrystallization — the early stage (1 −t

), 50%

recrystallized



2 − t

0.5



and the ﬁnal stage of recrystallization



3 − t



[608]

(Fig. 6.44). In the close vicinity of the solubility limit a sharp minimum can

6.3 On Precipitation-Controlled Grain Size 567

380

220

300

0.0

0.4 0.8

1.2

RX °C

solubility limit

380

220

300

0.0

0.4 0.8

1.2

RX °C

solubility limit

FIGURE 6.44

Concentration dependence of recrystallization temperature T

recr.

of Al-Mn al-

loys with diﬀerent Mn content: 1 — beginning of recrystallization; % recrys-

tallized volume; 2 — 50% recrystallized volume; 3 — terminal recrystallization

[608].

be observed for all t

, indicating an acceleration of the process. It is stressed

that the minimum mentioned is also evident for temperatures at the end of

recrystallization, when the major contribution to the microstructure change is

associated with grain growth, as assumed in the theoretical framework given

above. From the analysis given above it is obvious that the necessary condi-

tions for the eﬀect of precipitation accelerated grain growth are not so tough,

and certainly ought to be observed in nanocrystalline materials.

The approach put forward in [607] was developed in [609]. The main idea

of the proposed approach can be easily understood from consideration of the

simplest case: the behavior of a binary system with a solubility limit c

solute atoms and with zero solubility of the solvent atoms in the pure solute.

The second-phase particles in such a system are particles consisting of pure

solute. For simplicity the density of the solid solution (matrix) and the second-

phase particles is assumed to be equal. The grain boundary is immobile when

the sum of the forces acting on it vanishes

− P

drag

= 0 (6.65)

where P

2γ

is the driving force for grain growth, γ,R are grain boundary

surface tension and radius of curvature, which is proportional to the grain

size D: R = ηD,whereη is in the range of 5 to 10. P

drag

is the drag force

induced by immobile particles, Eq. (6.51). In [609] the situation was considered

568 6 Applications

when the solute atoms are partitioned among the particles, matrix, and grain

boundaries. Both grain boundary adsorption (segregation) and solute drag

are constant since the concentration in the bulk is equal to the solubility

limit during grain growth. However, for rather small particles of radius r the

equilibrium concentration of the second component (impurity) in the bulk

should be diﬀerent from the solubility limit in accordance with the Gibbs-

Thomson relation



= c

exp



2γΩ

rkT



(6.66)



Ω+AΩΓ (c



)+¯c = const (6.67)

where c



is the changed solubility limit, Ω is the atomic volume, Γ (c



), A =

are grain boundary adsorption (segregation) and the grain boundary area per

unit volume of a polycrystal (all grains are supposed to be cuboidal). On the

other hand, the average volume concentration of impurity atoms c,inother

words, the number of the impurity atoms per unit volume of a polycrystal

with mean grain size (radius) D = D

,isequalto

c = c

+ A · Γ(c

)=c

Γ(c

) (6.68)

Therefore

¯c = cΩ − c



Ω − AΩΓ (c



)=c

Ω+

3Ω

Γ(c

) − c



Ω − AΩΓ (c



) (6.69)

Eqs. (6.65) and (6.69) yield the size of the particles which arrest grain growth

in a polycrystal. Eqs. (6.65) and (6.67) allow us to ﬁnd the relation between

grain size and the size of the particles in the form of a diﬀerential equation

[609]. Diﬀerentiation of Eq. (6.69) yields

ηD

−

ηD

2γΩ

exp



2γΩ

rkT



3Ω

Γ(c



)

−

3Ω

dΓ(c



)

(6.70)

where γ is the surface tension of the interface particle-matrix.

Eq. (6.70) predicts an extremum (minimum) of D(r). The integration of

Eq. (6.70) in the limits of D

and D gives the size of the particles which

arrest grain growth in the polycrystal. The equations derived reﬂect the sit-

uation when the particles are located in the bulk of the grains and the grain

boundaries interact with them in the course of grain growth. However, the

conditions of particle formation suggest that there is a large probability for

the scenario that the particles will nucleate directly at grain boundaries. Let

us consider such a situation where all particles are located at grain bound-

aries. In the framework of the Zener approach the drag force of the particles

at grain boundaries is equal to

drag

=2πrγn (6.71)

6.3 On Precipitation-Controlled Grain Size 569

where n is the number of the particles per unit area at the grain boundary,

γ is the grain boundary surface tension. The volume fraction of the particles

canbeexpressedas

¯c = A · n ·

πr

4πn

(6.72)

and

drag

¯cγD

(6.73)

With Eqs.(6.65) and (6.73) we arrive at

2γ

ηD

¯cγD

(6.74)

Eqs. (6.69) and (6.74) yield the size of the particles which arrest grain growth

in a polycrystal for the case when all particles are located at grain boundaries.

The diﬀerential equation, derived in [609], predicts an extremum of D(r),

in analogy to Eq. (6.70). The equations considered are somewhat simpliﬁed.

In the vicinity of c ≈ c

the grain boundaries can be considered as a saturated

by impurity atoms and Γ (c

) = const. For rather “large” particles we can

neglect the Gibbs-Thomson relation. In this case Eq. (6.65) has the solution

r =

ΩΓ (c

) η



D − D



(6.75)

where the initial grain size D

can be extracted from Eq. (6.68)

3Γ (c

)

c − c

(6.76)

When all rather “large” particles are located at the grain boundaries we get

from Eqs. (6.69)) and (6.74)

3Γ (c

)Ω



−



(6.77)

The approach and the equations developed were applied to grain growth in

the system Ni-P studied intensively in [610, 611]. For a polycrystal of Ni with

mean grain size D = 100 nm doped with 3.6% of P the critical (i.e. the max-

imum) radius of the particles which arrests grain growth in such a system is

given in Eq. (6.70): r = η · 2.25 nm and in Eq. (6.77) r =1.6η nm. With

η ≈ 5 the critical particle radius is of the order of 10 nm. We would like to

remind the readers that Eq. (6.70) is derived using the Gibbs-Thomson re-

lation, whereas Eq. (6.77) does not take into account the capillary eﬀect of

small particles.

Up to this point the main goal was to ﬁnd the radius of the particles which

arrest grain growth in the system. This critical radius was treated as a func-

tion of the solute concentration, its limit of solubility, running grain size and

570 6 Applications

grain boundary adsorption. However, the particle pinning of grain boundaries

results from two interdependent processes. On the one hand, solute atoms

are liberated in the course of grain growth, owing to the decrease in grain

boundary area. This gives rise to the nucleation and growth of precipitates.

On the other hand, because particles nucleate and grow, grain growth is hin-

dered and eventually ceases. It is virtually unfeasible to model accurately the

interdependency between grain growth and precipitation. If the bulk solute

concentration corresponds to the solubility limit, grain growth leads to the

formation of precipitates owing to the reduction of grain boundary area. The

concept of grain boundary adsorption in conjunction with particle drag in the

Zener approximation makes it possible to determine both the volume fraction

and the radius of the particles which arrest grain growth.

For a computational exercise an Al-Cu alloy will be considered in the fol-

lowing, with the nominal composition Al-1at%Cu. The initial grain size is set

to D

= 100 nm. The copper adsorption at grain boundaries Γ

is assumed

to be saturated, i.e. 3.2 ·10

−5

mol/m

. These conditions lead to an initial Cu

concentration c

in the grain of 4.5 · 10

mol/m

or 4.4 · 10

−2

at% which cor-

responds to the solubility limit of copper in aluminium at T = 200

◦

Cwhere

tempering is performed. To simplify the calculations, it is also assumed that

the precipitates which arrest grain growth are composed of pure copper and

have a spherical shape.

At the beginning of the heat treatment, there are no particles in the sys-

tem, the average grain size is D

, and the concentration in the matrix equals

the solubility limit c

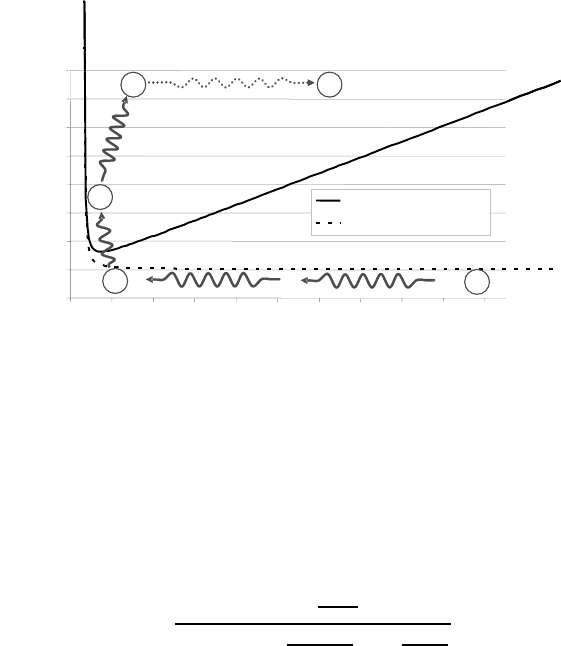
. This state is labeled S in Fig. 6.45. In the ﬁrst stage

of grain growth, all solute liberated from the grain boundaries enriches the

matrix and the solute concentration in the matrix c

rises to

= c

+3Γ







−



(6.78)

As c

increases, the driving force for the phase transformation increases and

the critical radius r

crit

for nucleation shrinks rapidly (dotted line in Fig. 6.45,

[609])

crit

2γV

T · ln





2γV

T · ln



3Γ(c

)



−



(6.79)

where R

is the gas constant.

Eventually a state (N in Fig. 6.45) is reached where nucleation can be

thermally activated. Precipitates are not yet present. The process requires an

incubation period τ

nucl



2 · Z

· β

∗



−1

(6.80)

where Z is the Zeldovich factor and β

∗

the rate at which atoms are added to

the critical nucleus. After incubation the system reaches position I in Fig. 6.45.

At this point, grain boundary pinning can occur. The ﬁrst condition for an

6.3 On Precipitation-Controlled Grain Size 571

0.E+00

1.E-07

2.E-07

3.E-07

4.E-07

5.E-07

6.E-07

7.E-07

8.E-07

Particle radius r in [m]

GrainsizeD in [m]

(D_pin , r_pin) [eq. (21)]

r_crit [eq. (19)]

[Eq. (6.70)]

[Eq. (6.68)]

0.E+00

1.E-07

2.E-07

3.E-07

4.E-07

5.E-07

6.E-07

7.E-07

8.E-07

Particle radius r in [m]

GrainsizeD in [m]

(D_pin , r_pin) [eq. (21)]

r_crit [eq. (19)]

[Eq. (6.70)]

[Eq. (6.68)]

FIGURE 6.45

Pinning of grain boundaries by second-phase particles [609].

eﬀective pining is a state (D, r) above the limit (D

, r

). This limit can be

obtained by integration of the diﬀerential equation (6.70), and is represented

by a solid line in Fig. 6.45 [609]

3Γ (c





1 − exp



2γV

T ·r



3Γ(c

)

(6.81)

The second necessary condition is the precipitation of a suﬃciently large vol-

ume fraction. This is achieved at P in Fig. 6.45, where an eﬃcient pinning oc-

curs and grain growth ceases. However, grain growth does not become arrested

because of particle coarsening, and it evolves slowly to a point E, the end of

the heat treatment. In order to illustrate the above methodology, the points

N-I-P were estimated by computer simulation using the precipitation kinetics

model ClaNG. This model is based on the classical nucleation and growth

theory for precipitation. It follows the Kampmann and Wagner methodology

to determine the evolution of the precipitate size distributions. A detailed

description of the simulation tool can be found elsewhere [610]. In order to

simplify the calculation, the parabolic grain growth kinetics D

(t)−D

= A·t,

A is kept constant and set to 5.0 · 10

−15

−1

(see Chapter 3) are consid-

ered to remain constant with time, i.e. not inﬂuenced by solute content or

precipitate volume fraction, until it ﬁnally ceases. Using the ClaNG model, it

is found that the point N in Fig. 6.45 is obtained very quickly, in less than 1 s.

The ﬁrst precipitates appear after about 20 s when the grain size has reached

D ≈ 300 nm. After 50 s (D ≈ 500 nm), which corresponds to the calculated

572 6 Applications

0.E+00

5.E-08

1.E-07

2.E-07

3.E-07

4.E-07

5.E-07

Particle radius r in [m]

Grain size D in [m]

prec. at grain boundaries

prec. in bulk

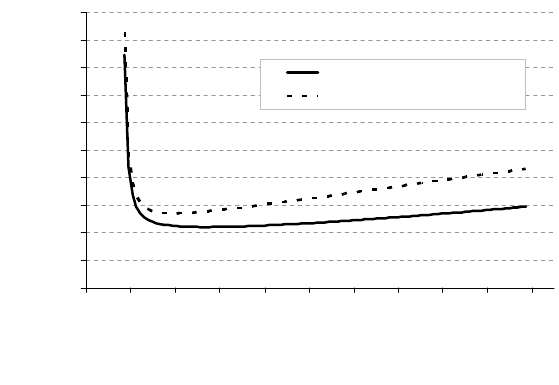
FIGURE 6.46

Pinning region (D

, r

) in case of preferred precipitation at grain bound-

ary. The dotted line indicates the case of homogeneous nucleation in the bulk

[609].

incubation period τ

nucl

, a high density of particles, 10

−3

is present but

the precipitated volume fraction ¯c =2.2 · 10

−7

is still too low to allow an

eﬃcient pinning of the grain boundaries. The critical condition P

drag

= P

is ﬁnally achieved after 150 s. At this time the precipitate density reached

4.3 ·10

−3

for an average radius of 0.8 nm. The grains have grown to their

ﬁnal size D

crit

=0.9 μm and are eﬃciently pinned by second-phase particles.

It is emphasized that the simulations are based on several strong assump-

tions (spherical shape, constant grain growth kinetic) and thus will not repre-

sent a real case, but they render important information on the interplay of the

various concurrent atomistic processes. For instance, it can be learned that

the incubation period τ

nucl

plays an important role [609]. This also holds for a

scenario where pinning originates from particles heterogeneously precipitated

at grain boundaries. In such case the pinning region (D

) is also larger

(Fig. 6.46).

A sensitive parameter is, of course, the initial grain size since it controls

both the amount of liberated solute and the driving force for grain growth

(Fig. 6.47). The interaction of grain growth and precipitation is most eﬀective

for small grain sizes, in particular for nanocrystalline material. If the initial

grain size is changed from D

= 100 nm to D

= 50 nm grain growth will

cease after 43 s at a ﬁnal grain size of D

=0.5 μm and a precipitate size of

=1.4nm(¯c = 0.45%) compared to 150 s, D

=0.9 μm, r

=0.8nm,

6.4 Mechanisms on Retardation of Grain Growth 573

0.0

1.0

2.0

3.0

4.0

5.0

6.0

7.0

0.00.10.20.30.40.50.6

[ m]

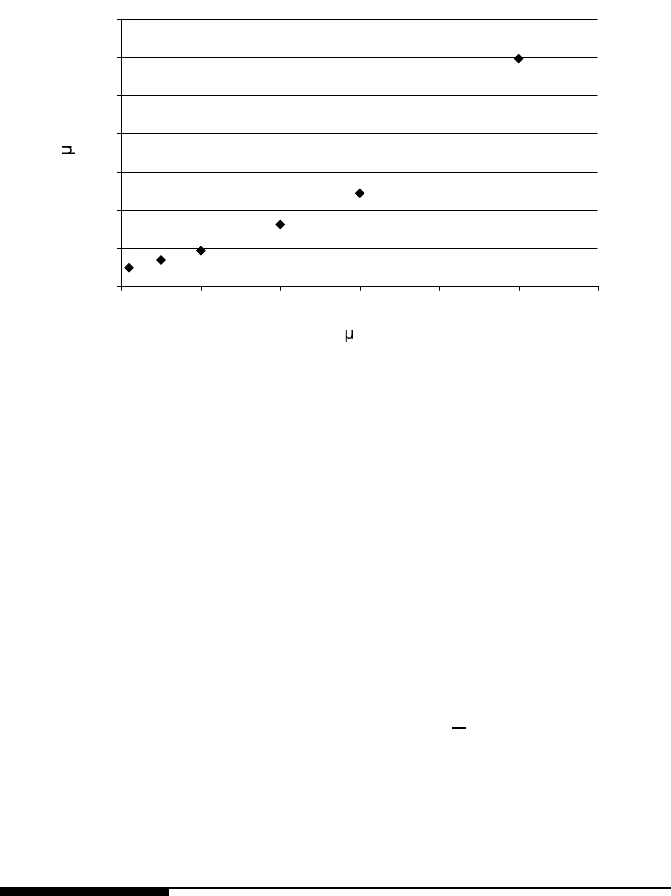
FIGURE 6.47

Dependency of the pinned grain size D

on the initial grain sized D

[609].

f =0.1%.ForD

= 700 nm grain growth would not be arrested even after 10

hours. Therefore, for conventional material with a typical grain size of 10 μm,

a stagnation of grain growth will not be obtained by a redistribution of solute

from boundaries to the bulk.

In spite of several strong assumptions made in the course of the calcu-

lations (spherical shape of the particles, constant grain growth kinetic, the

neglecting of the change of the volume by vanishing grain boundaries: in the

relations discussed the strict Gibbs approach was used, i.e. the volume of the

grain boundaries is neglected; since the volume fraction S/V of grain bound-

aries changes in proportion to 1/D such approximation is reasonable when

D ≥ 50 nm because for cuboidal grain shape S/V=

δ which amounts to 6%

for D = 50 nm and a boundary thickness of 1 nm) computer simulations re-

veal that the respective precipitation kinetics that eventually terminate grain

growth sensitively depend on solute supersaturation and solute diﬀusivity.

6.4 Mechanisms on Retardation of Grain Growth

The design of materials with given requirements for microstructure stability is

connected inseparably with an essential engineering problem: a comparison of

the eﬃciency of the various drag eﬀects on grain growth. Actually, to produce

a ﬁne-grained or nanocrystalline material is part of the problem only. It is of

equal importance to slow down the process of grain growth since the small

574 6 Applications

grain size generates a large driving force for grain growth. In [612] an attempt

is undertaken to assess the eﬃciency of drag eﬀects by diﬀerent structural

elements of a polycrystal on grain growth. The rate of grain area change is

chosen as a measure of stability of a grain structure and the inhibition of

grain growth is pairwise evaluated among all drag eﬀects considered. The

rate of grain area change dS/dt is chosen as a measure for the stability of

a 2D grain structure. The change of grain area characterizes grain growth

to a greater extent than the change of grain size and both can be distinctly

diﬀerent even for the same grain. The consideration of the problem is restricted

by 2D polycrystalline structures. The concepts of grain growth on the basis of

boundary and junction migration best for 2D systems were elaborated. Since

the issue considered is the relative eﬃciency for grain growth retardation a

2D approach is physically adequate. To deﬁne the relative eﬃciency of grain

growth drag due to diﬀerent drag eﬀects the authors of [612] construct a

hierarchy of pairwise dimensionless criteria λ

i,k









(6.82)

which constitutes the ratio of the rate of grain area change for a pair of diﬀer-

ent drag mechanisms. When λ

i,k

< 1 grain growth is controlled by mechanism

(i), and the magnitude of λ

i,k

< 1 denotes the drag eﬃciency.

The rate of grain area change

is expressed by the Von Neumann-Mullins

relation (4.55). The inﬂuence of impurities is reﬂected basically by the grain

boundary mobility m

(c), where c is the concentration of the impurities. The

criterion λ

imp,0

in this case is equal to

imp,0





imp





c=0

(c)γπ

(n − 6)

γπ

(n − 6)

(c)

(6.83)

where





c=0

and





imp

are the rate of grain area change in “pure” metal

and in a metal with impurities, respectively. As the mobility depends strongly

on the crystallographic parameters of a grain boundary the most correct way

to deﬁne λ

imp,0

is to use data for speciﬁc and deﬁned grain boundaries with

diﬀerent amount of impurities. For a 111 tilt grain boundary (misorientation

angle 38.2

◦

(Σ7)) in Al with total impurity content 0.4 ppm and 7.0 ppm,

respectively, at 200

◦

C, λ

imp,0

=5· 10

−4

. For a non-special 111 tilt grain

boundary (misorientation angle 40.5

◦

) at the same temperature λ

imp, 0

1.7 · 10

−4

. The estimation made in [612] for random grain boundary in Al

dopedwithFe(c ≈ 10

−5

) at 200

◦

Cgivesλ

imp,0

≈ 3.6 · 10

−3

The criterion λ for triple junction drag compares the rate of area change

as aﬀected by triple junction with the rate for free uniform boundary motion

6.4 Mechanisms on Retardation of Grain Growth 575

[612]

tj,b

−m

Rnsin



2π



2sin





− 1



γπ

(n − 6)

tj,b

= lim

n→∞









Λ (6.84)

where

R is the grain size, Λ is deﬁned by this equation, n is a topological class

of a grain. A distinctive property of Eq. (6.84) is the explicit dependency of

tj,b

on the grain size. The values of the criterion λ

tj,b

were evaluated in [612]

on the basis of experimental data for a triple junction mobility in pure Al. It

was shown that for Al polycrystal with the grain size

R =10

−8

m at 200

◦

the criterion λ

tj,b

is in the range of λ

tj,b

≈ 10

−12

− 10

−11

To deﬁne the criterion λ

qp,b

, which describes the retardation of grain growth

by quadruple junctions, the approach put forward in [619] can be utilized. As

shown in [447, 619] the grain growth kinetics in polycrystals can be described

by Eq. (4.96)

V =

γκ

where Λ =

and

)

are the criteria which determine the triple

junction drag and the quadruple junction drag of grain growth, respectively.

Then the desired criterion λ

qp,b

can be expressed as a ratio of grain growth

kinetics where the inﬂuence of the junctions is neglected and the grain growth

kinetics inﬂuenced by boundary junction(s)

junctions,b

junctions

(6.85)

Using the value of the quadruple junction mobility in Al evaluated in [447]

(at 600

◦

C m

≈ 2 · 10

−4

−1

) and the experimental data for grain boundary

mobility presented in Chapter 3 for the criterion λ

qp,b

at 600

◦

Cweobtain

qp,b

≈ 10

−13

. The criterion λ

tj,b

at 600

◦

CinAlfor

R ≈ 10

−8

m [436, 437] is

equal to 10

−8

.Atﬁrstglancetheresults(λ

tj,b

 λ

qp,b

) contradict both com-

puter simulation data (see Chapter 4) and our previous calculations. However,

we would like to remind the reader that the latter ones were carried out for

200

◦

C. To recalculate the criterion λ

qo,b

from 600

◦

C to 200

◦

C the quadruple

junction mobility at 200

◦

C should be known. Unfortunately, our knowledge

of quadruple junction mobility is extremely poor. Nevertheless, it can be as-

sumed that the enthalpy of activation of quadruple junction motion is rather

small. It follows both on general grounds (a quadruple junction is a structural

element of zero dimension, similar to a small particle) and the evaluation

of quadruple junction mobility for nanocrystalline Pd at room temperature:

≈ 10

−5

−1

, a value which is very akin to the quadruple junction mo-

bility in nanocrystalline Al at 600

◦

C, in spite of a huge diﬀerence in nature