Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

526 6 Applications

Since the rotation g is deﬁned on a sphere, f(g) can be readily expanded

in terms of the generalized spherical harmonics T

μν

(which are the known

generalized Legendre polynomials)

f(g)=

∞



λ=0



μ=−λ



ν=−λ

μν

(g) (6.21)

Expansion of P

hkl

(α, β) in terms of the reduced spherical harmonics k

(α, β)

yields

hkl

(α, β)=

∞



λ=0



ν=−λ

(hkl)k

(α, β) (6.22)

The correlation between Eq. (6.22) and Eq. (6.21) is given by the integral

equation (5.20) which renders the relation of the coeﬃcients F

and C

μν

(hkl) =

4π

2λ +1



μ=−λ

μν

(α, β) (6.23)

Since T

μν

is known analytically, and C

μν

can be calculated from P

hkl

accord-

ing to Eqs.(6.23) and (6.22) [567], f (g) can be computed from Eq. (6.21). For

practical purposes the expansion has to be limited to ﬁnite values of λ.

Current evaluation programs commonly truncate for λ>22. Taking into

account specimen and crystal symmetry simpliﬁes the procedure for rolled

cubic crystals considerably. In contrast, textures of materials with low crystal

symmetry (most minerals) are not yet analyzed on a sophisticated level.

The computed result for the Cu-rolling texture is shown as an example in

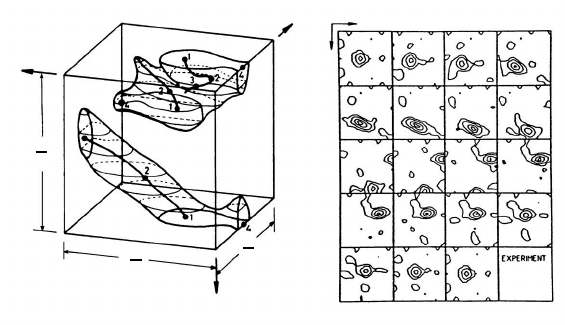
Fig. 6.11. The lines connect points of 1/2 maximum intensity. The texture

resembles a tube in Euler space. The three-dimensional drawing of contour

lines in orientation space is rather inconvenient. Instead, sections parallel to

in increments of Δϕ

◦

are usually presented in the literature.

It is noted again that in highly symmetric lattices like the cubic structure,

the interpretation of the ODF in Euler space is complicated by the presence

of three crystallographically equivalent orientations in the cell 0 ≤ ϕ

, Φ,ϕ

≤

π/2. The appropriate unit cell which accounts for specimen symmetry as well

as crystal symmetry can be of rather complicated shape and, therefore, in-

convenient to handle. Usually, the ODF is represented in 0 ≤ ϕ

, Φ,ϕ

≤ π/2

and the reader has to take note of the multiplicity of symmetric components.

Owing to a long tradition of research on rolling textures in cubic crystals the

most familiar notation of an orientation is still {hkl}uvw. For practical pur-

poses there are conversion tables from {hkl}uvw to (ϕ

, Φ,ϕ

) to facilitate

evaluation.

6.1 Characterization of Microstructure and Texture 527

(a) (b)

FIGURE 6.11

(a) 3D representation of the orientation distribution of rolled high purity

copper in Euler space. Unlike in the 2D pole ﬁgure, here an orientation is

represented unambiguously in three coordinates (by three Euler angles); (b)

Illustration of the orientation distribution by sections through Euler space

perpendicular to the angle ϕ

at 5

◦

intervals.

6.1.3.6 Quantitative Analysis in Terms of Scattered Ideal Orien-

tations

The contour lines of the ODF are rather inconvenient for practical use. Real

textured material contains, however, strong maxima as well as regions with

virtually zero intensity. The maximum intensity can exceed the intensity of a

random distribution (i.e. distribution of a powder specimen) by a factor of 100

and more. The common way of qualitative texture analysis is, therefore, the

interpretation of pole ﬁgures and ODFs in terms of ideal orientations, which

coincide with the dominant maxima in the intensity distribution [572]. When

the intensity maxima are smeared out, there is a certain ambiguity on how

many ideal orientations are necessary to represent the ODF, and what is their

most adequate notation. The Cu-rolling texture is represented in the ODF in

Fig. 6.11 and in the pole ﬁgure in Fig. 6.10. The intensity maxima are well

represented by three ideal orientations which are known under the names:

{011}21

1 brass orientation (main component in brass-rolling texture),

{112}11

1 Cu-orientation (main component in Cu-rolling texture) and

{123}63

4 S-orientation (leads to S-shape of Cu-rolling texture).

For a quantitative texture analysis the scatter σ around the ideal orientation

must be taken into account. For this purpose the ODF is ﬁtted by Gauss-type

528 6 Applications

{111}

= 0°

= 90°

= const.

5° 15°

25°

10°

30°20° 35°

40° 45° 50° 55°

60° 65° 70° 75°

80° 85°

(a) (b)

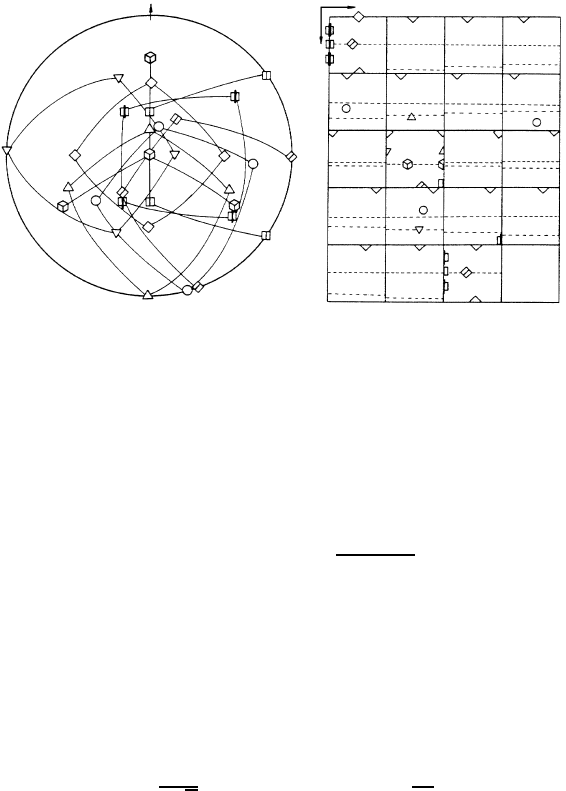
FIGURE 6.12

Main rolling texture components of cubic metals. (a) {111} pole ﬁgure; (b) in

Euler space.

distributions around ideal orientations [573]:

(g)=S

)exp



−

(g − g

)



(6.24)

f (g



(g) (6.25)

From the result the volume fraction M

of each texture component can be

derived by integration of Eq. (6.18) within the orientation regime of each

component and taking note of Eq. (6.19).

√

) σ



1 − exp



−



(6.26)

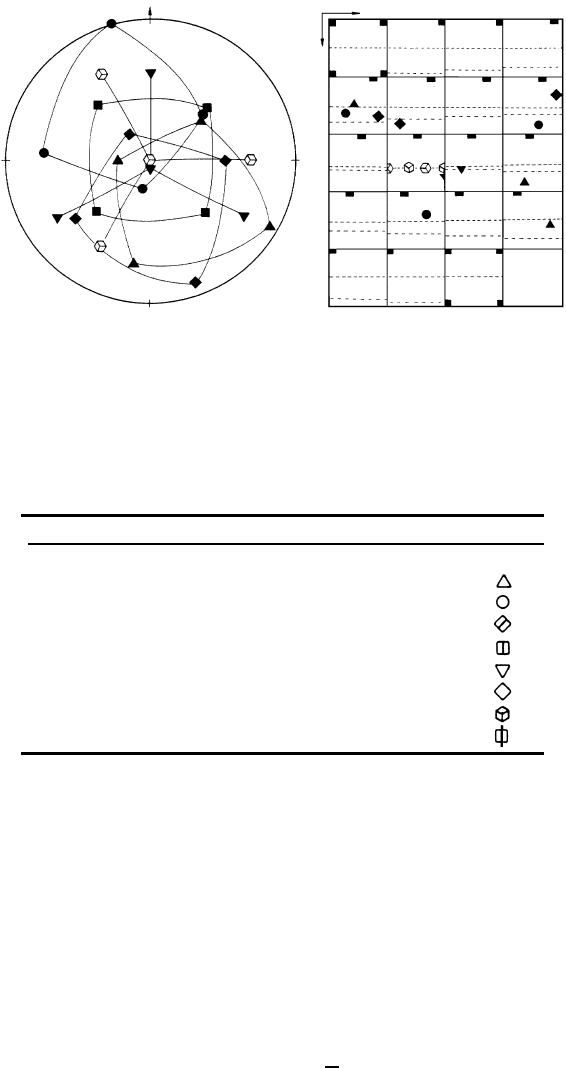
Tables 6.1 and 6.2 and Figs. 6.12 and 6.13 summarize the most important

components of the rolling textures (Fig. 6.12) and recrystallization textures,

(Fig. 6.13) of cubic metals and alloys.

6.1.3.7 Misorientation Distributions

While an orientation represents a rotation of the specimen coordinate sys-

tem into the crystal coordinate system, a misorientation corresponds to the

rotation that makes the two crystal orientations coincide. Therefore, a mis-

orientation distribution can be represented like an orientation distribution, in

6.1 Characterization of Microstructure and Texture 529

{111}

(a) (b)

= 0°

= 90°

= const.

5°

15°

25°

10°

30°20° 35°

40° 45° 50° 55°

60°

65° 70° 75°

80° 85°

FIGURE 6.13

Main recrystallization texture components of cubic metals. (a) {111} pole

ﬁgure; (b) in Euler space.

TABLE 6.1

Main Rolling Texture Components of Cubic Metals

Notation {hkl}uvw ϕ

Φ ϕ

Symbol

C {112}11

1 90

◦

S {123}63

4 59

◦

Bs {011}21

1 35

◦

Goss {011}100 0

◦

{112}110 0

◦

Rotated Cube {001}110 45

◦

{111}11

2 90

◦

Cube

{025}100 0

◦

principle. The most commonly used space to represent an orientation distri-

bution is the Euler space, in particular for the reason that the Euler angles

can be handled as independent and separate variables for the computation

of the ODF. Despite its standard use, Euler space has major disadvantages

owing to its severe distortions, in particular for rotations about the z (ND)

direction.

A representation of misorientation more easy to imagine is the notation

in terms of axis n and angle ω of rotation, which can be most conveniently

represented by its Rodrigues vector [574, 575]

R = n · tan

(6.27)

530 6 Applications

TABLE 6.2

Main Recrystallization Texture Components of Cubic

Metals

Notation {hkl}uvw ϕ

Φ ϕ

Symbol

Cube {001}100 0

◦

R {123}63

4 59

◦

or also {124}21

1 57

◦

bs/R {236}38

5 79

◦

Intermediate {258}1

21 47

◦

{554}22

5 90

◦

{111}11

2 90

◦

{111}1

10 0

◦

in Rodrigues space. The coordinate system of Rodrigues space coincides with

the crystal coordinate system, but its unit cell is determined by crystal sym-

metry. Any misorientation can be represented by its Rodrigues vector R,

which is parallel to the rotation axis n (which, by deﬁnition, is common to

both lattices), and the length of which is determined by tanω/2. This choice

of vector length results in minimal distortions of misorientation space, i.e. all

volume elements are almost equally large, irrespective of their location. In the

following the geometrical properties of Rodrigues space for cubic crystals will

be addressed more closely.

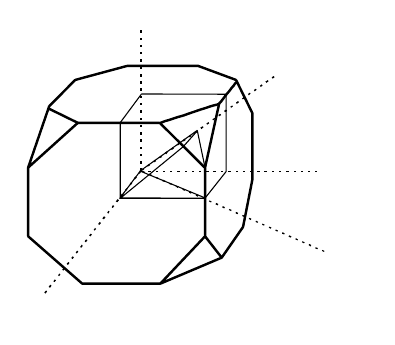
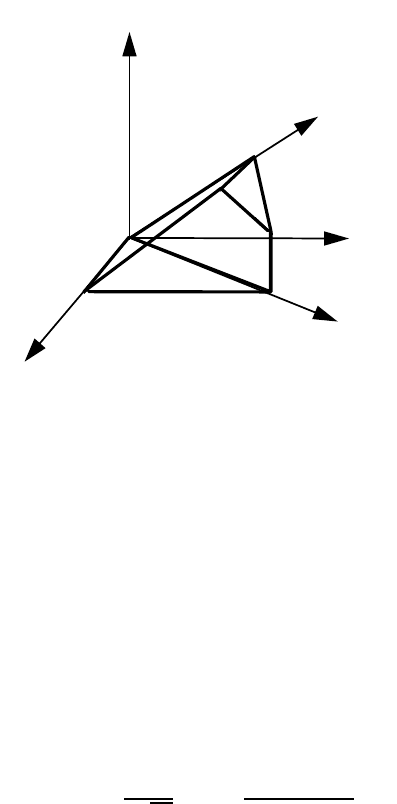
Because of the high symmetry of cubic crystals their fundamental zone in

Rodrigues space is relatively small and simple. Since there are 24 · 24 = 576

diﬀerent ways to represent an orientation relationship in cubic crystals, but

only one is needed, a selection is made with regard to the smallest angle of

rotation to deﬁne the elementary Rodrigues vector. All possible elementary

Rodrigues vectors deﬁne the fundamental zone of Rodrigues space for cubic

crystals (Fig. 6.14). Rodrigues space consists of a cube with the corners cut

oﬀ. The Rodrigues vector emerges from the center of the cube and is deﬁned

by its components with regard to the orthogonal axes, which are parallel to

the cubic crystal axes. The maximum length of a Rodrigues vector along the

100 axes is

√

2−1, corresponding to a 45

◦

rotation. The vector of maximum

length is obtained at the corner of a triangular face. The triangular face is

perpendicular to the 111 axis and intersects the cube at an angle of 60

◦

, i.e.

the center of the triangular face is touched by the Rodrigues vector 1/3111.

The corner of the triangular face corresponds to a 62.8

◦

1, 1, (

√

2 − 1) rota-

tion, which is crystallographically equivalent to a 90

◦

110 rotation. It may

be helpful to remember

• small angle rotations are located close to the origin

•100 rotations extend along the coordinate axes

6.1 Characterization of Microstructure and Texture 531

[010]

[100]

[001]

[111]

[110]

[001]

[111]

[010]

[110]

[100]

FIGURE 6.14

Fundamental zone of Rodrigues space.

•110 rotations extend along the cube face diagonals

•111 rotations extend along the cube space diagonal

• twin rotations (60

◦

< 111) are found in the center of the triangular

faces

If positive and negative rotations about crystallographically equivalent axes

are considered to be equivalent, then the fundamental zone of Rodrigues space

can be reduced to 1/48 of its size, which deﬁnes the so-called Mackenzie cell

(Fig. 6.15). In the Mackenzie cell all equivalent rotations appear only once

[576]. Its shape is odd, however, and therefore less attractive for representa-

tion, since the resemblance to cubic symmetry is less obvious. Therefore, we

prefer to utilize one full eighth of the fundamental zone, which is a capped

cube and thus easy to associate with cubic symmetry. This convenience is

oﬀset by the disadvantage that more than one equivalent rotation will occur

in the chosen subspace. Since the orientation relationships in each square sec-

tion have a mirror symmetry with regard to the diagonal of the square, each

triangle contains three equivalent orientation relationships. This situation is

akin to the representation of orientations in Euler space, where the threefold

111 symmetry also subdivides the cubic 0 ≤ ϕ

, Φ,ϕ

≤ π/2spacewitha

complicated geometry such that one accepts the inconvenience of orientation

532 6 Applications

[01

100

]

[001]

[111]

[11

[100]

[001]

[111]

[010]

[110]

FIGURE 6.15

Mackenzie cell.

multiplicity to maintain the cubic shape of the represented zone.

For a two-dimensional representation equidistant 5

◦

sections through Ro-

drigues space perpendicular to the [001] axis will be used (Fig. 6.16). The

sections also are plotted as complete squares to simplify graphical represen-

tation, although the 111 corner of Rodrigues space is capped. Instead, the

line of intersection with the triangular plane is indicated in the section to de-

note the limit of the fundamental Rodrigues zone. To graphically represent the

misorientation distribution function (MODF) f each measured misorientation

Δg

is associated with a Gauss-type scatter ξ

(Δg

) d (Δg)=

√

2π

exp



−

(Δg − Δg

)

2ξ



d (Δg) (6.28)

f (Δg) dΔg =



(Δg

) d (Δg) (6.29)

and contour lines of equal intensity are plotted. This is entirely analogous

to the representation of the ODF in terms of single grain orientations. For

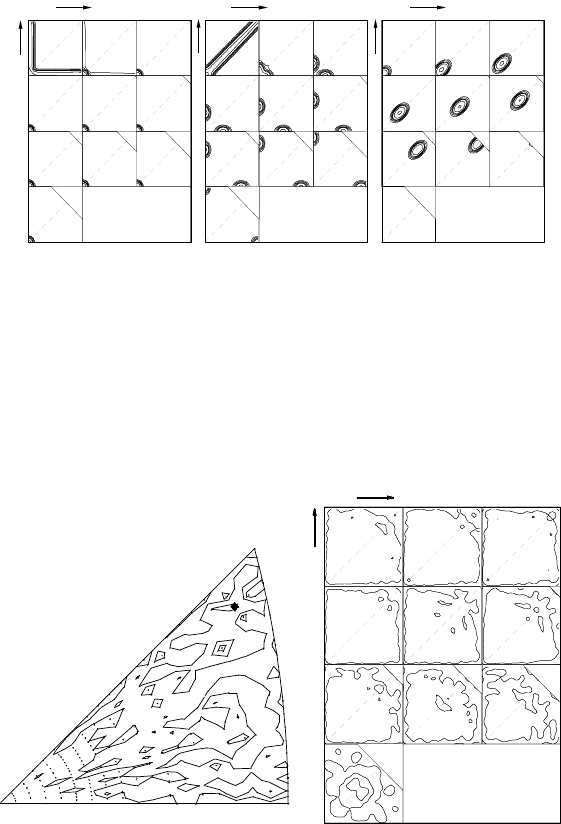
illustration, select misorientation distributions for uniform 100, 110,and

111 rotations are given in Fig. 6.17. We will neglect the (not trivial but not

serious) problem that the scatter of a component can exceed the boundaries

of the Mackenzie cell and, therefore, appears at some diﬀerent location of the

6.1 Characterization of Microstructure and Texture 533

[100]

[010]

[001]

FIGURE 6.16

Equidistant sections through Rodrigues space perpendicular to [001].

cell. As a density function the MODF has to be normalized to unity



f (Δg) d (Δg) = 1 (6.30)

For a particular microtexture, however, it is also important to relate the

measured MODF to a reference MODF [577]. This reference may be either

a random misorientation distribution, which can be calculated analytically

according to Mackenzie, or which can be simulated from a set of random ori-

entations by computing the frequency of occurrence of any misorientation from

the set of misorientations, i.e. the misorientations of each orientation with all

other orientations in the set. If the texture of the specimen is not random,

then the orientation distribution can be discretized and the reference MODF

can be computed analogously. The corresponding misorientation distribution

is also referred to as orientation diﬀerence distribution function (ODDF). The

necessity for this normalization is easy to realize. If a texture would consist of

only two strong components, the probability to measure a misorientation re-

lationship between adjacent grains close to the ideal misorientation of the two

components is much higher than for a random texture. Any deviation from

unity of a MODF/ODDF indicates a nonrandom misorientation distribution.

A random MODF computed for a random orientation set is given in Fig. 6.1.

The MODF normalized by the ODDF is commonly termed orientation cor-

relation function (OCF). For illustration, a microstructure with many small

angle boundaries and ﬁrst order twin boundaries is represented in terms of

MODF, ODDF and OCF in Fig. 6.19.

Every grain boundary manifests a misorientation between adjacent grains,

534 6 Applications

[

]

Probe: 100-Faser

Streubreite: 2°

Levels: 2 4 7 10 20 50

Maximum: 95

Schrittweite: 5° [001]

[

]

Probe: 110-Faser

Streubreite: 2°

Levels: 2 4 7 10 20 50

Maximum: 63

Schrittweite: 5° [001]

[

]

Probe: 111-Faser

Streubreite: 2°

Levels: 2 4 7 10 20 50

Maximum: 59

Schrittweite: 5° [001]

[

]

[

]

[

]

[100] [100][100]

sample: 100-fibre

scatter width: 2°

levels: 2 4 7 10 20 50

maximum: 95

step width: 5° [001]

sample: 110-fibre

scatter width: 2°

levels: 2 4 7 10 20 50

maximum: 63

step width: 5° [001]

sample: 111-fibre

scatter width: 2°

levels: 2 4 7 10 20 50

maximum: 59

step width: 5° [001]

FIGURE 6.17

Representation of orientation relationships in [001] sections of Rodrigues

space: rotations about (a) 100;(b)110;and(c)111 axes.

<100> <110>

<111>

levels

0.50

1.00

2.00

(a)

[

]

[100

]

Probe: Fortunier

Streubreite: 2°

Levels: 0,5 1,0 1,8

Maximum: 1,9

Schrittweite: 5° [001]

[010]

[100]

sample: Fortunier

scatter width: 2°

levels: 0.5; 1.0; 1.8

maximum: 1.9

step width: 5° [001]

(b)

FIGURE 6.18

Random orientation distribution (a) in inverse pole ﬁgure; (b) in Rodrigues

space.

6.2 Recrystallization annd Grain Growth 535

[

]

[

]

[

]

[100] [100] [100]

sample: MODF

scatter width: 2°

levels: 2 4 7 10 20 50

maximum: 85

step width: 5° [001]

sample: OCF

scatter width: 2°

levels: 2 4 7 10

maximum: 15

step width: 5° [001]

sample: ODDF

scatter width: 2°

levels: 2 4 7 10

maximum: 15

step width: 5° [001]

FIGURE 6.19

Comparison of normalization principles (a) MODF; (b) ODDF; (c) OCF.

Small angle relationships (KW), ﬁrst order twin relationships (Z).

by deﬁnition. If the character of a grain boundary can be reduced to its mis-

orientation, i.e. if the spatial orientation of the grain boundary plane can be

neglected, then the distribution of grain boundary character is represented by

the MODF. For a random distribution of all low Σ boundaries with Σ < 29,

where each misorientation was allowed to have a scatter of 5

◦

, the grain bound-

ary character distribution is given in Fig. 6.20.

6.2 Recrystallization annd Grain Growth

6.2.1 Phenomenology and Terminology of Recrystallization

and Grain Growth

The capability of metals to substantially change their properties during a

treatment have made metals and alloys the most versatile and most widely

used structural materials. The macroscopic property changes are mainly due

to either phase transformations or recrystallization and related phenomena.

In this context we will focus on the latter, in particular on recrystallization

and grain growth.

During plastic deformation of a metal due to cold or hot working, disloca-

tions are generated and stored in the crystal. Dislocations are lattice defects,

which do not occur in thermodynamic equilibrium, and, therefore, a deformed

solid tends to remove these lattice defects. On the other hand, although ther-

modynamically unstable, the dislocation arrangement of a deformed crystal