Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

516 6 Applications

(a) (b)

(c)

[hkl]

010

TD’

001

100

001

010

100

RD”

RD’

[uvw]

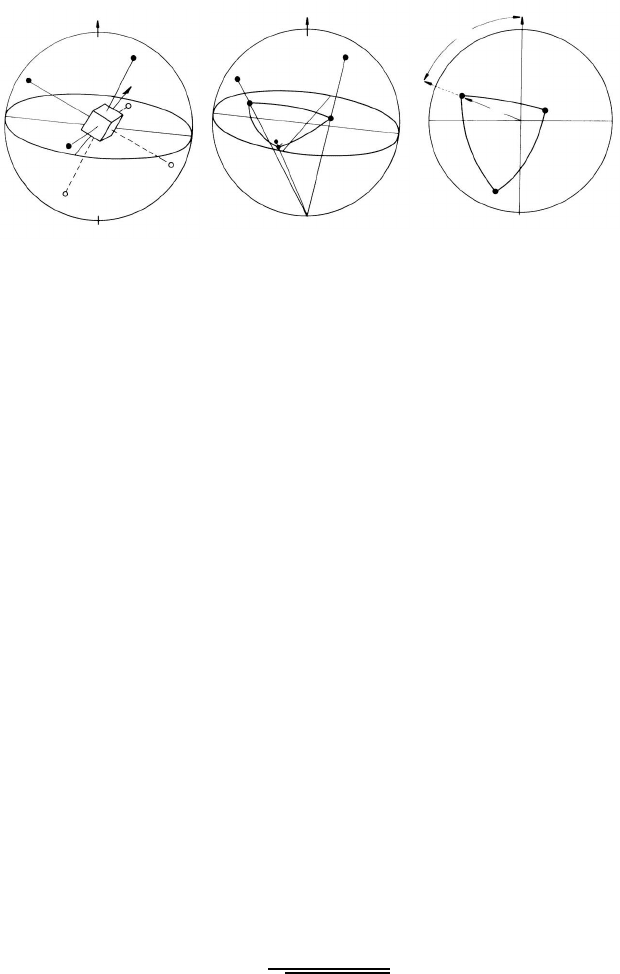
FIGURE 6.4

Diﬀerent representation of an orientation relationship: (a) axis and angle of

rotation; (b) Euler angles; (c) Miller indices.

6.1 Characterization of Microstructure and Texture 517

(i =1, 24). S

is any of the 24 cubic symmetry matrices. In addition there may

be a specimen symmetry, like the orthorhombic specimen symmetry of a rolled

specimen. If the specimen symmetry matrices are denoted by S

(k =1,max),

then





g · (S

)

−1



r (6.12)

6.1.3.2 The Rotation Matrix

Except for the symmetry relations given in Eq. (6.11) the rotation matrix is

unique, irrespective of the way it is derived. It can be expressed in terms of

Euler angles, Miller indices and axis-angle pair as given below. A calculation

of the rotation matrix is given in Appendix B.

g in terms of Euler angles g{(ϕ

, Φ,ϕ

)} is deﬁned as

cos ϕ

−sin ϕ

sin ϕ

cos φ sin ϕ

cos ϕ

+cos ϕ

sin ϕ

cos φ sin ϕ

sin φ

−cos ϕ

sin ϕ

−sin ϕ

cos ϕ

cos φ −sin ϕ

sin ϕ

+cos ϕ

cos ϕ

cos φ cos ϕ

sin φ

sin ϕ

sin φ −cos ϕ

sin φ cos φ

(6.13)

g in terms of Miller indices g{(hkl)[uvw]} is deﬁned as

g =

⎡

⎣

v1−kw

hw−u1

uk−vh

⎤

⎦

(6.14)

where N

√

+ v

+ w

, N

√

+ k

+ l

,andN

= N

· N

;

g in terms of axis and angle of rotation g{ω[a

]} is deﬁned as

(

1−a

)

cos ω+a

(1−cos ω)+a

sin ωa

(1−cos ω)−a

sin ω

(1−cos ω)−a

sin ω

(

1−a

)

cos ω+a

(1−cos ω)+a

sin ω

(1−cos ω)+a

sin ωa

(1−cos ω)−a

sin ω

(

1−a

)

cos ω+a

(6.15)

Since the rotation matrix is unique and independent of its derivation, Euler

angles, Miller indices and axis and angle of rotation can be extracted from a

given rotation matrix with the relations given above.

6.1.3.3 Stereographic Projection, Pole Figure and Inverse Pole

Figure

Orientations are most commonly represented by their pole ﬁgures in the

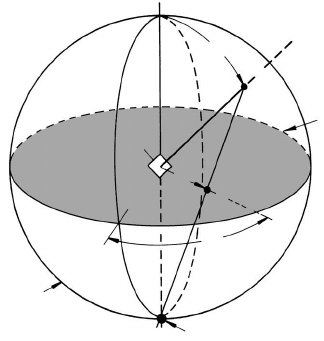
stereographic projection (Fig. 6.5). The stereographic projection is a two-

dimensional image of the three-dimensional orientation space. It is constructed

by placing the origin of the coordinate system in the center of a sphere. A

direction [hkl] (or the normal of a plane (hkl)) centered in the origin will

intersect a surrounding sphere at a point P . The connection of P with the

south pole S of the sphere intersects the equatorial plane at P



. P



is called

the pole of the direction [hkl] (or plane (hkl)). The projection of diﬀerent low

518 6 Applications

reference sphere

center of projection S

equatorial plane =

projection plane

FIGURE 6.5

Illustration of the principle of stereographic projection: E — crystallographic

plane, P



—poleofE in stereographic projection.

index directions with [001] pointing to the north pole of the sphere — which

becomes the center of the projection — is called the (001) or standard pro-

jection.

Limitation to only one set of crystallographically equivalent poles {hkl}

represents the {hkl} pole ﬁgure in standard projection (Fig. 6.6). All other

poles can be constructed by means of the known crystal symmetry. For the

standard projection pole ﬁgures are trivial and superﬂuous. The reference co-

ordinate system, however, is usually the specimen coordinate system {S}.The

orientation of a crystallite with respect to {S} is then denoted by the posi-

tion of its poles within this reference system. This may be illustrated by an

example.

A rolled sample has the distinguished specimen coordinate axes: rolling di-

rection (RD) and rolling plane normal (ND). Consequently, the third orthogo-

nal axis is the transverse direction (TD). The {hkl} pole ﬁgure of a crystallite

is then given by the position of the poles {hkl} within this coordinate system.

The orientation relationship between specimen coordinate system and crys-

tal coordinate system is usually and easily described by the crystallographic

direction parallel to the rolling plane normal (hkl) and the rolling direction

[uvw].

While in normal pole ﬁgures the crystal orientation is represented with

respect to a given specimen coordinate system as a reference, in the inverse

pole ﬁgure the specimen coordinate system is represented with respect to a

given crystal coordinate system (standard position) as a reference (Fig. 6.7).

This is most useful if only one specimen axis is distinguished, like the axis of a

6.1 Characterization of Microstructure and Texture 519

(a) (b)

(c)

ND ND

1' 1'

100

010

001

(a) (b)

(c)

ND ND

1' 1'

100

010

001

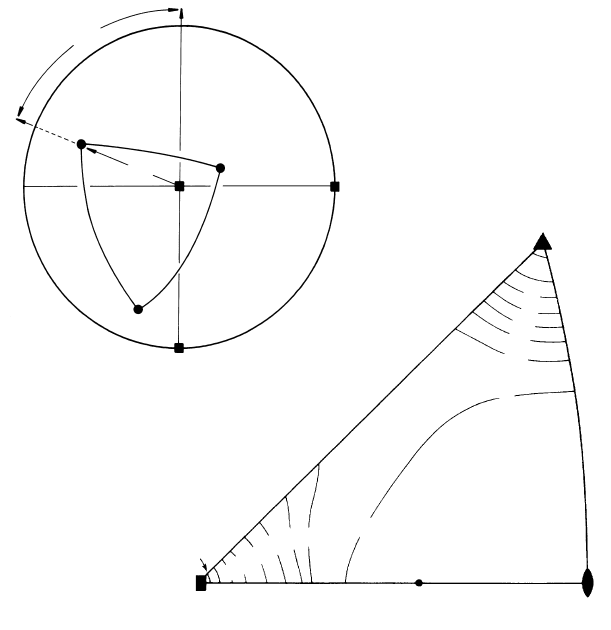
FIGURE 6.6

Representation of an orientation in terms of the {100} axes in stereographic

projection. (a) Position of the crystal at the center of the orientation sphere;

(b) stereographic projection of the cubic axes; (c) {100} pole ﬁgure showing

orientation and deﬁnition of the angles α

and β

associated with pole 1.

wire or a tensile specimen. In cubic crystals the representation can be reduced

to only one characteristic stereographic triangle framed by, e.g. (001)–(011)–

(

111), because of the crystal symmetry.

For more diﬃcult specimen geometries the inverse pole ﬁgure can also be

constructed, but it is less convenient to use, since the whole projection plane

is needed to represent more than one axis in an inverse pole ﬁgure. Therefore,

in such cases, a representation as a pole ﬁgure is more appropriate and easier

to imagine.

6.1.3.4 Measurement and Analysis of Pole Figures

The importance of pole ﬁgures can be attributed to the fact that they can be

experimentally determined with an X-ray texture goniometer. Its principle of

operation is based on Bragg’s law, i.e. the reﬂection of X-rays of wavelength

λ is obtained from a set of planes {hkl} if

λ =2d · sin Θ (6.16)

where Θ is the angle between incident X-ray beam and lattice plane normal

{hkl} (Fig. 6.8). The spacing d between adjacent planes {hkl} in cubic crystals

is given by

d =

√

+ k

+ l

(6.17)

where b denotes the lattice parameter.

The lattice plane normal {hkl} bisects the incident and reﬂected beam at

an angle Θ. For a given wave length λ and for a constant angle 2Θ between

520 6 Applications

(001)

(012) (011)

(b)

(111)

2.5

0.5

22.5

2.5

001

010

100

(a)

FIGURE 6.7

(a) Diagramatic illustration of the inverse pole ﬁgure of a sample of rolled ma-

terial; (b) Inverse pole ﬁgure of extruded aluminum wire (sample orientation

= wire axis). The lines indicate contours of equal measured intensity (after

[569]).

6.1 Characterization of Microstructure and Texture 521

X-ray source and counter a reﬂected signal is counted only if a plane {hkl}

is in reﬂection position. By rotating the specimen around two perpendicular

specimenaxesuptoideally90

◦

all possible positions of planes {hkl} will be

found. Since Bragg’s law does not discriminate signs of {hkl} all combina-

tions of {±h, ±k, ±l} will contribute, i.e. all equivalent poles will be recorded

(Fig. 6.9).

If the specimen is a polycrystal, all crystallites having a set {hkl} in re-

ﬂection position will contribute to the measured intensity for a given position

(α, β) of the specimen. The result of such a measurement is the frequency

of occurrence of a given pole {hkl} in all illuminated crystals for any given

position (α, β) of the specimen, i.e. the pole intensity distribution.

To keep evaluation simple, low index poles like {200}, {220} and {111} for

fcc crystals are usually chosen

The pole ﬁgure represents the distribution of a speciﬁc family of lattice

planes in the stereographic projection. Because of the known crystallography

of the reﬂecting crystal lattice, it is possible to determine the orientation of an

illuminated crystal. To begin with, all poles which belong to the same orienta-

tion, for instance, all four {111} or all three {100} poles have to be identiﬁed.

Since the angles between these crystallographic directions (for instance 90

◦

between any two {100} poles) are known, the orientation can be calculated.

A worked example is given in Appendix C.

In case of single crystals or very simple types of textures (for instance, the

Cube texture) the evaluation of a single pole ﬁgure is suﬃcient to determine

the orientation, since the poles belonging to the same orientation are easy to

identify. However, if several orientations occur concurrently, it is possible that

poles of diﬀerent orientations overlap, which renders impossible an unambigu-

ous association of poles to a deﬁned orientation. In such a case it is necessary

to utilize more than one pole ﬁgure to identify orientations. In experimental

pole ﬁgures of polycrystals, however, an identiﬁcation of all components is

extremely diﬃcult even when several pole ﬁgures are known. In particular,

a quantitative analysis of weaker components is practically impossible. The

fundamental reason for this deﬁciency of a texture analysis by means of pole

ﬁgures is the fact that a pole ﬁgure is a two-dimensional projection (of the

crystal axes) of a three-dimensional quantity (the orientation). This projection

is accompanied by a loss of information, which would be necessary to identify

the poles belonging to a common crystal orientation. However, in the past 20

years mathematical tools have been developed that use high-power computers

to calculate the orientation distribution function (ODF) from a few measured

pole ﬁgures [567]. The result of this computation is not unambiguous. In fact,

it is impossible to determine the true ODF from experimental pole ﬁgures.

This is due to the fact that Bragg’s law does not diﬀerentiate between {hkl}

Because of extinction, in fcc crystals only reﬂection occurs where the Miller indices are

either all even or all odd, i.e. {111}, {200}, .... In bcc crystals, reﬂections only occur if the

sum h + k + l is even, i.e. {110}, {200}, ....

522 6 Applications

wave front

(a)

incident

X-rays

incident

X-rays

incident

X-rays

(b)

(c)

no reflected

X-radiation

(hkl) planes

reflected

X-radiation

reflected

X-radiation

ray 1

ray 2

(hkl) planes

FIGURE 6.8

X-ray diﬀraction by a crystal lattice can be regarded as reﬂection from a semi-

reﬂecting mirror. Only if rays diﬀracted by parallel planes are in phase (b)

(equal phase in every plane perpendicular to the direction of propagation),

they will not cancel each other out (like in (a)) and reﬂection will occur. Equal

phase will result only if the path diﬀerence from successive planes (MPN in

(c)) is an integral number of wave lengths. This condition leads to the Bragg

equation.

6.1 Characterization of Microstructure and Texture 523

(b)

diffractiometer

axis

counting tube

source

(a)

(b)

diffractiometer

axis

counting tube

source

(a)

(b)

diffractiometer

axis

counting tube

source

(a)

FIGURE 6.9

(a) Beam geometry and sample rotation in an X-ray-texture goniometer (here:

the Schulz reﬂection method); (b) X-ray-texture goniometer at the IMM.

524 6 Applications

and {

hkl} poles so that from pole ﬁgures only the symmetrical components

of the ODF can be determined. There are also a variety of methods to deter-

mine the asymmetrical components; however, such solutions are not unique.

Usually the omission of the odd coeﬃcients generates so-called ghosts, that

is, falsely pretended intensities in the ODF, which can be corrected for, if

the major components of the ODF are known. If, however, the true ODF of

an unknown texture ought to be determined, it would be more reasonable to

complement macroscopic pole ﬁgure measurements by single grain orientation

measurements in terms of orientation imaging microscopy (OIM), from which

the true ODF can be calculated, although the number of measured individ-

ual grains may be much smaller than the number of grains contributing to

the intensity in the X-ray pole ﬁgure measurements [570, 571]. It has been

demonstrated recently that, for reasonably deﬁned textures, the true ODF

of a polycrystalline specimen can be calculated with suﬃcient accuracy from

about a thousand randomly sampled individual grain orientation measure-

ments.

6.1.3.5 The Orientation Distribution Function (ODF)

The association of poles belonging to a particular orientation from the in-

tensity distribution in a pole ﬁgure of a polycrystal is usually impossible to

determine. The problem can be alleviated by measuring a second pole ﬁgure

and identifying orientations which comply with both pole ﬁgures. This is very

tedious but it often helps remove ambiguity or rule out the occurrence of a

particular orientation.

A famous example for illustration of this problem is the cube orientation

in the Cu-rolling texture. As will be shown below, a sharp cube texture is

the recrystallization texture of the Cu-type rolling texture. For elucidation

of the texture development it is most important to know whether the cube

orientation is already present in the rolling texture. The {111} pole ﬁgure of

the rolling texture indicates (falsely) that this might be the case (Fig. 6.10).

But the {200} pole ﬁgure of the rolling texture reveals a deﬁnite absence of

the cube orientation (001)[100] in the deformed material, as evident from the

missing intensity in the center of the {200} pole ﬁgure.

In most cases even two pole ﬁgures are not suﬃcient for obtaining an

unambiguous assignment, leaving alone the cumbersome task to compare

the possible orientations. Modern texture analysis instead utilizes the three-

dimensional orientation space. This is the space where any orientation is rep-

resented unambiguously by only one point. Orientation space is set up by

the axes of a three-dimensional coordinate system, where each axis represents

one of the three quantities that deﬁne a given rotation. Correspondingly, the

origin (i.e. no rotation) is the standard orientation (or the orientation of any

given external reference system).

Most common is the rectangular coordinate system with the three Euler

6.1 Characterization of Microstructure and Texture 525

Cu 99.99 {111} Cu 99.99 {200}Cu 99.99 {111} Cu 99.99 {200}

FIGURE 6.10

{111} and {200} pole ﬁgures of 95% rolled Cu.

angles ϕ

, Φ,ϕ

as axes. Any point g



, Φ

,ϕ



in orientation space is

uniquely described by its Euler angles and, therefore, represents exactly the

orientation which is obtained by rotating the standard position (0, 0, 0) by

the angles ϕ

, Φ

,ϕ

. This three-dimensional orientation space is also referred

to as Euler space.

For cubic crystal symmetry and orthorhombic specimen symmetry (like in

rolling) all orientations occur three times in the triple unit cell 0 ≤ ϕ

, Φ.ϕ

≤

π/2 [568]. The function f(g) which describes the frequency of occurrence (in-

tensity) of any particular orientation g in a crystalline aggregate is called the

three-dimensional orientation distribution function (ODF). As pointed out in

Section 5.1.3.1 the value of f(g)foragiveng represents the volume frac-

tion dV/V of material that has an orientation within an inﬁnitesimal volume

around g in orientation space

f(g)dg =

(6.18)

which takes note of the normalization

8π



f(g)dg = 1 (6.19)

where integration is performed over a complete unit cell of the orientation

space.

The measured {hkl} pole ﬁgure P

hkl

gives only the distribution of a par-

ticular crystal axis [hkl]. Every orientation that has an axis [hkl] at a given

point P

in the pole ﬁgure contributes to the intensity at P

. With a point in

the {hkl} pole ﬁgure given by its polar coordinates (α, β) the intensity P

hkl

is given

hkl

(α, β)=

2π



2π

f(α, β, γ)dγ (6.20)