Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

496 5 Computer Simulation of Grain Boundary Motion

still showed some tendency to GB sliding, but its magnitude was far less than

for the Σ5 (36.9

◦

)twistGB.

(d) The ﬁnal displacement ﬁeld found in each (002) plane after a GB had swept

the plane was dominated by in-plane displacements that were linked to the

GB screw dislocation cores. The atoms moved in a cooperative manner. The

largest displacement vectors were in the range of a next neighbor distance or

less. Even at the highest temperatures the discrete screw dislocation network

of the low-angle twist GBs prevailed, and even when the approaching GBs

came very close, this situation did not change. This demonstrates that the

low-angle twist GBs behaved exactly like a discrete screw dislocation network

in fcc crystals. The activation enthalpies found for the low-angle twist GBs

are very low, low even compared to the [001] high-angle twist GBs studied

in this work and must be associated with the motion of the structural screw

dislocations. It also explains the drop in activation enthalpy observed in the

transition from high-angle [001] twist to low-angle twist GBs.

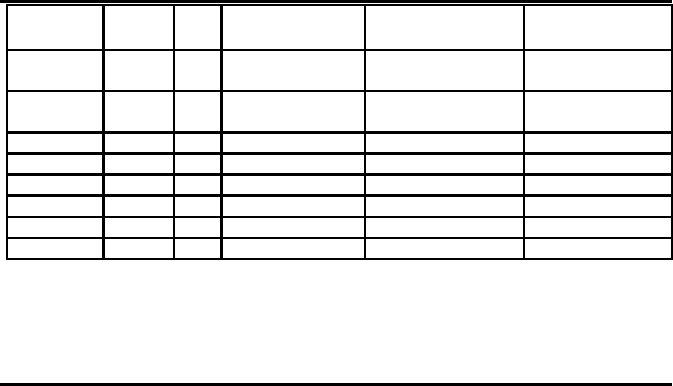
TABLE 5.7

Scaling Behavior of the Found GB Activation Enthalpies of the Studied [001] Twist

GBs for the LJ Potential

GB plane θ Σ Q

GBD

vac

[1] Q

GBM

GBD

[1] Q

GBM

fus

[1]

(001) 43.60

◦

29 0.519 0.428 3.4

43.60

◦

29 0.284 0.404 1.7

(001) 36.87

◦

5 0.528 0.306 2.5

36.87

◦

5 0.347 0.466 —

(001) 28.07

◦

17 0.355 0.381 2.1

(001) 22.62

◦

13 0.414 0.348 2.2

(001) 16.26

◦

25 0.226 0.776 2.7

(001) 12.68

◦

41 0.128 0.433 0.8

(001) 8.80

◦

85 0.297 0.207 0.9

(001) 6.03

◦

181 0.257 — —

Note: Here the activation enthalpy of volume self-diﬀusion via mono-

vacancies in an fcc system modeled by the LJ potential used in this

work with 3D periodic BC is Q

vac

=1.972 eV. Further Q

GBD

represents

the GB self-diﬀusion enthalpy as determined in this work for

each GB and Q

GBM

is the GB migration enthalpy. Finally Q

fus

the latent heat of fusion as determined in [539] and reads Q

fus

=0.13 eV.

5.8.2 Grain Boundary Diﬀusion of [001] Twist Boundaries

Owing to a lack of reliable data on grain boundary mobility it is frequently

assumed that GB migration and GB diﬀusion involve the same mechanisms so

that the activation energies are essentially identical. The computed activation

5.9 Simulation of Triple Junction Motion 497

enthalpies of GB self-diﬀusion of each GB and volume self-diﬀusion are listed

in Table 5.7 namely, r

GBD

vac

GBD

vac

and r

GBM

GBD

GBM

GBD

. These data yield the

following information:

(a) The computed GB self-diﬀusion activation enthalpy for the Σ29 and Σ5

twist GBs in the low temperature regime were about half the value for volume

self-diﬀusion via mono-vacancies. The other listed data in Table 5.7 of r

GBD

vac

range from 0.128 to 0.414 depending on the misorientation angle of the GB.

Generally r

GBD

vac

is assumed to be approximately 0.5.

(b) The r

GBM

GBD

values range from 0.207 to 0.776 depending on the misorienta-

tion angle of the GB. Roughly speaking, the ratio is one third to one half. This

clearly demonstrates that GB migration and GB self-diﬀusion are distinctly

diﬀerent processes. This is supported by the results of the GB migration mech-

anisms; for instance, for high-angle [001] twist GBs a cooperative four atom

shuﬄe mechanism was identiﬁed as the key element which was quite diﬀerent

from the GB diﬀusion mechanism.

This result is also supported by atomic resolution TEM experiments to ob-

serve in situ grain boundary motion [538]. A cooperative shuﬄe process as

the dominant migration mechanism was reported.

5.9 Simulation of Triple Junction Motion

5.9.1 Theoretical Background

In the following we focus on the determination of the intrinsic triple junction

mobilities in simulations where the migration is driven by grain boundary cur-

vature. Two simulation geometries designed to achieve steady-state boundary

and triple junction migration and from which the steady-state triple junc-

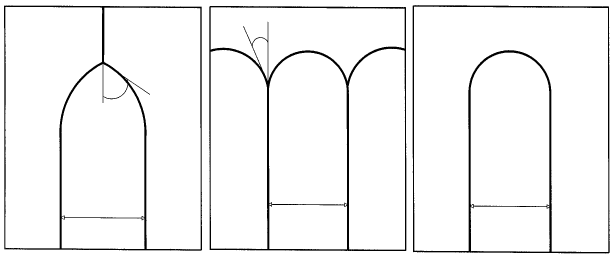
tion mobility may be extracted are shown in Fig. 5.35. In the geometry of

Figs. 5.35(a) and (b), the boundary curvatures are such that the triple junc-

tion moves either into or away from grain a (referred to as the + and –

directions, respectively). Three grains, I, II and III, separated by three grain

boundaries with misorientations αI-II,αI-III and αII-III = αI-II+αI-III meet

at the triple junction. Since the grain boundaries are assumed to extend per-

pendicular to the plane of view, the geometry is quasi two-dimensional. The

II-III grain boundary is assumed to be symmetric such that αI-II = αI-III

and the I-II and I-III boundaries are equivalent. The orientations of the con-

stituent grains in the two geometries are chosen such that the triple junctions

in Figs. 5.35(a) and (b) are structurally identical. The force balance associ-

ated with the grain boundary (surface) tensions (in the direction parallel to

the II-III boundary) at the triple junction results in a thermodynamic driving

498 5 Computer Simulation of Grain Boundary Motion

III

(c)

(a)

(b)

III

(c)

(a)

(b)

FIGURE 5.35

Schematic illustrations of the geometries employed in the simulations. The

deﬁnition of the triple junction angle θ, half-loop grain width a and grain

identities are shown. The orientations of the I, II and III grains are the same

in all three geometries. The misorientation across the I-II and the I-III bound-

aries is ±ϕ and that across the II-III boundary is 2ϕ. The simulation geome-

tries in (a) and (b), referred to as the “+” and “–” geometries because the

II-III boundary increases or decreases, respectively, during curvature-driven

boundary migration. The geometry in (c) represents the simulation cell used

to study boundary migration in the absence of a triple junction; there is a

bicrystal half-loop of width a and area A

[440].

force, F

given by

=2γ

I-II

cos θ

− γ

II-III

= ∓2γ

I-II



cos θ

− cos θ



(5.34)

where the superscript ± indicates that the variable applies to either the “+”

or “–” conﬁguration (Figs. 5.35(a) and (b), respectively), θ is one-half the dy-

namic included angle within grain, I and γ

I-II

and γ

II-III

are the grain boundary

energies (if the boundary energy depends on boundary inclination, then the

boundary energies must be replaced with γ

ηΨ

∂

ηΨ

/∂ϕ

,whereϕ refers to

the orientation of the grain boundary normal and η and Ψ represent either I

or II. In static equilibrium, the net force on the triple junction is zero, F

=0,

such that the static value of θ is given by 2γ cos θ

= γ

II-III

which is used in

the second equality in Eq. 5.34 (γ

is denoted as γ for simplicity). Then the

expression for the triple junction migration rate looks:

= m

= ∓2γm



cos θ

− cos



(5.35)

We can easily extract the triple junction migration rate in terms of a quantity

which can be extracted from the simulations, i.e. the rate of change in area

5.9 Simulation of Triple Junction Motion 499

of the half-loop grain (grain I in Fig. 5.35(a) and grain II in Fig. 5.35(b)).

Geometrically,

is simply the product of the width a of the half-loop grain

and the triple junction velocity, v

= v

a =2γm

a|cos θ

− cos θ

In the simulations, we measure

, θ

and θ

for each set of simulation

conditions (simulation geometry, misorientation ϕ,widtha and temperature

T ) and use the expression for

to extract the reduced mobility of the triple

junction. The normalized triple junction mobility is directly obtainable from

the simulations (

,θ

and θ

)

sim









|cos θ

− cos θ

(5.36)

The mobility ratio Λ

can also be calculated directly from the analytical

result for the triple junction migration given the static and dynamic angles

and θ

= |

cos θ

− cos θ

| (5.37a)

−

= |

ln (sin θ

−

)

cos θ

−

− cos θ

| (5.37b)

Equating the simulation and analytical expressions for the triple junction

velocity gives the relationship between the rate of change in grain area and

the triple junction angles





(5.38a)

and

−

=sin

−1



exp



−



(5.38b)

5.9.2 Simulation Method

Molecular dynamics was performed in the simulations to extract the triple

junction mobility by measuring

pm and the static and dynamic angles θ

and θ

[440]. These quantities were measured as a function of the orientations

of the bounding grains and temperature. The simulations were performed us-

ing the simple, well-characterized Lennard-Jones pair potential. Because the

simulation geometries in Fig. 5.35 are inherently two dimensional, the simu-

lations were performed in two dimensions (i.e. the XY plane). Energies are

reported in units of the Lennard-Jones potential well depth ε,distancein

units of the equilibrium atom separation r

, area in units of the perfect crys-

tal area per atom a

and time in units of τ =(M

/ε)

1/2

,whereM

is the

500 5 Computer Simulation of Grain Boundary Motion

atomic mass. For example, in the case of Al, ε =0.57 eV and r

=2.86

A.The

potential was cut oﬀ at r

=2.1r

, which is midway between the second and

third nearest neighbors in the zero temperature equilibrium triangular lattice.

A velocity-resealing thermostating algorithm was used to set the temperature

[440, 485]. Periodic boundary conditions were employed in the direction per-

pendicular to the straight boundaries in Fig. 5.35. In order to maintain the

grain misorientations (especially at high temperature), the bottom three lay-

ers were frozen. Additionally, the X-coordinates of the atoms in the top three

layers were ﬁxed such that those atoms could move only in the Y-direction to

accommodate the dilatational stresses generated due to the decrease in net

boundary area during the simulation. Additional simulations were performed

in the geometry of Figs. 5.35(a) and (c) with free surfaces on the top and

sides to ensure that these boundary conditions did not signiﬁcantly modify

the results.

The initial atomic conﬁgurations were created by misorienting grains II and

III with respect to grain I by ±ϕ and hence with respect to each other by 2ϕ,

such that the grain boundary II-III is a symmetric boundary. This methodol-

ogy enables the reduction of the description of the entire tri-crystallography

in terms of a single misorientation variable ϕ. The simulation geometries were

relaxed by performing molecular dynamics simulations at very low tempera-

tures (0.0100.025ε/k

) prior to the grain boundary migration study to enable

the atoms at the grain boundaries to equilibrate. The entire system is then

heated slowly to the desired temperature in a step-wise fashion. The migration

rate

is deduced from the slope of the area of the half-loop grain

vs.

time t plot.

is simply the product of the number of atoms in the half-loop

grain and the area per atom a

. This requires the assignment of each atom in

the simulation cell to one of the grains at each time [202]. The dynamic triple

junction angle θ

was extracted by measuring the angle subtended between

the tangent of the I-II grain boundary at the triple junction and the extension

of the II-III boundary into grain I (i.e. θ

I−II

+ θ

I−III

; see Figs. 5.35(a) and

(b)).

and θ

measurements are only made during times for which the grain

boundary(ies) enclosing the half-loop grain shrinks or grows in a steady-state,

self-similar manner. The angles reported were averaged over several measure-

ments during the course of each of three simulations performed for each set

of conditions. The static equilibrium angles θ

were determined by perform-

ing larger scale simulations at high temperatures until the boundaries have

stopped migrating (see [540]).

The dependence of triple junction mobility on grain boundary and triple

junction crystallography is simulated in tri-crystals for a range of boundary

misorientations. Special or singular boundaries (e.g. Σ = 7, θ =38.2

◦

and

Σ = 13, ϕ =32.21

◦

, where Σ is, as usual, the inverse density of coinci-

dence sites), vicinal or near-singular boundaries (near Σ = 7 and Σ = 13),

and general boundaries were all simulated. It should be noted that in the

present 2D triangular lattice simulations, where misorientations correspond

5.9 Simulation of Triple Junction Motion 501

to tilts about the 111 axis in the related fcc lattice, an I-II and I-III

misorientation ϕ corresponding to Σ

I−II

produces a II-III boundary corre-

sponding to Σ

II−III

=Σ

I−II

. All misorientations ϕ were within the range

◦

≤ θ ≤ 40

◦

, where the entire range of unique boundary misorientations lies

between 30

◦

≤ θ ≤ 60

◦

which are symmetry related to those with 30

◦

>θ>0

◦

in this lattice.

Triple junction kinetics were also investigated as a function of grain size

(half-loop width) and temperature. These simulations were performed for tri-

crystallographies for which signiﬁcant triple junction drag was observed. The

simulations were performed for 19r

<w<50r

and 0.075ε/k

<T <

0.250ε/k

. Activation energies for migration were extracted from Arrhenius

plots of the rate of change in half-loop area with temperature. Three runs

were performed for each simulation condition and the simulation parameters.

5.9.3 Simulation Results

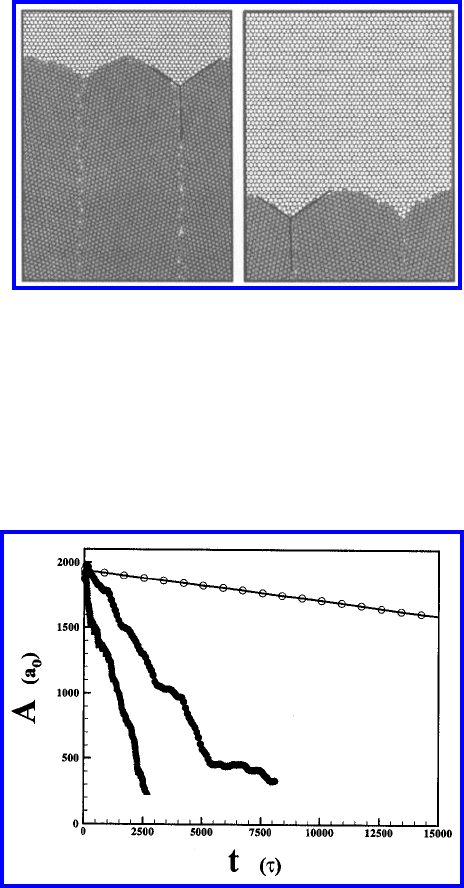
Fig. 5.36 shows the atomic conﬁgurations corresponding to three diﬀerent

times (t = 550τ, 1245τ, and 1750τ), for a simulation performed for the “+”

geometry at T =0.125ε/k

, half-loop width of a =25r

and θ =40

◦

.Careful

examination shows that apart from small ﬂuctuations, the curvatures of the

constituent grain boundaries at the triple junctions remain constant, imply-

ing that the triple junction migration is very nearly self-similar and, hence,

steady state, and that the triple junction angle is preserved throughout the

simulation. Fig. 5.37 shows the atomic conﬁgurations for the simulation ge-

ometry in Fig. 5.35(b) (t = 2000τ and t = 14000τ ) at the same temperature

and half-loop width as in Fig. 5.36. Again, it is clear from the ﬁgure that the

tri-crystal shape is self-similar during its migration.

The self-similarity of triple junction migration enables us to extract the

triple junction migration rate in terms of the rate of change in the area of

the half-loop grain

. The temporal evolution of the grain areas for the

structures in Fig. 5.35 are shown in Fig. 5.38 for the same conditions as in

Figs. 5.36 and 5.37. It is important to note that for the “–” simulation geom-

etry, the total calculated area corresponds to the sum of the areas of grains

I and II, which in turn is twice that of the half-loop area. The half-loop area

decreases with time in a monotonic fashion, with some superimposed noise. At

late times, the retracting half-loop is inﬂuenced by the frozen layer of atoms

at the bottom of the simulation cell and, hence, no measurements can be

made there. Some of the ﬂuctuations seen in Fig. 5.38 at intermediate time

are associated with thermal transients in the shape of the half-loop and triple

junction angle during half-loop retraction.

More detailed discussion of the nature of the ﬂuctuations/transients in the

vs. t plots may be found elsewhere [202]. These transients are excluded

from the determination of the steady-state slope. The regions of steady-state

migration are characterized by constant θ

as well as a linear

vs. t plot.

For the simulation conditions corresponding to Figs. 5.36 and 5.37, the ex-

502 5 Computer Simulation of Grain Boundary Motion

(a)

(b)

(c)

(a)

(b)

(c)

FIGURE 5.36

The atomic conﬁguration of a ϕ =33

◦

migrating triple junction (T =

0.125ε/k

, w =25r

for the “+” simulation geometry at three instants of

time: (a) t = 550τ,(b)t = 1245τ and (c) t = 2550τ. The bold lines indicate

the tangents to the half-loop boundary at the triple junction. The dynamic

triple junction angle was θ

=56

◦

in (a) θ

=58

◦

in (b), and θ

=58

◦

5.9 Simulation of Triple Junction Motion 503

(a) (b)(a) (b)

FIGURE 5.37

The atomic conﬁguration of a ϕ =33

◦

migration triple junction (T =

0.125ϕ/k

, w =25r

) for the “–” simulation geometry, The atomic con-

ﬁgurations correspond to instants of time: (a) t = 2000τ and (b) t = 14000τ .

The dynamic triple junction angle was θ

−

=61

◦

in (a) and θ

−

=62

◦

in (b)

[440].

FIGURE 5.38

The rate of change in the area of the half-loop grain (grain I in Figs. 5.35(a)

and (c), and grain II in Fig. 5.35(b) with and without triple junctions for the

same conditions as in Fig. 5.35(c)). The ﬁlled and open circles indicate the

“+” and “–” geometries, respectively, and the shaded triangles indicate the

results of the bicrystal simulation [440].

504 5 Computer Simulation of Grain Boundary Motion

tracted rates of change of the half-loop grain area are

=0.33 ± 0.06a

/τ

and

−

=0.024 ±0.009a

/τ. The diﬀerence between the two values of

expected based upon the diﬀerences in geometry.

Fig. 5.39 also shows simulation data obtained from the bi-crystal half-loop

(i.e., without a triple junction) simulations (see Fig. 5.35(c), A

vs.t,forthe

same (I-II) misorientation, temperature and half-loop width as for the triple

junction migration simulations. The slope of this curve is

=0.54±0.03a

/τ.

Comparing

and

, it is found that

−

. For the simulations

shown in Figs. 5.36 and 5.37, the average dynamic triple junction angles are

=59

◦

±1

◦

and θ

−

=62

◦

±1

◦

. The static triple junction angle for this tri-

crystallography has been previously determined to be θ

=61

◦

± 1

◦

. Hence,

for this tricrystal, the dynamic triple junction angle θ

is approximately the

same as θ

Figs. 5.40 and 5.41 show the atomic conﬁgurations during triple junction

migration in both the “+” (t = 450τ and (2550τ) and “–” (t = 3000τ and

25000τ) directions, respectively, under the same conditions as Figs. 5.36 and

5.37, but for ϕ =38.2

◦

. This angle corresponds to a high symmetry, low Σ

(i.e., Σ7) misorientation. Once again, it is clear that triple junction migration

takes place in a nearly self-similar fashion, with constant β

. The temporal

evolution of the areas of the half-loop grains for the tri-crystal simulations

shown in Figs. 5.40 and 5.41 as well as the corresponding bicrystal simula-

tions is shown in Fig. 5.42. Averaged over three diﬀerent simulation runs, the

steady-state slopes of the

vs. t plots for the “+” and “–” geometries are

=0.64 ± 0.05a

/τ and

−

=0.039 ± 0.006a

/τ. The rate of change of

area for the bicrystal half-loops at ϕ =38.2

◦

=1.32 ± 0.08a

/τ.The

dynamic triple junction angles for the “+” and “–” geometry are measured to

be θ

=47

◦

±1

◦

and θ

−

=72

◦

±1

◦

, respectively. For this tricrystallography,

the static triple junction angle is θ

=60± 2

◦

. Unlike in the low symmetry

ϕ =40

◦

case, where the triple junction angles were nearly the same in the

“+” and “–” geometries, in the ϕ =38.2

◦

case the triple junction angles are

much diﬀerent (Δϕ =25

◦

± 2

◦

), implying that in the ϕ =38.2

◦

case, triple

junction drag may be substantial.

As mentioned before, one of the major advantages of the computer sim-

ulation approach is the ability to study the eﬀect of grain boundary misori-

entation ϕ on triple junction motion. Triple junction migration simulations

were performed for a total of 13 diﬀerent grain boundary misorientations ϕ at

ﬁxed width (w =25r

) and temperature (T =0.125ε/k

). Depending on the

misorientation,

, and

can be very similar or very diﬀerent (by as much

as a factor of two). This diﬀerence is largest for low Σ (singular) boundaries.

On the other hand,

−

is always approximately an order of magnitude lower

than

for all misorientations. The static triple junction angles are nearly

independent of misorientation in this two-dimensional Lennard-Jones system

and are very close to the isotropic limit of θ =60

◦

. The dynamic triple junc-

tion angle θ

varies from a low of 44

◦

± 1

◦

to a high of 59

◦

± 1

◦

,andfrom

5.9 Simulation of Triple Junction Motion 505

(a)

(b)

(a)

(b)

FIGURE 5.39

Atomic conﬁgurations during the migration of a ϕ =38.2

◦

(Σ = 7) “+” ge-

ometry triple junction (T =0.125ε/k

,w=25r

)attwoinstantsoftime:

(a) t = 450τ and (b) t = 2150τ. The dynamic triple junction angles were

measured to be θ

=47

◦

in (a) and θ

=48

◦

in (b) [440].

(a) (b)(a) (b)

FIGURE 5.40

Atomic conﬁgurations during the migration of a ϕ =38.2

◦

(Σ = 7) for the “–”

geometry triple junction. The dynamic triple junction angles were measured

to be θ

−

=72

◦

in (a) and θ

−

=71

◦

in (b) [440].