Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

486 5 Computer Simulation of Grain Boundary Motion

time step. Only displacements beyond the nearest-neighbor(NN)-distance are

considered diﬀusive and used to calculate the GB diﬀusive MSD at time t.If

considered diﬀusive the displacement of that atom is counted to the GB MSD,

and the position at time t is kept as the new reference position for the follow-

ing time step. Accordingly, only the diﬀusive MSD of GB atoms is determined.

Apart from GB sliding, GB migration events occur during such simulations as

well although no explicit DF has been introduced. Nevertheless, the analysis

scheme presented is capable of separating atomic displacements due to GB

migration and GB sliding from the diﬀusive GB displacement data.

Once the GB diﬀusive MSD data are determined, the GB self-diﬀusion co-

eﬃcient, D

, is calculated from Eqs. 5.30 and 5.31

MSD(t, t

SSD(t, t

)



j=1

(t + t

) − r

))

(5.30)

= lim

t→∞

MSD

2 · dim · t

(5.31)

where SSD represents the summed-square displacement of all true GB atoms.

The quantity dim deﬁnes the spatial dimension of the diﬀusive process which

is considered three dimensional because at high temperatures the diﬀusive

jumps become three dimensional.

Eq. (5.30) implies that the diﬀusive GB MSD is normalized to the number

of GB atoms, N

. Unfortunately, the deﬁnition of the GB region and its

width as well as the number of GB atoms is not a simple and unambiguous

task. In the following it will be shown that it is not necessary to normalize

the GB MSD data directly to the number of GB atoms but rather to the GB

area. Hence, Eq. (5.30) serves as the starting point to derive the ﬁnal equation

to determine the GB self-diﬀusion coeﬃcient.

Quantifying N

is achieved by approximating N

through the GB area

, the GB width δ and the atomic volume Ω

fcc

. The number of GB atoms

is given by

≈

· δ

fcc

(5.32)

Furthermore, the temporal evolution of the GB diﬀusive MSD and SSD data

is expected to be linear in time, and so in Eq. (5.31) the average over ...

becomes irrelevant for the calculation. Then, the equation for the GB self-

diﬀusion coeﬃcient, D

,isgivenby

δ · D

fcc

= lim

t→∞



DGB

j=1

(t) − r

=0))

· 2 ·dim · t

= lim

t→∞

SSD

· 2 ·dim ·t

(5.33)

Here N

DGB

represents only the diﬀusive GB atoms according to the selection

scheme mentioned. Evidently, D

can not be obtained separately rather only

5.7 Grain Boundary Diﬀusion 487

data on

δ· D

fcc

can be determined. The expression

δ· D

fcc

is obtained from a

plot of SSD vs. time where the slope multiplied by the factor

2·dim·A

yields

δ· D

fcc

5.7.2 Activation Energies

From the temporal evolution of the diﬀusive SSD for each of the studied [001]

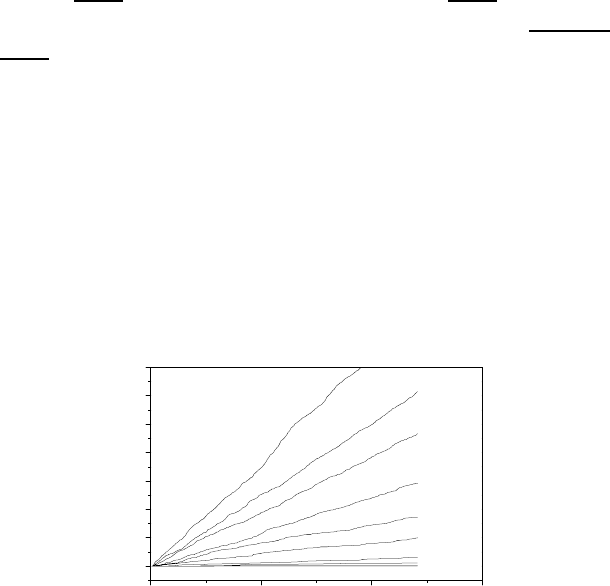
twist GBs, the GB self-diﬀusion coeﬃcients were determined. In Figs. 5.25

and 5.26 the diﬀusive GB SSD data were normalized to twice the GB area,

2 · A

, in order to be representative for the later on to determine GB self-

diﬀusion coeﬃcient D

. It is necessary to use the GB area twice since two

[001] twist GBs are present in the simulation box because of the applied 3D

periodic boundary conditions.

0 400 800 1200

650 K

600 K

750 K

850 K

950 K

700 K

800 K

900 K

1000 K

29 [001] Twist GB

GB self-diffusion

LJ 3D periodic BC

SSD / 2A

[1]

t[ps]

FIGURE 5.25

Total diﬀusive SSD per GB area of the Σ29 [001] 43.60

◦

twistGBatdiﬀerent

temperatures.

At intermediate and high temperatures the diﬀusive jumps of atoms oc-

curred no longer exclusively in-plane but very often out-of-plane. Also, the

GB self-diﬀusion coeﬃcient can only be determined as a product with the GB

width δ which is temperature dependent [533].

Fig. 5.27 presents the GB self-diﬀusion data of the Σ29 twist GB. The data

are representative for high-angle twist GBs since they exhibit one important

aspect. For the Σ29 and Σ5 twist GBs there is a low temperature and a high

temperature regime for both GB self-diﬀusion and GB migration. This is best

seen for the GB self-diﬀusion data of the Σ29 twist GB in Fig. 5.27.

The determined temperature dependence of the GB diﬀusion coeﬃcient

is presented in an Arrhenius plot in Fig. 5.28. From a linear ﬁt of the data

the activation parameters for GB diﬀusion of these [001] twist GBs, namely

488 5 Computer Simulation of Grain Boundary Motion

0 400 800 1200 1600 2000

0,0

0,1

0,2

0,3

700 K

800 K

900 K

1000 K

181 [001] Twist GB

GB self-diffusion

LJ 3D periodic BC

SSD / 2A

[1]

t[ps]

FIGURE 5.26

Total diﬀusive SSD per GB area of the Σ181 [001] 6.03

◦

twistGBatdiﬀerent

temperatures.

11 12 13 14 15 16 17 18 19 20

-5

-4

-3

-2

high T regime

low T regime

600 K

650 K

750 K

850 K

950 K

700 K

800 K900 K

1000 K

GB self-diusion

29 [001] twist GB

LJ 3D periodic BC

[1/ps]

1/k

T[1/eV]

FIGURE 5.27

Arrhenius plot of the GB self-diﬀusion data of the Σ29 [001] twist GB. Here

the results of the temperature range 600 to 1000 K are given.

5.7 Grain Boundary Diﬀusion 489

10 11 12 13 14 15 16 17 18 19 20

-6

-5

-4

-3

-2

-1

600 K

650 K

750 K

850 K

950 K

700 K

800 K

900 K

1000 K

1100 K

GB Self- Diusion - [001] Twist GBs - LJ 3D periodic BC

Σ 29 Σ 5

Σ 85 Σ 181

[1/ps]

1/k

T [1/eV]

FIGURE 5.28

Arrhenius plot of the GB self-diﬀusion data of the [001] twist GBs. The simu-

lations were done for the LJ potential with 3D periodic BC and in the presence

of no DF.

the GB self-diﬀusion enthalpy and the GB self-diﬀusion pre-exponential fac-

tor, were determined (Table 5.5). A more detailed analysis demonstrates that

for the low-angle twist GBs with lowest misorientation, namely Σ181 and Σ85,

the activation enthalpies again increase with decreasing twist angle (Fig. 5.29).

One may surmise that even for smaller twist angles the activation enthalpy

will rise further or at least stay on a rather high level. In the limit of zero

misorientation the volume self-diﬀusion activation enthalpy of 1.97 eV limit

must be found, of course.

Interesting aspects are the low and high temperature GB self-diﬀusion

regimes of the Σ29 and Σ5 twist GBs. The results with the EAM Doyama

[534] and the LJ potential for the Σ5 illustrate that the activation enthalpies

derived from the LJ and EAM potentials do not diﬀer substantially. A GB

self-diﬀusion data analysis performed on moving GBs driven by explicit DFs

proved that GB self-diﬀusion remained almost identical for stationary and

moving GBs. This is conﬁrmed by recent experimental work [535, 536] and

hence adds further conﬁdence in the data analysis used. The GB self-diﬀusion

data of the Σ5 [001] twist GB in the stationary and moving case is presented

in Table 5.6 for 950 K and 1000 K. The data reveal that GB self-diﬀusion via

vacancies remains the same for non-driven and driven GBs. No eﬀect of the

magnitude of the DF used on the GB self-diﬀusion data was found.

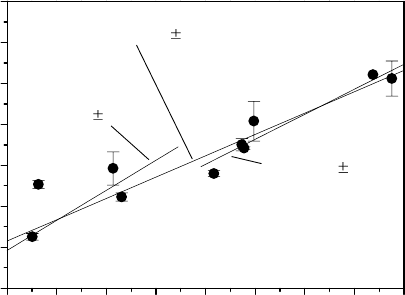
The computed grain boundary diﬀusivities comply with the compensation

eﬀect (Fig. 5.30). In principle all data can be ﬁtted by a single compensation

490 5 Computer Simulation of Grain Boundary Motion

TABLE 5.5

GB Self-Diﬀusion Activation Parameters of the Studied [001] Twist

GBs for the LJ Potential Utilizing 3D Periodic BC

GB plane θ Σ Q

GBD

[eV] ln(

δ· D

[

])

(001) 43.60

◦

29 1.023 ± 0.086 9.518

43.60

◦

29 0.560 ± 0.014 2.342

(001) 36.87

◦

5 1.042 8.757

36.87

◦

5 0.684 ± 0.007 3.560

(001) 28.07

◦

17 0.701 ± 0.030 3.464

(001) 22.62

◦

13 0.816 ± 0.097 3.949

(001) 16.26

◦

25 0.446 ± 0.020 -1.376

(001) 12.68

◦

41 0.252 ± 0.016 -4.979

(001) 8.80

◦

85 0.585 ± 0.081 -1.727

(001) 6.03

◦

181 0.507 ± 0.020 -4.735

Note: The data shown relate to MD ﬁnite temperature simulations

without any DF.

line with a relatively low compensation temperature, though. If only the high

angle boundaries are considered, the compensation temperature compares to

the temperature where structural transitions of the Σ5 and Σ29 boundaries

were found.

5.7.3 Temperature Eﬀects

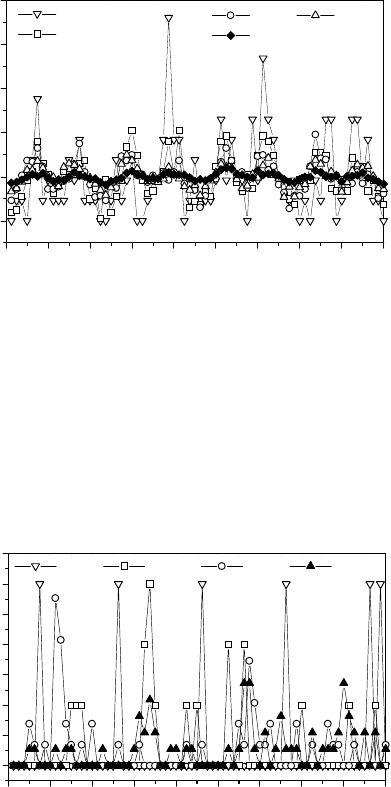
In order to assess how ordered or disordered the GBs remain at elevated tem-

peratures the angular distribution of the GB diﬀusion displacement vectors

can be analyzed. The data presented in Figs. 5.31–5.34 represent the normal-

ized angular distribution of diﬀusional GB jumps of at least the next neighbor

distance. To perform such an analysis, ﬁrst the CNA method is applied to iden-

tify the GB atoms. Then the displacement vectors have to be analyzed. Since

GB sliding might interfere with the analysis scheme, an updating scheme of

the reference position of each GB atom has to ensure that only diﬀusive GB

jumps are oriented for their angular distribution. Once a jump is identiﬁed,

it can be examined with respect to its angular coordinate within the (002)

plane. For this the jump vectors are projected onto the (002) plane, and the

jump angle is determined. The reference coordinate system for this analysis

is the x − y simulation box coordinate system. For a complete MD run, all

jump events and the sum of their angular distributions γ(i) are represented in

a histogram containing 72 classes of 5

◦

. In order to normalize the angular his-

togram, the data of each class are normalized to Γ(i)=

72·γ(i)

i=1

γ(i)

. According

to this normalization, an isotropic uniform angular distribution would assume

the value 1 for each of the 72 angular classes. Usually, at low temperatures

the GBs will have some structural order which has to be reﬂected in the dif-

5.7 Grain Boundary Diﬀusion 491

0 5 10 15 20 25 30 35 40 45

0,0

0,2

0,4

0,6

0,8

1,0

1,2

Σ 181

Nomura and Adams for Cu EAM

and This work for LJ 3D per. BC

GB Self Diusion of Cu [001] Twist GBs

Σ 65

Σ 85

Σ 41

Σ 25

Σ 13

Σ 17

Σ 5

GBD

[eV]

[°]

FIGURE 5.29

Misorientation dependence of the activation enthalpy of GB self-diﬀusion of

the [001] twist GBs studied. The data shown represent the results of the LJ

3D periodic BC simulations of this work and the results by Nomura [532] as

a reference.

TABLE 5.6

GB Self-Diﬀusion Coeﬃcient Determined from GB Migration

Simulations of the Σ5 [001] Twist GB at 950 K and 1000 K

T p

corr

δ D

/Ω

[K] [0,001 eV/atom] [1/ps]

950 0,00 0,0086368

950 3,20 0,0093457

950 6,38 0,0086679

1000 0,00 0,0143417

1000 3,15 0,0137255

1000 6,21 0,0137216

Note: Here the results of the LJ simulations in the presence

of an OCDF, p

corr

, are presented. For simulation runs at ﬁxed

temperature but diﬀerent DFs, the GB diﬀusion coeﬃcient

remains the same. No systematic eﬀect of the magnitude of

the DF is observed on the GB diﬀusion coeﬃcient.

492 5 Computer Simulation of Grain Boundary Motion

-6 -4 -2 0 2 4 6 8 10

0,0

0,2

0,4

0,6

0,8

1,0

1,2

1,4

Σ 181

= 850 483 K

= 708 105 K

Σ 29

Σ 85

[001] Twist GBs

GB Self-Diusion

LJ 3D per. BC

= 603 65 K

GB Diusion

[eV]

ln (

(0) /

[1/ps] )

FIGURE 5.30

Compensation plot of the GB self-diﬀusion data for the [001] twist GBs stud-

ied. Three linear data ﬁts were done. One data ﬁt of the overall data yielded

605 K for the compensation temperature, a data ﬁt of only the high-angle GB

data yielded 708 K, and ﬁnally a ﬁt of only the low-angle GB data yielded

850 K.

5.7 Grain Boundary Diﬀusion 493

fusional data.

0 40 80 120 160 200 240 280 320 360

[001] 29 Twist GB : LJ 3d per. BC

600K 650K 700K 750K

800K 900K 950K 1000K

(

) [1]

[°]

FIGURE 5.31

Angular distribution of the diﬀusion jump vectors of the Σ29 [001] 43.60

◦

twist GB at diﬀerent temperatures.

The analysis relies on the fact that discrete single GB diﬀusional jumps can

be identiﬁed within the system. Typically, only after every 1000 time steps

the positions of all atoms in the system are stored. For high temperatures this

means that not every single jump event can be identiﬁed, since numerous jump

events may have occurred within the time range of 1000 time steps. Never-

theless, the approach is capable of identifying diﬀusional GB jump events and

yields solid data on their angular distribution. From the angular distribution

two main conclusions can be drawn:

(1) All high-angle GBs, especially the Σ29 and Σ5, seem to undergo a struc-

tural transition far below the melting temperature.

(2) Low-angle GBs seem to remain crystalline throughout the temperature

range studied. The thermal weakening of the GB structure was less pro-

nounced than in the case of high-angle [001] twist GBs.

494 5 Computer Simulation of Grain Boundary Motion

0 40 80 120 160 200 240 280 320 360

700 K

800 K

5 [001] Twist GB : LJ 3D per. BC

900 K 1000 K

1100 K

(

) [1]

[°]

FIGURE 5.32

Angular distribution of the diﬀusion jump vectors of the Σ5 [001] 38.87

◦

twist

GB at diﬀerent temperatures.

0 40 80 120 160 200 240 280 320 360

85 [001] Twist GB : LJ 3D per. BC

700 K 800 K 900 K 1000 K

(

) [1]

[°]

FIGURE 5.33

Angular distribution of the diﬀusion jump vectors of the Σ85 [001] 8.80

◦

twist

GB at diﬀerent temperatures.

5.8 Atomic Mechanisms 495

0 40 80 120 160 200 240 280 320 360

181 [001] Twist GB : LJ 3D per. BC

700 K 800 K 900 K 1000 K

Γ(Φ) [1]

Φ [°]

FIGURE 5.34

Angular distribution of the diﬀusion jump vectors of the Σ181 [001] 6.03

◦

twist GB at diﬀerent temperatures.

5.8 Atomic Mechanisms

5.8.1 GB Migration of [001] Twist Boundaries

The simulations revealed several GB migration mechanisms:

(1) Collective shuﬄe mechanism of four atoms for the Σ29, Σ5 and Σ17 GBs.

(2) Dislocation-based mechanism for the Σ41, Σ85 and Σ181 GBs.

(3) Neither of the two mechanisms are hard to identify for Σ13 and Σ25 GBs.

The Σ29, Σ5 and Σ17 twist GBs moved by a collective shuﬄe mechanism at

least at low and intermediate temperatures. The elementary act of the col-

lective shuﬄe mechanism is a cooperative four atom movement. Majid and

Bristowe [537] were the ﬁrst to report a shuﬄe mechanism for the Σ5 [001]

twist GB.

The migration of the Σ41, Σ85 and Σ181 twist GBs was found to be con-

nected to the motion of their screw dislocation networks which can be char-

acterized as follows :

(a) The GB structure in the temperature range studied (700 K to 1000 K)

consisted of a discrete network of screw dislocations. This network was even

present at the highest applied temperatures.

(b) Normally no jumps of atoms across the GB were observed during GB

migration even at the highest temperatures studied. This shows that the GB

migration mechanism was predominantly conﬁned to each (002) plane. This

behavior is quite diﬀerent from high-angle twist GBs at elevated tempera-

tures.

◦

)twistGB