Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 405

0 100 200 300 400 500 600 700 800

time [s]

[

]

250 C

300 C

0 50 100 150 200 250 300 350 400

time [s]

[

]

300 C

320 C

0 100 200 300 400 500 600 700 800

time [s]

100

120

140

160

[

]

250 C

0 50 100 150 200 250 300 350 400

time [s]

100

120

140

160

[

]

300 C

0 100 200 300 400 500 600

time [s]

100

120

140

160

[

]

300 C

0 20 40 60 80 100 120 140

time [s]

100

120

140

160

[

]

320 C

(a)

(b)

0 100 200 300 400 500 600 700 800

time [s]

[

]

250 C

300 C

0 50 100 150 200 250 300 350 400

time [s]

[

]

300 C

320 C

0 100 200 300 400 500 600 700 800

time [s]

100

120

140

160

[

]

250 C

0 50 100 150 200 250 300 350 400

time [s]

100

120

140

160

[

]

300 C

0 100 200 300 400 500 600

time [s]

100

120

140

160

[

]

300 C

0 20 40 60 80 100 120 140

time [s]

100

120

140

160

[

]

320 C

(a)

(b)

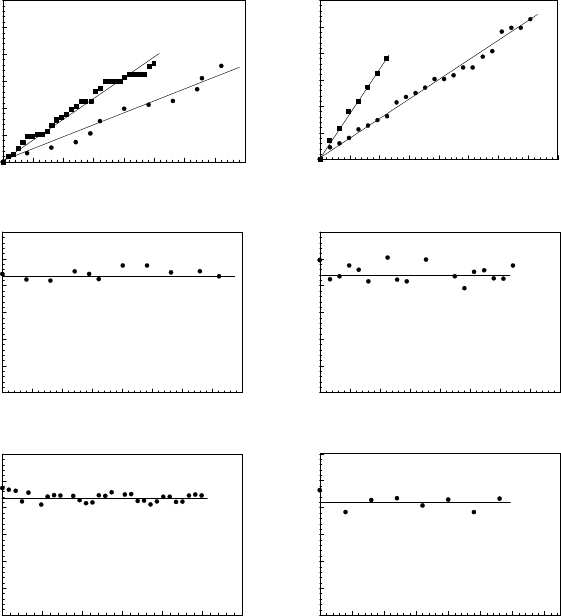
FIGURE 4.53

(a) Displacement and (b) vertex angle 2Θ vs. time for triple junction (a)

TP-G1 and (b) TP-G3 with a conﬁguration of Fig. 4.51b at two diﬀerent

temperatures.

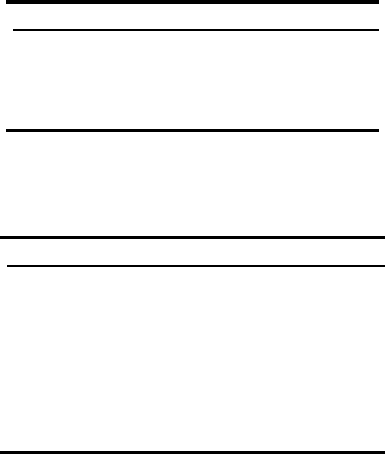
406 4 Thermodynamics and Kinetics of Connected Grain Boundaries

TABLE 4.8

Misorientation of Three Contiguous

Grains at Investigated Junctions

Junction GB I GB II GB III

TP-S2 19

◦

[02

1] 43

◦

[

3] 39

◦

[

TP-S3 35

◦

[310] 53

◦

[

4] 46

◦

[

TP-G1 28

◦

[

3] 31

◦

[

100] 30

◦

[

TP-G3 26

◦

[014] 23

◦

[

100] 12

◦

TABLE 4.9

Parameters of Motion of the Investigated

Boundary System with Triple Junction

Junction T(

◦

C) v(μm/s) 2Θ Λ

TP-S2 250 0.08 49 1

300 0.17 (0.35) 79 2

TP-S3 250 0.10 82 3

300 0.15 116 37

TP-G1 250 0.05 127 0.9

300 0.08 127 0.9

TP-G3 300 0.15 129 0.7

320 0.35 124 2

Λ conﬁrms the results of computer simulations (Fig. 4.54), where the Λ de-

pendency of n

∗

— the topological class for which

S = 0 — was constructed.

However, the direct and conclusive way to estimate quantitatively the drag

eﬀect of triple junctions on grain growth is to measure the rate of area change

of individual grains.

To attribute the rate of grain area change to triple junction drag and specif-

ically to a deﬁnite value of Λ, some rather strict criteria should be fulﬁlled in

experiment. In particular, the grain growth should be driven in a boundary

regime (Eqs. (4.82, 4.85)), and the motion of the triple junction has to be in

steady state.

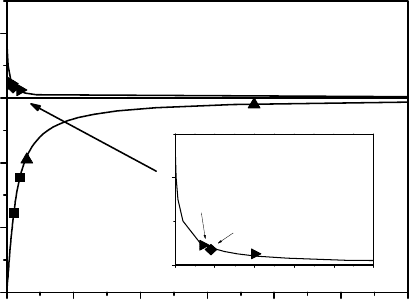
It was shown that at constant temperature S ∼ t. This conﬁrms the bound-

ary kinetics of the observed grain growth [429]. The main result, obtained in

[429], is the experimentally measured diagram

S = f(n) (Figs. 4.54 and 4.55).

The diagram revealed that the rate

S was not constant for a given n,asit

needs to be in accordance with the Von Neumann-Mullins concept, but follows

the relations (4.82, 4.85), which take into account the triple junctions drag.

Apparently, the grains which exhibited higher rates

S were not (or were less)

aﬀected by triple junctions. The Von Neumann-Mullins limit is represented in

the diagram of Fig. 4.55 by the straight line connecting the maximal values

S and the point

S =0forn = 6. The slope of this line is determined

by the reduced grain boundary mobility A

= m

γ. The measured value of

4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 407

0 102030405060

012345

TP-G3, 300 °C

TP-G3, 320 °C

TP-G1, 250 °C, 300 °C

TP-S3, 300 °C

TP-S3, 250 °C

TP-S2, 250 °C

TP-S2, 300 °C

FIGURE 4.54

Vertex angle Θ vs. criterion Λ. The symbols denote the measured values for

the analyzed junctions; the lines are calculated according to Eqs. (4.81 and

4.82).



∼ 10

−10



is in a good agreement with mobility data of random grain

boundaries in Al [450].

On the other hand, if A

is known, the values of Λ can be calculated for

each experimental point from equations (4.82) and (4.85). The more a meas-

ured value of

S deviates from the Von Neumann-Mullins limit the stronger

the drag eﬀect exerted by triple junctions and, respectively, the smaller the

value of Λ.

The experimental results are in a good agreement with predictions of vertex

simulations of grain growth, in particular with Fig. 4.41 [442]. We would like

to stress again that due to the ﬁnite mobility of the triple junctions there

is no more a unique linear dependence between grain growth rate and the

topological class of the grain; in other words, the growth rate

S does not only

depend on the topological class of the grain but on the criterion Λ as well.

4.6.6.7 How to Evaluate the Mobility of Grain Boundary

Junctions? Phenomenological Approach

The main consequence of the consideration given above can be formulated as

follows: in order to predict and describe the kinetics and geometry of grain

microstructure evolution the mobility of grain boundary junctions needs to

be known.

Undoubtedly, the most correct way to determine the mobility of boundary

408 4 Thermodynamics and Kinetics of Connected Grain Boundaries

-2x10

-10

-1x10

-10

1x10

-10

dS/dt [m

/s]

234567891011

300 °C

10,5

0,2

0,3

0,25

224

118

1,2

3,5

FIGURE 4.55

Rate of grain area change dS/dt vs. topological class n of a grain for 300

◦

The values of Λ are given next to the data point.

junctions is the study of a grain boundary system with a single junction in a

steady-state motion or a certain grain of deﬁned topological class in the course

of grain growth [183, 436]. However, in general this is a cumbersome procedure

which requires a sophisticated technique of grain microstructure analysis and

the results of independent measurements of grain boundary mobility.

In [447] a rather simple approach was used for evaluation of the mobility

of grain boundary junctions, namely from the temporal evolution of the grain

size. Let us consider the motion of a grain boundary driven by grain boundary

curvature κ with triple and quadruple junctions which have their own mobility.

The motion of such a boundary can be considered as the motion of a boundary

with mobile defects [441, 447]. The velocity of such a boundary is given by

V = P

eﬀ

(4.92)

where P

eﬀ

is the eﬀective driving force for grain growth

eﬀ

= γκ −

−

(4.93)

and a

are the spacings of the respective junctions. Since a

and a

are of the same order of magnitude we assume for simplicity a

= a

= a in

the following. f

and f

are the drag forces of triple and quadruple junctions,

respectively. In accordance with the Nernst-Einstein relation

(4.94)

4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 409

we arrive at





= m

γκ (4.95)

Eqs. (4.92)–(4.95) yield

V =

γκ

(4.96a)

where Λ



> − <R



(<R>− <R

>)+

<R>

= t

(4.96b)

where <R>is the mean geain size.

Eqs. (4.99a) or (4.99b) deﬁne the diﬀerent types of grain growth kinet-

ics in polycrystals. The ﬁrst one is the well-known grain boundary kinetics:

 1, the velocity V is proportional to the grain boundary curvature,

and the mean grain size increases in proportion to the square root of the an-

nealing time: V =

d<R>

∼

<R>

→<R>∼

√

t. If grain boundary motion

is controlled by the mobility of triple junctions (

 1and



), the

velocity V is constant: V =

d<R>

=const. →<R>∼ t. Finally, if the mo-

bility of the quadruple junctions (points) determines the motion of the grain

boundary system (

 1and



)thevelocityV is proportional

to the radius of curvature: V =

d<R>

∼<R>→<R>∼ e

. Under grain

boundary kinetics we observe the classical grain growth kinetics, which is to

hold for rather large grains. The schematic diagram of the mean grain size vs.

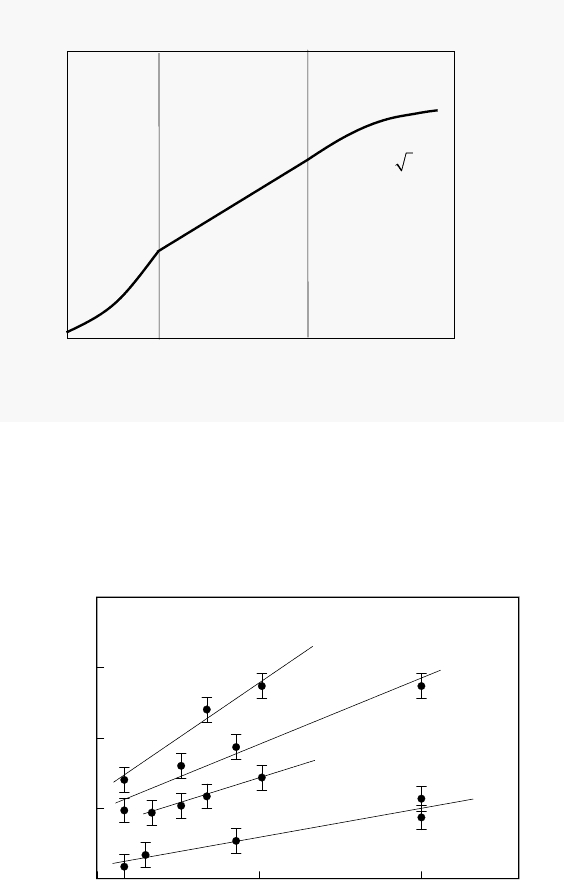
time dependence of diﬀerent kinetic regimes is given in Fig. 4.56.

There is only a very restricted number of studies where the grain growth in

nanocrystalline and ultraﬁne-grained materials was observed, and much less

where it was quantitatively evaluated. Experimental data relevant to such ki-

netics were actually obtained for grain growth in thin (∼ 1000

A) silver ﬁlms

[415]. Fig. 4.57 shows the dependence of the mean grain size on annealing time

at the early stage of grain growth. For all temperatures investigated the mean

grain size changed linearly with annealing time. At a later stage of annealing,

when the mean grain size reached a suﬃciently large value, corresponding to

Fig. 4.55, the kinetics were ruled by the grain boundary mobility, and the

linear time dependence was replaced by a parabolic relationship.

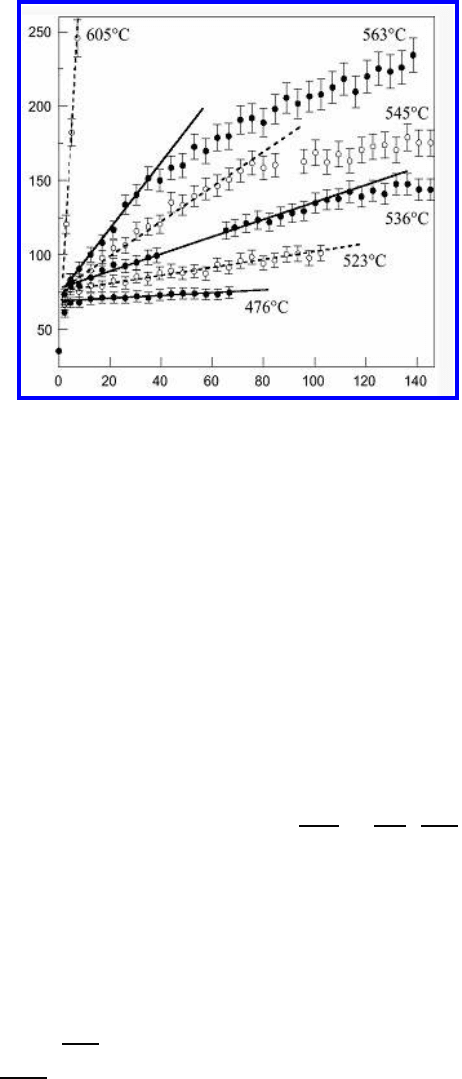
In Fig. 4.58 the results of grain growth in nanocrystalline iron are pre-

sented [451, 452]. In [451, 452] grain growth for a rather small grain size is

characterized by a linear dependence of the mean grain size on annealing

time. It should be stressed that at large annealing time the linear dependence

<R>∼ t transforms to the classical grain boundary kinetics <R>∼

√

410 4 Thermodynamics and Kinetics of Connected Grain Boundaries

Quadruple

Junction

Regime

Triple Junction

Regime

Grain Boundary

Regime

Time, t

<R> ~ e

<R> ~ t

Quadruple

Junction

Regime

Triple Junction

Regime

Grain Boundary

Regime

Time, t

<R> ~ e

<R> ~ t

FIGURE 4.56

Grain growth kinetics at diﬀerent regimes.

0 0.5 1

time [h]

[

]

350°C

400°C

500°C

600°C

FIGURE 4.57

Temporal evolution of the mean grain size <R>in thin silver ﬁlms [415].

4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 411

Annealing time (min.)

R (nm)

Annealing time (min.)

R (nm)

FIGURE 4.58

Mean grain size (radius) in nanocrystalline iron vs. annealing time [452].

There are indications that in the course of grain growth in nanocrys-

talline materials quadruple junction kinetics were also observed [453, 454].

The quadruple junction mobility m

γ extracted from the experimental re-

sults of [453] is given in [447]: m

∼

2 · 10

−4

−1

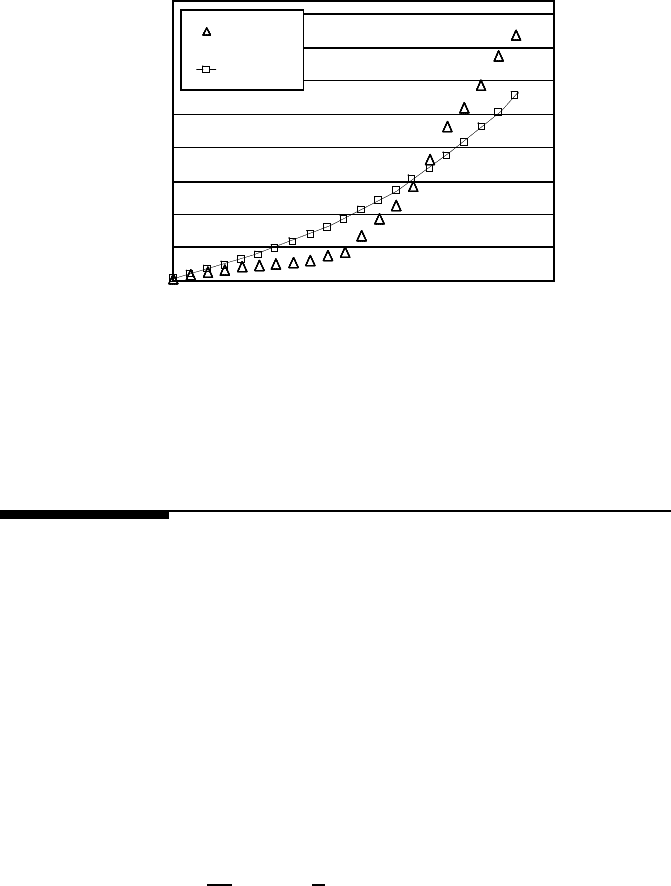
In Fig. 4.59 the experimental data of grain growth in nanocrystalline Pd are

presented [454]. We would like to draw the reader’s attention to the distinctive

property of the experimental curve: at the early stage of annealing the shape of

the curve is concave. The approach discussed gives us the possibility to extract

the values of the triple junction and quadruple junction mobility from the time

dependency of the mean grain size: m

γ =3·10

−11

−1

; m

γ =3·10

−5

−1

The agreement between equation (4.96a) for



and exper-

iment (Fig. 4.59) is reasonable [454]. This agreement can be improved if the

initial region of the curve, where grain growth does not take place in reality,

is neglected.

The inverse problem has been investigated by Novikov. He studied by com-

puter simulation the grain growth in 2D and 3D systems for diﬀerent grain

sizes as well as triple junction and quadruple point mobilities [445, 446]. For

a rather small grain size and (or) low triple junction and quadruple junction

mobility the curves <R>−t have just the same peculiarities: linearity for

rather small Λ

and an exponential dependence <R>∼ exp(t)for

small Λ

412 4 Thermodynamics and Kinetics of Connected Grain Boundaries

Experimental

Exponential

0 7200

14400

21600

720006480050400

57600432003600028800

8.00

48.00

43.00

38.00

33.00

28.00

23.00

18.00

13.00

Time (s)

Grainsize(nm)

Experimental

Exponential

0 7200

14400

21600

720006480050400

57600432003600028800

8.00

48.00

43.00

38.00

33.00

28.00

23.00

18.00

13.00

Time (s)

Grainsize(nm)

Experimental

Exponential

0 7200

14400

21600

720006480050400

57600432003600028800

8.00

48.00

43.00

38.00

33.00

28.00

23.00

18.00

13.00

Experimental

Exponential

Experimental

Exponential

Experimental

Exponential

0 7200

14400

21600

720006480050400

57600432003600028800

8.00

48.00

43.00

38.00

33.00

28.00

23.00

18.00

13.00

Time (s)

Grainsize(nm)

FIGURE 4.59

“Grain growth” in nanocrystalline Pd [454];  — experiment,  —

Eq. (4.99b).

4.7 Grain Growth in 3D Systems

4.7.1 Analytical Approaches

As mentioned in Sec. 4.6.5 a direct transfer of the Von Neumann-Mullins

relation to 3D systems is impossible. However, the beauty and mathematical

clarity of the Von Neumann-Mullins relation encouraged a number of attempts

to search for a 3D analogy of this relation. All approaches share the assump-

tion that a 3D polycrystal can be represented as an assembly of polyhedra.

However, as shown in [545], a polycrystal cannot be completely constructed

from convex polyhedra, rather than piecewise convex or concave. First of all

let us consider grain growth in a case when the grain system is nearly two

dimensional. Levine et al. represented the Von Neumann-Mullins relation as

[544]

= m



(n − 6) + S

¯κ



(4.97)

where ¯κ

is the Gaussian curvature measured over the area of a grain. For

¯κ

> 0 the area of the grains at the surface will increase exponentially, whereas

for the grains inplane the area will change linearly with time. Finally, the en-

tire surface will constitute a single grain. On the other hand the negative

Gauss curvature (¯κ

< 0) stabilizes the grain microstructure (see Eq. (4.97))

for a deﬁnite grain area.

Mullins [546] proceeded from the assumption that grain growth in 3D sat-

4.7 Grain Growth in 3D Systems 413

isﬁes the hypothesis of statistical self-similarity and that the grain boundary

normal velocity at any point of the grain boundary is proportional to the

local mean curvature. The volume rate of change

V for a given grain can be

described as

V =





dS (4.98)

and integration over all grain faces results ﬁnally in the kinetic equation

V · V

−1/3



4π



1/3

γG

(N) · G

(N) (4.99)

where N is the number of faces of the polyhedron considered

(N)=π/3 − 2arc tan



1.86(N −1)

1/2

N − 2



(4.100)

(N)=5.35n

2/3



N − 2

2(N −1)

1/2

−

(N)



The dependency (4.99) manifests some interesting features, in particular,

grains with N ≤ 13 shrink whereas grains with N ≥ 14 grow. The consider-

ation reﬂects the major properties of analogous approaches: the ﬁnal kinetic

relation is based on a large number of approximations, the most essential of

which is the substitution of a real 3D grain by idealized polyhedra, bordered

by ﬂat faces, and so on.

Hilgenfeldt’s approach [545] is based on the famous theorem of Hermann

Minkowski from 1903. Minkowski had shown that the mean curvature over the

surface of a convex body is linked to the caliper radius, which is the distance

between the coordinate origin (the center of mass of the body) and the plane

touching the body in the direction (Θ,φ)



4π

c(Θ,φ)dw =



HdA (4.101)

where the integrals are over all solid angles and the total area of the convex

body.

Hilgenfeldt applied Eq. (4.101) to two diﬀerent polycrystals: to polyhedra

K with curved edges and its skeleton polyhedron K

, i.e. a polyhedron with

the same vertex positions, however, with ﬂat surfaces to obtain





−1/3

= m

γG(N) (4.102a)

where

G(N)=

3[(n − 2)tanπ/η

]

2/3

tan

1/3

(χ

)

1/3

· (π/3 − χ

)

414 4 Thermodynamics and Kinetics of Connected Grain Boundaries

with η

= G −

and

= 2 arc tan



4sin

(π/χ

)

1/2



(4.102b)

Glicksman and Rios [547]–[551] developed the so-called “average N-hedra”

(ANH) model. The authors [547]–[551] describe ANH as a symmetric, i.e.

isometric N -hedron, consisting of N identical faces, meeting at 3(N −2) pairs

of identical symmetrical vertices, each separated from adjacent vertices by

constant distance. In other words, an ANH is a polycrystal of equidistant

(from volume centroid) vertices. Every pair of adjacent faces intersects at

the topologically required average internal dihedral angle of 120

◦

. Each ANH

in this inﬁnite set manifests unique geometric properties, all of which are

determined by the index N ≥ 4 [547]–[551]. In this model all grains in a

polycrystal have the same vertex-to-vertex distance.

The expression for the grain volume rate of change renders





−1/3

= m

γc



√

N −



(4.103)

where c

∼

1.51 and N

∼

13.397 is the critical number of faces or critical

topological class of ANH; this polyhedron would neither grow nor shrink.

It is emphasized that all approaches introduced so far are based on the

assumption that a 3D polycrystal can be represented by a system of convex

bodies (polyhedra).

In 2007 MacPherson and Srolovitz [552] derived a strict relation between

the rate of grain volume change and the topological and geometrical charac-

teristics of a polycrystal. It was shown that the integral curvature H (the sum

of the principal curvatures) for a domain D with mean width L(D) bounded

by a surface ∂D consisting of smooth surfaces that meet along curves (edges)

with dihedral exterior angle α = π/3 measured in the plane perpendicular to

the edges with length e

(D) can be expressed as [552]



∂D

HdA=2π



L(D) −



i=1

(D)



(4.104)

The signiﬁcance of average mean curvature for quantitative metallography

was already shown by Cahn [553]. In particular it was described how the

average value of the mean curvature of surfaces in a specimen can be pre-

cisely determined by simple measurements performed on random sections or

on projections of these surfaces. The inverse problem reads

¯κ

=(1/L)



d (4.105)

where κ

is the curvature, κ



(1+y

2

)

3/2

, d =

1+y

2

dx,andL =

d

is the total length of the curve. The integral in Eq. (4.105) can be called the