Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 385

As in the previous case, Eqs. (4.25) and (4.75) fully deﬁne the problem con-

sidered.

y(x)=−

ln sin Θ

arc cos



·ln sin Θ



(4.77)

The velocity of steady-state motion of the system is

V = −

ln sin Θ (4.78)

The length x

replaces the role of the grain size a in the previous case

(Fig. 4.37) or

= y (x

)=−

ln sin Θ

arc cos



ln sin Θ



= −

ln sin Θ



− Θ



(4.79)

From Eqs. (4.76) and (4.78) we obtain Λ, which describes the inﬂuence of the

triple junction mobility on grain boundary migration

−

ln sin Θ

1 − 2cosΘ

= Λ (4.80)

Obviously, for Λ  1, when the boundary mobility determines the kinetics of

the system, the angle Θ tends to its equilibrium value (π/3).

Again, the angle Θ changes when a low mobility of the triple junction

starts to drag the motion of the boundary system. However, as evident from

Eq. (4.80) and Fig. 4.6, in this case the steady-state value of the angle Θ

increases as compared to the equilibrium state. (Otherwise the triple junction

would move in the negative direction of the x-axis, increasing the free energy

of the system.)

For Λ  1 the angle Θ (Eq. (4.80)) tends to approach π/2. The dependency

Θ = Θ(Λ) for both n<6andn>6 are shown in Fig. 4.6.

Such an increase of the angle Θ also decreases the magnitude of (n −2π/Θ)

in Eq. (4.74), in other words, it decreases the “eﬀective” magnitude of the

topological class of the growing grain with n>6. Consequently, microstruc-

tural evolution will slow down due to triple junction drag for any n-sided

grain. The only exception holds for n = 6, since a hexagonal grain structure

becomes unstable when the contact angle 2Θ =2π/3. Since the actual mag-

nitude of Θ is determined by the triple junction and grain boundary mobility

as well as the grain size and is independent of the number of sides of a grain,

there is no unique dividing line between vanishing and growing grains with

respect to their topological class anymore, like n = 6 in the VN-M approach.

The generality of the approach considered and the diversity of the conse-

quences should be stressed. In particular, the result expressed in Eq. (4.71)

does not depend on the shape of the moving boundaries: the rate of grain area

change along with the sign of the right-hand side of Eq. (4.71) is determined

only by the number of the adjacent (neighboring) grains, or, what is same,

by the topological class of the grain — the number of triple junctions of the

grain.

386 4 Thermodynamics and Kinetics of Connected Grain Boundaries

4.6.6.1 Triple Junction Motion and Grain Microstructure Evolu-

tion

The classical concepts of grain growth in polycrystals are based on a domi-

nant role of grain boundaries. Since metals are not transparent, we are used

to imaging crystalline microstructures by means of 2D sections, for instance

in optical micrographs.

The 2D model of grain growth provides the basis for our understanding of

the thermodynamics and kinetics of grain microstructure evolution. However,

2D grain microstructures are not pure mathematical abstractions. In modern

materials science objects with 2D grain structure are physically meaningful

and have achieved great importance. Metal sheet, thin ﬁlms, coatings and thin

layers are prominent examples of objects with 2D grain microstructure.

For a variety of problems it is possible to obtain an exact physical solution

for 2D microstructures. The most famous example is the VN-M relation which

was considered above. This relation is based on three fundamental assump-

tions.

The ﬁrst assumption agrees with the described uniform boundary model

and is likely to be realized in many cases. Of course, grain boundary mo-

bility is signiﬁcantly aﬀected by grain boundary character (see, for instance

Chapter 3), and an anisotropy of grain boundary properties manifests itself

also in grain microstructure evolution [422]. Nevertheless, in polycrystals with

random texture and in commercial alloys non-special boundaries are likely to

prevail [273, 424]. For a more reﬁned analysis, anisotropic boundary proper-

ties also have to be taken into account; however, they will not change the

fundamental conclusions of the approach presented in the following [425].

The second assumption complies with the principles of absolute reaction

rates. The third assumption — the inﬁnite mobility of grain boundary triple

junctions — is a mere hypothesis and needs to be checked experimentally. For

this it is necessary to measure the triple junction mobility.

As shown in the previous paragraphs the theoretical approaches and exper-

imental technique developed make it possible to measure quantitatively the

mobility of triple junctions [183, 427, 436]. It was shown that the behavior

of a grain boundary system with triple junction is determined by the dimen-

sionless criterion Λ =

. For steady-state motion of the grain boundary

system with triple junction the criterion Λ can be expressed as a function of

the angle Θ at the tip of triple junctions (relation 4.30). The line between Λ

and Θ makes it possible to measure the value of Λ and, in turn, the triple junc-

tion mobility for diﬀerent metals and grain boundary systems. Experimental

investigations on grain boundary systems with triple junctions in Zn and Al

have shown that the triple junction mobility is ﬁnite and may be low. Molec-

ular dynamics simulation studies of triple junction migration, performed for

the same geometrical conﬁguration as used in real experiments [183, 421, 436],

conﬁrmed that the triple junction mobility, contrary to the VN-M assumption,

can be limited [439, 440] (see Chapter 5). On the whole, the simulations sup-

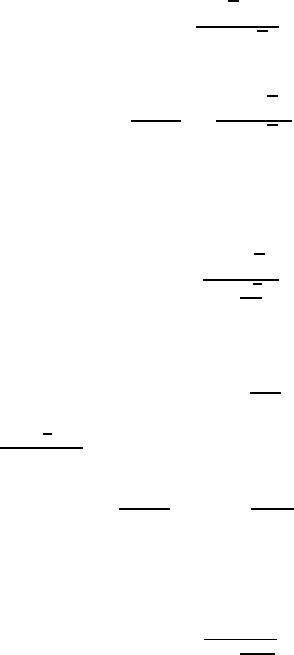
4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 387

port the experimental observations of non-equilibrium triple junction angles

and ascertain a substantial triple junction drag.

4.6.6.2 The Generalized Von Neumann-Mullins Relation

Since the assumptions made to derive the VN-M relation can obviously be vi-

olated it is of interest to consider this relation for the case of non-equilibrium

contact angles at the triple junction. Such an attempt was undertaken in

[427, 441, 442]. To conserve the central idea of the VN-M relation let us con-

sider ﬁrst a situation when the inﬂuence of the triple junction is rather large,

but, nevertheless, the motion of the system can be viewed as grain boundary

motion, since the driving force is still due to grain boundary curvature, i.e.

the triple junction is reduced to a change in the angle Θ (Eq. 4.74)).

Since Λ = Λ(Θ) the relation between the rate of grain area change and the

criterion Λ can be found. In [442] such a relation was derived expanding the

function 2cosΘ − 1 into a power series in the vicinity of Θ = π/3forn<6

and n>6, respectively. For n<6

∼

√

3πΛ

6+3

√

3λ

(4.81)

and, respectively,

S =

γπ



√

3Λ

√

3Λ

− 6



(4.82)

For Λ →∞— free boundary kinetics regime — Eq. (4.82) is identical to the

classical VN-M relation.

The topological class n

∗

of grains for which

S =0isequalto

∗

√

3Λ

√

(4.83)

Evidently n

∗

increases with Λ and for Λ →∞n

∗

→ 6. For n>6

∼

π/3+

ΛB

(4.84)

where B = −

√

ln sin(π/3)

and, correspondingly

∼

γπ





1 −

πΛB



− 6



(4.85)

Apparently, for n<6andforn>6, the equation for the rate of grain area

change becomes identical for Λ →∞;thevalueofn

∗

for n>6reads

∗

1 −

πΛB

(4.86)

388 4 Thermodynamics and Kinetics of Connected Grain Boundaries

FIGURE 4.38

Dependence of n

∗

and n

∗

on Λ.

The drag eﬀect of grain boundary triple junctions results in a change in the

topological limit between the classes of shrinking and growing grains such that

the limit decreases for shrinking grains but increases for growing grains. This

behavior n

∗

(Λ) becomes obvious from Fig. 4.38, where the cases n<6and

n>6 are distinguished as n

∗

(Λ) and n

∗

(Λ), respectively.

4.6.6.3 Grain Stability

Since there is a gap between n

∗

(Λ) and n

∗

(Λ) it is an interesting question

how grains behave with n

∗

(Λ) <n<n

∗

(Λ). From the above discussion it

appears that such grains are not capable of growing or of shrinking (Fig. 4.38),

i.e. grains of the topological classes in the hatched area of Fig. 4.38 will be

stable. This can be understood from the following consideration.

According to Eq. (4.74)

S becomes zero for

Θ=



1 −



(4.87)

For any integer n,Θ(n) is exactly the (half) junction angle for an n-sided

polygon, i.e. Θ = 60

◦





for n =6,Θ=54

◦

for n =5,Θ=45

◦





for

n =4,Θ=67.5

◦



3π



for n =8,etc.

This means for a given (integer) n

∗

the angle Θ corresponds to the (half)

internal angle of an n

∗

-sided polygon, i.e. the boundaries are ﬂat, and without

curvature the polygon is stable. The important point to consider is that the

angle Θ is a dynamical angle, i.e. it develops during motion of the bound-

aries that are connected at the triple junction. Prior to motion boundaries

4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 389

at a triple junction will adjust Θ to attain the equilibrium angle (Θ = 60

◦

Therefore, 6-sided grains have ﬂat boundaries, n<6-sided grains have convex

boundaries, n>6-sided grains have concave boundaries. If the system is al-

lowed to move the curved boundaries will move and adjust Θ to the dynamic

value, which is less than 60

◦

for n<6 and larger than 60

◦

for n>6.

The 6-sided grain will not change since it has ﬂat boundaries to begin

with, so there is no driving force for grain boundary motion and, therefore,

no change of Θ = mπ/3. Let us consider a 5-sided grain under the condi-

tion n

∗

= 4, i.e. a 4-sided grain will attain ﬂat boundaries and, therefore, is

stable (Fig. 4.39). Prior to motion the 5-sided grain has convex boundaries

with π/3 = Θ at the junctions. Triple junction drag will change the angle to

Θ=π/4. Corresponding to n

∗

= 4, the angle Θ = π/4=45

◦

is smaller than

the junction angle for a 5-sided grain with ﬂat boundaries. During the change

of the angle from initially Θ = 60

◦

to Θ = 45

◦

for the given Λ the angle

will pass through Θ = 45

◦

, where the boundaries become ﬂat and the driving

force ceases. The conﬁguration is locked. The junction angle may return to

Θ=60

◦

to establish static equilibrium at the junction, but this will make the

boundary convex and drive the junction angle back to 54

◦

. In essence, if the

5-sided grain were to attain the angle Θ = 45

◦

from initially 60

◦

,itwould

have to change the curvature from convex to concave. For this to happen it

must pass through a ﬂat conﬁguration, where the driving force ceases and the

system becomes locked.

The same holds for a grain with n

∗

> 6. Let us consider n

∗

= 8 and a 7-

sided grain. Initially, Θ is in static equilibrium with Θ = 60

◦

. The boundaries

are concave. Because of n

∗

= 8 the dihedral angle of the 7-sided grain will

change to a terminal 67.5

◦

.AtΘ=

5π

=64.3

◦

the 7-sided grain will arrive

at a conﬁguration with ﬂat boundaries. Again, the boundaries at static equi-

librium are concave. A 7-sided grain for Θ = 67.5

◦

with a Λ corresponding to

∗

= 8 would have convex boundaries. It never can get there, since the change

in curvature requires a transient ﬂat boundary, where the system will become

locked, when only curvature drives the boundary system.

In summary, grains with n-sides and n

∗

<n<n

∗

become locked and

can neither grow nor shrink. This phenomenon might be essential for under-

standing the high stability of grain microstructures in ultraﬁne-grained and

nanocrystalline materials, speciﬁcally in 2D thin layers and ﬁlms. For Λ →∞,

i.e. for Θ = π/3 = const., the border between growing and shrinking grains

is the singular value n

∗

= 6. It dissociates to an interval (between n

∗

and

∗

) for rather small Λ. Such an eﬀect is expected to further stabilize the

grain microstructure. Since Λ depends on grain size, this stabilization is more

pronounced in ﬁne-grained and nanocrystalline systems.

390 4 Thermodynamics and Kinetics of Connected Grain Boundaries

5 Sided grain

−

90°

concave

flat

convex

120°

108°

FIGURE 4.39

Geometry of a 5-sided grain during transition from static to dynamic equilib-

rium for n

∗

=4.

4.6.6.4 Triple Junction Controlled Growth

For a large grain size, or more correctly, for a rather large criterion Λ, the

system moves under boundary kinetics while triple junctions only slightly

disturb grain boundary motion. However, as the criterion Λ decreases, grain

boundary migration and grain growth, respectively, become controlled by the

motion of triple junctions. The triple junction kinetics are characterized by

some distinctive properties which we will discuss in more detail. To begin

with, we will show that under triple junction control in the course of grain

growth in 2D systems the grains will eventually be bordered by straight (ﬂat)

boundaries, i.e. they will assume a polygonal shape.

Let us consider the curvature κ of a grain boundary system with triple

junctions (for conﬁgurations which relate to n<6andn>6). As derived in

[441] for a system with n<6 we obtain for the curvature κ

κ =

−x/ξ+ln sinΘ

2Θ

−(2Θ/a)x

sinΘ =

sinΘ(2cosΘ − 1)e

−(2Θ/a)x

(4.88a)

where ξ

2Θ

.Forasystemwithn>6itwasshownthat

κ =

ln sinΘ

(x/x

)ln sinΘ

(1 − 2cosΘ)e

(x/x

)ln sinΘ

(4.88b)

Since for triple junction kinetics Λ → 0, the grain boundary curvature ¯κ also

approaches zero, i.e. the grain structure of 2D polycrystals comprises straight

grain boundaries. In other words, under triple junction kinetics the grains in

a 2D polycrystal represent a system of contiguous polygons.

More speciﬁcally, as shown in [441], in the framework of triple junction ki-

netics a polygon of arbitrary shape will be transformed into an equilateral

polygon, and any deviation from an equilateral polygon will generate a force

to restore the equilibrium shape. The only exception is a triangle, i.e. a grain

of topological class n = 3 is always unstable and must disappear. Eventually,

4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 391

all other shrinking polygons must by necessity go through this stage, when

grain growth is controlled by the motion of triple junctions.

This phenomenon has important consequences for the development of grain

growth. To demonstrate this we take a look at the evolution of a shrinking

grain in the course of grain growth. The topological class of such a grain must

be lower than 6, taking into account naturally all corrections to the VN-M re-

lation, given above. We emphasize that the transition between boundary and

triple junction kinetics does not only depend on grain boundary and triple

junction mobility, but on the size of a grain as well. When the size of a grain

diminishes progressively there comes a time when boundary kinetics become

replaced by junction kinetics. This will happen to grains of the topological

class n =4orn = 5 which are bound to shrink even after such a transition to

triple junction kinetics. Grains of topological class n = 3 will collapse without

transforming into a regular polygon. Since the kinetics of triple junctions are

signiﬁcantly slower than boundary kinetics, the four- and ﬁve-side polygons

will shrink, and eventually contract to a point although at a markedly smaller

rate. How this phenomenon reveals itself during grain growth will be consid-

ered below.

The ﬁnal stage of grain growth under triple junction kinetics is a regular

n-sided polygon. Let us ﬁnally consider the behavior of a regular n-sided poly-

gon. As shown in [441, 442], the rate of grain area change

S can be expressed

S = −m

γn

Rsin



2π





2sin





− 1



= −2m

γn˜rsin





2sin





− 1



(4.89)

where ˜r and

R are an interior and exterior radius, respectively.

In essence, a limited triple junction mobility always slows down the evolu-

tion of grain microstructure of polycrystals, irrespective of whether the topo-

logical class of the considered grain is smaller or larger than 6. Formally, for

grains with n<6, the sluggish motion of the triple junctions “reduces” the

eﬀective topological class of growing grains, whereas for grains with n>6

the triple junction behavior makes the topological class of vanishing grains

appear larger.

The mere fact that there is a growing grain with triple junctions of low mo-

bility requires the existence of other grains with n<6 to surround it. There

is no point in discussing to which grain their common junction belongs. The

only exception holds for n = 6, since under triple junction control a hexagonal

grain structure with contact angle 2Θ = 2π/3 becomes unstable. Since the ac-

tual magnitude of Λ is determined by the triple junction and grain boundary

mobility as well as by the grain size and is independent of the number of sides

of a grain, there is no unique dividing line between vanishing and growing

grains with respect to their topological class anymore, like n = 6 in the VN-

M approach. As has been detailed above for suﬃciently small Λ the border

between shrinking and growing grains degenerates to an interval bounded by

392 4 Thermodynamics and Kinetics of Connected Grain Boundaries

the lines n

∗

(Λ) and n

∗

(Λ) (Fig. 4.39) which contracts to a point for Λ →∞.

In the following we consider the consequences of the two approaches for the

evolution of grain microstructures. The distinguishing feature of the VN-M

model is the inﬁnite mobility of grain boundary triple junctions. This requires

that grains in a “Von Neumann-Mullins” polycrystals are bordered by curved

boundaries. This should manifest itself in linear dependences of the mean

grain area on time and of the rate of grain area change on the topological

class. For a given reduced boundary mobility A

= m

· γ a grain with topo-

logical number n is characterized by a unique value of its rate of area change

≡

S. The slope of the relation

S(n) is only determined by the reduced

grain boundary mobility:

γπ

In the opposite case, for pure triple junction kinetics the grains in a 2D

polycrystal are bordered by straight lines, i.e. the grain microstructure is rep-

resented by a system of space-ﬁlling polygons. The temporal evolution of such

a system is deﬁned by Eq. (4.89).

A practically relevant and theoretically interesting case is an intermediate

situation, when the triple junction inﬂuence is tangibly large, but neverthe-

less, the evolution of the system can be still considered as governed by grain

boundary motion. In this case the time dependence of the average grain area

<S>is practically linear; however, the rate of grain area change

S is deﬁned

not only by the topological class n but by the criterion Λ as well (Eqs. (4.82)

and (4.83)), respectively. So, there is no unique relation anymore between

and topological class n of the grain; the dependence

S(n) is blurred by the

impact of criterion Λ.

The discussed consequence aﬀorded by the developed approach is probably

the most signiﬁcant one, but the new approach also allows us to make some

more quantitative predictions.

i) Grains are not capable of growing nor of shrinking in the intermediate

situation that manifests itself in the dependency

S =0andn

∗

= n

∗

(Λ).

ii) Under triple junction kinetics grains should be bordered by ﬂat bound-

aries, i.e. straight lines in 2D.

iii) Under triple junction kinetics a system of polygons tends to transform

to a system of equilateral polygons. The only exception is the triangle

which will collapse without transforming into a regular polygon.

iv) For triple junction kinetics the rate of grain area change can be described

by Eq. (4.89).

We would like to remind the reader that both the VN-M model and the model discussed

in [441, 442] are based on the uniform grain boundary and triple junction approach.

4.6 Triple Junction Drag and Grain Growth in 2D Polycrystals 393

4.6.6.5 Computer Simulations

In both theoretical approaches only a single grain and its behavior are consid-

ered in an unspeciﬁed, i.e. average environment. The eﬀect of discrete grain

arrangements was studied by computer simulations of 2D grain growth [442].

Curvature and boundary-tension-driven grain growth is best represented by

a (virtual) vertex model [443, 444]. In such a model the driving force is the

net grain boundary surface tension at a vertex. A vertex can be a triple junc-

tion or any point on a polygonized grain boundary. For a given time interval

the equation of motion is solved concomitantly for all vertices. Each vertex is

assigned a mobility so that diﬀerent mobilities for triple junctions and bound-

aries can easily be implemented.

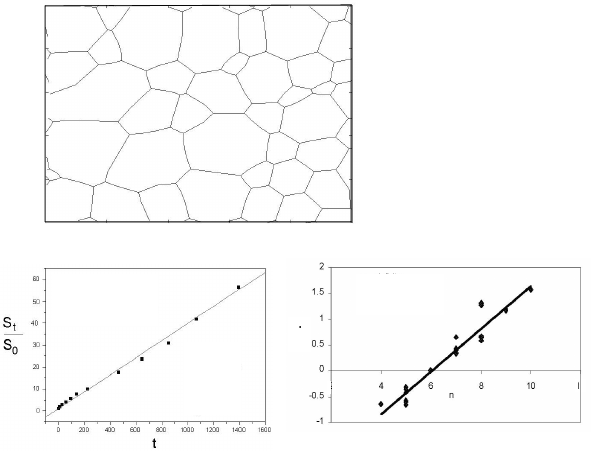
In Fig. 4.40 the simulated evolution of the microstructure of a 2D poly-

crystal is presented at various stages of grain growth. The evolution was fully

controlled by grain boundary kinetics. The time dependence of the mean grain

area was computed. As apparent from Fig. 4.40a the grains are bordered by

curved boundaries. The dependence of the mean grain area on time, and par-

ticularly the dependence of the rate of grain area change

S vs. the topological

class n of a grain are shown in Fig. 4.40b,c. They reﬂect all features that are

peculiar to a “Von Neumann-Mullins” polycrystal: <S>increases linearly

with annealing time; the rate of grain area change

S is linear in n,andthe

line

S(n) intersects the axis n at n = 6, i.e.

S =0atn =6.Theslopeof

the line

S(n)=

πm

is as predicted by the Von Neumann-Mullins relation.

A decrease in the criterion Λ increases the eﬀect of triple junctions on grain

growth.

Two essentially diﬀerent situations were considered [442]. The ﬁrst case

related to the kinetics when the triple junction inﬂuence is tangibly large,

but nevertheless, the evolution of the system can be described as a result

of curvature-driven grain boundary motion. In contrast to unconstrained

grain boundary motion, however, the boundaries are much more straight

(Fig. 4.41a). When Λ is still relatively large, 0.4 ≤ Λ ≤ 5.0, the mean grain

area <S>changes linearly with time t, which reﬂects the nature of the con-

trolling grain boundary kinetics of the system at this stage (Fig. 4.41b). The

quantitative variation of the rate of grain area change

S on topological class

n, which is a straight line for pure grain boundary kinetics (Fig. 4.40c), is

transformed to an area under the constraint of a ﬁnite triple junction mobil-

ity (Fig. 4.41c). For all topological classes a large scatter of

S(n) is observed.

While for unconstrained grain boundary kinetics (inﬁnite junction mobility)

S is a function of n only, for a system with ﬁnite junction mobility

S becomes

a function of both n and Λ,

S =

S(n, Λ) (Fig. 4.41c). The straight line in

Fig. 4.41c, which describes the Von Neumann-Mullins relationship, has the

slope

πm

and

S(n =6)=0.

As the parameter Λ decreases the inﬂuence of triple junction drag becomes

obvious not only in the

S − n diagram, but also in changes of the depen-

dency S(t) (Fig. 4.42). Hence, grain growth cannot be considered any longer

394 4 Thermodynamics and Kinetics of Connected Grain Boundaries

100

020406080100

(a)

(c)

(b)

100

020406080100

(a)

(c)

(b)

FIGURE 4.40

Simulation results for a 2D polycrystal for grain boundary kinetics (Λ →∞).

(a) Microstructure at S(t)/S

=1.72; (b) normalized area S(t)/S

vs. time t;

(c)

S as function of n.