Gottstein G., Shvindlerman L.S. Grain Boundary Migration in Metals: Thermodynamics, Kinetics, Applications

Подождите немного. Документ загружается.

4.5 Experimental Investigations of Triple Junction Motion 355

= 0.4

365 370 375 380 385 390 395 400

T [°C]

= 0.4

365 370 375 380 385 390 395 400

T [°C]

= 0.4

FIGURE 4.16

Temperature dependence of the criterion Λ for a symmetrical triple junction

(sample S2).

= 1

340

350 360 370 380 390 400 410

T [°C]

= 1

340

350 360 370 380 390 400 410

T [°C]

= 1

FIGURE 4.17

Temperature dependence of the criterion Λ for an ideal triple junction (sample

S3).

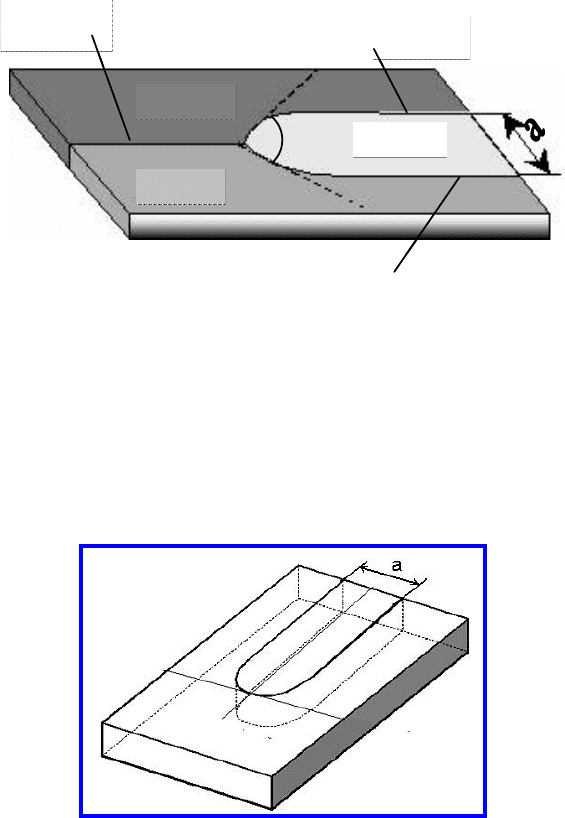
356 4 Thermodynamics and Kinetics of Connected Grain Boundaries

2θ

GB II

Grain 1

Grain 2

Grain 3

GB III

GB I

2θ

GB II

Grain 1

Grain 2

Grain 3

GB III

GB I

FIGURE 4.18

Geometry of grain boundary system with triple junction.

FIGURE 4.19

Geometry of a grain boundary half loop, i.e. the grain boundary system in

Fig. 4.18 without triple junction.

4.5 Experimental Investigations of Triple Junction Motion 357

grain boundary system (Fig. 4.18) can be applied completely to a symmetrical

system, where grain boundaries I and II are the same, but diﬀerent from the

rectilinear grain boundary III. This diﬀerence manifests itself in the relation

for the dimensionless criterion Λ and in the value of the equilibrium angle Θ

Eqs. (4.44) and (4.45). The essential issue is the problem how to determine

. In [434] this problem was treated by two methods. In the ﬁrst method

one grain boundary system was stopped by notches near the triple junction;

it gave a possibility to measure Θ

. An alternative way consists of using lit-

erature data of grain boundary surface tension in Al. In our case we used the

Read-Shockley equation to estimate the ratio between the surface tension of

low-angle and high-angle grain boundaries.

Two grain boundary systems were studied: a 11

20 tilt boundary system

with 84

◦

misorientation of the curved boundaries (half-loop); the misorienta-

tion across the straight boundary was about 3

◦

. The second grain boundary

system was a system of 10

10 tilt boundaries. The misorientation for the half-

loop was 62

◦

, the misorientation of straight boundary was also about 3

◦

.The

velocities and mobilities of the grain boundary systems for the two types of

motion were compared; i.e. in free motion — half-loop — and in constrained

motion — half-loop with triple junction. In the following the product of the

displacement of the grain boundary vertex and the width of the grain a, i.e.

a(t) will be referred to as reduced displacement.

In Fig. 4.20 the dependency of the reduced displacement a(t)ontimefora

grain boundary half-loop and a half-loop with a triple junction are presented.

Although half-loops (and half-loops with triple junction) of diﬀerent width

were studied experimentally, the comparison of the product a(t)compen-

sates the discrepancy between the major parameter of driving force — the

width a. Strictly speaking, in the driving force for the half-loop and half-loop

with triple junction would be

2γ

and

2γ

−

III

respectively, and should be

taken into consideration as well; however, since GBIII is a low-angle bound-

ary, we reason that such small correction may be disregarded. One can see,

the performed experiment brings out clearly that the triple junction strongly

drags grain boundary motion.

Let us consider the mobility of grain boundary and triple junction. Since

the exact value of γ, the grain boundary surface tension, is usually unknown it

is convenient to use the reduced mobility, A

and A

, which can be expressed,

respectively, as

= m

γ − for a half-loop (4.49)

2Θ

= m

γ − for a grain boundary system with triple junction

(4.50)

2cosΘ−

III

− for a grain boundary system with triple junction

(4.51)

358 4 Thermodynamics and Kinetics of Connected Grain Boundaries

0 50 100 150 200 250

time, sec

0.10

1.10

-07

2.10

-07

3.10

-07

4.10

-07

5.10

-07

a.l(t), m

0 50 100 150 200 250

time, sec

0.10

1.10

-07

2.10

-07

3.10

-07

4.10

-07

5.10

-07

a.l(t), m

FIGURE 4.20

Time dependence of reduced displacement a(t)for10

10 tilt grain boundary

half-loop (solid circles) and triple junction conﬁguration (solid squares) for

misorientation angle 62

◦

at T = 390

◦

C [434].

(Contrary to m

and m

, the quantities A

and A

havethesamedimen-

sion).

The temperature dependency of A

and A

for system I and II is presented

in Figs. 4.21 and 4.22. It can be seen that the dependency can be subdivided

into two regions. The ﬁrst one can be characterized by the relation A

In this region the motion of the system is controlled by the triple junction

mobility. The second region is deﬁned by the relationship A

.Inthis

region the motion of a grain boundary system is determined by the grain

boundary mobility.

In Fig. 4.21 some experimental points that reﬂect the motion of a grain

boundary system with triple junction were recalculated according to the equa-

tion for boundary kinetics (Eq. 4.50). We are dealing with the points lying

above the intersection point with the line A





— mobility of the half-loop.

One can see that the recalculated points — open circles — are in good agree-

ment with the half-loop mobility (solid circles). It should be borne in mind

that the transition temperature between these two kinetics regimes might be

higher than the melting point. In such case the motion of the grain boundary

system will be governed by the triple junction mobility in the whole temper-

ature range.

The results obtained in the experiments on Zn tricrystals [434] were quali-

tatively conﬁrmed by investigations on Al tricrystals [436], [437].

Since the mobility of grain boundaries in Al has been well investigated in

bicrystal experiments, such measurements permit a direct comparison of grain

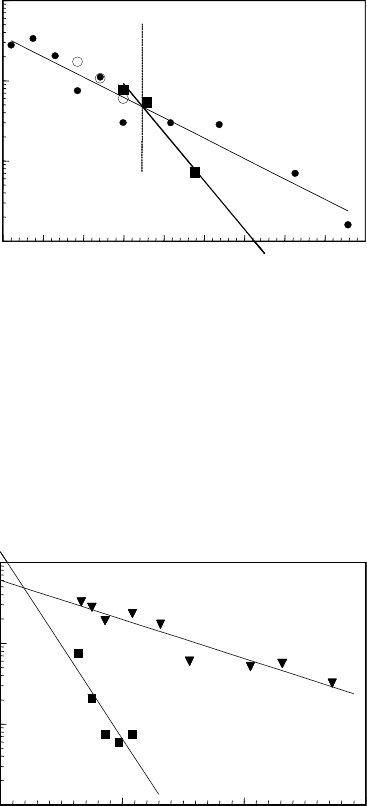
4.5 Experimental Investigations of Triple Junction Motion 359

1.46 1.48 1.5 1.52 1.54 1.56 1.58 1.6 1.62 1.64

-11

-10

-9

-8

III

/s]

()

1/T 10 / K

−

1.46 1.48 1.5 1.52 1.54 1.56 1.58 1.6 1.62 1.64

-11

-10

-9

-8

III

/s]

1.46 1.48 1.5 1.52 1.54 1.56 1.58 1.6 1.62 1.64

-11

-10

-9

-8

III

/s]

()

1/T 10 / K

−

FIGURE 4.21

Temperature dependence of reduced grain boundary mobility A

(solid cir-

cles) and reduced triple junction mobility A

(solid squares) for 10

10 tilt

boundaries in Zn; the regions I and II are the regions of grain boundary and

triple junction kinetics, respectively [434].

1.4 1.5 1.6 1.7

-11

-10

-09

-08

/s]

()

1/T 10 /K

−

1.4 1.5 1.6 1.7

-11

-10

-09

-08

/s]

1.4 1.5 1.6 1.7

-11

-10

-09

-08

/s]

()

1/T 10 /K

−

FIGURE 4.22

Temperature dependence of reduced grain boundary mobility A

(solid trian-

gles) and reduced triple junction mobility A

(solid squares) for 11

20 tilt

boundaries in Zn [434].

360 4 Thermodynamics and Kinetics of Connected Grain Boundaries

boundary and triple junction properties. The experiments were carried out on

tricrystals of high purity (99,999%) aluminium with a grain boundary geom-

etry as shown in Fig. 4.18. The crystallographic characteristics of the studied

tricrystals are given in Table 4.2. The orientations of the three contiguous

grains of each sample were determined by the Laue technique and electron

back scatter diﬀraction (EBSD).

The motion of three grain boundaries systems with triple junctions (Ta-

TABLE 4.2

Misorientation of the Investigated

Tricrystals

Sample GB I GB II GB III

SI 21

◦

111 18

◦

111 3

◦

111

SII 27

◦

110 22

◦

110 5

◦

110

S III 44

◦

110 29

◦

110 15

◦

110

ble 4.2) was investigated in the temperature range between 400 and 590

◦

[436]. The investigated triple junctions consisted of two high-angle tilt grain

boundaries (GBI and GBII) and a low-angle tilt boundary (GB III). Due to

diﬀerent properties of low-angle and high-angle grain boundaries and under

the assumption that the properties of high-angle grain boundaries vary only

little with changing misorientation, the investigated grain boundary systems

can be regarded as symmetrical junctions.

For all samples investigated the velocities V were found to remain constant

during an experiment at a given temperature over the entire investigated tem-

perature range. This supports the idea of a steady-state character of motion.

The angle Θ was seen to increase with increasing temperature (Table 4.3).

Due to the temperature dependence of Θ, the criterion Λ, determined by

Eqs (4.30) and (4.45), was found to increase with increasing temperature as

well. For a calculation of Λ for the motion of grain boundaries in sample SI

the ratio γ

III

/γ was determined under the assumption that for temperatures

near the melting point the value of Θ reaches the thermodynamic equilibrium

value

(Θ

= arccos



III

2γ



). The values of the ratio γ

III

/γ for all investi-

gated systems are given in Table 4.3.

The measured quantities in the current experiments were the migration

rate V of the grain boundary system with triple junction and the triple junc-

tion angle Θ. Using the measured values of Θ, the dimensionless parameter Λ

was calculated for each annealing temperature, and the temperature depen-

It is obvious that Θ → Θ

when the kinetics of the system become grain boundary

controlled. In other words Θ

measured

∼

can be expected near the melting point.

4.5 Experimental Investigations of Triple Junction Motion 361

TABLE 4.3

Parameters of the Motion of Investigated Grain Boundary Systems with Triple

Junctions in Al Tricrystals [436]

Sample T

◦

CΘ Λ VA

m/s m

/s m

/s eV eV

398 58.5 2.6 0.58 · 10

−6

8.7 · 10

−10

SI 418 62 3.19 1.1 · 10

−6

2.0 · 10

−9

3.2

418 62 3.19 1.17 · 10

−6

2.5 · 10

−9

= 438 67 4.5 5.52 · 10

−6

2.8 · 10

−9

1.3 · 10

−8

=0.261 454 72.5 7.4 1.47 · 10

−5

7.0 · 10

−9

5.2 · 10

−8

1.4

459 78 16.6 6.4 · 10

−6

3.4 · 10

−9

5.7 · 10

−8

479 80 32.4 1.45 · 10

−5

7.6 · 10

−9

2.5 · 10

−8

479 55 2.2 5.8 · 10

−7

6.6 · 10

−10

SII 489 61.5 3.2 1.13 · 10

−6

1.7 · 10

−9

2.7

510 61.5 3.2 4.79 · 10

−6

6.0 · 10

−9

530 62 3.3 1.85 · 10

−5

7.4 · 10

−9

= 551 63.5 3.7 3.3 · 10

−5

1.4 · 10

−8

= 0.286 571 70 6.1 4.32 · 10

−5

1.9 · 10

−8

1.4

591 72 7.4

SIII 530 61.5 9.8 5.11 · 10

−7

2.7 · 10

−9

551 62 10.9 1.0 · 10

−5

5.3 · 10

−9

= 571 64 16.4 1.86 · 10

−5

9.8 · 10

−9

= 0.735 591 67 50.7 2.06 · 10

−6

9.4 · 10

−9

dency of Λ was determined. Fig. 4.23 shows this dependency for the samples

of type SI. According from the approach outlined above, at low temperatures,

where Λ is of the order of unity, the motion of the grain boundary system

is controlled by the mobility of the triple junction. A rise of Λ with increas-

ing temperature reﬂects the transition from triple junction to grain boundary

controlled motion of the grain boundary system. The technique used for mea-

suring the angle Θ raises the important question whether the angle measured

after the sample was cooled down corresponded to the real triple junction

angle at annealing temperature. There are two main factors, which may af-

fect the angle Θ: a thermodynamical inﬂuence, which reﬂects the temperature

dependence of the grain boundary surface tension, and a kinetic inﬂuence, de-

ﬁned by the relation between grain boundary and triple junction mobilities

and the width of the vanishing grain a. The thermodynamical eﬀect is negligi-

ble, since the boundary surface tension depends only slightly on temperature,

although how slightly is not exactly known. In any event, if the grain bound-

ary surface tensions and their temperature coeﬃcients are comparable, then

the angle Θ should be essentially temperature independent. The kinetic factor

can really aﬀect the magnitude of the angle Θ. Taking into account that triple

junction kinetics predominate at relatively low temperatures [436, 437], the

observed value of Θ may be reduced compared to the real angle at annealing

temperature. However, due to the strong temperature dependence of grain

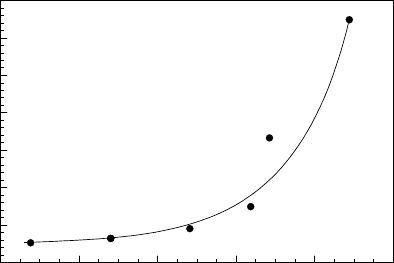
362 4 Thermodynamics and Kinetics of Connected Grain Boundaries

390 410 430 450 470 490

T [°C]

FIGURE 4.23

Temperature dependence of the criterion Λ for triple junctions in Al [436].

boundary mobility and the high cooling rate of the sample this change in the

real value of Θ is likely to be suﬃciently small.

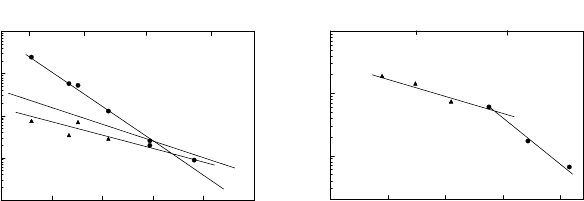
The reduced mobilities for grain boundaries and triple junctions are given

in Fig. 4.24 where the triangles represent the (reduced) grain boundary mo-

bility, whereas the circles denote the respective triple junction mobility. The

system is obviously controlled by the slowest moving constituent, i.e. the triple

junction at low temperatures and the grain boundary at high temperatures.

According to their respective linear behavior in the Arrhenius plot the activa-

tion enthalpy can be determined as indicated in the ﬁgure. Obviously, there

is a distinct transition from triple junction kinetics at low temperatures to

grain boundary kinetics at elevated temperatures, and the activation enthalpy

for triple junction motion H

is considerably higher than for grain bound-

ary migration (H

). The behavior of the grain-boundary-controlled branch in

Fig. 4.24 compares well with measurements of the reduced grain boundary

mobility obtained from the data (see Chapter 3) of independent bicrystal ex-

periments. The corresponding evaluation for system SI is given in Fig. 4.24(a)

and yields comparable behavior.

We would like to stress two points. First, there is a transition tempera-

ture between two kinetic regimes, namely between grain boundary and junc-

tion regime. This transition temperature between these two kinetics regimes

might be either higher than the melting point, or a rather low temperature, in

particular lower than the temperature range of measurements. In this latter

case the motion of a grain boundary system will be governed by the grain

boundary mobility in the whole temperature range. One example is given in

Fig. 4.25. The measurements of grain boundary motion in the sample SIII

4.5 Experimental Investigations of Triple Junction Motion 363

1.3 1.35 1.4 1.45 1.5 1.55

1/T [10

/K]

-10

-9

-8

-7

-6

[

]

T°C

390

450

420

480

H=3.2 eV

H=1.4 eV

1.14 1.19 1.24 1.29 1.34

1/T [10

/K]

-9

-8

-7

[

]

500

T°C

550

H=1.4 eV

H=2.7 eV

(a)

(b)

1.3 1.35 1.4 1.45 1.5 1.55

1/T [10

/K]

-10

-9

-8

-7

-6

[

]

T°C

390

450

420

480

H=3.2 eV

H=1.4 eV

1.14 1.19 1.24 1.29 1.34

1/T [10

/K]

-9

-8

-7

[

]

500

T°C

550

H=1.4 eV

H=2.7 eV

(a)

(b)

FIGURE 4.24

Temperature dependence of triple junction (• ) and grain boundary mobility

() in samples SI (a) and SII (b). Dotted line represents the mobility of

a21

◦

111 tilt boundary in Al as reconstructed from literature data (see

Chapter 3) (H =1.6eV; A

=10

/s) [436].

were performed at a relatively high temperature. The persistently higher val-

ues of Λ and the constant but comparatively low activation enthalpy in the

entire investigated temperature range (Fig. 4.25) indicate that the system

always moves in the boundary-controlled regime. Obviously, this has to be

attributed to the structure and property of the rectilinear grain boundary in

sample SIII which is practically a high-angle boundary contrary to the respec-

tive boundaries in the samples SI and SII, which are low-angle boundaries.

It is noteworthy that the motion of system SII, also consisting of 110 tilt

boundaries, in this temperature range is controlled by boundary motion as

well.

Further, we would like to draw the attention of the reader to the essen-

tial diﬀerence in the activation enthalpy of grain boundary and triple junc-

tion motion. The activation enthalpy of triple junction motion is much larger

than the respective quantity for grain boundaries. However, these data are

not enough to determine the kinetic regime which controls the motion of the

grain boundary system with a junction. The explanation for this phenomenon

can be provided on the basis of the compensation eﬀect. The compensation

eﬀect manifests itself in a linear dependence between the logarithm of the

pre-exponential factor and the enthalpy of activation in the mobility relation.

A comprehensive description of this eﬀect is given in Chapter 3. It was shown

that the compensation eﬀect can be derived in the framework of a ﬁrst-order

phase transition between the equilibrium state and the metastable “activation

barrier” state. The temperature and pressure of compensation correspond to

the temperature and the pressure of equilibrium between the “barrier” and

ground state. Experimental data indicate also that the compensation tem-

perature is often close to the equilibrium temperature of a ﬁrst-order phase

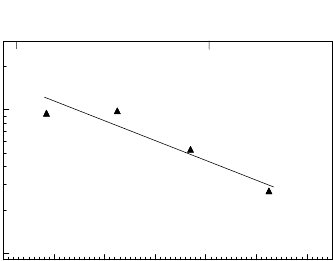
364 4 Thermodynamics and Kinetics of Connected Grain Boundaries

1.14 1.16 1.18 1.2 1.22 1.24 1.26

1/T [10

/K]

-9

-8

[

]

550

600

T [°C]

H=1.3 eV

FIGURE 4.25

Temperature dependence of the reduced mobility of grain boundaries in sam-

ple SIII [436].

transformation in the bulk. As has been shown, the compensation eﬀect rather

than the energy of activation or the pre-exponential factor individually con-

trols the kinetics of thermally activated interfacial processes. The results of

[437] where the motion of a rather large number of grain boundary systems

with triple junction in specially grown Al tricrystals was studied are very

useful to analyze this phenomenon. The crystallography and the kinetic pa-

rameters of grain boundaries and triple junctions investigated in [437] are

presented in Table 4.4. (Table 4.4 includes also some data listed in Table 4.2.)

Fig. 4.26 demonstrates the compensation eﬀect for the mobility of grain

boundary systems with triple junction and individual tilt grain boundaries in

Al.

It is of interest to compare the transition temperature from triple junction

kinetics to grain boundary kinetics with the compensation temperature (Table

4.5). Apparently, the kinetic transition temperature compares to the compen-

sation temperature for all grain boundary systems with triple junctions, i.e.

is in accordance with the concept put forward in Sec. 3.7: the compensation

temperature is the equilibrium temperature between ground state and acti-

vated state. As shown in Sec. 3.7, this concept is supported by numerous

observations that the compensation temperature is close to the temperature

of a nearby phase transition. From the experimental data discussed above it

transpires that for the motion of a grain boundary system with triple junction

the compensation temperature coincides with the temperature of the kinetic

phase transition from the grain boundary regime to the junction regime.

In other words, the compensation temperature is the border between two

kinetic regimes: grain boundary kinetics and triple junction kinetics. Below